2020-2021学年苏科版七年级数学下册7.4节认识三角形同步练习(Word版,附答案)
文档属性
| 名称 | 2020-2021学年苏科版七年级数学下册7.4节认识三角形同步练习(Word版,附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 141.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-25 00:00:00 | ||
图片预览



文档简介
苏科版初中数学七年级下册第七章平面图形的认识(二)7.4节认识三角形同步练习
一、单选题
1.下列长度的三条线段能组成三角形的是(???
)
A.?1,2,3??????????????????????????B.?4,5,10??????????????????????????C.?8,15,20??????????????????????????D.?5,8,15
2.如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且S△ABC=4cm2
,
则S阴影等于…(????
)
A.?2cm2?????????????????????????????????B.?1cm2?????????????????????????????????C.?
cm2?????????????????????????????????D.?
cm2
3.如图所示的图形中,
于
,线段AE是几个三角形的高(???
).
A.?3???????????????????????????????????????????B.?4???????????????????????????????????????????C.?5???????????????????????????????????????????D.?6
4.如图所示,为估计池塘两岸A
,
B间的距离,一位同学在池塘一侧选取了一点P
,
测得PA=16m
,
PB=12m
,
那么A
,
B间的距离不可能是( )
A.?15m????????????????????????????????????B.?18m????????????????????????????????????C.?26m????????????????????????????????????D.?30m
5.如图,在
中,BC边上的高为(????
)
A.?AB????????????????????????????????????????B.?BD????????????????????????????????????????C.?AE????????????????????????????????????????D.?BE
6.如图,已知
,则
一定是
的(??
)
A.?角平分线????????????????????????????????B.?高线????????????????????????????????C.?中线????????????????????????????????D.?无法确定
7.用三角板作
的边BC上的高,下列三角板的摆放位置正确的是(??
)
A.?B.?C.?D.?
8.三角形的两边长分别为
和
,则周长
的范围是(??
)
A.??????????????????????B.??????????????????????C.??????????????????????D.?
9.已知AD是△ABC的中线,BE是△ABD的中线,若△ACD的面积为20,则△ABE的面积为(?
???).
A.?5?????????????????????????????????????????B.?10?????????????????????????????????????????C.?15?????????????????????????????????????????D.?18
10.如图,D,E分别是△ABC的边AB、BC上的点,AD=2BD,BE=CE,设△ADF的面积为S1
,
△CEF的面积为S2
,
若S△ABC=12,则S1﹣S2=(??
)
A.?1.5??????????????????????????????????????????B.?2??????????????????????????????????????????C.?3??????????????????????????????????????????D.?0.5
11.如图,在
中,AC边上的高是(??????
)
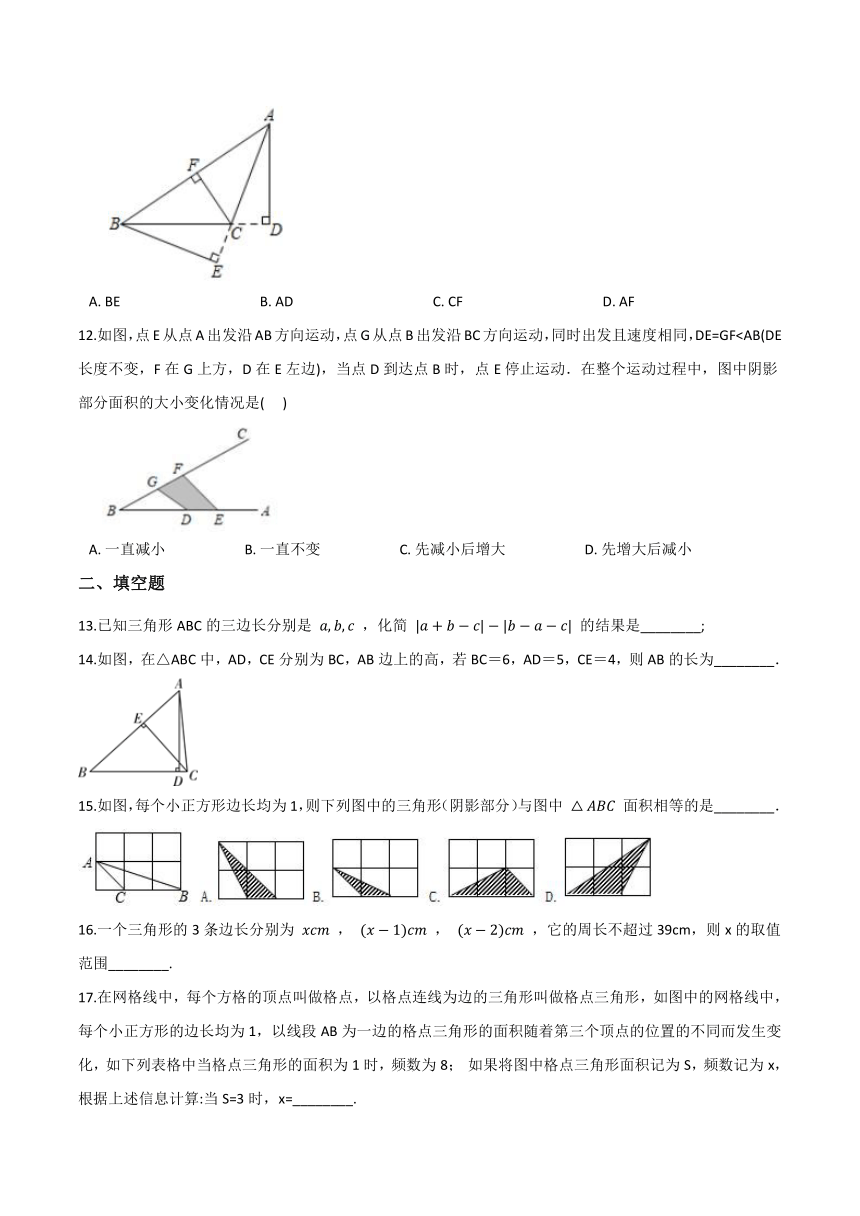
A.?BE????????????????????????????????????????B.?AD????????????????????????????????????????C.?CF????????????????????????????????????????D.?AF
12.如图,点E从点A出发沿AB方向运动,点G从点B出发沿BC方向运动,同时出发且速度相同,DE=GF)
A.?一直减小???????????????????????B.?一直不变???????????????????????C.?先减小后增大???????????????????????D.?先增大后减小
二、填空题
13.已知三角形ABC的三边长分别是
,化简
的结果是________;
14.如图,在△ABC中,AD,CE分别为BC,AB边上的高,若BC=6,AD=5,CE=4,则AB的长为________.
15.如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与图中
面积相等的是________.
16.一个三角形的3条边长分别为
,
,
,它的周长不超过39cm,则x的取值范围________.
17.在网格线中,每个方格的顶点叫做格点,以格点连线为边的三角形叫做格点三角形,如图中的网格线中,每个小正方形的边长均为1,以线段AB为一边的格点三角形的面积随着第三个顶点的位置的不同而发生变化,如下列表格中当格点三角形的面积为1时,频数为8;
如果将图中格点三角形面积记为S,频数记为x,根据上述信息计算:当S=3时,x=________.
18.如图,在
中,
,将
平移5个单位长度得到
1,点P、Q分别是
、
的中点,
的最小值等于________.
三、解答题
19.如图所示,在形状为平行四边形的一块地ABCD中,有一条小折路EFG.现在想把它改为经过点G的直路,要求小路两侧土地的面积都不变,请在图中画出改动后的小路.
20.如图,P为△ABC中任意一点.延长AP、BP、CP分别交BC、AC、AB于D、E、F.求证:AD+BE+CF>
(AB+BC+CA).
21.如图,图中A、B、C、D四点是某厂的四个生产车间,现在要厂里建一个仓库,使仓库到A、B、c、D四个生产车间的距离的和最小.问仓库应建在何处?
22.阅读理解:运用“同一图形的面积相等”可以证明一些含有线段的等式成立,这种解决问题的方法我们称之为面积法.如图1,在等腰△ABC中,AB=AC,AC边上的高为h,点M为底边BC上的任意一点,点M到腰AB、AC的距离分别为h1、h2
,
连接AM,利用S△ABC=S△ABM+S△ACM
,
可以得出结论:h=h1+h2
.
类比探究:在图1中,当点M在BC的延长线上时,猜想h、h1、h2之间的数量关系并证明你的结论.
拓展应用:如图2,在平面直角坐标系中,有两条直线l1:y=
x+3,l2:y=﹣3x+3,
若l2上一点M到l1的距离是1,试运用“阅读理解”和“类比探究”中获得的结论,求出点M的坐标.
参考答案
1.
C
2.
B
3.
D
4.
D
5.
C
6.
C
7.
A
8.
D
9.
B
10.
B
11.
A
12.
B
13.
2b-2c
14.
15.
A
16.
3<x≤14
17.
4
18.
19.
证明:设GN交FE于点I.
∵EG∥FN,∴△GNF的面积等于△EFN的面积,(同底等高).
把两个三角形面积都减去△FIN面积,所以△EIN面积等于△GIF面积,即小路两侧土地面积都不变.
20.
证明:∵在△APF中,AP+PF>AF,
在△BPF中,PF+BP>BF,
在△BPD中,BP+PD>BD,
在△CPD中,PD+PC>CD,
在△CPE中,PC+PE>CE,
在△APE中,PE+AP>AE,
∴AP+PF+PF+BP+BP+PD+PD+PC+PC+PE+PE+AP>AF+BF+BD+CD+CE+AE,
2AP+2PF+2BP+2PD+2PC+2PE>AB+BC+CA,
2(AD+BE+CF)>AB+BC+CA,
∴AD+BE+CF>""(AB+BC+CA).
21.解:如图,仓库应建在对角线AD与BC的交点P处.下面证明PA+PB+PC+PD是最小的.
设点
P′
异于P点,要证明,
PA+PB+PC+PD<
P′A+
P′B+
P′C+
P′D,
在△
P′
BC中,BC<
P′C+
P′B,即
PB+PC<
P′C+
P′B.
在△
P′AD中,AD<
P′A+
P′D,即
PA+PD<
P′A+
P′D.
相加得,
PA+PB+PC+PD<
P′
A+
P′B+
P′C+
P′D.
所以P点是所求的点.
22.解:类比探究:
结论:h=h1﹣h2
.
理由:
∵S△ABC=
AC?BD=
AC?h,
S△ABM=
AB?ME=
AB?h1
,
S△ACM=
AC?MF=
AC?h2
,
.
又∵S△ABC=S△ABM﹣S△ACM
,
∴
AC?h=
AB?h1﹣
AC?h2
.
∵AB=AC,
∴h=h1﹣h2
.
拓展应用:在y=
x+3中,令x=0得y=3;令y=0得x=﹣4,
则:A(﹣4,0),B(0,3),同理求得C(1,0),
OA=4,OB=3,AC=5,
AB=
=5,
所以AB=AC,
即△ABC为等腰三角形.
设点M的坐标为(x,y),
①当点M在BC边上时,由h1+h2=h得:
OB=1+y,y=3﹣1=2,把它代入y=﹣3x+3中求得:x=
,
∴M(
,2);
②当点M在CB延长线上时,由h1﹣h2=h得:
OB=y﹣1,y=3+1=4,把它代入y=﹣3x+3中求得:x=﹣
,
∴M(﹣
,4).
综上所述点M的坐标为(
,2)或(﹣
,4).
一、单选题
1.下列长度的三条线段能组成三角形的是(???
)
A.?1,2,3??????????????????????????B.?4,5,10??????????????????????????C.?8,15,20??????????????????????????D.?5,8,15
2.如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且S△ABC=4cm2
,
则S阴影等于…(????
)
A.?2cm2?????????????????????????????????B.?1cm2?????????????????????????????????C.?
cm2?????????????????????????????????D.?
cm2
3.如图所示的图形中,
于
,线段AE是几个三角形的高(???
).
A.?3???????????????????????????????????????????B.?4???????????????????????????????????????????C.?5???????????????????????????????????????????D.?6
4.如图所示,为估计池塘两岸A
,
B间的距离,一位同学在池塘一侧选取了一点P
,
测得PA=16m
,
PB=12m
,
那么A
,
B间的距离不可能是( )
A.?15m????????????????????????????????????B.?18m????????????????????????????????????C.?26m????????????????????????????????????D.?30m
5.如图,在
中,BC边上的高为(????
)
A.?AB????????????????????????????????????????B.?BD????????????????????????????????????????C.?AE????????????????????????????????????????D.?BE
6.如图,已知
,则
一定是
的(??
)
A.?角平分线????????????????????????????????B.?高线????????????????????????????????C.?中线????????????????????????????????D.?无法确定
7.用三角板作
的边BC上的高,下列三角板的摆放位置正确的是(??
)
A.?B.?C.?D.?
8.三角形的两边长分别为
和
,则周长
的范围是(??
)
A.??????????????????????B.??????????????????????C.??????????????????????D.?
9.已知AD是△ABC的中线,BE是△ABD的中线,若△ACD的面积为20,则△ABE的面积为(?
???).
A.?5?????????????????????????????????????????B.?10?????????????????????????????????????????C.?15?????????????????????????????????????????D.?18
10.如图,D,E分别是△ABC的边AB、BC上的点,AD=2BD,BE=CE,设△ADF的面积为S1
,
△CEF的面积为S2
,
若S△ABC=12,则S1﹣S2=(??
)
A.?1.5??????????????????????????????????????????B.?2??????????????????????????????????????????C.?3??????????????????????????????????????????D.?0.5
11.如图,在
中,AC边上的高是(??????
)
A.?BE????????????????????????????????????????B.?AD????????????????????????????????????????C.?CF????????????????????????????????????????D.?AF
12.如图,点E从点A出发沿AB方向运动,点G从点B出发沿BC方向运动,同时出发且速度相同,DE=GF
A.?一直减小???????????????????????B.?一直不变???????????????????????C.?先减小后增大???????????????????????D.?先增大后减小
二、填空题
13.已知三角形ABC的三边长分别是
,化简
的结果是________;
14.如图,在△ABC中,AD,CE分别为BC,AB边上的高,若BC=6,AD=5,CE=4,则AB的长为________.
15.如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与图中
面积相等的是________.
16.一个三角形的3条边长分别为
,
,
,它的周长不超过39cm,则x的取值范围________.
17.在网格线中,每个方格的顶点叫做格点,以格点连线为边的三角形叫做格点三角形,如图中的网格线中,每个小正方形的边长均为1,以线段AB为一边的格点三角形的面积随着第三个顶点的位置的不同而发生变化,如下列表格中当格点三角形的面积为1时,频数为8;
如果将图中格点三角形面积记为S,频数记为x,根据上述信息计算:当S=3时,x=________.
18.如图,在
中,
,将
平移5个单位长度得到
1,点P、Q分别是
、
的中点,
的最小值等于________.
三、解答题
19.如图所示,在形状为平行四边形的一块地ABCD中,有一条小折路EFG.现在想把它改为经过点G的直路,要求小路两侧土地的面积都不变,请在图中画出改动后的小路.
20.如图,P为△ABC中任意一点.延长AP、BP、CP分别交BC、AC、AB于D、E、F.求证:AD+BE+CF>
(AB+BC+CA).
21.如图,图中A、B、C、D四点是某厂的四个生产车间,现在要厂里建一个仓库,使仓库到A、B、c、D四个生产车间的距离的和最小.问仓库应建在何处?
22.阅读理解:运用“同一图形的面积相等”可以证明一些含有线段的等式成立,这种解决问题的方法我们称之为面积法.如图1,在等腰△ABC中,AB=AC,AC边上的高为h,点M为底边BC上的任意一点,点M到腰AB、AC的距离分别为h1、h2
,
连接AM,利用S△ABC=S△ABM+S△ACM
,
可以得出结论:h=h1+h2
.
类比探究:在图1中,当点M在BC的延长线上时,猜想h、h1、h2之间的数量关系并证明你的结论.
拓展应用:如图2,在平面直角坐标系中,有两条直线l1:y=
x+3,l2:y=﹣3x+3,
若l2上一点M到l1的距离是1,试运用“阅读理解”和“类比探究”中获得的结论,求出点M的坐标.
参考答案
1.
C
2.
B
3.
D
4.
D
5.
C
6.
C
7.
A
8.
D
9.
B
10.
B
11.
A
12.
B
13.
2b-2c
14.
15.
A
16.
3<x≤14
17.
4
18.
19.
证明:设GN交FE于点I.
∵EG∥FN,∴△GNF的面积等于△EFN的面积,(同底等高).
把两个三角形面积都减去△FIN面积,所以△EIN面积等于△GIF面积,即小路两侧土地面积都不变.
20.
证明:∵在△APF中,AP+PF>AF,
在△BPF中,PF+BP>BF,
在△BPD中,BP+PD>BD,
在△CPD中,PD+PC>CD,
在△CPE中,PC+PE>CE,
在△APE中,PE+AP>AE,
∴AP+PF+PF+BP+BP+PD+PD+PC+PC+PE+PE+AP>AF+BF+BD+CD+CE+AE,
2AP+2PF+2BP+2PD+2PC+2PE>AB+BC+CA,
2(AD+BE+CF)>AB+BC+CA,
∴AD+BE+CF>""(AB+BC+CA).
21.解:如图,仓库应建在对角线AD与BC的交点P处.下面证明PA+PB+PC+PD是最小的.
设点
P′
异于P点,要证明,
PA+PB+PC+PD<
P′A+
P′B+
P′C+
P′D,
在△
P′
BC中,BC<
P′C+
P′B,即
PB+PC<
P′C+
P′B.
在△
P′AD中,AD<
P′A+
P′D,即
PA+PD<
P′A+
P′D.
相加得,
PA+PB+PC+PD<
P′
A+
P′B+
P′C+
P′D.
所以P点是所求的点.
22.解:类比探究:
结论:h=h1﹣h2
.
理由:
∵S△ABC=
AC?BD=
AC?h,
S△ABM=
AB?ME=
AB?h1
,
S△ACM=
AC?MF=
AC?h2
,
.
又∵S△ABC=S△ABM﹣S△ACM
,
∴
AC?h=
AB?h1﹣
AC?h2
.
∵AB=AC,
∴h=h1﹣h2
.
拓展应用:在y=
x+3中,令x=0得y=3;令y=0得x=﹣4,
则:A(﹣4,0),B(0,3),同理求得C(1,0),
OA=4,OB=3,AC=5,
AB=
=5,
所以AB=AC,
即△ABC为等腰三角形.
设点M的坐标为(x,y),
①当点M在BC边上时,由h1+h2=h得:
OB=1+y,y=3﹣1=2,把它代入y=﹣3x+3中求得:x=
,
∴M(
,2);
②当点M在CB延长线上时,由h1﹣h2=h得:
OB=y﹣1,y=3+1=4,把它代入y=﹣3x+3中求得:x=﹣
,
∴M(﹣
,4).
综上所述点M的坐标为(
,2)或(﹣
,4).
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
