2020-2021学年苏科版七年级数学下册7.5节多边形的内角与外角和同步练习(Word版,附答案)
文档属性
| 名称 | 2020-2021学年苏科版七年级数学下册7.5节多边形的内角与外角和同步练习(Word版,附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 185.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-25 00:00:00 | ||
图片预览



文档简介
苏科版初中数学七年级下册第七章平面图形的认识(二)7.5节多边形的内角与外角和同步练习
一、单选题
1.一个n边形的每一个外角都是72°,则n等于( )
A.?3???????????????????????????????????????????B.?4???????????????????????????????????????????C.?5???????????????????????????????????????????D.?6
2.从八边形的一个顶点引对角线,最多把它分割成三角形的个数为(??
)
A.?5???????????????????????????????????????????B.?6???????????????????????????????????????????C.?7???????????????????????????????????????????D.?8
3.一个三角形三个内角的度数之比为3:4:5,这个三角形一定是(??
)
A.?锐角三角形???????????????????????B.?直角三角形???????????????????????C.?钝角三角形???????????????????????D.?等腰三角形
4.将一副三角板按如图所示的方式放置,若
,则
的度数为(??
)
A.?95°?????????????????????????????????????B.?85°?????????????????????????????????????C.?105速?????????????????????????????????????D.?80°
5.将一副三角尺按如图所示的方式摆放,则
的大小为(??
)
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
6.如图,∠ACD是
ABC的一个外角,CE平分∠ACD,F为CA延长线上的一点,FG
CE,交AB于点G,若∠1=70°,∠2=36°,则∠3=(??
)
A.?36°???????????????????????????????????????B.?40°???????????????????????????????????????C.?34°???????????????????????????????????????D.?70°
7.如图,小明从点A出发沿直线前进10米到达点B,向左转
后又沿直线前进10米到达点C,再向左转
后沿直线前进10米到达点D……照这样走下去,小明第一次回到出发点A时所走的路程为(??
)
A.?100米???????????????????????????????????B.?80米???????????????????????????????????C.?60米???????????????????????????????????D.?40米
8.如图所示,光线L照射到平面镜I上,然后在平面镜Ⅰ、Ⅱ之间来回反射,已知∠α=55°,∠γ=75°,则∠β为(??
)
A.?50°???????????????????????????????????????B.?55°???????????????????????????????????????C.?60°???????????????????????????????????????D.?65°
9.n边形所有对角线的条数有(??
)
A.?
条?????????????????????????B.?
条?????????????????????????C.?
条?????????????????????????D.?
条
10.如图,∠A+∠B
+∠C
+∠D
+∠E等于( )
A.?180°????????????????????????????????????B.?360°????????????????????????????????????C.?540°????????????????????????????????????D.?720°
11.如图,五边形
中,
.若
,则
的度数为(??
)
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
12.已知Rt△ABC的三边分别为a、b、c,则下列结论不可能成立的是( )
A.?a2﹣b2=c2?????????B.?∠A﹣∠B=∠C?????????C.?∠A:∠B:∠C=3:4:5?????????D.?a:b:c=7:24:25
二、填空题
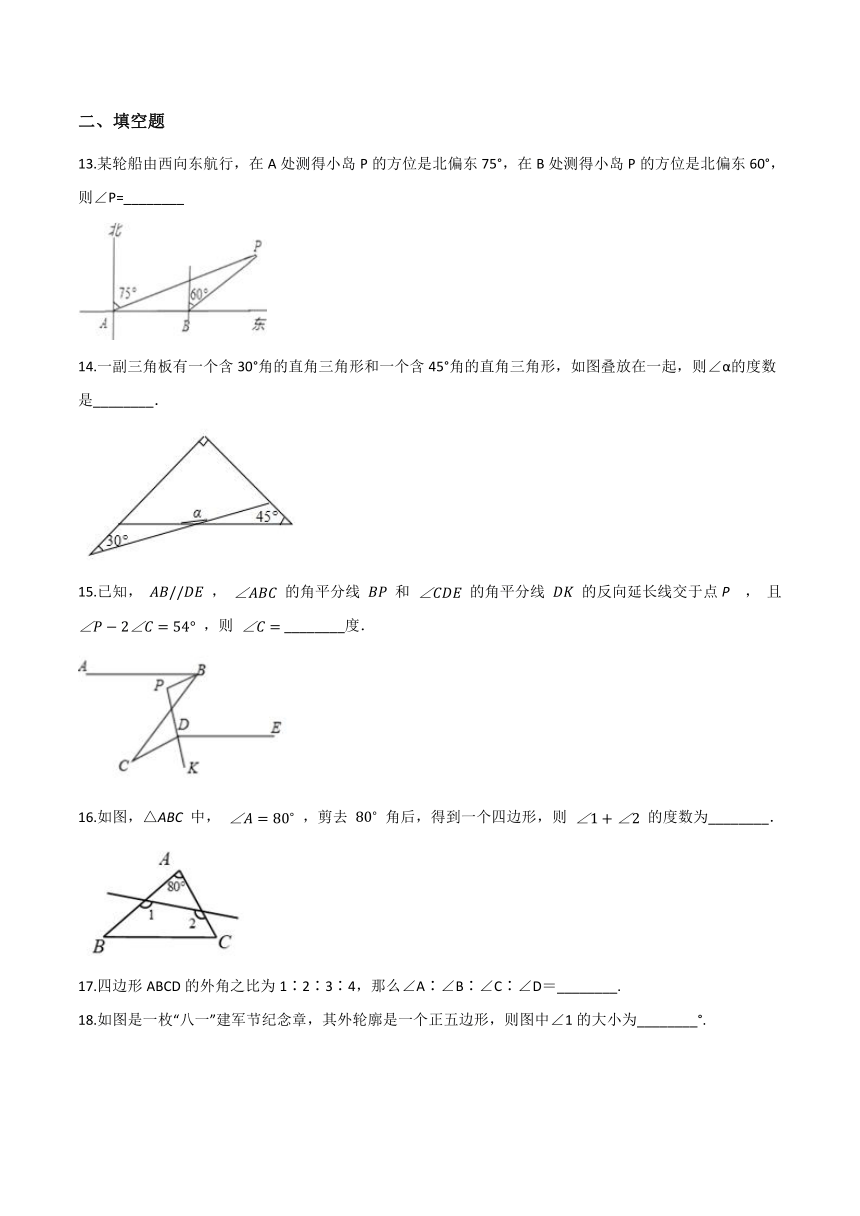
13.某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,在B处测得小岛P的方位是北偏东60°,则∠P=________
14.一副三角板有一个含30°角的直角三角形和一个含45°角的直角三角形,如图叠放在一起,则∠α的度数是________.
15.已知,
,
的角平分线
和
的角平分线
的反向延长线交于点P
,
且
,则
________度.
16.如图,△ABC
中,
,剪去
角后,得到一个四边形,则
的度数为________.
17.四边形ABCD的外角之比为1∶2∶3∶4,那么∠A∶∠B∶∠C∶∠D=________.
18.如图是一枚“八一”建军节纪念章,其外轮廓是一个正五边形,则图中∠1的大小为________°.
三、解答题
19.如图是一个凹多边形,
,
,
,
;求
的值.
20.如图,AB∥CD,∠ABE=60°,∠D=50°,求∠E的度数.
21.用两种方法证明“三角形的一个外角等于其不相邻的两个内角之和”.如图,∠DAB是△ABC的一个外角.求证:∠DAB=∠B+∠C.
证法1:∵∠BAC+∠B+∠C=180°(??
)
∠BAC+∠DAB=180°(平角的定义)
∴∠BAC+∠B+∠C=∠BAC+∠DAB(??
)
∴∠DAB=∠B+∠C(??
)
请把证法1依据填充完整,并用不同的方法完成证法2.
22.??????????????????????????
(1)已知直线AB∥CD,点P为平行线AB,CD之间的一点.如图1,若∠ABP=50°,∠CDP=60°,BE平分∠ABP,DE平分∠CDP,求∠BED的度数.
(2)(探究)如图2,当点P在直线AB的上方时,若∠ABP=α,∠CDP=β,∠ABP和∠CDP的平分线交于点E1
,
∠ABE1与∠CDE1的角平分线交于点E2
,
∠ABE2与∠CDE2的角平分线交于点E3
,
…以此类推,求∠En的度数.
(3)(变式)如图3,∠ABP的角平分线的反向延长线和∠CDP的补角的角平分线交于点E,试猜想∠P与∠E的数量关系,并说明理由.
参考答案
1.
C
2.
B
3.
A
4.
A
5.
B
6.
C
7.
B
8.
D
9.
C
10.
A
11.
C
12.
C
13.
15°
14.
165°
15.
24
16.
260°
17.
4:3:2:1
18.
108
19.
证明:连接
∵
,
∴
?,
∵
,
,
,
,
∴
.
20.
解:因为AB∥CD,
所以∠CFE=∠ABE=60°.
因为∠D=50°,
所以∠E=∠CFE-∠D=60°-50°=10°.
21.
解:证法1:∵∠BAC+∠B+∠C=180°(三角形内角和定理),
∠BAC+∠DAB=180°(平角的定义),
∴∠BAC+∠B+∠C=∠BAC+∠DAB(等量代换),
∴∠DAB=∠B+∠C(等式性质);
证法2:过A点作AE∥BC,
∵AE∥BC,
∴∠DAE=∠C,
∠EAB=∠B,
又∵∠DAB=∠DAE+∠EAB,
∴∠DAB=∠B+∠C.
22.
(1)解:如图1,过E作EF∥AB,而AB∥CD,
∴AB∥CD∥EF,
∴∠ABE=∠FEB,∠CDE=∠FED,
∴∠BED=∠BEF+∠DEF=∠ABE+∠CDE,
又∵∠ABP=50°,∠CDP=60°,BE平分∠ABP,DE平分∠CDP,
∴∠ABE=
∠ABP=25°,∠CDE=
∠CDP=30°,
∴∠BED=25°+30°=55°,
故答案为55°;
(2)如图2,∵∠ABP和∠CDP的平分线交于点E1
,
∴∠ABE1=
∠ABP=
α,∠CDE1=
∠CDP=
,
∵AB∥CD,
∴∠CDF=∠AFE1=
,
∴∠E1=∠AFE1﹣∠ABE1=
﹣
α=
(β﹣α),
∵∠ABE1与∠CDE1的角平分线交于点E2
,
∴∠ABE2=
∠ABE1=
α,∠CDE2=
∠CDE1=
,
∵AB∥CD,
∴∠CDG=∠AGE2=
,
∴∠E2=∠AGE2﹣∠ABE2=
(β﹣α),
同理可得,∠E3=
(β﹣α),
以此类推,∠En的度数为
(β﹣α).
(3)∠DEB=90°﹣
∠P.理由如下:
如图3,过E作EG∥AB,而AB∥CD,
∴AB∥CD∥EG,
∴∠MBE=∠BEG,∠FDE=∠GED,
∴∠DEB=∠BEG+∠DEG=∠MBE+∠FDE=∠ABQ+∠FDE,
又∵∠ABP的角平分线的反向延长线和∠CDP的补角的角平分线交于点E,
∴∠FDE=
∠PDF=
(180°﹣∠CDP),∠ABQ=
∠ABP,
∴∠DEB=
∠ABP+
(180°﹣∠CDP)=90°﹣
(∠CDP﹣∠ABP),
∵AB∥CD,
∴∠CDP=∠AHP,
∴∠DEB=90°﹣
(∠CDP﹣∠ABP)=90°﹣
(∠AHP﹣∠ABP)=90°﹣
∠P.
一、单选题
1.一个n边形的每一个外角都是72°,则n等于( )
A.?3???????????????????????????????????????????B.?4???????????????????????????????????????????C.?5???????????????????????????????????????????D.?6
2.从八边形的一个顶点引对角线,最多把它分割成三角形的个数为(??
)
A.?5???????????????????????????????????????????B.?6???????????????????????????????????????????C.?7???????????????????????????????????????????D.?8
3.一个三角形三个内角的度数之比为3:4:5,这个三角形一定是(??
)
A.?锐角三角形???????????????????????B.?直角三角形???????????????????????C.?钝角三角形???????????????????????D.?等腰三角形
4.将一副三角板按如图所示的方式放置,若
,则
的度数为(??
)
A.?95°?????????????????????????????????????B.?85°?????????????????????????????????????C.?105速?????????????????????????????????????D.?80°
5.将一副三角尺按如图所示的方式摆放,则
的大小为(??
)
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
6.如图,∠ACD是
ABC的一个外角,CE平分∠ACD,F为CA延长线上的一点,FG
CE,交AB于点G,若∠1=70°,∠2=36°,则∠3=(??
)
A.?36°???????????????????????????????????????B.?40°???????????????????????????????????????C.?34°???????????????????????????????????????D.?70°
7.如图,小明从点A出发沿直线前进10米到达点B,向左转
后又沿直线前进10米到达点C,再向左转
后沿直线前进10米到达点D……照这样走下去,小明第一次回到出发点A时所走的路程为(??
)
A.?100米???????????????????????????????????B.?80米???????????????????????????????????C.?60米???????????????????????????????????D.?40米
8.如图所示,光线L照射到平面镜I上,然后在平面镜Ⅰ、Ⅱ之间来回反射,已知∠α=55°,∠γ=75°,则∠β为(??
)
A.?50°???????????????????????????????????????B.?55°???????????????????????????????????????C.?60°???????????????????????????????????????D.?65°
9.n边形所有对角线的条数有(??
)
A.?
条?????????????????????????B.?
条?????????????????????????C.?
条?????????????????????????D.?
条
10.如图,∠A+∠B
+∠C
+∠D
+∠E等于( )
A.?180°????????????????????????????????????B.?360°????????????????????????????????????C.?540°????????????????????????????????????D.?720°
11.如图,五边形
中,
.若
,则
的度数为(??
)
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
12.已知Rt△ABC的三边分别为a、b、c,则下列结论不可能成立的是( )
A.?a2﹣b2=c2?????????B.?∠A﹣∠B=∠C?????????C.?∠A:∠B:∠C=3:4:5?????????D.?a:b:c=7:24:25
二、填空题
13.某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,在B处测得小岛P的方位是北偏东60°,则∠P=________
14.一副三角板有一个含30°角的直角三角形和一个含45°角的直角三角形,如图叠放在一起,则∠α的度数是________.
15.已知,
,
的角平分线
和
的角平分线
的反向延长线交于点P
,
且
,则
________度.
16.如图,△ABC
中,
,剪去
角后,得到一个四边形,则
的度数为________.
17.四边形ABCD的外角之比为1∶2∶3∶4,那么∠A∶∠B∶∠C∶∠D=________.
18.如图是一枚“八一”建军节纪念章,其外轮廓是一个正五边形,则图中∠1的大小为________°.
三、解答题
19.如图是一个凹多边形,
,
,
,
;求
的值.
20.如图,AB∥CD,∠ABE=60°,∠D=50°,求∠E的度数.
21.用两种方法证明“三角形的一个外角等于其不相邻的两个内角之和”.如图,∠DAB是△ABC的一个外角.求证:∠DAB=∠B+∠C.
证法1:∵∠BAC+∠B+∠C=180°(??
)
∠BAC+∠DAB=180°(平角的定义)
∴∠BAC+∠B+∠C=∠BAC+∠DAB(??
)
∴∠DAB=∠B+∠C(??
)
请把证法1依据填充完整,并用不同的方法完成证法2.
22.??????????????????????????
(1)已知直线AB∥CD,点P为平行线AB,CD之间的一点.如图1,若∠ABP=50°,∠CDP=60°,BE平分∠ABP,DE平分∠CDP,求∠BED的度数.
(2)(探究)如图2,当点P在直线AB的上方时,若∠ABP=α,∠CDP=β,∠ABP和∠CDP的平分线交于点E1
,
∠ABE1与∠CDE1的角平分线交于点E2
,
∠ABE2与∠CDE2的角平分线交于点E3
,
…以此类推,求∠En的度数.
(3)(变式)如图3,∠ABP的角平分线的反向延长线和∠CDP的补角的角平分线交于点E,试猜想∠P与∠E的数量关系,并说明理由.
参考答案
1.
C
2.
B
3.
A
4.
A
5.
B
6.
C
7.
B
8.
D
9.
C
10.
A
11.
C
12.
C
13.
15°
14.
165°
15.
24
16.
260°
17.
4:3:2:1
18.
108
19.
证明:连接
∵
,
∴
?,
∵
,
,
,
,
∴
.
20.
解:因为AB∥CD,
所以∠CFE=∠ABE=60°.
因为∠D=50°,
所以∠E=∠CFE-∠D=60°-50°=10°.
21.
解:证法1:∵∠BAC+∠B+∠C=180°(三角形内角和定理),
∠BAC+∠DAB=180°(平角的定义),
∴∠BAC+∠B+∠C=∠BAC+∠DAB(等量代换),
∴∠DAB=∠B+∠C(等式性质);
证法2:过A点作AE∥BC,
∵AE∥BC,
∴∠DAE=∠C,
∠EAB=∠B,
又∵∠DAB=∠DAE+∠EAB,
∴∠DAB=∠B+∠C.
22.
(1)解:如图1,过E作EF∥AB,而AB∥CD,
∴AB∥CD∥EF,
∴∠ABE=∠FEB,∠CDE=∠FED,
∴∠BED=∠BEF+∠DEF=∠ABE+∠CDE,
又∵∠ABP=50°,∠CDP=60°,BE平分∠ABP,DE平分∠CDP,
∴∠ABE=
∠ABP=25°,∠CDE=
∠CDP=30°,
∴∠BED=25°+30°=55°,
故答案为55°;
(2)如图2,∵∠ABP和∠CDP的平分线交于点E1
,
∴∠ABE1=
∠ABP=
α,∠CDE1=
∠CDP=
,
∵AB∥CD,
∴∠CDF=∠AFE1=
,
∴∠E1=∠AFE1﹣∠ABE1=
﹣
α=
(β﹣α),
∵∠ABE1与∠CDE1的角平分线交于点E2
,
∴∠ABE2=
∠ABE1=
α,∠CDE2=
∠CDE1=
,
∵AB∥CD,
∴∠CDG=∠AGE2=
,
∴∠E2=∠AGE2﹣∠ABE2=
(β﹣α),
同理可得,∠E3=
(β﹣α),
以此类推,∠En的度数为
(β﹣α).
(3)∠DEB=90°﹣
∠P.理由如下:
如图3,过E作EG∥AB,而AB∥CD,
∴AB∥CD∥EG,
∴∠MBE=∠BEG,∠FDE=∠GED,
∴∠DEB=∠BEG+∠DEG=∠MBE+∠FDE=∠ABQ+∠FDE,
又∵∠ABP的角平分线的反向延长线和∠CDP的补角的角平分线交于点E,
∴∠FDE=
∠PDF=
(180°﹣∠CDP),∠ABQ=
∠ABP,
∴∠DEB=
∠ABP+
(180°﹣∠CDP)=90°﹣
(∠CDP﹣∠ABP),
∵AB∥CD,
∴∠CDP=∠AHP,
∴∠DEB=90°﹣
(∠CDP﹣∠ABP)=90°﹣
(∠AHP﹣∠ABP)=90°﹣
∠P.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
