数学人教A版选修2-3 1.1分类加法计数原理与分步乘法计数原理 (2课时)(27张PPT)
文档属性
| 名称 | 数学人教A版选修2-3 1.1分类加法计数原理与分步乘法计数原理 (2课时)(27张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 948.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-27 11:51:32 | ||
图片预览








文档简介
1.1 分类加法计数原理 与分步乘法计数原理
(第一课时)
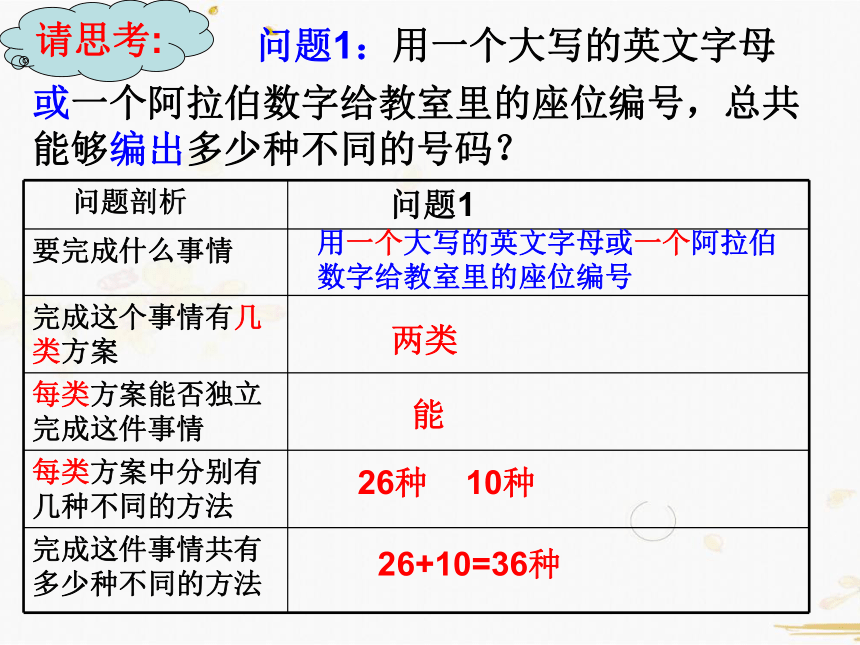
问题剖析
问题1
要完成什么事情
完成这个事情有几类方案
每类方案能否独立完成这件事情
每类方案中分别有几种不同的方法
完成这件事情共有多少种不同的方法
两类
能
26种 10种
26+10=36种
或一个阿拉伯数字给教室里的座位编号,总共能够编出多少种不同的号码?
请思考:
问题1:用一个大写的英文字母
用一个大写的英文字母或一个阿拉伯数字给教室里的座位编号
你能总结出这类问题的一般解决规律吗?
完成一件事有两类不同的方案,
在第1类方案中有m种不同的方法,
在第2类方案中有n种不同的方法,
那么完成这件事共有
N = m + n
种不同的方法。
例1.在填写高考志愿表时,一名高中毕业生了解到A,B两所大学各有一些自己感兴趣的强项专业,具体情况如下:
A大学
B大学
生物学
化学
医学
物理学
工程学
数学
会计学
信息技术学
法学
如果这名同学只能选一个专业,那么他共有多少种选择呢?
5+4=9
变式:在填写高考志愿表时,一名高中毕业生了解到,A,B,C三所大学各有一些自己感兴趣的强项专业,具体情况如下:
A大学
B大学
生物学
化学
医学
物理学
工程学
数学
会计学
信息技术学
法学
如果这名同学只能选一个专业,那么他共有多少种选择呢?
C大学
机械制造
建筑学
广告学
汉语言文学
韩语
N=5+4+5=14(种)
如果完成一件事情有n类不同方案,在每一类中都有若干种不同方法,那么应当如何计数呢?
完成一件事有 n 类不同的方案,
在第1类方案中有 m1 种不同的方法,
在第2类方案中有 m2 种不同的方法,
那么完成这件事共有
种不同的方法。
… …
在第n类方案中有mn种不同的方法,
思考:用前6个大写英文字母和1~9九个阿拉伯数字,以A1,A2,···,B1,B2,···的方式给教室里的座位编号,总共能编出多少种不同的号码?
分析:完成给教室里的座位编号编号这件事 分两
步完成:
第1步:先确定一个英文字母
第2步:再确定一个阿拉伯数字
字母 数字 得到的号码
1
2
3
4
5
6
7
8
9
A1
A2
A3
A4
A5
A6
A7
A8
A9
树形图
A
B
B1
B2
B3
B4
B5
B6
B7
B8
B9
C
C1
C2
C3
C4
C5
C6
C7
C8
C9
D
D1
D2
D3
D4
D5
D6
D7
D8
D9
E
E1
E2
E3
E4
E5
E6
E7
E8
E9
F
F1
F2
F3
F4
F5
F6
F7
F8
F9
分析:完成给教室里的座位编号这件事需要
两个步骤,
第1步,确定一个英文字母,有6种不同方法;
第2步,确定一个阿拉伯数字,有9种不同方法;
所以,编号共有6×9=54种方法.
那么完成这件事共有
种不同的方法。
完成一件事需要两个步骤,
做第1步有m种不同的方法,
做第2步有n种不同的方法,
那么完成这件事共有
种不同的方法。
完成一件事需要n个步骤,
做第1步有m1 种不同的方法,
做第2步有m2种不同的方法,
… …
做第n步有mn种不同的方法,
两个计数原理
分类加法计数原理
分步乘法计数原理
相同点
不同点
注意点
用来计算“完成一件事”的方法种数
每类方案中的每一种方法都能______ 完成这件事
每步_________才算完成这件事情
(每步中的每一种方法不能独立完成这件事)
类类相加
步步相乘
类类独立
步步相依
独立
依次完成
不重不漏
步骤完整
分类完成
分步完成
例2、设某班有男生30名,女生24名。现要从中选出男、女生各一名代表班级参加比赛,共有多少种不同的选法?
解:30×24=720
解:从书架上任取1本书,
例3 书架上的第1层放着4本不同的计算机书,第2层放着3本不同的文艺书,第3层放着2本不同的体育书。
第1类方法是从第1层取1本计算机书,有4种方法;
第2类方法是从第2层取1本文艺书,有3种方法;
第3类方法是从第3层取1本体育书,有2种方法。
根据分类加法计数原理,不同取法的种数是:N=4+3+2=9.
(1)从书架上任取1本书,有几种不同的取法?
有三类方法:
(2)从书架上的第1、2、3层各取1本书,有几种不同的取法?
例3 书架上的第1层放着4本不同的计算机书,第2层放着3本不同的文艺书,第3层放着2本不同的体育书。
(1)从书架上任取1本书,有几种不同的取法?
解:从书架的第1,2,3层各取1本书,
第1步:从第1层取1本计算机书,有4种方法;
第2步:从第2层取1本文艺书,有3种方法;
第3步:从第3层取1本体育书,有2种方法。
根据分步计数原理,不同取法的种数是:N=4×3×2=24.
可以分成三个步骤完成:
解答计数问题的一般思维过程:
完成一件什么事
如何完成这件事
利用加法原理进行计数
方法的分类
过程的分步
利用乘法原理进行计数
做练习
P6:第1、2、3题
作业布置
P12:A组 第1—5题
1.1 分类加法计数原理 与分步乘法技术原理
(第二课时)
共同点:
分类加法计数原理
分步乘法计数原理
①完成一件事有n类不同的方案;
②各类方案相互独立;
③每一类方案都能直接完成该事件。
完成一件事要n个不同的步骤;
每一个步骤都不能直接完成该事件,只有完成每个步骤,才能完成这件事。
各个步骤相互联系 ;
相互联系分步到达
相互独立
直达目的
都是有关“完成一件事情”的所有不同方法的种数问题。
主要不同点:
例6.给程序模块命名,需要用3个字符,其中首个字符要求用字母A~G或U~Z,后两个要求用数字1~9,问最多可以给多少个程序命名?
分析:要给一个程序模块命名,可以分三个步骤:第一步,选首字符;第二步,先中间字符;第三步,选末位字符。
解:首字符共有7+6=13种不同的选法,
答:最多可以给1053个程序命名。
中间字符和末位字符各有9种不同的选法
根据分步计数原理,最多可以有13×9×9=1053种不同的选法
例7.核糖核酸(RNA)分子是在生物细胞中发现的化学成分,一个RNA分子
是一个有着数百个甚至数千个位置的长链,长链中每一个位置上都由一种称
为碱基的化学成分所占据,总共有4个不同的碱基,分别用A,C,G,U表
示,在一个RNA分子中,各种碱基能够以任意次序出现,所以在任意一个位
置上的碱基与其他位置上的碱基无关。假设有一类RNA分子由100个碱基组
成,那么能有多少种不同的RNA分子?
U
U
U
A
A
A
C
C
C
G
G
G
分析:用100个位置表示由100个碱基组成的长链,每个位置都可以从A、C、G、U中任选一个来占据。
第1位
第2位
第3位
第100位
4种
4种
4种
4种
……
解:100个碱基组成的长链共有100个位置,在每个位置中,从A、C、G、U中任选一个来填入,每个位置有4种填充方法。根据分步计数原理,共有
种不同的RNA分子.
例8.电子元件很容易实现电路的通与断、电位的高与底等两种状态,而这也是最容易控制的两种状态。因此计算机内部就采用了每一位只有0或1两种数字的计数法,即二进制,为了使计算机能够识别字符,需要对字符进行编码,每个字符可以用一个或多个字节来表示,其中字节是计算机中数据存储的最小计量单位,每个字节由8个二进制位构成,问
(1)一个字节(8位)最多可以表示多少个不同的字符?
(2)计算机汉字国标码(GB码)包含了6763个汉字,一个汉字为一个字符,要对这些汉字进行编码,每个汉字至少要用多少个字节表示?
第1位
第2位
第3位
第8位
2种
2种
2种
2种
……
如00000000,10000000,
11111111.
开始
子模块1
18条执行路径
子模块3
28条执行路径
子模块2
45条执行路径
子模块5
43条执行路径
子模块4
38条执行路径
结束
A
例9.计算机编程人员在编写好程序以后要对程序进行测试。程序员需要知道到底有多少条执行路(即程序从开始到结束的线),以便知道需要提供多少个测试数据。一般的,一个程序模块又许多子模块组
成,它的一个具有许多执行路径的程序模块。问:这个程序模块有多少条执行路径?另外为了减少测试时间,程序员需要设法减少测试次数,你能帮助程序员设计一个测试方式,
以减少测试次数吗?
开始
子模块1
18条执行路径
子模块3
28条执行路径
子模块2
45条执行路径
子模块5
43条执行路径
子模块4
38条执行路径
结束
A
分析:整个模块的任意一条路径都分两步完成:第1步是从开始执行到A点;第2步是从A点执行到结束。而第步可由子模块1或子模块2或子模块3来完成;第二步可由子模块4或子模块5来完成。因此,分析一条指令在整个模块的执行路径需要用到两个计数原理。
开始
子模块1
18条执行路径
子模块3
28条执行路径
子模块2
45条执行路径
子模块5
43条执行路径
子模块4
38条执行路径
结束
A
再测试各个模块之间的信息交流是否正常,需要测试的次数为:3*2=6。
如果每个子模块都正常工作,并且各个子模块之间的信息交流也正常,那么整个程序模块就正常。
这样,测试整个模块的次数就变为
172+6=178(次)
2)在实际测试中,程序员总是把每一个子模块看成一个黑箱,即通过只考察是否执行了正确的子模块的方式来测试整个模块。这样,他可以先分别单独测试5个模块,以考察每个子模块的工作是否正常。总共需要的测试次数为:
18+45+28+38+43=172。
例10.随着人们生活水平的提高,某城市家庭汽车拥有量迅速增长,汽车牌照号码需要扩容。交通管理部门出台了一种汽车牌照组成办法,每一个汽车牌照都必须有3个不重复的英文字母和3个不重复的阿拉伯数字,并且3个字母必须合成一组出现,3个数字也必须合成一组出现,那么这种办法共能给多少辆汽车上牌照?
做P10练习
(第一课时)
问题剖析
问题1
要完成什么事情
完成这个事情有几类方案
每类方案能否独立完成这件事情
每类方案中分别有几种不同的方法
完成这件事情共有多少种不同的方法
两类
能
26种 10种
26+10=36种
或一个阿拉伯数字给教室里的座位编号,总共能够编出多少种不同的号码?
请思考:
问题1:用一个大写的英文字母
用一个大写的英文字母或一个阿拉伯数字给教室里的座位编号
你能总结出这类问题的一般解决规律吗?
完成一件事有两类不同的方案,
在第1类方案中有m种不同的方法,
在第2类方案中有n种不同的方法,
那么完成这件事共有
N = m + n
种不同的方法。
例1.在填写高考志愿表时,一名高中毕业生了解到A,B两所大学各有一些自己感兴趣的强项专业,具体情况如下:
A大学
B大学
生物学
化学
医学
物理学
工程学
数学
会计学
信息技术学
法学
如果这名同学只能选一个专业,那么他共有多少种选择呢?
5+4=9
变式:在填写高考志愿表时,一名高中毕业生了解到,A,B,C三所大学各有一些自己感兴趣的强项专业,具体情况如下:
A大学
B大学
生物学
化学
医学
物理学
工程学
数学
会计学
信息技术学
法学
如果这名同学只能选一个专业,那么他共有多少种选择呢?
C大学
机械制造
建筑学
广告学
汉语言文学
韩语
N=5+4+5=14(种)
如果完成一件事情有n类不同方案,在每一类中都有若干种不同方法,那么应当如何计数呢?
完成一件事有 n 类不同的方案,
在第1类方案中有 m1 种不同的方法,
在第2类方案中有 m2 种不同的方法,
那么完成这件事共有
种不同的方法。
… …
在第n类方案中有mn种不同的方法,
思考:用前6个大写英文字母和1~9九个阿拉伯数字,以A1,A2,···,B1,B2,···的方式给教室里的座位编号,总共能编出多少种不同的号码?
分析:完成给教室里的座位编号编号这件事 分两
步完成:
第1步:先确定一个英文字母
第2步:再确定一个阿拉伯数字
字母 数字 得到的号码
1
2
3
4
5
6
7
8
9
A1
A2
A3
A4
A5
A6
A7
A8
A9
树形图
A
B
B1
B2
B3
B4
B5
B6
B7
B8
B9
C
C1
C2
C3
C4
C5
C6
C7
C8
C9
D
D1
D2
D3
D4
D5
D6
D7
D8
D9
E
E1
E2
E3
E4
E5
E6
E7
E8
E9
F
F1
F2
F3
F4
F5
F6
F7
F8
F9
分析:完成给教室里的座位编号这件事需要
两个步骤,
第1步,确定一个英文字母,有6种不同方法;
第2步,确定一个阿拉伯数字,有9种不同方法;
所以,编号共有6×9=54种方法.
那么完成这件事共有
种不同的方法。
完成一件事需要两个步骤,
做第1步有m种不同的方法,
做第2步有n种不同的方法,
那么完成这件事共有
种不同的方法。
完成一件事需要n个步骤,
做第1步有m1 种不同的方法,
做第2步有m2种不同的方法,
… …
做第n步有mn种不同的方法,
两个计数原理
分类加法计数原理
分步乘法计数原理
相同点
不同点
注意点
用来计算“完成一件事”的方法种数
每类方案中的每一种方法都能______ 完成这件事
每步_________才算完成这件事情
(每步中的每一种方法不能独立完成这件事)
类类相加
步步相乘
类类独立
步步相依
独立
依次完成
不重不漏
步骤完整
分类完成
分步完成
例2、设某班有男生30名,女生24名。现要从中选出男、女生各一名代表班级参加比赛,共有多少种不同的选法?
解:30×24=720
解:从书架上任取1本书,
例3 书架上的第1层放着4本不同的计算机书,第2层放着3本不同的文艺书,第3层放着2本不同的体育书。
第1类方法是从第1层取1本计算机书,有4种方法;
第2类方法是从第2层取1本文艺书,有3种方法;
第3类方法是从第3层取1本体育书,有2种方法。
根据分类加法计数原理,不同取法的种数是:N=4+3+2=9.
(1)从书架上任取1本书,有几种不同的取法?
有三类方法:
(2)从书架上的第1、2、3层各取1本书,有几种不同的取法?
例3 书架上的第1层放着4本不同的计算机书,第2层放着3本不同的文艺书,第3层放着2本不同的体育书。
(1)从书架上任取1本书,有几种不同的取法?
解:从书架的第1,2,3层各取1本书,
第1步:从第1层取1本计算机书,有4种方法;
第2步:从第2层取1本文艺书,有3种方法;
第3步:从第3层取1本体育书,有2种方法。
根据分步计数原理,不同取法的种数是:N=4×3×2=24.
可以分成三个步骤完成:
解答计数问题的一般思维过程:
完成一件什么事
如何完成这件事
利用加法原理进行计数
方法的分类
过程的分步
利用乘法原理进行计数
做练习
P6:第1、2、3题
作业布置
P12:A组 第1—5题
1.1 分类加法计数原理 与分步乘法技术原理
(第二课时)
共同点:
分类加法计数原理
分步乘法计数原理
①完成一件事有n类不同的方案;
②各类方案相互独立;
③每一类方案都能直接完成该事件。
完成一件事要n个不同的步骤;
每一个步骤都不能直接完成该事件,只有完成每个步骤,才能完成这件事。
各个步骤相互联系 ;
相互联系分步到达
相互独立
直达目的
都是有关“完成一件事情”的所有不同方法的种数问题。
主要不同点:
例6.给程序模块命名,需要用3个字符,其中首个字符要求用字母A~G或U~Z,后两个要求用数字1~9,问最多可以给多少个程序命名?
分析:要给一个程序模块命名,可以分三个步骤:第一步,选首字符;第二步,先中间字符;第三步,选末位字符。
解:首字符共有7+6=13种不同的选法,
答:最多可以给1053个程序命名。
中间字符和末位字符各有9种不同的选法
根据分步计数原理,最多可以有13×9×9=1053种不同的选法
例7.核糖核酸(RNA)分子是在生物细胞中发现的化学成分,一个RNA分子
是一个有着数百个甚至数千个位置的长链,长链中每一个位置上都由一种称
为碱基的化学成分所占据,总共有4个不同的碱基,分别用A,C,G,U表
示,在一个RNA分子中,各种碱基能够以任意次序出现,所以在任意一个位
置上的碱基与其他位置上的碱基无关。假设有一类RNA分子由100个碱基组
成,那么能有多少种不同的RNA分子?
U
U
U
A
A
A
C
C
C
G
G
G
分析:用100个位置表示由100个碱基组成的长链,每个位置都可以从A、C、G、U中任选一个来占据。
第1位
第2位
第3位
第100位
4种
4种
4种
4种
……
解:100个碱基组成的长链共有100个位置,在每个位置中,从A、C、G、U中任选一个来填入,每个位置有4种填充方法。根据分步计数原理,共有
种不同的RNA分子.
例8.电子元件很容易实现电路的通与断、电位的高与底等两种状态,而这也是最容易控制的两种状态。因此计算机内部就采用了每一位只有0或1两种数字的计数法,即二进制,为了使计算机能够识别字符,需要对字符进行编码,每个字符可以用一个或多个字节来表示,其中字节是计算机中数据存储的最小计量单位,每个字节由8个二进制位构成,问
(1)一个字节(8位)最多可以表示多少个不同的字符?
(2)计算机汉字国标码(GB码)包含了6763个汉字,一个汉字为一个字符,要对这些汉字进行编码,每个汉字至少要用多少个字节表示?
第1位
第2位
第3位
第8位
2种
2种
2种
2种
……
如00000000,10000000,
11111111.
开始
子模块1
18条执行路径
子模块3
28条执行路径
子模块2
45条执行路径
子模块5
43条执行路径
子模块4
38条执行路径
结束
A
例9.计算机编程人员在编写好程序以后要对程序进行测试。程序员需要知道到底有多少条执行路(即程序从开始到结束的线),以便知道需要提供多少个测试数据。一般的,一个程序模块又许多子模块组
成,它的一个具有许多执行路径的程序模块。问:这个程序模块有多少条执行路径?另外为了减少测试时间,程序员需要设法减少测试次数,你能帮助程序员设计一个测试方式,
以减少测试次数吗?
开始
子模块1
18条执行路径
子模块3
28条执行路径
子模块2
45条执行路径
子模块5
43条执行路径
子模块4
38条执行路径
结束
A
分析:整个模块的任意一条路径都分两步完成:第1步是从开始执行到A点;第2步是从A点执行到结束。而第步可由子模块1或子模块2或子模块3来完成;第二步可由子模块4或子模块5来完成。因此,分析一条指令在整个模块的执行路径需要用到两个计数原理。
开始
子模块1
18条执行路径
子模块3
28条执行路径
子模块2
45条执行路径
子模块5
43条执行路径
子模块4
38条执行路径
结束
A
再测试各个模块之间的信息交流是否正常,需要测试的次数为:3*2=6。
如果每个子模块都正常工作,并且各个子模块之间的信息交流也正常,那么整个程序模块就正常。
这样,测试整个模块的次数就变为
172+6=178(次)
2)在实际测试中,程序员总是把每一个子模块看成一个黑箱,即通过只考察是否执行了正确的子模块的方式来测试整个模块。这样,他可以先分别单独测试5个模块,以考察每个子模块的工作是否正常。总共需要的测试次数为:
18+45+28+38+43=172。
例10.随着人们生活水平的提高,某城市家庭汽车拥有量迅速增长,汽车牌照号码需要扩容。交通管理部门出台了一种汽车牌照组成办法,每一个汽车牌照都必须有3个不重复的英文字母和3个不重复的阿拉伯数字,并且3个字母必须合成一组出现,3个数字也必须合成一组出现,那么这种办法共能给多少辆汽车上牌照?
做P10练习
