数学人教A版选修2-3 2.2.1条件概率(16张PPT)
文档属性
| 名称 | 数学人教A版选修2-3 2.2.1条件概率(16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-27 00:00:00 | ||
图片预览





文档简介
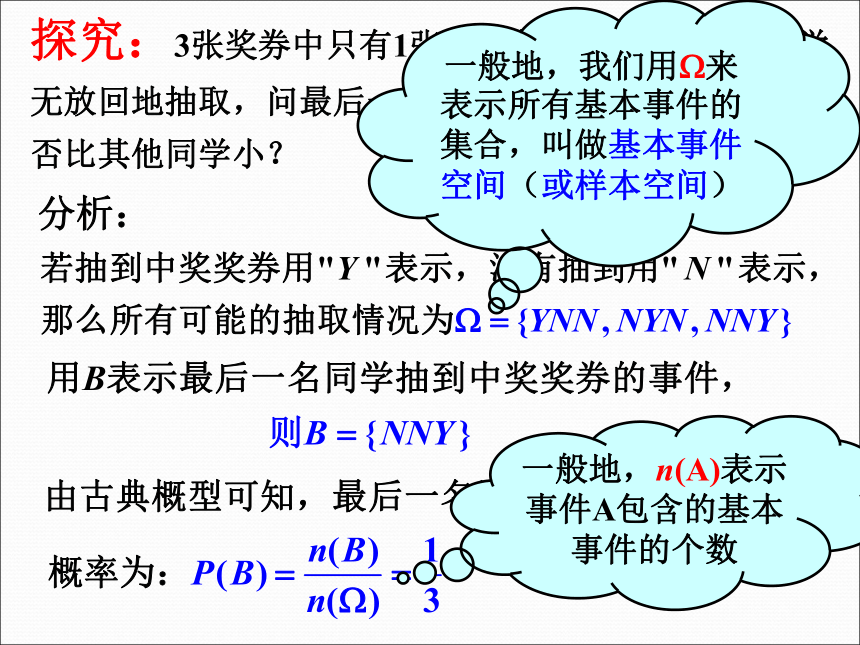
探究:3张奖券中只有1张能中奖,现分别由3名同学
无放回地抽取,问最后一名同学抽到中奖奖券的概率是
否比其他同学小?
分析:
一般地,我们用W来表示所有基本事件的集合,叫做基本事件空间(或样本空间)
一般地,n(A)表示
事件A包含的基本
事件的个数
思考:如果已经知道第一名同学没有抽到中奖奖券,
那么最后一名抽到中奖奖券的概率又是多少?
分析:
不妨设“第一名同学没有抽到中奖奖券”为事件A,
注:P(B|A)表示在事件A发生的条件下B发生的概率
你知道第一名同学的抽奖结果为什么会影响最后一名同学的抽奖结果吗?
分析:
若不知道第一名同学的抽奖结果,则样本空间为、
若知道了第一名同学的抽奖结果,则样本空间变成
但因为最后一名中奖的情况只有一种{NNY}
故概率会发生变化
思考:你知道第一名同学的抽奖结果为什么会影响最后一名同学的抽奖结果吗?
分析:求P(B|A)的一般思想
因为已经知道事件A必然发生,所以只需在A发生
的范围内考虑问题,即现在的样本空间为A。
因为在事件A发生的情况下事件B发生,等价于事
件A和事件B同时发生,即AB发生。
故其条件概率为
为了把条件概率推广到一般情形,不妨记原来的
样本空间为W,则有
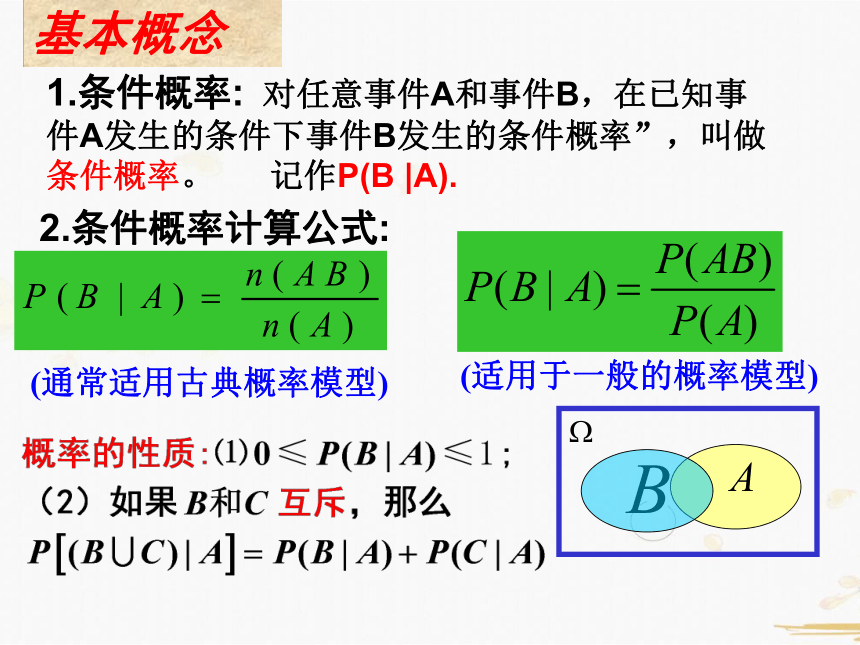
1.条件概率: 对任意事件A和事件B,在已知事件A发生的条件下事件B发生的条件概率”,叫做条件概率。 记作P(B |A).
2.条件概率计算公式:
(通常适用古典概率模型)
(适用于一般的概率模型)
基本概念
3.概率 P(B|A)与P(AB)的区别与联系
例1、在5道题中有3道理科题和2道文科题,如果不放回
地依次抽取2道题,求:
(1)第一次抽取到理科题的概率;
(2)第一次和第二次都抽取到理科题的概率;
解:设第1次抽到理科题为事件A,第2次抽到理科题为事件B,则第1次和第2次都抽到理科题为事件AB.
(1)从5道题中不放回地依次抽取2道的事件数为
例1、在5道题中有3道理科题和2道文科题,如果不放回
地依次抽取2道题,求:
(1)第一次抽取到理科题的概率;
(2)第一次和第二次都抽取到理科题的概率;
解:设第1次抽到理科题为事件A,第2次抽到理科题为事件B,则第1次和第2次都抽到理科题为事件AB.
例1、在5道题中有3道理科题和2道文科题,如果不放回
地依次抽取2道题,求:
(1)第一次抽取到理科题的概率;
(2)第一次和第二次都抽取到理科题的概率;
(3)在第一次抽到理科题的条件下,第二次抽到理科题
的概率。
(3)解法一:由(1)(2)可得,在第一次抽到理科题的条件下,第二次抽到理科题的概率为
例1、在5道题中有3道理科题和2道文科题,如果不放回
地依次抽取2道题,求:
(1)第一次抽取到理科题的概率;
(2)第一次和第二次都抽取到理科题的概率;
(3)在第一次抽到理科题的条件下,第二次抽到理科题
的概率。
(3)解法二:因为n(AB)=6,n(A)=12,所以
解法三:
第一次抽到理科题,则还剩下两道理科、两道文科题,故第二次抽到理科题的概率为1/2
一批同型号产品由甲、乙两厂生产,产品
结构如下表:
练习:
厂别
甲厂
乙厂
合计
数量
等级
合格品
次 品
合 计
(1)从这批产品中随意地取一件,则这件产品恰好是
次品的概率是_________;
(2)在已知取出的产品是甲厂生产的,则这件产品恰好
是次品的概率是_________;
例2、一张储蓄卡的密码共有6位数字,每位数字都可
从0~9中任选一个,某人在银行自动提款机上取钱时,
忘记了密码的最后一位数字,求
(1)任意按最后一位数字,不超过2次就按对的概率;
(2)如果他记得密码的最后一位是偶数,不超过2次
就按对的概率。
例2、一张储蓄卡的密码共有6位数字,每位数字都可
从0~9中任选一个,某人在银行自动提款机上取钱时,
忘记了密码的最后一位数字,求
(1)任意按最后一位数字,不超过2次就按对的概率;
(2)如果他记得密码的最后一位是偶数,不超过2次
就按对的概率。
做P54练习第1、2题
作业布置:
1、完成好《全优课堂》
2、预习下一节新课内容
小结:
1、条件概率的定义:
2、条件概率的计算公式
设A,B为两个事件,则在事件A发生的条件下,
事件B发生的概率就叫做的条件概率
无放回地抽取,问最后一名同学抽到中奖奖券的概率是
否比其他同学小?
分析:
一般地,我们用W来表示所有基本事件的集合,叫做基本事件空间(或样本空间)
一般地,n(A)表示
事件A包含的基本
事件的个数
思考:如果已经知道第一名同学没有抽到中奖奖券,
那么最后一名抽到中奖奖券的概率又是多少?
分析:
不妨设“第一名同学没有抽到中奖奖券”为事件A,
注:P(B|A)表示在事件A发生的条件下B发生的概率
你知道第一名同学的抽奖结果为什么会影响最后一名同学的抽奖结果吗?
分析:
若不知道第一名同学的抽奖结果,则样本空间为、
若知道了第一名同学的抽奖结果,则样本空间变成
但因为最后一名中奖的情况只有一种{NNY}
故概率会发生变化
思考:你知道第一名同学的抽奖结果为什么会影响最后一名同学的抽奖结果吗?
分析:求P(B|A)的一般思想
因为已经知道事件A必然发生,所以只需在A发生
的范围内考虑问题,即现在的样本空间为A。
因为在事件A发生的情况下事件B发生,等价于事
件A和事件B同时发生,即AB发生。
故其条件概率为
为了把条件概率推广到一般情形,不妨记原来的
样本空间为W,则有
1.条件概率: 对任意事件A和事件B,在已知事件A发生的条件下事件B发生的条件概率”,叫做条件概率。 记作P(B |A).
2.条件概率计算公式:
(通常适用古典概率模型)
(适用于一般的概率模型)
基本概念
3.概率 P(B|A)与P(AB)的区别与联系
例1、在5道题中有3道理科题和2道文科题,如果不放回
地依次抽取2道题,求:
(1)第一次抽取到理科题的概率;
(2)第一次和第二次都抽取到理科题的概率;
解:设第1次抽到理科题为事件A,第2次抽到理科题为事件B,则第1次和第2次都抽到理科题为事件AB.
(1)从5道题中不放回地依次抽取2道的事件数为
例1、在5道题中有3道理科题和2道文科题,如果不放回
地依次抽取2道题,求:
(1)第一次抽取到理科题的概率;
(2)第一次和第二次都抽取到理科题的概率;
解:设第1次抽到理科题为事件A,第2次抽到理科题为事件B,则第1次和第2次都抽到理科题为事件AB.
例1、在5道题中有3道理科题和2道文科题,如果不放回
地依次抽取2道题,求:
(1)第一次抽取到理科题的概率;
(2)第一次和第二次都抽取到理科题的概率;
(3)在第一次抽到理科题的条件下,第二次抽到理科题
的概率。
(3)解法一:由(1)(2)可得,在第一次抽到理科题的条件下,第二次抽到理科题的概率为
例1、在5道题中有3道理科题和2道文科题,如果不放回
地依次抽取2道题,求:
(1)第一次抽取到理科题的概率;
(2)第一次和第二次都抽取到理科题的概率;
(3)在第一次抽到理科题的条件下,第二次抽到理科题
的概率。
(3)解法二:因为n(AB)=6,n(A)=12,所以
解法三:
第一次抽到理科题,则还剩下两道理科、两道文科题,故第二次抽到理科题的概率为1/2
一批同型号产品由甲、乙两厂生产,产品
结构如下表:
练习:
厂别
甲厂
乙厂
合计
数量
等级
合格品
次 品
合 计
(1)从这批产品中随意地取一件,则这件产品恰好是
次品的概率是_________;
(2)在已知取出的产品是甲厂生产的,则这件产品恰好
是次品的概率是_________;
例2、一张储蓄卡的密码共有6位数字,每位数字都可
从0~9中任选一个,某人在银行自动提款机上取钱时,
忘记了密码的最后一位数字,求
(1)任意按最后一位数字,不超过2次就按对的概率;
(2)如果他记得密码的最后一位是偶数,不超过2次
就按对的概率。
例2、一张储蓄卡的密码共有6位数字,每位数字都可
从0~9中任选一个,某人在银行自动提款机上取钱时,
忘记了密码的最后一位数字,求
(1)任意按最后一位数字,不超过2次就按对的概率;
(2)如果他记得密码的最后一位是偶数,不超过2次
就按对的概率。
做P54练习第1、2题
作业布置:
1、完成好《全优课堂》
2、预习下一节新课内容
小结:
1、条件概率的定义:
2、条件概率的计算公式
设A,B为两个事件,则在事件A发生的条件下,
事件B发生的概率就叫做的条件概率
