数学人教A版选修2-3 2.3.2离散型随机变量的方差(32张PPT)
文档属性
| 名称 | 数学人教A版选修2-3 2.3.2离散型随机变量的方差(32张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-27 12:15:37 | ||
图片预览









文档简介
一、离散型随机变量的均值
数学期望
···
···
···
···
二、离散型随机变量均值的线性性质
三、两点分布与二项分布的均值
X
X服从两点分布
X~B(n,p)
E(X)
探究思考
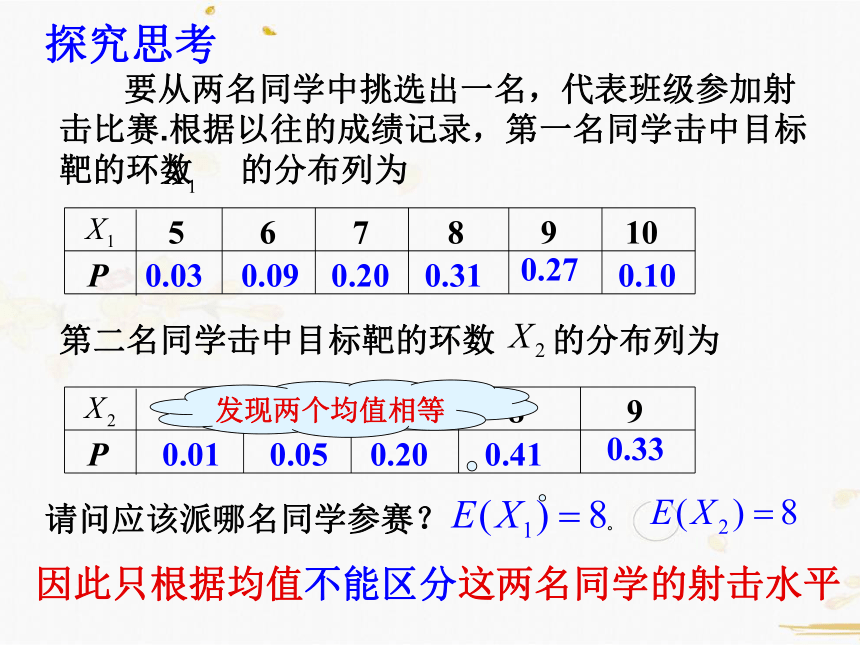
要从两名同学中挑选出一名,代表班级参加射击比赛.根据以往的成绩记录,第一名同学击中目标靶的环数 的分布列为
P
5
6
7
8
9
10
0.03
0.09
0.20
0.31
0.27
0.10
第二名同学击中目标靶的环数 的分布列为
P
5
6
7
8
9
0.01
0.05
0.20
0.41
0.33
请问应该派哪名同学参赛?
发现两个均值相等
因此只根据均值不能区分这两名同学的射击水平
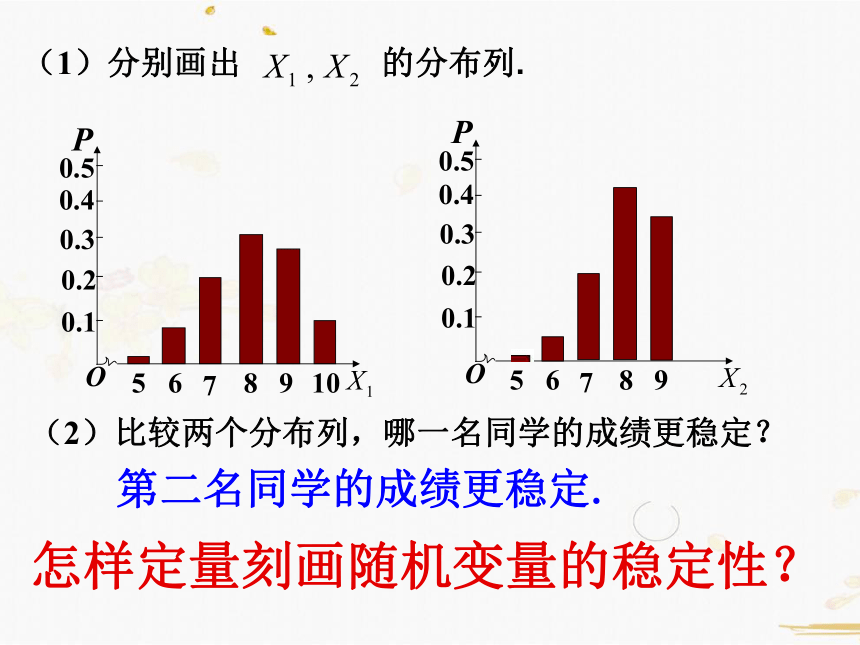
(1)分别画出 的分布列.
O
5
6
7
10
9
8
P
0.1
0.2
0.3
0.4
0.5
O
5
6
7
9
8
P
0.1
0.2
0.3
0.4
0.5
(2)比较两个分布列,哪一名同学的成绩更稳定?
第二名同学的成绩更稳定.
怎样定量刻画随机变量的稳定性?
为这些偏离程度的加权平均,刻画了随机变量 X 与其均值 E(X) 的平均偏离程度. 称 D(X)为随机变量 X 的方差.
称 为随机变量X的标准差.
随机变量X 的方差
设离散型随机变量 X 的分布列为
X
P
…
…
…
…
则 描述了 相对于均值
的偏离程度.而
方差D(X)是一个用来体现随机变量X 取值分散程度的量.如果D(X)值大, 表示X 取值分散程度大, E(X)的代表性差;而如果D(X)值小,则表示X 的取值比较集中,以E(X)作为随机变量的代表性好.
方差的意义
请分别计算探究中两名同学各自的射击成绩的方差.
P
5
6
7
8
9
10
0.03
0.09
0.20
0.31
0.27
0.10
P
5
6
7
8
9
0.01
0.05
0.20
0.41
0.33
结论:第一名同学的射击成绩稳定性较差,第二名同学的射击成绩稳定性较好,稳定于8环左右.
例、随机抛掷一枚质地均匀的骰子,求向上一面的点数的均值、方差和标准差.
解:抛掷散子所得点数X 的分布列为
P
6
5
4
3
2
1
X
;
.
几个常用公式:
推论:常数的方差为_______.
0
练习:
117
10
0.8
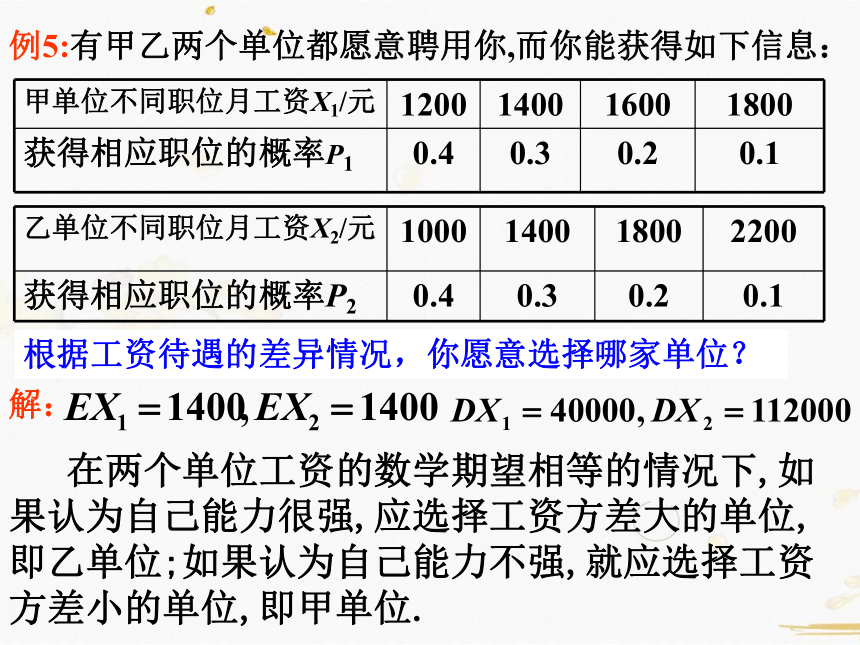
例5:有甲乙两个单位都愿意聘用你,而你能获得如下信息:
甲单位不同职位月工资X1/元
1200
1400
1600
1800
获得相应职位的概率P1
0.4
0.3
0.2
0.1
乙单位不同职位月工资X2/元
1000
1400
1800
2200
获得相应职位的概率P2
0.4
0.3
0.2
0.1
根据工资待遇的差异情况,你愿意选择哪家单位?
解:
在两个单位工资的数学期望相等的情况下,如果认为自己能力很强,应选择工资方差大的单位,即乙单位;如果认为自己能力不强,就应选择工资方差小的单位,即甲单位.
做练习:
P68 第1、2题
P68 A组:第1、5题
作业布置:
1、完成好《全优课堂》
2、预习新课2.4
*
对随机变量X的均值(期望)的理解:
(1)均值是算术平均值概念的推广,是概率意义上的平均;
(2)E(X)是一个实数,由X的分布列唯一确定,也就是说随
机变量X可以取不同的值,而E(X)是不变的,它描述的是
X取值的平均状态;
(3)E(X)的公式直接给出了E(X)的求法.
*
(2010·衡阳模拟)一厂家向用户提供的一箱产品共10件,其中有n件次品,用户先对产品进行抽检以决定是否接收.抽检规则是这样的:一次取一件产品检查(取出的产品不放回箱子),若前三次没有抽查到次品,则用户接收这箱产品;若前三次中一抽查到次品就立即停止抽检,并且用户拒绝接收这箱产品.
(1)若这箱产品被用户接收的概率是 ,求n的值;
(2)在(1)的条件下,记抽检的产品件数为X,求X的分布列和数学期望.
*
(1)利用古典概型易求.?
(2)X的取值为1、2、3,求出分布列代入期望
公式.
*
【解】 (1)设“这箱产品被用户接收”为事件A,
∴n=2.
(2)X的可能取值为1,2,3.
P(A)=
P(X=1)=
P(X=2)=
P(X=3)=
*
∴X的概率分布列为:
X
1
2
3
P
*
1.(2010·河南六市联考)甲、乙、丙、丁四人参加一家公司的招聘面试.公司规定面试合格者可签约.甲、乙面试合格 就签约;丙、丁面试都合格则一同签约,否则两人都不签
约.设每人面试合格的概率都是 ,且面试是否合格互不影响.求:
(1)至少有三人面试合格的概率;
(2)恰有两人签约的概率;
(3)签约人数的数学期望.
*
解:(1)设“至少有3人面试合格”为事件A,
则P(A)=
(2)设“恰有2人签约”为事件B,
“甲、乙两人签约,丙、丁两人都不签约”为事件B1;
“甲、乙两人都不签约,丙、丁两人签约”为事件B2;
则:B=B1+B2
P(B)=P(B1)+P(B2)
*
(3)设X为签约人数.
X的分布列如下:
P(X=0)=
P(X=1)=
P(X=2)=
P(X=3)=
P(X=4)=
*
X
0
1
2
3
4
P
*
(2010·贵阳模拟)有甲、乙两个建材厂,都想投标参加某重点建设,为了对重点建设负责,政府到两建材厂抽样检查,他们从中各抽取等量的样品检查它们的抗拉强度指标,其分布列如下:
*
举一反三
1. 某有奖竞猜活动设有A、B两组相互独立的问题,答对问题A可赢得奖金3万元,答对问题B可赢得奖金6万元.规定答题顺序可任选,但只有一个问题答对后才能解答下一个问题,否则中止答题.假设你答对问题A、B的概率依次为 、 .若你按先A后B的次序答题,写出你获得奖金的数额ξ的分布列及期望值Eξ.
ξ
0
3
9
p
解析: 若按先A后B的次序答题,获得奖金数额ξ的可取值为0,3(万元),9(万元).
∵P(ξ=0)= , P(ξ=3)= ,
P(ξ=9)= . ∴ξ的分布列为
*
题型二 求随机变量的方差
【例2】编号1,2,3的三位学生随意入座编号1,2,3的三个座位,每位学生坐一个座位,设与座位编号相同的学生人数是X.
(1)求随机变量X的概率分布列;
(2)求随机变量X的期望与方差.
ξ的数学期望为E(ξ)=
*
分析 (1)随机变量X的意义是对号入座的学生个数,所有取值为0,1,3.若有两人对号入座,则第三人必对号入座.由排列与等可能事件概率易求分布列;
(2)直接利用数学期望与方差公式求解.
X
0
1
3
P
解 (1)P(X=0)= ,P(X=1)= ,
P(X=3)= ,
故X的概率分布列为
(2)E(X)=
D(X)=
*
举一反三
2. 设在15个同类型的零件中有2个次品,每次任取1个,共取3次,并且每次取出后不再放回.若用X表示取出次品的个数.
(1)求X的分布列;
(2)求X的均值E(X)和方差D(X).
学后反思 求离散型随机变量X的方差的步骤:
(1)写出X的所有取值;
(2)计算P(X=xi);
(3)写出分布列,并求出期望E(X);
(4)由方差的定义求出D(X).
*
解析: (1)P(X=0)= , P(X=1)= ,
P(X=2)= .
故X的分布列为
(2)X的均值E(X)和方差D(X)分别为
E(X)= ;
D(X)=
X
0
1
2
P
*
题型四 期望与方差的综合应用
【例4】(14分)(2008·广东)随机抽取某厂的某种产品200件,经质检,其中有一等品126件,二等品50件,三等品20件,次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而生产1件次品亏损2万元,设1件产品的利润(单位:万元)为ξ.
(1)求ξ的分布列;
(2)求1件产品的平均利润(即ξ的数学期望);
(3)经技术革新后,仍有四个等级的产品,但次品率降为1%,一等品率提高为70%,如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
*
分析 求ξ的分布列时,要先求ξ取各值时的概率.
解 (1)ξ的所有可能取值有6,2,1,-2……………………1′
P(ξ=6)= =0.63,…………………………………..2′
P(ξ=2)= =0.25,…………………………………..3′
P(ξ=1)= =0.1,…………………………………4′
P(ξ=-2)= …………………………………..5′
故ξ的分布列为
……………………………………………………………………7′
ξ
6
2
1
-2
p
0.63
0.25
0.1
0.02
*
(2)E(ξ)=6×0.63+2×0.25+1×0.1+(-2)×0.02=4.34
………………………………………………………………..9′
(3)设技术革新后的三等品率为x,则此时1件产品的平均利润为
E(ξ)=6×0.7+2×(1-0.7-0.01-x)+1×x+(-2)×0.01
=4.76-x(0≤x≤0.29)……………………………………….12′
依题意,E(ξ)≥4.73,即4.76-x≥4.73,解得x≤0.03……13′
所以三等品率最多为3%..............................14′
学后反思 本题主要考查学生运用知识,迁移知识的能力.解决该类实际问题的关键是将实际问题化为数学问题,利用已学的知识进行处理,这也是今后高考的一大热点.
数学期望
···
···
···
···
二、离散型随机变量均值的线性性质
三、两点分布与二项分布的均值
X
X服从两点分布
X~B(n,p)
E(X)
探究思考
要从两名同学中挑选出一名,代表班级参加射击比赛.根据以往的成绩记录,第一名同学击中目标靶的环数 的分布列为
P
5
6
7
8
9
10
0.03
0.09
0.20
0.31
0.27
0.10
第二名同学击中目标靶的环数 的分布列为
P
5
6
7
8
9
0.01
0.05
0.20
0.41
0.33
请问应该派哪名同学参赛?
发现两个均值相等
因此只根据均值不能区分这两名同学的射击水平
(1)分别画出 的分布列.
O
5
6
7
10
9
8
P
0.1
0.2
0.3
0.4
0.5
O
5
6
7
9
8
P
0.1
0.2
0.3
0.4
0.5
(2)比较两个分布列,哪一名同学的成绩更稳定?
第二名同学的成绩更稳定.
怎样定量刻画随机变量的稳定性?
为这些偏离程度的加权平均,刻画了随机变量 X 与其均值 E(X) 的平均偏离程度. 称 D(X)为随机变量 X 的方差.
称 为随机变量X的标准差.
随机变量X 的方差
设离散型随机变量 X 的分布列为
X
P
…
…
…
…
则 描述了 相对于均值
的偏离程度.而
方差D(X)是一个用来体现随机变量X 取值分散程度的量.如果D(X)值大, 表示X 取值分散程度大, E(X)的代表性差;而如果D(X)值小,则表示X 的取值比较集中,以E(X)作为随机变量的代表性好.
方差的意义
请分别计算探究中两名同学各自的射击成绩的方差.
P
5
6
7
8
9
10
0.03
0.09
0.20
0.31
0.27
0.10
P
5
6
7
8
9
0.01
0.05
0.20
0.41
0.33
结论:第一名同学的射击成绩稳定性较差,第二名同学的射击成绩稳定性较好,稳定于8环左右.
例、随机抛掷一枚质地均匀的骰子,求向上一面的点数的均值、方差和标准差.
解:抛掷散子所得点数X 的分布列为
P
6
5
4
3
2
1
X
;
.
几个常用公式:
推论:常数的方差为_______.
0
练习:
117
10
0.8
例5:有甲乙两个单位都愿意聘用你,而你能获得如下信息:
甲单位不同职位月工资X1/元
1200
1400
1600
1800
获得相应职位的概率P1
0.4
0.3
0.2
0.1
乙单位不同职位月工资X2/元
1000
1400
1800
2200
获得相应职位的概率P2
0.4
0.3
0.2
0.1
根据工资待遇的差异情况,你愿意选择哪家单位?
解:
在两个单位工资的数学期望相等的情况下,如果认为自己能力很强,应选择工资方差大的单位,即乙单位;如果认为自己能力不强,就应选择工资方差小的单位,即甲单位.
做练习:
P68 第1、2题
P68 A组:第1、5题
作业布置:
1、完成好《全优课堂》
2、预习新课2.4
*
对随机变量X的均值(期望)的理解:
(1)均值是算术平均值概念的推广,是概率意义上的平均;
(2)E(X)是一个实数,由X的分布列唯一确定,也就是说随
机变量X可以取不同的值,而E(X)是不变的,它描述的是
X取值的平均状态;
(3)E(X)的公式直接给出了E(X)的求法.
*
(2010·衡阳模拟)一厂家向用户提供的一箱产品共10件,其中有n件次品,用户先对产品进行抽检以决定是否接收.抽检规则是这样的:一次取一件产品检查(取出的产品不放回箱子),若前三次没有抽查到次品,则用户接收这箱产品;若前三次中一抽查到次品就立即停止抽检,并且用户拒绝接收这箱产品.
(1)若这箱产品被用户接收的概率是 ,求n的值;
(2)在(1)的条件下,记抽检的产品件数为X,求X的分布列和数学期望.
*
(1)利用古典概型易求.?
(2)X的取值为1、2、3,求出分布列代入期望
公式.
*
【解】 (1)设“这箱产品被用户接收”为事件A,
∴n=2.
(2)X的可能取值为1,2,3.
P(A)=
P(X=1)=
P(X=2)=
P(X=3)=
*
∴X的概率分布列为:
X
1
2
3
P
*
1.(2010·河南六市联考)甲、乙、丙、丁四人参加一家公司的招聘面试.公司规定面试合格者可签约.甲、乙面试合格 就签约;丙、丁面试都合格则一同签约,否则两人都不签
约.设每人面试合格的概率都是 ,且面试是否合格互不影响.求:
(1)至少有三人面试合格的概率;
(2)恰有两人签约的概率;
(3)签约人数的数学期望.
*
解:(1)设“至少有3人面试合格”为事件A,
则P(A)=
(2)设“恰有2人签约”为事件B,
“甲、乙两人签约,丙、丁两人都不签约”为事件B1;
“甲、乙两人都不签约,丙、丁两人签约”为事件B2;
则:B=B1+B2
P(B)=P(B1)+P(B2)
*
(3)设X为签约人数.
X的分布列如下:
P(X=0)=
P(X=1)=
P(X=2)=
P(X=3)=
P(X=4)=
*
X
0
1
2
3
4
P
*
(2010·贵阳模拟)有甲、乙两个建材厂,都想投标参加某重点建设,为了对重点建设负责,政府到两建材厂抽样检查,他们从中各抽取等量的样品检查它们的抗拉强度指标,其分布列如下:
*
举一反三
1. 某有奖竞猜活动设有A、B两组相互独立的问题,答对问题A可赢得奖金3万元,答对问题B可赢得奖金6万元.规定答题顺序可任选,但只有一个问题答对后才能解答下一个问题,否则中止答题.假设你答对问题A、B的概率依次为 、 .若你按先A后B的次序答题,写出你获得奖金的数额ξ的分布列及期望值Eξ.
ξ
0
3
9
p
解析: 若按先A后B的次序答题,获得奖金数额ξ的可取值为0,3(万元),9(万元).
∵P(ξ=0)= , P(ξ=3)= ,
P(ξ=9)= . ∴ξ的分布列为
*
题型二 求随机变量的方差
【例2】编号1,2,3的三位学生随意入座编号1,2,3的三个座位,每位学生坐一个座位,设与座位编号相同的学生人数是X.
(1)求随机变量X的概率分布列;
(2)求随机变量X的期望与方差.
ξ的数学期望为E(ξ)=
*
分析 (1)随机变量X的意义是对号入座的学生个数,所有取值为0,1,3.若有两人对号入座,则第三人必对号入座.由排列与等可能事件概率易求分布列;
(2)直接利用数学期望与方差公式求解.
X
0
1
3
P
解 (1)P(X=0)= ,P(X=1)= ,
P(X=3)= ,
故X的概率分布列为
(2)E(X)=
D(X)=
*
举一反三
2. 设在15个同类型的零件中有2个次品,每次任取1个,共取3次,并且每次取出后不再放回.若用X表示取出次品的个数.
(1)求X的分布列;
(2)求X的均值E(X)和方差D(X).
学后反思 求离散型随机变量X的方差的步骤:
(1)写出X的所有取值;
(2)计算P(X=xi);
(3)写出分布列,并求出期望E(X);
(4)由方差的定义求出D(X).
*
解析: (1)P(X=0)= , P(X=1)= ,
P(X=2)= .
故X的分布列为
(2)X的均值E(X)和方差D(X)分别为
E(X)= ;
D(X)=
X
0
1
2
P
*
题型四 期望与方差的综合应用
【例4】(14分)(2008·广东)随机抽取某厂的某种产品200件,经质检,其中有一等品126件,二等品50件,三等品20件,次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而生产1件次品亏损2万元,设1件产品的利润(单位:万元)为ξ.
(1)求ξ的分布列;
(2)求1件产品的平均利润(即ξ的数学期望);
(3)经技术革新后,仍有四个等级的产品,但次品率降为1%,一等品率提高为70%,如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
*
分析 求ξ的分布列时,要先求ξ取各值时的概率.
解 (1)ξ的所有可能取值有6,2,1,-2……………………1′
P(ξ=6)= =0.63,…………………………………..2′
P(ξ=2)= =0.25,…………………………………..3′
P(ξ=1)= =0.1,…………………………………4′
P(ξ=-2)= …………………………………..5′
故ξ的分布列为
……………………………………………………………………7′
ξ
6
2
1
-2
p
0.63
0.25
0.1
0.02
*
(2)E(ξ)=6×0.63+2×0.25+1×0.1+(-2)×0.02=4.34
………………………………………………………………..9′
(3)设技术革新后的三等品率为x,则此时1件产品的平均利润为
E(ξ)=6×0.7+2×(1-0.7-0.01-x)+1×x+(-2)×0.01
=4.76-x(0≤x≤0.29)……………………………………….12′
依题意,E(ξ)≥4.73,即4.76-x≥4.73,解得x≤0.03……13′
所以三等品率最多为3%..............................14′
学后反思 本题主要考查学生运用知识,迁移知识的能力.解决该类实际问题的关键是将实际问题化为数学问题,利用已学的知识进行处理,这也是今后高考的一大热点.
