数学人教A版选修2-3 超几何分布和二项分布的比较(19张PPT)
文档属性
| 名称 | 数学人教A版选修2-3 超几何分布和二项分布的比较(19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 10.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-27 00:00:00 | ||
图片预览



文档简介
超几何分布与二项分布的比较
2.常见的离散型随机变量的分布
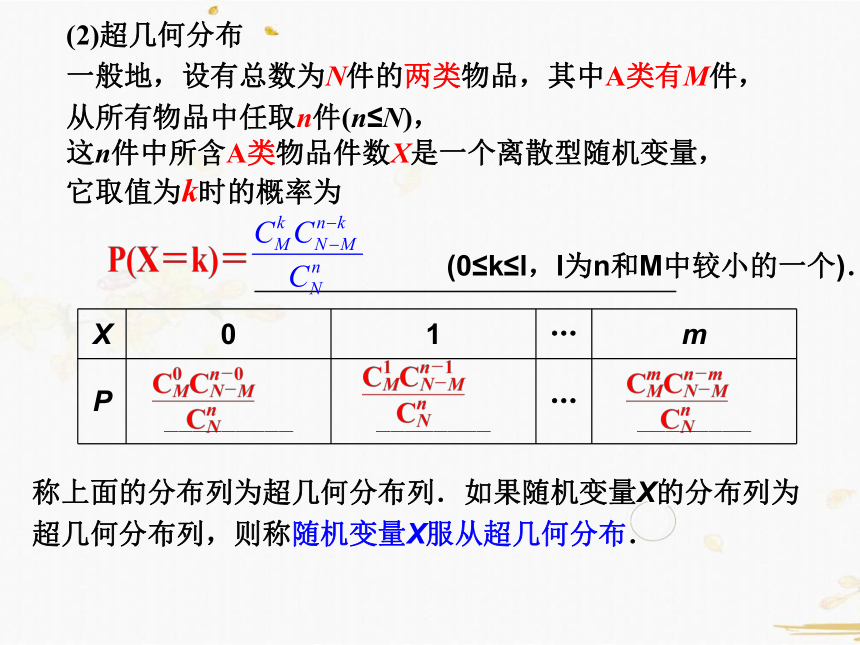
(2)超几何分布
一般地,设有总数为N件的两类物品,其中A类有M件,
从所有物品中任取n件(n≤N),
这n件中所含A类物品件数X是一个离散型随机变量,
它取值为k时的概率为
称上面的分布列为超几何分布列.如果随机变量X的分布列为
超几何分布列,则称随机变量X服从超几何分布.
X
0
1
…
m
P
_________
________
…
________
(0≤k≤l,l为n和M中较小的一个).
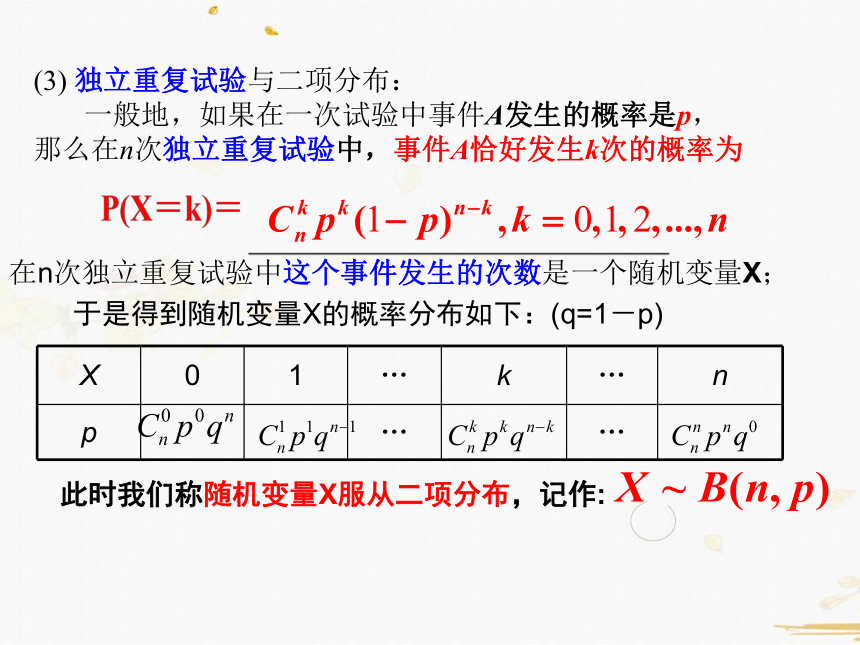
(3) 独立重复试验与二项分布:
一般地,如果在一次试验中事件A发生的概率是p,
那么在n次独立重复试验中,事件A恰好发生k次的概率为
此时我们称随机变量X服从二项分布,记作:
X
0
1
…
k
…
n
p
…
…
于是得到随机变量X的概率分布如下:(q=1-p)
在n次独立重复试验中这个事件发生的次数是一个随机变量X;
【分析】需要认真体会题目的情境,究竟随机变量符合哪种分布.
(1)有放回抽样时,取到黑球的个数X的分布列;
(2)不放回抽样时,取到黑球的个数Y的分布列.
袋中有3个白球、2个黑球,从中随机地连续抽取3次,每次取1个球.求:
(1)答案
(2)答案
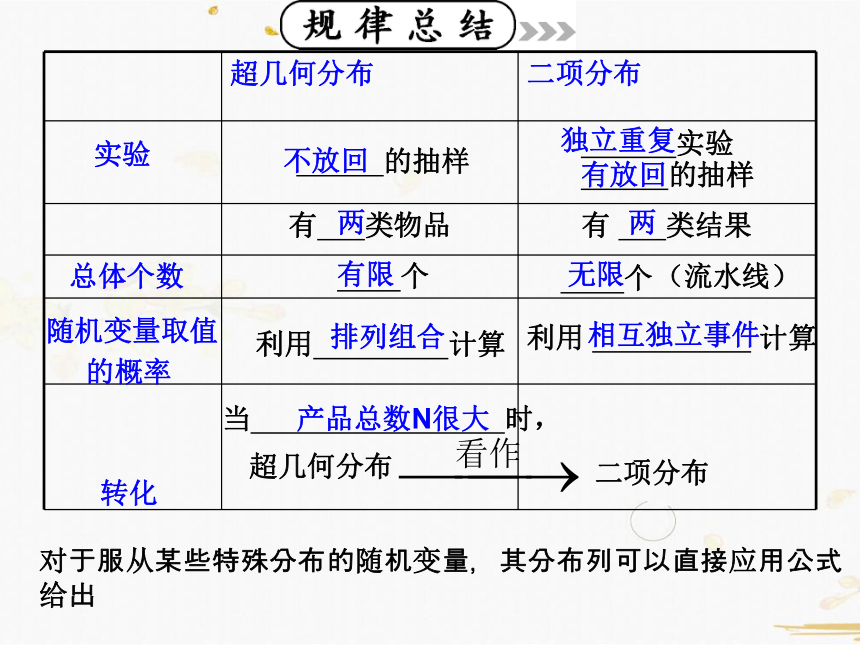
超几何分布
二项分布
有 类物品
有 类结果
的抽样
实验
个
个
(流水线)
利用 计算
利用 计算
当 时,
超几何分布
二项分布
实验
总体个数
随机变量取值
的概率
转化
对于服从某些特殊分布的随机变量,其分布列可以直接应用公式给出
不放回
的抽样
有放回
独立重复
排列组合
相互独立事件
有限
无限
产品总数N很大
两
两
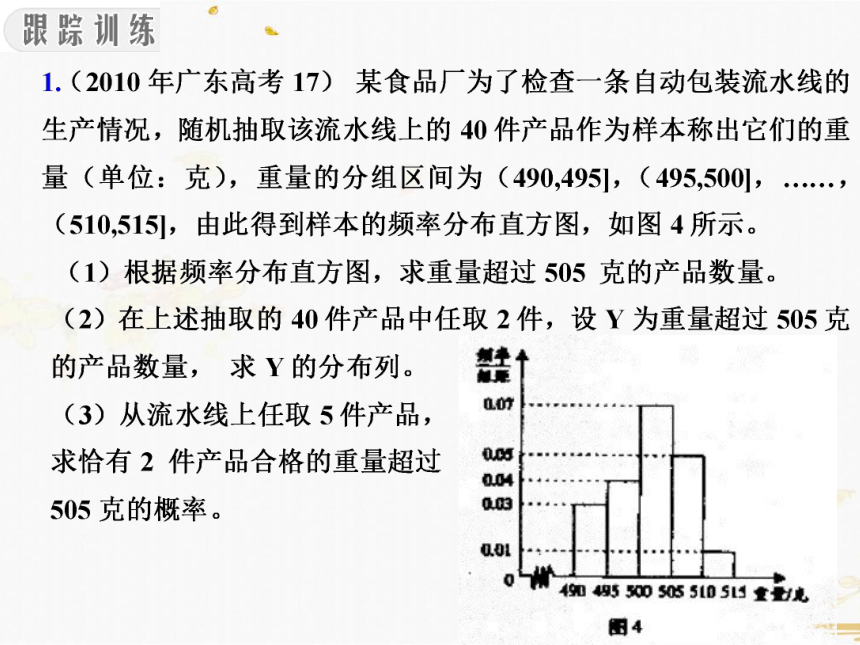
(3)利用样本估计总体,该流水线上产品重量超过505克的概率为0.3,
设任取的5件产品中重量超过505克的产品数量X,则X服从二项分布,
故所求概率为P(X=2)=C52(0.3)2(0.7)3=0.3087
总结
(Ⅱ)由于从40位学生中任意抽取3位的结果数为C403,
其中具有听觉记忆能力或视觉记忆能力偏高或超常的学生共24人,
4.袋中装着标有数字1,2,3的小球各2个,从袋中任取2个小球,每个小球被取出的可能性都相等.
(1)求取出的2个小球上的数字互不相同的概率;
(2)用ξ表示取出的2个小球上的数字之和,求随机变量ξ的概率分布.
解:法(1)记“取出的2个小球上的数字互不相同”为事件A
法(2)记“取出的2个小球上的数字互不相同”为事件A,
“取出的2个小球上的数字相同”的事件记为B,
则事件A与事件B是对立事件
∵从袋中的6个小球中任取2个小球的方法共有C62
其中取出的2个小球上的数字互不相同的方法有C32 C21 C21
∴
P
(
)
A
=
C
2
3
C
1
2
C
1
2
C
2
6
=
3
×
2
×
2
3
×
5
=
4
5
总结
(1)求该校报考飞行员的总人数;
(2)以这所学校的样本数据来估计全省的总体数据,若从全省报考飞行员的学生中(人数很多)任选3人,设X表示体重超过60kg的学生人数,求X的分布列和数学期望.
5.为了了解今年某校高三毕业班准备报考飞行员学生的体身素质,学校对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
[分析] 先由频率直方图中前三组频率的比及第2小组频数及频率分布直方图的性质求出n的值和任取一个报考学生体重超过60kg的概率.再由从报考飞行员的学生中任选3人知,这是三次独立重复试验,故X服从二项分布.
【解析】(1)有放回抽样时,取到的黑球数X可能的取值为0,1,2,3.
因此,X的分布列为:
X
0
1
2
3
P
?
?
?
?
(1)有放回抽样时,取到黑球的个数X的分布列;
每次发生概率一样
袋中有3个白球、2个黑球,从中随机地连续抽取3次,每次取1个球.求:
(2)不放回抽样时,取到黑球的个数Y的分布列.
解(2)不放回抽样时,取到的黑球数Y可能的取值为0,1,2,且有:
因此,Y的分布列为:
Y
0
1
2
P
?
?
?
袋中有3个白球、2个黑球,从中随机地连续抽取3次,每次取1个球.求:
2.常见的离散型随机变量的分布
(2)超几何分布
一般地,设有总数为N件的两类物品,其中A类有M件,
从所有物品中任取n件(n≤N),
这n件中所含A类物品件数X是一个离散型随机变量,
它取值为k时的概率为
称上面的分布列为超几何分布列.如果随机变量X的分布列为
超几何分布列,则称随机变量X服从超几何分布.
X
0
1
…
m
P
_________
________
…
________
(0≤k≤l,l为n和M中较小的一个).
(3) 独立重复试验与二项分布:
一般地,如果在一次试验中事件A发生的概率是p,
那么在n次独立重复试验中,事件A恰好发生k次的概率为
此时我们称随机变量X服从二项分布,记作:
X
0
1
…
k
…
n
p
…
…
于是得到随机变量X的概率分布如下:(q=1-p)
在n次独立重复试验中这个事件发生的次数是一个随机变量X;
【分析】需要认真体会题目的情境,究竟随机变量符合哪种分布.
(1)有放回抽样时,取到黑球的个数X的分布列;
(2)不放回抽样时,取到黑球的个数Y的分布列.
袋中有3个白球、2个黑球,从中随机地连续抽取3次,每次取1个球.求:
(1)答案
(2)答案
超几何分布
二项分布
有 类物品
有 类结果
的抽样
实验
个
个
(流水线)
利用 计算
利用 计算
当 时,
超几何分布
二项分布
实验
总体个数
随机变量取值
的概率
转化
对于服从某些特殊分布的随机变量,其分布列可以直接应用公式给出
不放回
的抽样
有放回
独立重复
排列组合
相互独立事件
有限
无限
产品总数N很大
两
两
(3)利用样本估计总体,该流水线上产品重量超过505克的概率为0.3,
设任取的5件产品中重量超过505克的产品数量X,则X服从二项分布,
故所求概率为P(X=2)=C52(0.3)2(0.7)3=0.3087
总结
(Ⅱ)由于从40位学生中任意抽取3位的结果数为C403,
其中具有听觉记忆能力或视觉记忆能力偏高或超常的学生共24人,
4.袋中装着标有数字1,2,3的小球各2个,从袋中任取2个小球,每个小球被取出的可能性都相等.
(1)求取出的2个小球上的数字互不相同的概率;
(2)用ξ表示取出的2个小球上的数字之和,求随机变量ξ的概率分布.
解:法(1)记“取出的2个小球上的数字互不相同”为事件A
法(2)记“取出的2个小球上的数字互不相同”为事件A,
“取出的2个小球上的数字相同”的事件记为B,
则事件A与事件B是对立事件
∵从袋中的6个小球中任取2个小球的方法共有C62
其中取出的2个小球上的数字互不相同的方法有C32 C21 C21
∴
P
(
)
A
=
C
2
3
C
1
2
C
1
2
C
2
6
=
3
×
2
×
2
3
×
5
=
4
5
总结
(1)求该校报考飞行员的总人数;
(2)以这所学校的样本数据来估计全省的总体数据,若从全省报考飞行员的学生中(人数很多)任选3人,设X表示体重超过60kg的学生人数,求X的分布列和数学期望.
5.为了了解今年某校高三毕业班准备报考飞行员学生的体身素质,学校对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
[分析] 先由频率直方图中前三组频率的比及第2小组频数及频率分布直方图的性质求出n的值和任取一个报考学生体重超过60kg的概率.再由从报考飞行员的学生中任选3人知,这是三次独立重复试验,故X服从二项分布.
【解析】(1)有放回抽样时,取到的黑球数X可能的取值为0,1,2,3.
因此,X的分布列为:
X
0
1
2
3
P
?
?
?
?
(1)有放回抽样时,取到黑球的个数X的分布列;
每次发生概率一样
袋中有3个白球、2个黑球,从中随机地连续抽取3次,每次取1个球.求:
(2)不放回抽样时,取到黑球的个数Y的分布列.
解(2)不放回抽样时,取到的黑球数Y可能的取值为0,1,2,且有:
因此,Y的分布列为:
Y
0
1
2
P
?
?
?
袋中有3个白球、2个黑球,从中随机地连续抽取3次,每次取1个球.求:
