2020--2021学年八年级下册数学人教版 第十八章 平行四边形 综合能力检测卷(word版含解析)
文档属性
| 名称 | 2020--2021学年八年级下册数学人教版 第十八章 平行四边形 综合能力检测卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 241.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-26 00:00:00 | ||
图片预览

文档简介
第十八章 综合能力检测卷
时间:60分钟
满分:100分
一、选择题(每题3分,共30分)
1.下列命题正确的是
( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角线互相垂直的四边形是菱形
C.对角线相等的四边形是矩形
D.一组邻边相等的矩形是正方形
2.如图,菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,AB边的中点,连接EF.若EF=,OC=2,则菱形ABCD的面积为
( )
A.2
B.4
C.6
D.8
第2题图
第3题图
第4题图
3.如图,在矩形ABCD中,AE平分∠BAD,交边BC于点E,若ED=5,EC=3,则矩形ABCD的周长为
( )
A.11
B.14
C.22
D.28
4.如图,平行四边形ABCD的对角线AC与BD相交于点O,
AE⊥BC,垂足为E,AB=,AC=2,BD=4,则AE的长为
( )
A.
B.
C.
D.
5.如图,在给定的一张平行四边形纸片上作一个菱形,甲、乙两人的作法如下:
甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于点M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于点E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断
( )
A.甲正确,乙错误
B.甲、乙均正确
C.乙正确,甲错误
D.甲、乙均错误
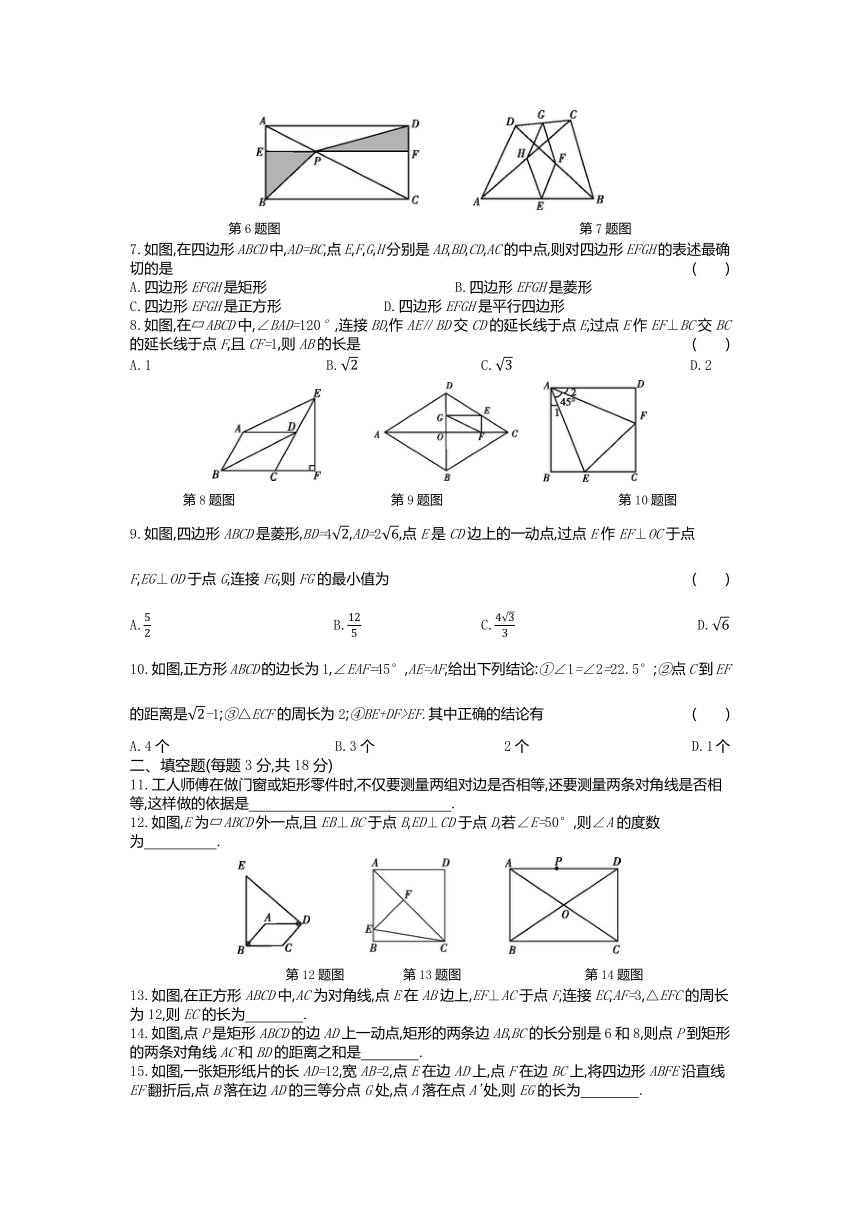
6.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于点E,F,连接PB,PD.若AE=2,PF=8.则图中阴影部分的面积为
( )
A.10
B.12
C.16
D.18
第6题图
第7题图
7.如图,在四边形ABCD中,AD=BC,点E,F,G,H分别是AB,BD,CD,AC的中点,则对四边形EFGH的表述最确切的是
( )
A.四边形EFGH是矩形
B.四边形EFGH是菱形
C.四边形EFGH是正方形
D.四边形EFGH是平行四边形
8.如图,在?ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD的延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是
( )
A.1
B.
C.
D.2
第8题图
第9题图
第10题图
9.如图,四边形ABCD是菱形,BD=4,AD=2,点E是CD边上的一动点,过点E作EF⊥OC于点F,EG⊥OD于点G,连接FG,则FG的最小值为
( )
A.
B.
C.
D.
10.如图,正方形ABCD的边长为1,∠EAF=45°,AE=AF,给出下列结论:①∠1=∠2=22.5°;②点C到EF的距离是-1;③△ECF的周长为2;④BE+DF>EF.其中正确的结论有
( )
A.4个
B.3个
2个
D.1个
二、填空题(每题3分,共18分)
11.工人师傅在做门窗或矩形零件时,不仅要测量两组对边是否相等,还要测量两条对角线是否相等,这样做的依据是 .?
12.如图,E为?ABCD外一点,且EB⊥BC于点B,ED⊥CD于点D,若∠E=50°,则∠A的度数为 .?
第12题图
第13题图
第14题图
13.如图,在正方形ABCD中,AC为对角线,点E在AB边上,EF⊥AC于点F,连接EC,AF=3,△EFC的周长为12,则EC的长为 .?
14.如图,点P是矩形ABCD的边AD上一动点,矩形的两条边AB,BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是 .?
15.如图,一张矩形纸片的长AD=12,宽AB=2,点E在边AD上,点F在边BC上,将四边形ABFE沿直线EF翻折后,点B落在边AD的三等分点G处,点A落在点A'处,则EG的长为 .?
第15题图
第16题图
16.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为 .?
三、解答题(共52分)
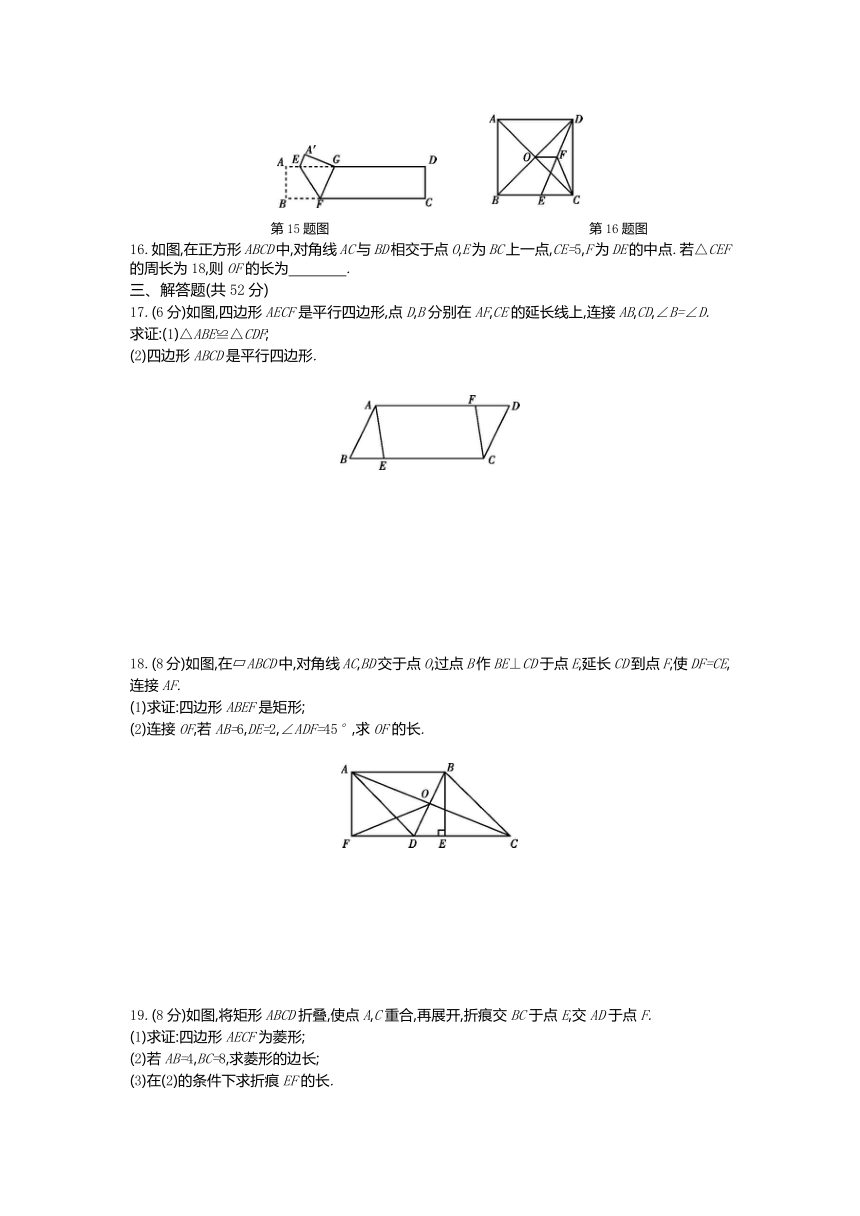
17.(6分)如图,四边形AECF是平行四边形,点D,B分别在AF,CE的延长线上,连接AB,CD,∠B=∠D.
求证:(1)△ABE≌△CDF;
(2)四边形ABCD是平行四边形.
18.(8分)如图,在?ABCD中,对角线AC,BD交于点O,过点B作BE⊥CD于点E,延长CD到点F,使DF=CE,连接AF.
(1)求证:四边形ABEF是矩形;
(2)连接OF,若AB=6,DE=2,∠ADF=45°,求OF的长.
19.(8分)如图,将矩形ABCD折叠,使点A,C重合,再展开,折痕交BC于点E,交AD于点F.
(1)求证:四边形AECF为菱形;
(2)若AB=4,BC=8,求菱形的边长;
(3)在(2)的条件下求折痕EF的长.
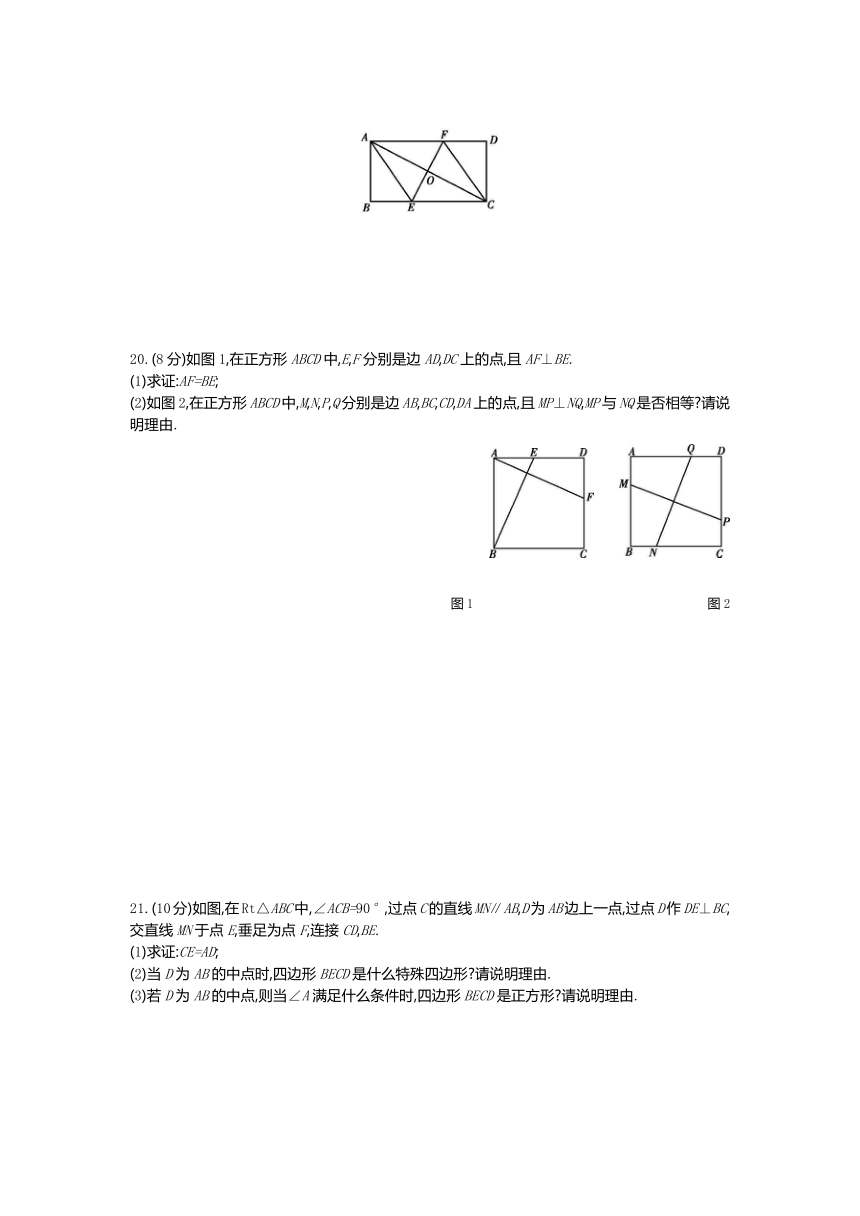
20.(8分)如图1,在正方形ABCD中,E,F分别是边AD,DC上的点,且AF⊥BE.
(1)求证:AF=BE;
(2)如图2,在正方形ABCD中,M,N,P,Q分别是边AB,BC,CD,DA上的点,且MP⊥NQ,MP与NQ是否相等?请说明理由.
图1
图2
21.(10分)如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于点E,垂足为点F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB的中点时,四边形BECD是什么特殊四边形?请说明理由.
(3)若D为AB的中点,则当∠A满足什么条件时,四边形BECD是正方形?请说明理由.
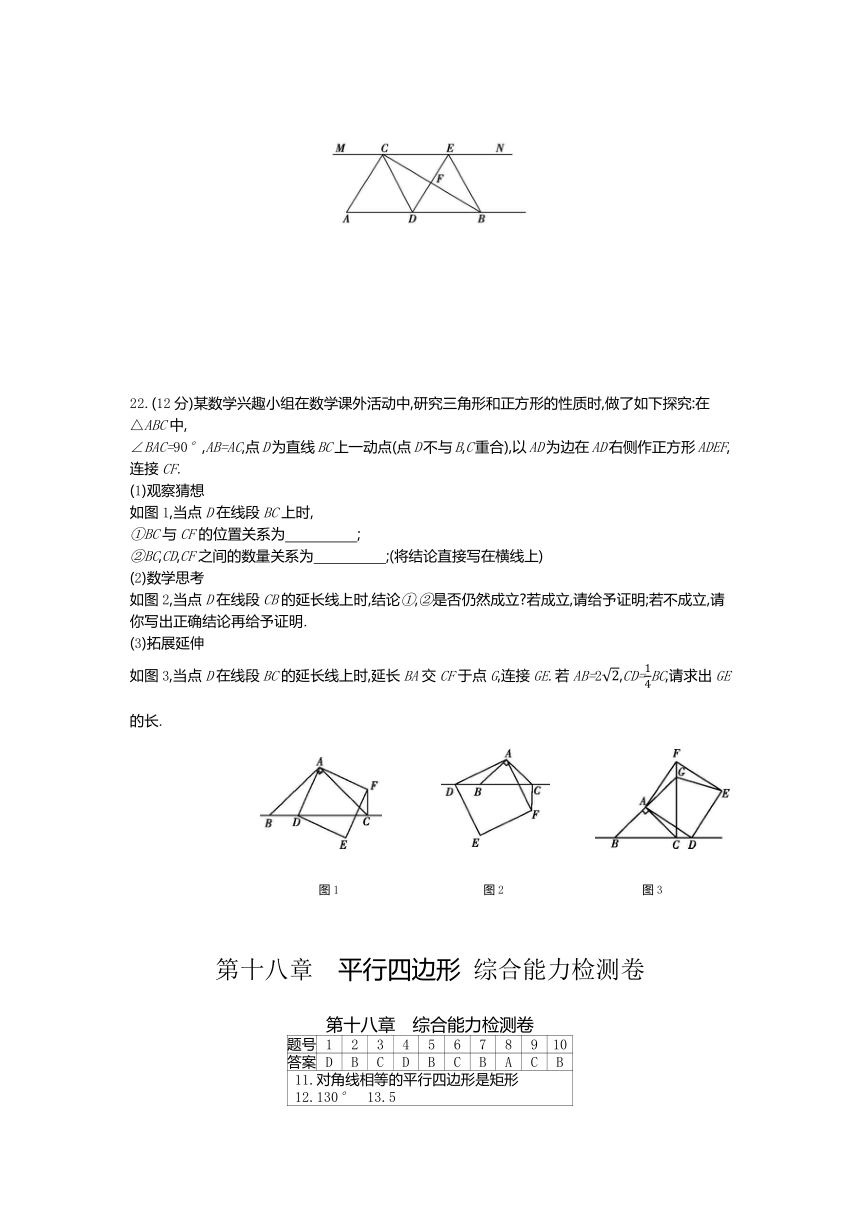
22.(12分)某数学兴趣小组在数学课外活动中,研究三角形和正方形的性质时,做了如下探究:在△ABC中,
∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为 ;?
②BC,CD,CF之间的数量关系为 ;(将结论直接写在横线上)?
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若AB=2,CD=BC,请求出GE的长.
图1
图2
图3
第十八章
平行四边形
综合能力检测卷
第十八章 综合能力检测卷
题号
1
2
3
4
5
6
7
8
9
10
答案
D
B
C
D
B
C
B
A
C
B
11.对角线相等的平行四边形是矩形 12.130° 13.5
14. 15.或 16.
1.D 【解析】 一组对边平行且相等的四边形是平行四边形,故A错误;对角线互相垂直的平行四边形是菱形,故B错误;对角线相等的平行四边形是矩形,故C错误;一组邻边相等的矩形是正方形,故D正确.故选D.
2.B 【解析】 ∵E,F分别是AD,AB边的中点,∴EF是△ABD的中位线,∴BD=2EF=2.∵四边形ABCD是菱形,∴AC=2OC=4,∴菱形ABCD的面积为AC×BD=×4×2=4.故选B.
3.C 【解析】 ∵四边形ABCD是矩形,∴∠C=90°,AD=BC,AB=CD,AD∥BC,∴∠AEB=∠DAE.∵AE平分∠BAD,∴∠BAE=∠DAE,∴∠BAE=∠AEB,∴BE=AB.∵ED=5,EC=3,∴CD===4,
∴BE=AB=CD=4,∴矩形ABCD的周长为2×(4+3+4)=22.故选C.
4.D 【解析】 ∵四边形ABCD是平行四边形,AC=2,BD=4,∴AO=1,BO=2.∵AB=,∴AO2+AB2=
BO2,∴△ABO是直角三角形且∠BAO=90°,∴BC===.∵S△ABC=AB×AC=
BC×AE,∴××2=××AE,解得AE=.故选D.
5.B 【解析】 对于甲的作法,∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAC=∠ACN.∵MN是AC的垂直平分线,∴∠AOM=∠CON=90°,AO=CO,∴△AOM≌△CON,∴MO=NO,∴四边形ANCM是平行四边形,又AC⊥MN,∴四边形ANCM是菱形,故甲的作法正确.对于乙的作法,∵四边形ABCD是平行四边形,∴AD∥BC,∴∠AFB=∠EBF,∠FAE=∠BEA.∵BF平分∠ABC,AE平∠BAD,∴∠FBE=∠FBA,
∠BAE=∠FAE,∴∠AFB=∠ABF,∠BAE=∠AEB,∴AB=AF,AB=BE,∴AF=BE.∵AF∥BE,∴四边形ABEF是平行四边形,又AB=AF,∴四边形ABEF是菱形,故乙的作法正确.故选B.
6.C 【解析】 如图,过点P作MN⊥AD于点M,交BC于点N,则四边形AEPM、四边形DFPM、四边形CFPN、四边形BEPN都是矩形,∴S△ADC=S△ABC,S△AMP=S△AEP,S△PBE=S△PBN,S△PFD=S△PDM,S△PFC=S△PCN,
∴S△PBE=S△DFP=×2×8=8,∴=8+8=16.故选C.
7.B 【解析】 ∵点E,H分别是AB,AC的中点,∴EH∥BC,EH=BC.同理,EF∥AD,EF=AD,HG∥AD,
HG=AD,∴EF∥HG,EF=HG,∴四边形EFGH是平行四边形.∵AD=BC,∴EF=EH,∴平行四边形EFGH是菱形.故选B.
8.A 【解析】 ∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∠BCD=∠BAD=120°.∵AE∥BD,
∴四边形ABDE是平行四边形,∴AB=DE,∴CE=2AB,∵∠BCD=120°,∴∠ECF=60°,∵EF⊥BF,
∴∠CEF=30°,∴CE=2CF=2,∴AB=1.故选A.
9.C 【解析】 连接OE,∵四边形ABCD是菱形,∴AD=DC,OA=OC,OB=OD,AC⊥BD.∵EF⊥OC,
EG⊥OD,∴四边形OGEF是矩形,∴OE=GF.当OE⊥DC时,OE的值最小,即GF的值最小.∵BD=4,
∴OD=2,∴OC===4.∵=OD·OC=DC·OE,∴×2×4=×2×OE,
∴OE=,∴FG的最小值为.故选C.
10.B 【解析】 ∵四边形ABCD为正方形,∴AB=AD,∠BAD=∠B=∠D=90°.在Rt△ABE和Rt△ADF中,∵AB=AD,AE=AF,∴Rt△ABE≌Rt△ADF,∴∠1=∠2.∵∠EAF=45°,∴∠1=∠2=∠22.5°,故①正确.如图,连接AC交EF于点H,∵Rt△ABE≌Rt△ADF,∴BE=DF,又BC=DC,∴CE=CF.∵AE=
AF,∴AC垂直平分EF,AH平分∠EAF,又∠1=∠2,∴AE平分∠BAC,AF平分∠DAC,∴EB=EH,FD=FH,
∴BE+DF=EH+HF=EF,故④错误.△ECF的周长为CE+CF+EF=CE+BE+CF+DF=CB+CD=
1+1=2,故③正确.设BE=x,则EF=2x,CE=1-x,∵△CEF为等腰直角三角形,∴EF=CE,∴2x=(1-x),解得x=-1,∴BE=-1.在Rt△ECF中,EH=FH,∴CH=EF=EH=BE=-1.∵CH⊥EF,∴点C到EF的距离是-1,故②正确.综上,正确的结论是①②③.故选B.
11.对角线相等的平行四边形是矩形
12.130° 【解析】 ∵EB⊥BC,ED⊥CD,∴∠EBC=90°,∠EDC=90°.∵∠E=50°,∴∠C=360°-90°-90°-50°=130°.∵四边形ABCD是平行四边形,∴∠A=∠C=130°.
13.5 【解析】 ∵四边形ABCD是正方形,∴∠BAC=45°,∵EF⊥AC,∴∠AEF=∠BAC=45°,∴EF=
AF=3.∵△EFC的周长为12,∴EF+CF+EC=12,∴CF=9-EC.在Rt△EFC中,由勾股定理,得(9-EC)2+32=EC2,解得EC=5.
14. 【解析】 如图,过点P作PE⊥AC于点E,PF⊥BD于点F,连接PO.因为AB,BC的长分别是6和8,所以AC=BD=10,所以AO=OD=5,因为S△PAO+S△POD=S△AOD,所以AO×PE+OD×PF=×6×8,所以PE+PF=,即点P到矩形的两条对角线AC和BD的距离之和是.
15.或 【解析】 过点G作GH⊥BC于点H,则四边形ABHG是矩形.∵G是AD的三等分点,∴AG=4或8.由折叠的性质,可知FG=FB,∠EFB=∠EFG.∵AD∥BC,∴∠FEG=∠EFB,∴∠FEG=∠GFE,
∴EG=FG.设EG=x,则FG=FB=x.在Rt△FGH中,∵FG2=GH2+FH2,∴x2=22+(4-x)2或x2=22+(8-x)2,∴x=或,即EG的长为或.
16. 【解析】 ∵四边形ABCD是正方形,∴BO=DO,BC=CD,∠BCD=90°.在Rt△DCE中,F为DE的中点,∴CF=DE=EF=DF.∵△CEF的周长为18,CE=5,∴CF+EF=18-5=13,∴DE=DF+EF=13.在Rt△DCE中,根据勾股定理,得DC==12,∴BC=12,∴BE=12-5=7.在△BDE中,∵BO=DO,F为DE的中点,∴OF为△BDE的中位线,∴OF=BE=.
17.【解析】 (1)∵四边形AECF是平行四边形,
∴AE=CF,AF=CE,∠AEC=∠AFC,∴∠AEB=∠CFD.
在△ABE和△CDF中,
∴△ABE≌△CDF.
(2)由(1)知△ABE≌△CDF,
∴AB=CD,BE=DF,
∵AF=CE,∴AF+DF=CE+BE,即AD=BC,
又AD∥BC,∴四边形ABCD是平行四边形.
18.【解析】 (1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵DF=CE,∴DF+DE=CE+DE,
即FE=CD,∴FE=AB,
又AB∥FE,∴四边形ABEF是平行四边形.
∵BE⊥CD,∴∠BEF=90°,
∴四边形ABEF是矩形.
(2)由(1)知四边形ABEF是矩形,∴EF=AB=6,
∵DE=2,∴DF=CE=4,∴CF=4+4+2=10.
在Rt△ADF中,∠ADF=45°,∴AF=DF=4,
在Rt△ACF中,由勾股定理,得AC===2,
∵四边形ABCD是平行四边形,∴OA=OC,
∴OF=AC=.
19.【解析】 (1)∵将矩形ABCD折叠后点A,C重合,折痕为EF,
∴OA=OC,EF⊥AC,EA=EC.
∵AD∥BC,∴∠FAC=∠ECA,
又∠AOF=∠COE,∴△AOF≌△COE,∴OF=OE.
∴四边形AECF为平行四边形,
又EF⊥AC,∴四边形AECF为菱形.
(2)设菱形的边长为x,则BE=BC-CE=8-x,AE=x.
在Rt△ABE中,∵BE2+AB2=AE2,
∴(8-x)2+42=x2,解得x=5,
即菱形的边长为5.
(3)在Rt△ABC中,AC===4,
∴OA=AC=2.
在Rt△AOE中,OE===,
∴EF=2OE=2.
20.【解析】 (1)∵四边形ABCD是正方形,
∴AB=AD,∠BAE=∠D=90°,∴∠DAF+∠BAF=90°.
∵AF⊥BE,∴∠ABE+∠BAF=90°,∴∠ABE=∠DAF.
在△ABE和△DAF中,
∴△ABE≌△DAF,∴AF=BE.
(2)MP与NQ相等.理由如下:
如图,过点A作AG∥MP交CD于点G,过点B作BH∥NQ交AD于点H.
∵MP⊥NQ,∴AG⊥BH.
∵AB∥CD,AD∥BC,
∴四边形AMPG与四边形BNQH都是平行四边形,
∴AG=PM,BH=NQ.
∵四边形ABCD为正方形,
∴AB=AD,∠BAH=∠D=90°,∴∠DAG+∠BAG=90°.
∵AG⊥BH,∴∠ABH+∠BAG=90°,∴∠ABH=∠DAG.
在△ABH和△DAG中,
∴△ABH≌△DAG,∴AG=BH,∴MP=NQ.
21.【解析】 (1)∵DE⊥BC,∴∠DFB=90°.
∵∠ACB=90°,∴∠ACB=∠DFB,∴AC∥DE.
∵MN∥AB,即CE∥AD,∴四边形ADEC是平行四边形,
∴CE=AD.
(2)四边形BECD是菱形.理由如下:
∵D为AB的中点,∴AD=BD.
由(1)知CE=AD,∴BD=CE,
∵BD∥CE,∴四边形BECD是平行四边形,
又DE⊥BC,∴四边形BECD是菱形.
(3)当∠A=45°时,四边形BECD是正方形.理由如下:
∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°,∴AC=BC.
∵D为AB的中点,∴CD⊥AB,∴∠CDB=90°,
又四边形BECD是菱形,∴四边形BECD是正方形.
即当∠A=45°时,四边形BECD是正方形.
对于特殊的平行四边形,一定要弄清各自的特征,正确区分各类特殊的平行四边形,同时又要把握好它们之间的联系.
22.【解析】 (1)①垂直;②BC=CD+CF
(2)①成立,②不成立,正确结论是BC=`DC-CF.证明如下:
∵四边形ADEF是正方形,∴AD=AF,∠DAF=90°.
∵∠BAC=90°,∴∠DAB=∠FAC,
又AD=AF,AB=AC,∴△DAB≌△FAC.
∴DB=CF,∠DBA=∠FCA.
∵∠BAC=90°,AB=AC,∴∠ABC=∠ACB=45°.
∴∠FCA=∠DBA=135°,∴∠BCF=90°,∴BC⊥CF.
∵BC=DC-DB,DB=CF,∴BC=DC-CF.
(3)如图,过点A作AM⊥BC于点M,过点E作EN⊥BC于点N,EP⊥CF于点P.易得四边形PCNE为矩形,
∵∠BAC=90°,AB=AC=2,
∴BC=4,AM=BM=CM=2.
∵CD=BC,∴CD=1,∴MD=3.
∵∠ADC+∠EDN=90°,∠EDN+∠DEN=90°,
∴∠ADC=∠DEN,
又∠AMD=∠DNE=90°,AD=DE,
∴△AMD≌△DNE,∴DN=AM=2,EN=MD=3.
∵CG=BC=4,∴GP=4-3=1.
在Rt△GPE中,由勾股定理,得GE===.
对于线段之间关系的猜想题,一般要考虑两种情况:一是位置关系,即平行或垂直;二是数量关系,即相等或倍数关系,若是三条线段,一般存在三者间的和差关系.本题是探究型问题,解题时应对题目中变化的条件进行分析,把握原有图形的特点,探究变化条件的特点,借用类比思想逐步解题.
时间:60分钟
满分:100分
一、选择题(每题3分,共30分)
1.下列命题正确的是
( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角线互相垂直的四边形是菱形
C.对角线相等的四边形是矩形
D.一组邻边相等的矩形是正方形
2.如图,菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,AB边的中点,连接EF.若EF=,OC=2,则菱形ABCD的面积为
( )
A.2
B.4
C.6
D.8
第2题图
第3题图
第4题图
3.如图,在矩形ABCD中,AE平分∠BAD,交边BC于点E,若ED=5,EC=3,则矩形ABCD的周长为
( )
A.11
B.14
C.22
D.28
4.如图,平行四边形ABCD的对角线AC与BD相交于点O,
AE⊥BC,垂足为E,AB=,AC=2,BD=4,则AE的长为
( )
A.
B.
C.
D.
5.如图,在给定的一张平行四边形纸片上作一个菱形,甲、乙两人的作法如下:
甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于点M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于点E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断
( )
A.甲正确,乙错误
B.甲、乙均正确
C.乙正确,甲错误
D.甲、乙均错误
6.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于点E,F,连接PB,PD.若AE=2,PF=8.则图中阴影部分的面积为
( )
A.10
B.12
C.16
D.18
第6题图
第7题图
7.如图,在四边形ABCD中,AD=BC,点E,F,G,H分别是AB,BD,CD,AC的中点,则对四边形EFGH的表述最确切的是
( )
A.四边形EFGH是矩形
B.四边形EFGH是菱形
C.四边形EFGH是正方形
D.四边形EFGH是平行四边形
8.如图,在?ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD的延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是
( )
A.1
B.
C.
D.2
第8题图
第9题图
第10题图
9.如图,四边形ABCD是菱形,BD=4,AD=2,点E是CD边上的一动点,过点E作EF⊥OC于点F,EG⊥OD于点G,连接FG,则FG的最小值为
( )
A.
B.
C.
D.
10.如图,正方形ABCD的边长为1,∠EAF=45°,AE=AF,给出下列结论:①∠1=∠2=22.5°;②点C到EF的距离是-1;③△ECF的周长为2;④BE+DF>EF.其中正确的结论有
( )
A.4个
B.3个
2个
D.1个
二、填空题(每题3分,共18分)
11.工人师傅在做门窗或矩形零件时,不仅要测量两组对边是否相等,还要测量两条对角线是否相等,这样做的依据是 .?
12.如图,E为?ABCD外一点,且EB⊥BC于点B,ED⊥CD于点D,若∠E=50°,则∠A的度数为 .?
第12题图
第13题图
第14题图
13.如图,在正方形ABCD中,AC为对角线,点E在AB边上,EF⊥AC于点F,连接EC,AF=3,△EFC的周长为12,则EC的长为 .?
14.如图,点P是矩形ABCD的边AD上一动点,矩形的两条边AB,BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是 .?
15.如图,一张矩形纸片的长AD=12,宽AB=2,点E在边AD上,点F在边BC上,将四边形ABFE沿直线EF翻折后,点B落在边AD的三等分点G处,点A落在点A'处,则EG的长为 .?
第15题图
第16题图
16.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为 .?
三、解答题(共52分)
17.(6分)如图,四边形AECF是平行四边形,点D,B分别在AF,CE的延长线上,连接AB,CD,∠B=∠D.
求证:(1)△ABE≌△CDF;
(2)四边形ABCD是平行四边形.
18.(8分)如图,在?ABCD中,对角线AC,BD交于点O,过点B作BE⊥CD于点E,延长CD到点F,使DF=CE,连接AF.
(1)求证:四边形ABEF是矩形;
(2)连接OF,若AB=6,DE=2,∠ADF=45°,求OF的长.
19.(8分)如图,将矩形ABCD折叠,使点A,C重合,再展开,折痕交BC于点E,交AD于点F.
(1)求证:四边形AECF为菱形;
(2)若AB=4,BC=8,求菱形的边长;
(3)在(2)的条件下求折痕EF的长.
20.(8分)如图1,在正方形ABCD中,E,F分别是边AD,DC上的点,且AF⊥BE.
(1)求证:AF=BE;
(2)如图2,在正方形ABCD中,M,N,P,Q分别是边AB,BC,CD,DA上的点,且MP⊥NQ,MP与NQ是否相等?请说明理由.
图1
图2
21.(10分)如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于点E,垂足为点F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB的中点时,四边形BECD是什么特殊四边形?请说明理由.
(3)若D为AB的中点,则当∠A满足什么条件时,四边形BECD是正方形?请说明理由.
22.(12分)某数学兴趣小组在数学课外活动中,研究三角形和正方形的性质时,做了如下探究:在△ABC中,
∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为 ;?
②BC,CD,CF之间的数量关系为 ;(将结论直接写在横线上)?
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若AB=2,CD=BC,请求出GE的长.
图1
图2
图3
第十八章
平行四边形
综合能力检测卷
第十八章 综合能力检测卷
题号
1
2
3
4
5
6
7
8
9
10
答案
D
B
C
D
B
C
B
A
C
B
11.对角线相等的平行四边形是矩形 12.130° 13.5
14. 15.或 16.
1.D 【解析】 一组对边平行且相等的四边形是平行四边形,故A错误;对角线互相垂直的平行四边形是菱形,故B错误;对角线相等的平行四边形是矩形,故C错误;一组邻边相等的矩形是正方形,故D正确.故选D.
2.B 【解析】 ∵E,F分别是AD,AB边的中点,∴EF是△ABD的中位线,∴BD=2EF=2.∵四边形ABCD是菱形,∴AC=2OC=4,∴菱形ABCD的面积为AC×BD=×4×2=4.故选B.
3.C 【解析】 ∵四边形ABCD是矩形,∴∠C=90°,AD=BC,AB=CD,AD∥BC,∴∠AEB=∠DAE.∵AE平分∠BAD,∴∠BAE=∠DAE,∴∠BAE=∠AEB,∴BE=AB.∵ED=5,EC=3,∴CD===4,
∴BE=AB=CD=4,∴矩形ABCD的周长为2×(4+3+4)=22.故选C.
4.D 【解析】 ∵四边形ABCD是平行四边形,AC=2,BD=4,∴AO=1,BO=2.∵AB=,∴AO2+AB2=
BO2,∴△ABO是直角三角形且∠BAO=90°,∴BC===.∵S△ABC=AB×AC=
BC×AE,∴××2=××AE,解得AE=.故选D.
5.B 【解析】 对于甲的作法,∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAC=∠ACN.∵MN是AC的垂直平分线,∴∠AOM=∠CON=90°,AO=CO,∴△AOM≌△CON,∴MO=NO,∴四边形ANCM是平行四边形,又AC⊥MN,∴四边形ANCM是菱形,故甲的作法正确.对于乙的作法,∵四边形ABCD是平行四边形,∴AD∥BC,∴∠AFB=∠EBF,∠FAE=∠BEA.∵BF平分∠ABC,AE平∠BAD,∴∠FBE=∠FBA,
∠BAE=∠FAE,∴∠AFB=∠ABF,∠BAE=∠AEB,∴AB=AF,AB=BE,∴AF=BE.∵AF∥BE,∴四边形ABEF是平行四边形,又AB=AF,∴四边形ABEF是菱形,故乙的作法正确.故选B.
6.C 【解析】 如图,过点P作MN⊥AD于点M,交BC于点N,则四边形AEPM、四边形DFPM、四边形CFPN、四边形BEPN都是矩形,∴S△ADC=S△ABC,S△AMP=S△AEP,S△PBE=S△PBN,S△PFD=S△PDM,S△PFC=S△PCN,
∴S△PBE=S△DFP=×2×8=8,∴=8+8=16.故选C.
7.B 【解析】 ∵点E,H分别是AB,AC的中点,∴EH∥BC,EH=BC.同理,EF∥AD,EF=AD,HG∥AD,
HG=AD,∴EF∥HG,EF=HG,∴四边形EFGH是平行四边形.∵AD=BC,∴EF=EH,∴平行四边形EFGH是菱形.故选B.
8.A 【解析】 ∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∠BCD=∠BAD=120°.∵AE∥BD,
∴四边形ABDE是平行四边形,∴AB=DE,∴CE=2AB,∵∠BCD=120°,∴∠ECF=60°,∵EF⊥BF,
∴∠CEF=30°,∴CE=2CF=2,∴AB=1.故选A.
9.C 【解析】 连接OE,∵四边形ABCD是菱形,∴AD=DC,OA=OC,OB=OD,AC⊥BD.∵EF⊥OC,
EG⊥OD,∴四边形OGEF是矩形,∴OE=GF.当OE⊥DC时,OE的值最小,即GF的值最小.∵BD=4,
∴OD=2,∴OC===4.∵=OD·OC=DC·OE,∴×2×4=×2×OE,
∴OE=,∴FG的最小值为.故选C.
10.B 【解析】 ∵四边形ABCD为正方形,∴AB=AD,∠BAD=∠B=∠D=90°.在Rt△ABE和Rt△ADF中,∵AB=AD,AE=AF,∴Rt△ABE≌Rt△ADF,∴∠1=∠2.∵∠EAF=45°,∴∠1=∠2=∠22.5°,故①正确.如图,连接AC交EF于点H,∵Rt△ABE≌Rt△ADF,∴BE=DF,又BC=DC,∴CE=CF.∵AE=
AF,∴AC垂直平分EF,AH平分∠EAF,又∠1=∠2,∴AE平分∠BAC,AF平分∠DAC,∴EB=EH,FD=FH,
∴BE+DF=EH+HF=EF,故④错误.△ECF的周长为CE+CF+EF=CE+BE+CF+DF=CB+CD=
1+1=2,故③正确.设BE=x,则EF=2x,CE=1-x,∵△CEF为等腰直角三角形,∴EF=CE,∴2x=(1-x),解得x=-1,∴BE=-1.在Rt△ECF中,EH=FH,∴CH=EF=EH=BE=-1.∵CH⊥EF,∴点C到EF的距离是-1,故②正确.综上,正确的结论是①②③.故选B.
11.对角线相等的平行四边形是矩形
12.130° 【解析】 ∵EB⊥BC,ED⊥CD,∴∠EBC=90°,∠EDC=90°.∵∠E=50°,∴∠C=360°-90°-90°-50°=130°.∵四边形ABCD是平行四边形,∴∠A=∠C=130°.
13.5 【解析】 ∵四边形ABCD是正方形,∴∠BAC=45°,∵EF⊥AC,∴∠AEF=∠BAC=45°,∴EF=
AF=3.∵△EFC的周长为12,∴EF+CF+EC=12,∴CF=9-EC.在Rt△EFC中,由勾股定理,得(9-EC)2+32=EC2,解得EC=5.
14. 【解析】 如图,过点P作PE⊥AC于点E,PF⊥BD于点F,连接PO.因为AB,BC的长分别是6和8,所以AC=BD=10,所以AO=OD=5,因为S△PAO+S△POD=S△AOD,所以AO×PE+OD×PF=×6×8,所以PE+PF=,即点P到矩形的两条对角线AC和BD的距离之和是.
15.或 【解析】 过点G作GH⊥BC于点H,则四边形ABHG是矩形.∵G是AD的三等分点,∴AG=4或8.由折叠的性质,可知FG=FB,∠EFB=∠EFG.∵AD∥BC,∴∠FEG=∠EFB,∴∠FEG=∠GFE,
∴EG=FG.设EG=x,则FG=FB=x.在Rt△FGH中,∵FG2=GH2+FH2,∴x2=22+(4-x)2或x2=22+(8-x)2,∴x=或,即EG的长为或.
16. 【解析】 ∵四边形ABCD是正方形,∴BO=DO,BC=CD,∠BCD=90°.在Rt△DCE中,F为DE的中点,∴CF=DE=EF=DF.∵△CEF的周长为18,CE=5,∴CF+EF=18-5=13,∴DE=DF+EF=13.在Rt△DCE中,根据勾股定理,得DC==12,∴BC=12,∴BE=12-5=7.在△BDE中,∵BO=DO,F为DE的中点,∴OF为△BDE的中位线,∴OF=BE=.
17.【解析】 (1)∵四边形AECF是平行四边形,
∴AE=CF,AF=CE,∠AEC=∠AFC,∴∠AEB=∠CFD.
在△ABE和△CDF中,
∴△ABE≌△CDF.
(2)由(1)知△ABE≌△CDF,
∴AB=CD,BE=DF,
∵AF=CE,∴AF+DF=CE+BE,即AD=BC,
又AD∥BC,∴四边形ABCD是平行四边形.
18.【解析】 (1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵DF=CE,∴DF+DE=CE+DE,
即FE=CD,∴FE=AB,
又AB∥FE,∴四边形ABEF是平行四边形.
∵BE⊥CD,∴∠BEF=90°,
∴四边形ABEF是矩形.
(2)由(1)知四边形ABEF是矩形,∴EF=AB=6,
∵DE=2,∴DF=CE=4,∴CF=4+4+2=10.
在Rt△ADF中,∠ADF=45°,∴AF=DF=4,
在Rt△ACF中,由勾股定理,得AC===2,
∵四边形ABCD是平行四边形,∴OA=OC,
∴OF=AC=.
19.【解析】 (1)∵将矩形ABCD折叠后点A,C重合,折痕为EF,
∴OA=OC,EF⊥AC,EA=EC.
∵AD∥BC,∴∠FAC=∠ECA,
又∠AOF=∠COE,∴△AOF≌△COE,∴OF=OE.
∴四边形AECF为平行四边形,
又EF⊥AC,∴四边形AECF为菱形.
(2)设菱形的边长为x,则BE=BC-CE=8-x,AE=x.
在Rt△ABE中,∵BE2+AB2=AE2,
∴(8-x)2+42=x2,解得x=5,
即菱形的边长为5.
(3)在Rt△ABC中,AC===4,
∴OA=AC=2.
在Rt△AOE中,OE===,
∴EF=2OE=2.
20.【解析】 (1)∵四边形ABCD是正方形,
∴AB=AD,∠BAE=∠D=90°,∴∠DAF+∠BAF=90°.
∵AF⊥BE,∴∠ABE+∠BAF=90°,∴∠ABE=∠DAF.
在△ABE和△DAF中,
∴△ABE≌△DAF,∴AF=BE.
(2)MP与NQ相等.理由如下:
如图,过点A作AG∥MP交CD于点G,过点B作BH∥NQ交AD于点H.
∵MP⊥NQ,∴AG⊥BH.
∵AB∥CD,AD∥BC,
∴四边形AMPG与四边形BNQH都是平行四边形,
∴AG=PM,BH=NQ.
∵四边形ABCD为正方形,
∴AB=AD,∠BAH=∠D=90°,∴∠DAG+∠BAG=90°.
∵AG⊥BH,∴∠ABH+∠BAG=90°,∴∠ABH=∠DAG.
在△ABH和△DAG中,
∴△ABH≌△DAG,∴AG=BH,∴MP=NQ.
21.【解析】 (1)∵DE⊥BC,∴∠DFB=90°.
∵∠ACB=90°,∴∠ACB=∠DFB,∴AC∥DE.
∵MN∥AB,即CE∥AD,∴四边形ADEC是平行四边形,
∴CE=AD.
(2)四边形BECD是菱形.理由如下:
∵D为AB的中点,∴AD=BD.
由(1)知CE=AD,∴BD=CE,
∵BD∥CE,∴四边形BECD是平行四边形,
又DE⊥BC,∴四边形BECD是菱形.
(3)当∠A=45°时,四边形BECD是正方形.理由如下:
∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°,∴AC=BC.
∵D为AB的中点,∴CD⊥AB,∴∠CDB=90°,
又四边形BECD是菱形,∴四边形BECD是正方形.
即当∠A=45°时,四边形BECD是正方形.
对于特殊的平行四边形,一定要弄清各自的特征,正确区分各类特殊的平行四边形,同时又要把握好它们之间的联系.
22.【解析】 (1)①垂直;②BC=CD+CF
(2)①成立,②不成立,正确结论是BC=`DC-CF.证明如下:
∵四边形ADEF是正方形,∴AD=AF,∠DAF=90°.
∵∠BAC=90°,∴∠DAB=∠FAC,
又AD=AF,AB=AC,∴△DAB≌△FAC.
∴DB=CF,∠DBA=∠FCA.
∵∠BAC=90°,AB=AC,∴∠ABC=∠ACB=45°.
∴∠FCA=∠DBA=135°,∴∠BCF=90°,∴BC⊥CF.
∵BC=DC-DB,DB=CF,∴BC=DC-CF.
(3)如图,过点A作AM⊥BC于点M,过点E作EN⊥BC于点N,EP⊥CF于点P.易得四边形PCNE为矩形,
∵∠BAC=90°,AB=AC=2,
∴BC=4,AM=BM=CM=2.
∵CD=BC,∴CD=1,∴MD=3.
∵∠ADC+∠EDN=90°,∠EDN+∠DEN=90°,
∴∠ADC=∠DEN,
又∠AMD=∠DNE=90°,AD=DE,
∴△AMD≌△DNE,∴DN=AM=2,EN=MD=3.
∵CG=BC=4,∴GP=4-3=1.
在Rt△GPE中,由勾股定理,得GE===.
对于线段之间关系的猜想题,一般要考虑两种情况:一是位置关系,即平行或垂直;二是数量关系,即相等或倍数关系,若是三条线段,一般存在三者间的和差关系.本题是探究型问题,解题时应对题目中变化的条件进行分析,把握原有图形的特点,探究变化条件的特点,借用类比思想逐步解题.
