2020—2021学年人教版九年级数学下册 第二十七章 相似 综合训练题(Word 含答案)
文档属性
| 名称 | 2020—2021学年人教版九年级数学下册 第二十七章 相似 综合训练题(Word 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 490.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-27 00:24:22 | ||
图片预览

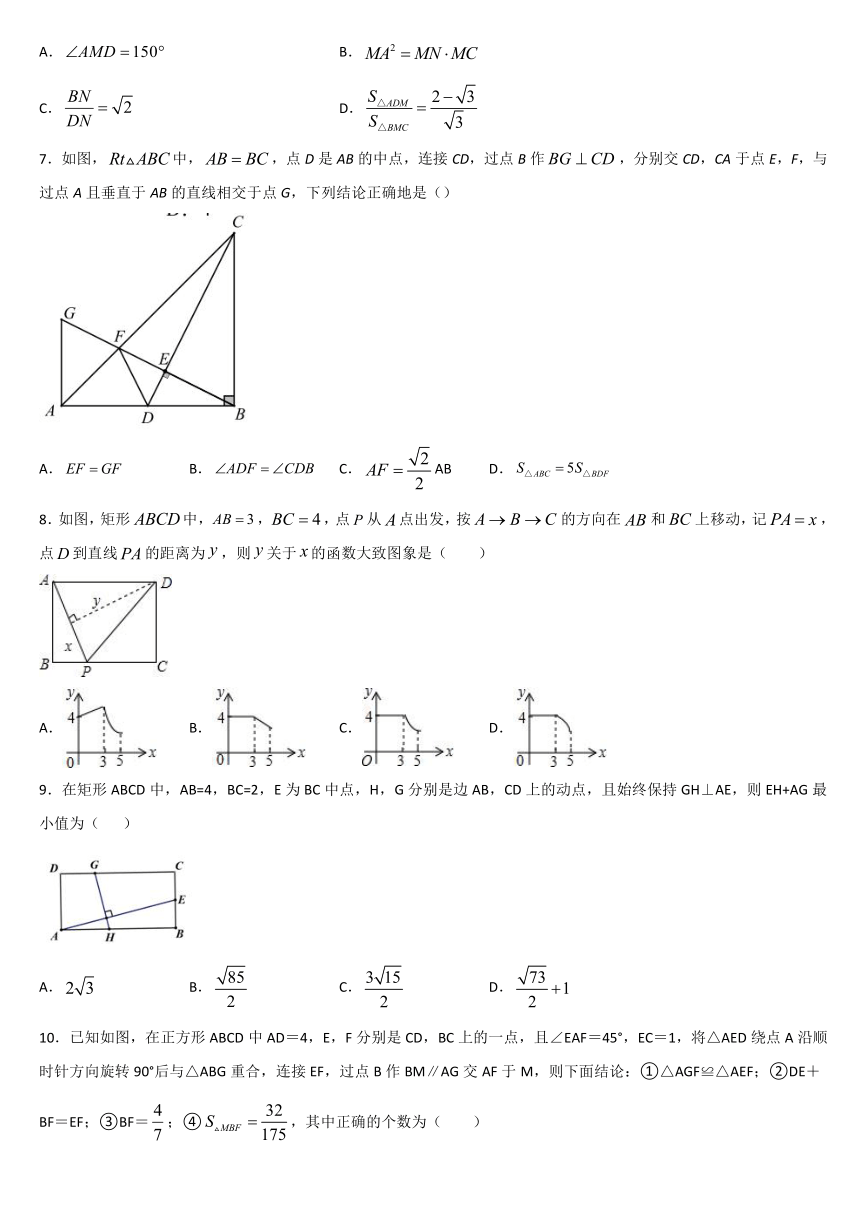
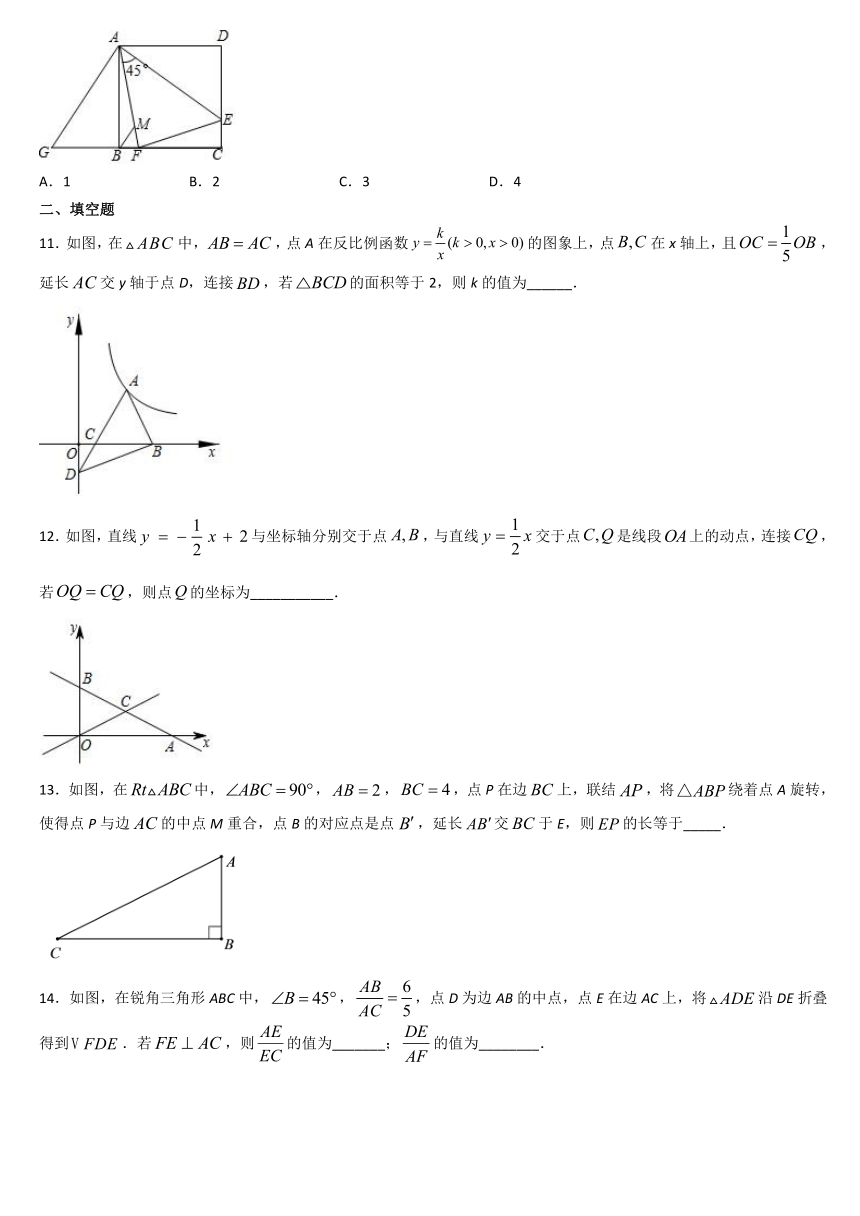
文档简介
人教版九年级数学下册
第二十七章
相似
综合训练题4
一、选择题
1.在中,,,的角平分线交于点D,则的长为(
)
A.5
B.
C.
D.
2.已知点是线段的黄金分割点,,则的值为(
)
A.
B.
C.0.618
D.
3.如图,中,于点,下列条件中不能判定是直角三角形的是(
)
A.
B.
C.
D.
4.如图,,若,则的值是(
)
A.2
B.
C.
D.3
5.如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为2米,旗杆底部与平面镜的水平距离为16米,若小明的眼睛与地面距离为1.5米,则旗杆的高度为(
)
A.米
B.12米
C.9米
D.米
6.如图,点M是正方形ABCD内一点,△MBC是等边三角形,连接AM、MD.对角线BD交CM于点N,现有以下结论不正确的是(
)
A.
B.
C.
D.
7.如图,中,,点D是AB的中点,连接CD,过点B作,分别交CD,CA于点E,F,与过点A且垂直于AB的直线相交于点G,下列结论正确地是()
A.
B.
C.AB
D.
8.如图,矩形中,,,点从点出发,按的方向在和上移动,记,点到直线的距离为,则关于的函数大致图象是(
)
A.
B.
C.
D.
9.在矩形ABCD中,AB=4,BC=2,E为BC中点,H,G分别是边AB,CD上的动点,且始终保持GH⊥AE,则EH+AG最小值为(
)
A.
B.
C.
D.
10.已知如图,在正方形ABCD中AD=4,E,F分别是CD,BC上的一点,且∠EAF=45°,EC=1,将△AED绕点A沿顺时针方向旋转90°后与△ABG重合,连接EF,过点B作BM∥AG交AF于M,则下面结论:①△AGF≌△AEF;②DE+BF=EF;③BF=;④,其中正确的个数为(
)
A.1
B.2
C.3
D.4
二、填空题
11.如图,在中,,点A在反比例函数的图象上,点在x轴上,且,延长交y轴于点D,连接,若的面积等于2,则k的值为______.
12.如图,直线与坐标轴分别交于点,与直线交于点是线段上的动点,连接,若,则点的坐标为___________.
13.如图,在中,,,,点P在边上,联结,将绕着点A旋转,使得点P与边的中点M重合,点B的对应点是点,延长交于E,则的长等于_____.
14.如图,在锐角三角形ABC中,,,点D为边AB的中点,点E在边AC上,将沿DE折叠得到.若,则的值为_______;的值为________.
15.如图,在菱形中,,点在边上,且,动点从点出发,沿着运动到点停止,过点作交菱形的边于点,若线段的中点为.当点与点重合时,的长为____,点从点运动到点的过程中,点的运动路线长为____.
三、解答题
16.如图,二次函数的图象与x轴交于点,,与y轴交于点C,抛物线的顶点为D,其对称轴与线段BC交于点E.垂直于x轴的动直线l分别交抛物线和线段BC于点P和点F,动直线l在抛物线的对称轴的右侧(不含对称轴)沿x轴正方向移动到B点.
(1)求二次函数解析式;
(2)在动直线l移动的过程中,试求使四边形DEFP为平行四边形的点P的坐标;
(3)连接CP,CD,在移动直线l移动的过程中,抛物线上是否存在点P,使得以点P,C,F为顶点的三角形与相似,如果存在,求出点P的坐标,如果不存在,请说明理由.
17.已知:如图,,与交于点,过点作,交于点.当,
时,求的长.
18.如图,在正方形中,点E在对角线上,,过点E的直线分别交,于点M,N.
(1)当时,的长为________,________;
(2)已知.
①若,求此时的长;
②当E,F为的三等分点,点P在正方形的边上时,是否存在满足的情况?如果存在,请通过分析指出这样的点的个数;如果不存在,说明理由.
19.已知:如图①,在中,,,,将绕中点旋转得到.如图②,再将沿的方向以的速度平移得到;同时,点从点出发,沿方向以的速度运动,当点停止运动时,也停止平移,设运动时间为.解答下列问题.
(1)当为何值时,?
(2)在运动过程中,为何值时的面积最大?并求面积的最大值;
(3)是否存在某一时刻,使?若存在,请求出的值;若不存在,请说明理由.
20.如果三角形的两个内角与满足=90°,那么我们称这样的三角形为“准互余三角形”.
(1)若△ABC是“准互余三角形”,∠C>90°,∠A=60°,求∠B的度数;
(2)如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5,若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.
21.如图,已知抛物线与x轴交于,两点,与y轴交于点C,其顶点为,连接与抛物线的对称轴交于点.
(1)求抛物线的表达式并写出该抛物线的对称轴;
(2)在直线上方的抛物线上找一点,使得的面积最大,求出此时点的坐标;
(3)点是对称轴右侧抛物线上的动点,在射线上是否存在点,使得以点为顶点的三角形与相似?若存在,求出点的坐标;若不存在,请说明理由.
22.如图1,正方形ABCD和正方形AEFG,连接DG,BE
(1)[发现]:当正方形AEFG绕点A旋转,如图2,线段DG与BE之间的数量关系是____;位置关系是___;
(2)[探究]:如图3,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE,猜想DG与BE的数量关系与位置关系,并说明理由;
(3)
[应用]:在(2)情况下,连结GE(点E在AB上方),若GE//AB,且AB=,AE=1,求线段DG的长
23.如图,抛物线与轴相交于点,与轴交于点,点是第二象限内抛物线上一动点,点是轴上一动点.
(1)求这条抛物线的解析式;
(2)当取最大值时,判断点是否为抛物线顶点;
(3)若点为抛物线顶点,连接,把线段绕点旋转,使得旋转后的线段与线段有交点,请求出的取值范围.
【参考答案】
1.C
2.B
3.B
4.A
5.B
6.C
7.B
8.C
9.B
10.D
11.6
12.
13.
14.
15.3
16.(1);(2);(3)存在点P,使得以点P,C,F为顶点的三角形与相似,此时.
17.OE=2.
18.(1);;(2)①;②存在,有8个.
19.(1);(2)当时,有最大值,最大值为;(3)存在,
20.(1)∠B=15°;(2)存在,BE=.
21.(1),;(2)P(2,4);(3)存在,M的坐标为:或或
22.(1)BE=DG,BE⊥DG;(2)DG=2
BE,BE⊥DG,理由见详解;(3)4
23.(1);(2)不是;(3)
第二十七章
相似
综合训练题4
一、选择题
1.在中,,,的角平分线交于点D,则的长为(
)
A.5
B.
C.
D.
2.已知点是线段的黄金分割点,,则的值为(
)
A.
B.
C.0.618
D.
3.如图,中,于点,下列条件中不能判定是直角三角形的是(
)
A.
B.
C.
D.
4.如图,,若,则的值是(
)
A.2
B.
C.
D.3
5.如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为2米,旗杆底部与平面镜的水平距离为16米,若小明的眼睛与地面距离为1.5米,则旗杆的高度为(
)
A.米
B.12米
C.9米
D.米
6.如图,点M是正方形ABCD内一点,△MBC是等边三角形,连接AM、MD.对角线BD交CM于点N,现有以下结论不正确的是(
)
A.
B.
C.
D.
7.如图,中,,点D是AB的中点,连接CD,过点B作,分别交CD,CA于点E,F,与过点A且垂直于AB的直线相交于点G,下列结论正确地是()
A.
B.
C.AB
D.
8.如图,矩形中,,,点从点出发,按的方向在和上移动,记,点到直线的距离为,则关于的函数大致图象是(
)
A.
B.
C.
D.
9.在矩形ABCD中,AB=4,BC=2,E为BC中点,H,G分别是边AB,CD上的动点,且始终保持GH⊥AE,则EH+AG最小值为(
)
A.
B.
C.
D.
10.已知如图,在正方形ABCD中AD=4,E,F分别是CD,BC上的一点,且∠EAF=45°,EC=1,将△AED绕点A沿顺时针方向旋转90°后与△ABG重合,连接EF,过点B作BM∥AG交AF于M,则下面结论:①△AGF≌△AEF;②DE+BF=EF;③BF=;④,其中正确的个数为(
)
A.1
B.2
C.3
D.4
二、填空题
11.如图,在中,,点A在反比例函数的图象上,点在x轴上,且,延长交y轴于点D,连接,若的面积等于2,则k的值为______.
12.如图,直线与坐标轴分别交于点,与直线交于点是线段上的动点,连接,若,则点的坐标为___________.
13.如图,在中,,,,点P在边上,联结,将绕着点A旋转,使得点P与边的中点M重合,点B的对应点是点,延长交于E,则的长等于_____.
14.如图,在锐角三角形ABC中,,,点D为边AB的中点,点E在边AC上,将沿DE折叠得到.若,则的值为_______;的值为________.
15.如图,在菱形中,,点在边上,且,动点从点出发,沿着运动到点停止,过点作交菱形的边于点,若线段的中点为.当点与点重合时,的长为____,点从点运动到点的过程中,点的运动路线长为____.
三、解答题
16.如图,二次函数的图象与x轴交于点,,与y轴交于点C,抛物线的顶点为D,其对称轴与线段BC交于点E.垂直于x轴的动直线l分别交抛物线和线段BC于点P和点F,动直线l在抛物线的对称轴的右侧(不含对称轴)沿x轴正方向移动到B点.
(1)求二次函数解析式;
(2)在动直线l移动的过程中,试求使四边形DEFP为平行四边形的点P的坐标;
(3)连接CP,CD,在移动直线l移动的过程中,抛物线上是否存在点P,使得以点P,C,F为顶点的三角形与相似,如果存在,求出点P的坐标,如果不存在,请说明理由.
17.已知:如图,,与交于点,过点作,交于点.当,
时,求的长.
18.如图,在正方形中,点E在对角线上,,过点E的直线分别交,于点M,N.
(1)当时,的长为________,________;
(2)已知.
①若,求此时的长;
②当E,F为的三等分点,点P在正方形的边上时,是否存在满足的情况?如果存在,请通过分析指出这样的点的个数;如果不存在,说明理由.
19.已知:如图①,在中,,,,将绕中点旋转得到.如图②,再将沿的方向以的速度平移得到;同时,点从点出发,沿方向以的速度运动,当点停止运动时,也停止平移,设运动时间为.解答下列问题.
(1)当为何值时,?
(2)在运动过程中,为何值时的面积最大?并求面积的最大值;
(3)是否存在某一时刻,使?若存在,请求出的值;若不存在,请说明理由.
20.如果三角形的两个内角与满足=90°,那么我们称这样的三角形为“准互余三角形”.
(1)若△ABC是“准互余三角形”,∠C>90°,∠A=60°,求∠B的度数;
(2)如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5,若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.
21.如图,已知抛物线与x轴交于,两点,与y轴交于点C,其顶点为,连接与抛物线的对称轴交于点.
(1)求抛物线的表达式并写出该抛物线的对称轴;
(2)在直线上方的抛物线上找一点,使得的面积最大,求出此时点的坐标;
(3)点是对称轴右侧抛物线上的动点,在射线上是否存在点,使得以点为顶点的三角形与相似?若存在,求出点的坐标;若不存在,请说明理由.
22.如图1,正方形ABCD和正方形AEFG,连接DG,BE
(1)[发现]:当正方形AEFG绕点A旋转,如图2,线段DG与BE之间的数量关系是____;位置关系是___;
(2)[探究]:如图3,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE,猜想DG与BE的数量关系与位置关系,并说明理由;
(3)
[应用]:在(2)情况下,连结GE(点E在AB上方),若GE//AB,且AB=,AE=1,求线段DG的长
23.如图,抛物线与轴相交于点,与轴交于点,点是第二象限内抛物线上一动点,点是轴上一动点.
(1)求这条抛物线的解析式;
(2)当取最大值时,判断点是否为抛物线顶点;
(3)若点为抛物线顶点,连接,把线段绕点旋转,使得旋转后的线段与线段有交点,请求出的取值范围.
【参考答案】
1.C
2.B
3.B
4.A
5.B
6.C
7.B
8.C
9.B
10.D
11.6
12.
13.
14.
15.3
16.(1);(2);(3)存在点P,使得以点P,C,F为顶点的三角形与相似,此时.
17.OE=2.
18.(1);;(2)①;②存在,有8个.
19.(1);(2)当时,有最大值,最大值为;(3)存在,
20.(1)∠B=15°;(2)存在,BE=.
21.(1),;(2)P(2,4);(3)存在,M的坐标为:或或
22.(1)BE=DG,BE⊥DG;(2)DG=2
BE,BE⊥DG,理由见详解;(3)4
23.(1);(2)不是;(3)
