2020-2021人教版数学九年级下册第27章相似常考题专练(word版含答案)
文档属性
| 名称 | 2020-2021人教版数学九年级下册第27章相似常考题专练(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-27 05:39:14 | ||
图片预览

文档简介
人教版数学九年级下册第27章《相似》
常考题专练(五)
1.如图1,在直角梯形ABCD中,AD∥BC,顶点D,C分别在AM,BN上运动(点D不与A重合,点C不与B重合),E是AB上的动点(点E不与A,B重合),在运动过程中始终保持DE⊥CE,且AD+DE=AB=a.
(1)求证:△ADE∽△BEC;
(2)当点E为AB边的中点时(如图2),求证:①AD+BC=CD;②DE,CE分别平分∠ADC,∠BCD;
(3)设AE=m,请探究:△BEC的周长是否与m值有关,若有关请用含m的代数式表示△BEC的周长;若无关请说明理由.
2.如图1,点A、B分别是两条平行线m、n上任意两点,在直线n上找一点C,使BC=kAB(k为常数),连接AC,在直线AC上任取一点E,作∠BEF=∠ABC,EF交直线m于点F.
(1)请说明∠AFE=∠ABE的理由;
(2)当k=1时,探究线段EF与EB的数量关系,并加以说明;
(3)当k≠1时,探究线段EF与EB的比值,请说明理由.
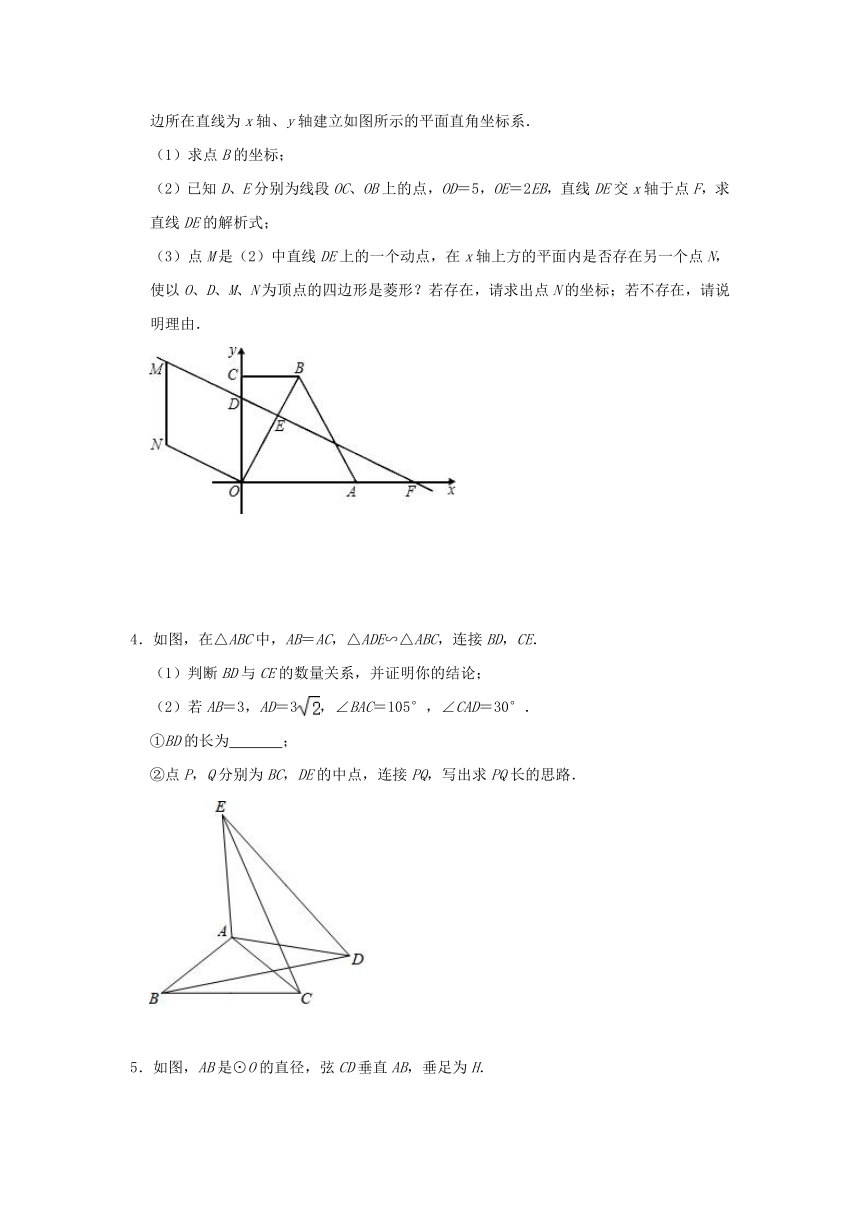
3.在直角梯形OABC中,CB∥OA,∠COA=90°,CB=3,OA=6,BA=.分别以OA、OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系.
(1)求点B的坐标;
(2)已知D、E分别为线段OC、OB上的点,OD=5,OE=2EB,直线DE交x轴于点F,求直线DE的解析式;
(3)点M是(2)中直线DE上的一个动点,在x轴上方的平面内是否存在另一个点N,使以O、D、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.
4.如图,在△ABC中,AB=AC,△ADE∽△ABC,连接BD,CE.
(1)判断BD与CE的数量关系,并证明你的结论;
(2)若AB=3,AD=3,∠BAC=105°,∠CAD=30°.
①BD的长为
;
②点P,Q分别为BC,DE的中点,连接PQ,写出求PQ长的思路.
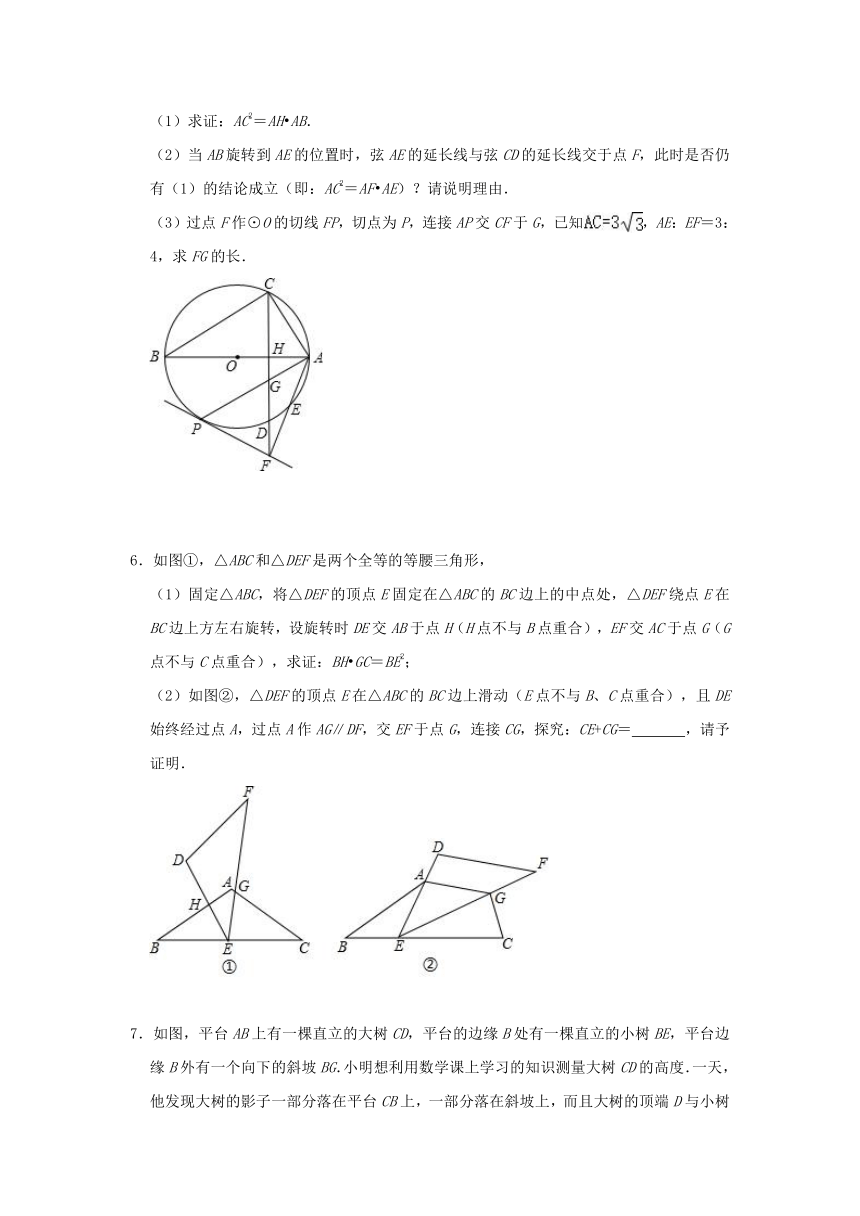
5.如图,AB是⊙O的直径,弦CD垂直AB,垂足为H.
(1)求证:AC2=AH?AB.
(2)当AB旋转到AE的位置时,弦AE的延长线与弦CD的延长线交于点F,此时是否仍有(1)的结论成立(即:AC2=AF?AE)?请说明理由.
(3)过点F作⊙O的切线FP,切点为P,连接AP交CF于G,已知,AE:EF=3:4,求FG的长.
6.如图①,△ABC和△DEF是两个全等的等腰三角形,
(1)固定△ABC,将△DEF的顶点E固定在△ABC的BC边上的中点处,△DEF绕点E在BC边上方左右旋转,设旋转时DE交AB于点H(H点不与B点重合),EF交AC于点G(G点不与C点重合),求证:BH?GC=BE2;
(2)如图②,△DEF的顶点E在△ABC的BC边上滑动(E点不与B、C点重合),且DE始终经过点A,过点A作AG∥DF,交EF于点G,连接CG,探究:CE+CG=
,请予证明.
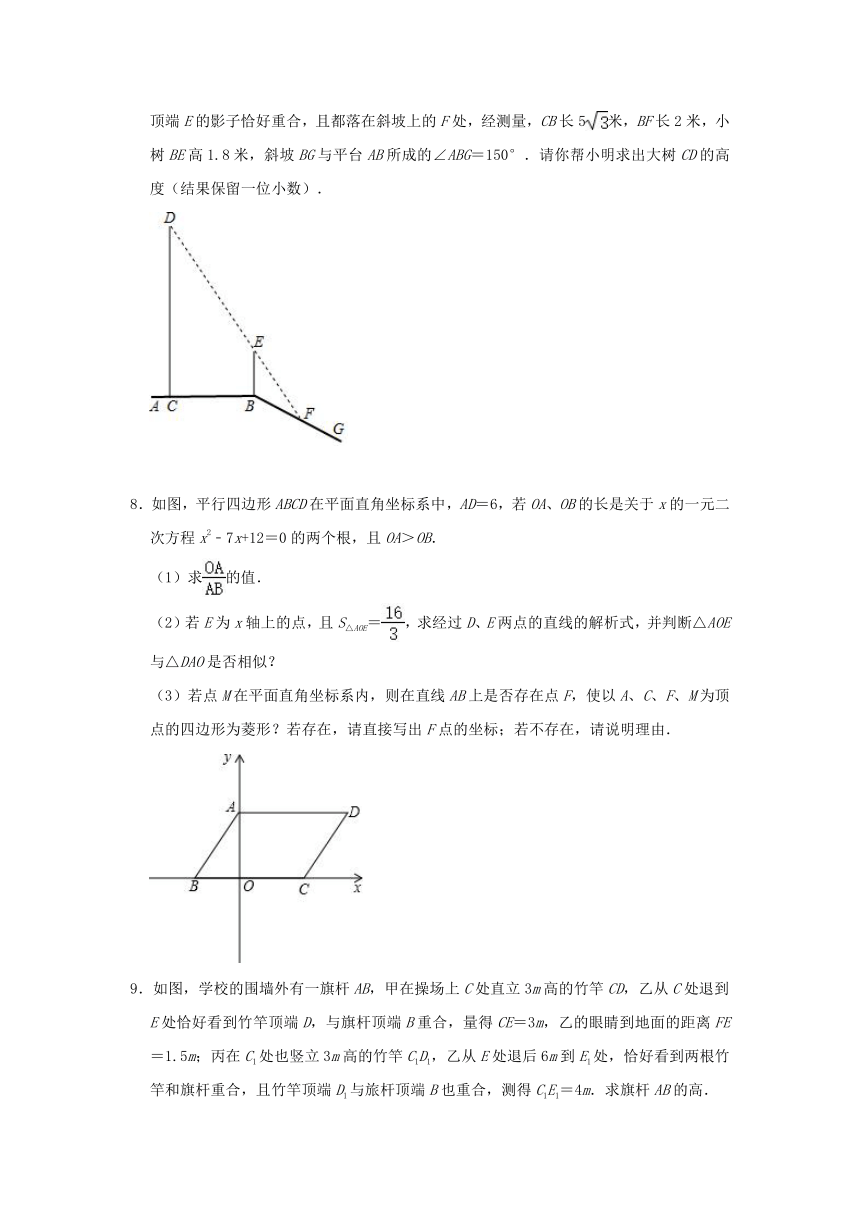
7.如图,平台AB上有一棵直立的大树CD,平台的边缘B处有一棵直立的小树BE,平台边缘B外有一个向下的斜坡BG.小明想利用数学课上学习的知识测量大树CD的高度.一天,他发现大树的影子一部分落在平台CB上,一部分落在斜坡上,而且大树的顶端D与小树顶端E的影子恰好重合,且都落在斜坡上的F处,经测量,CB长5米,BF长2米,小树BE高1.8米,斜坡BG与平台AB所成的∠ABG=150°.请你帮小明求出大树CD的高度(结果保留一位小数).
8.如图,平行四边形ABCD在平面直角坐标系中,AD=6,若OA、OB的长是关于x的一元二次方程x2﹣7x+12=0的两个根,且OA>OB.
(1)求的值.
(2)若E为x轴上的点,且S△AOE=,求经过D、E两点的直线的解析式,并判断△AOE与△DAO是否相似?
(3)若点M在平面直角坐标系内,则在直线AB上是否存在点F,使以A、C、F、M为顶点的四边形为菱形?若存在,请直接写出F点的坐标;若不存在,请说明理由.
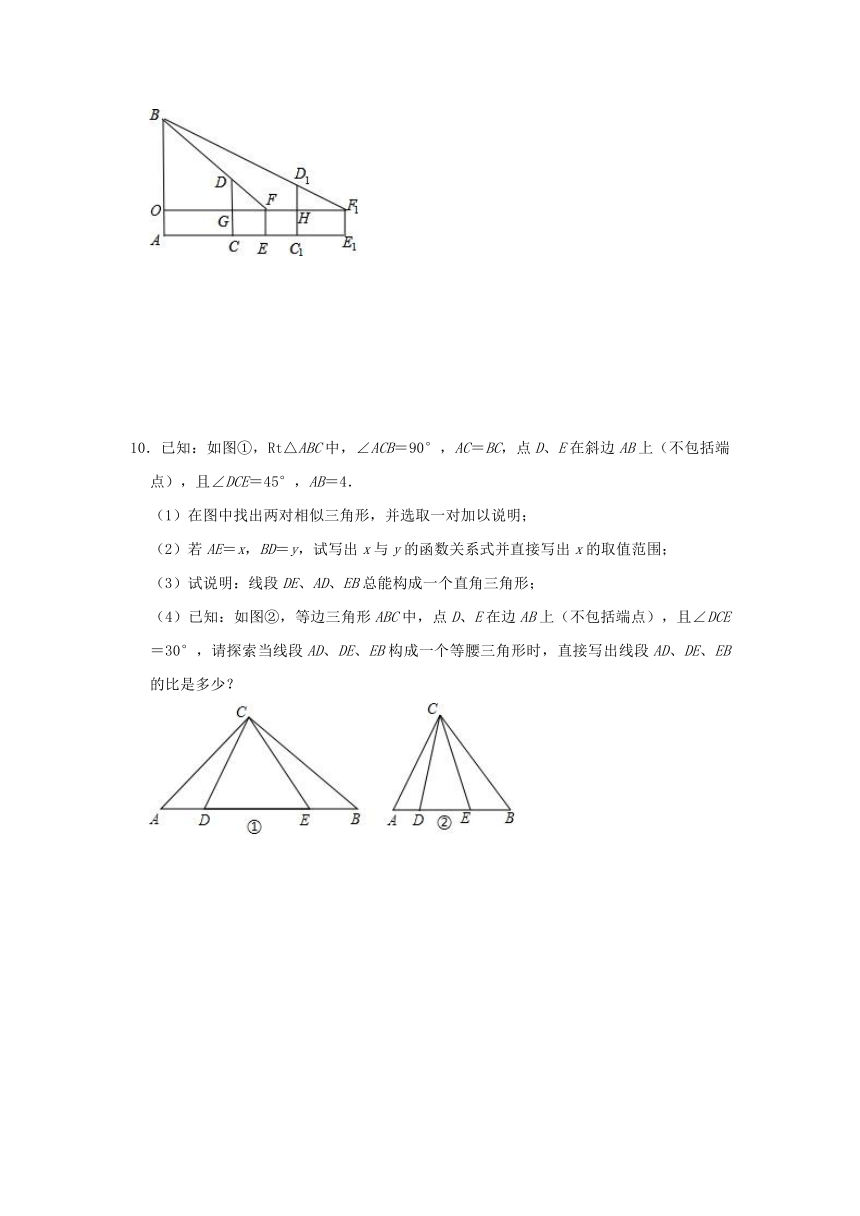
9.如图,学校的围墙外有一旗杆AB,甲在操场上C处直立3m高的竹竿CD,乙从C处退到E处恰好看到竹竿顶端D,与旗杆顶端B重合,量得CE=3m,乙的眼睛到地面的距离FE=1.5m;丙在C1处也竖立3m高的竹竿C1D1,乙从E处退后6m到E1处,恰好看到两根竹竿和旗杆重合,且竹竿顶端D1与旅杆顶端B也重合,测得C1E1=4m.求旗杆AB的高.
10.已知:如图①,Rt△ABC中,∠ACB=90°,AC=BC,点D、E在斜边AB上(不包括端点),且∠DCE=45°,AB=4.
(1)在图中找出两对相似三角形,并选取一对加以说明;
(2)若AE=x,BD=y,试写出x与y的函数关系式并直接写出x的取值范围;
(3)试说明:线段DE、AD、EB总能构成一个直角三角形;
(4)已知:如图②,等边三角形ABC中,点D、E在边AB上(不包括端点),且∠DCE=30°,请探索当线段AD、DE、EB构成一个等腰三角形时,直接写出线段AD、DE、EB的比是多少?
参考答案
1.(1)证明:∵梯形ABCD是直角梯形
∴∠A=∠B=90°
又∵∠DEC=90°
∴∠AED+∠BEC=90°
∵∠BEC+∠BCE=90°
∴∠AED=∠BCE
∴△ADE∽△BEC
(2)证明:过点E作EF∥AD,交CD于F,则EF既是梯形ABCD的中位线,又是Rt△DEC斜边上的中线.
∵AD+BC=2EF,CD=2EF
∴AD+BC=CD
∵FD=FE=CD
∴∠FDE=∠FED
∵EF∥AD
∴∠ADE=∠FED
∴∠FDE=∠ADE,即DE平分∠ADC
同理可证:CE平分∠BCD
(3)解:设AD=x,由已知AD+DE=AB=a得DE=a﹣x,又AE=m
在Rt△AED中,由勾股定理得:x2+m2=(a﹣x)2,化简整理得:a2﹣m2=2ax①
在△EBC中,由AE=m,AB=a,得BE=a﹣m
因为△ADE∽△BEC,所以,
即:,
解得:
所以△BEC的周长=BE+BC+EC=
==
=②
把①式代入②,得△BEC的周长=BE+BC+EC=
所以△BEC的周长与m无关.
2.解:(1)∵m∥n,
∴∠FAB=∠ABC,
∵∠FEB=∠ABC,
∴∠FAB=∠FEB,
∵∠AOF=∠EOB,
∴△AOF∽△EOB,
∴∠AFE=∠ABE;
(2)作ED⊥m,EP⊥AB,
∵k=1,
∴AB=BC,
∴∠BAC=∠ACB,
∵m∥n,
∴∠DAE=∠ACB,
∴∠DAE=∠BAC,
∴ED=EP(角平分线上的点到角的两边的距离相等),
在△FDE和△EPB中,,
∴△FDE≌△EPB(AAS),
∴EF=EB(全等三角形对应边相等);
(3)连接FB,设AB与EF交于点O,
在△AOF和△EOB中,,
∴△AOF∽△EOB,
∴,
又∵∠AOE=∠FOB,
∴△AOE∽△FOB,
∴∠CAB=∠EFB,
∵∠FEB=∠ABC,
∴△ACB∽△FBE,
∴.
3.解:(1)作BH⊥x轴于点H,则四边形OHBC为矩形,
∴OH=CB=3,
∴AH=OA﹣OH=6﹣3=3,
在Rt△ABH中,BH===6,
∴点B的坐标为(3,6);
(2)作EG⊥x轴于点G,则EG∥BH,
∴△OEG∽△OBH,
∴,
又∵OE=2EB,
∴,
∴=,
∴OG=2,EG=4,
∴点E的坐标为(2,4),
又∵点D的坐标为(0,5),
设直线DE的解析式为y=kx+b,
则,
解得k=﹣,b=5,
∴直线DE的解析式为:y=﹣x+5;
(3)答:存在;
①如图1,当OD=DM=MN=NO=5时,四边形ODMN为菱形.作MP⊥y轴于点P,则MP∥x轴,∴△MPD∽△FOD
∴,
又∵当y=0时,﹣x+5=0,
解得x=10,
∴F点的坐标为(10,0),
∴OF=10,
在Rt△ODF中,FD===5,
∴,
∴MP=2,PD=,
∴点M的坐标为(﹣2,5+),
∴点N的坐标为(﹣2,);
②如图2,当OD=DN=NM=MO=5时,四边形ODNM为菱形.延长NM交x轴于点P,则MP⊥x轴.
∵点M在直线y=﹣x+5上,
∴设M点坐标为(a,﹣a+5),
在Rt△OPM中,OP2+PM2=OM2,
∴a2+(﹣a+5)2=52,
解得:a1=4,a2=0(舍去),
∴点M的坐标为(4,3),
∴点N的坐标为(4,8);
③如图3,当OM=MD=DN=NO时,四边形OMDN为菱形,连接NM,交OD于点P,则NM与OD互相垂直平分,
∴yM=yN=OP=,
∴﹣xM+5=,
∴xM=5,
∴xN=﹣xM=﹣5,
∴点N的坐标为(﹣5,),
综上所述,x轴上方的点N有三个,分别为N1(﹣2,),N2(4,8),N3(﹣5,).
(其它解法可参照给分)
4.解:(1)结论:BD=CE,
理由:∵△ADE∽△ABC,
∴∠BAC=∠DAE,
∴∠BAC+∠CAD=∠CAD+∠DAE,
即∠BAD=∠CAE,
在△ABD与△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE;
(2)①如图1中,作DH⊥BA交BA的延长线于H.
∵∠BAD=∠BAC+∠DAC=135°,
∴∠DAH=45°,
∵∠H=90°,AD=3,
∴AH=DH=3,
在Rt△BDH中,BD===3,
故答案为:3;
(2)如图2中,连接PQ,AQ,AP,作QH⊥PA交PA的延长线于H.
在Rt△ABP中,AP=AB?sin37.5°,
在Rt△AQD中,AQ=AD?sin37.5°,
在Rt△AHQ中,根据∠HAQ=45°,可得AH=HQ=AQ,
求出HQ,PH,根据PQ=计算即可.
5.解:(1)证明:∵AB是直径,且CD⊥AB,∠ACB=∠AHC,
∴△ABC∽△ACH,
∴,即AC2=AH?AB.
(2)上面的结论成立.
连接CE;
∵直径AB⊥CD,
∴,即∠CEA=∠ACF,
又∵∠CAE=∠FAC,
∴△ACF∽△AEC,
∴AC2=AE?AF.
(3)连接OP,则OP⊥PF;
∵∠GPF=90°﹣∠OPA,∠AGH=90°﹣∠OAP,
且∠OPA=∠OAP,∠AGH=∠PGF,
∴∠GPF=∠PGF,即FP=FG;
设AE=3x,EF=4x;
∵AC2=AF?AE,
∴,∴;
由切割线定理得:FP2=EF?AF,∴FP2=4x?7x=28x2=36,
∴FP=6,
故FG=FP=6.
6.解:(1)∵△ABC和△DEF是全等的等腰三角形
∴∠B=∠C=∠DEF=∠F,
∵∠DEC=∠B+∠BHE=∠DEF+∠GEC
∴∠BHE=∠GEC,
∴△BEH∽△CGE,
∴
即BE?CE=CG?BH,
∵点E是BC的中点
∴BE=CE,
∴BH?GC=BE2
(2)解:∵AG∥DF,
∴∠AGE=∠F,∠EAG=∠D
∵∠F=∠DEF,
∴∠AGE=∠DEF,
∴AE=AG,
∵∠BAC=∠D,
∴∠BAC=∠EAG,
∴∠BAE=∠CAG,
在△ABE和△ACG中,,
∴△ABE≌△ACG(SAS),
∴BE=CG,
∴CE+CG=CE+BE=BC;
故答案为:BC.
7.解:延长CB交EF于点H,过点F作FM⊥EB的延长线于点M
∵∠ABG=150°,BE⊥CB
∴∠MBF=150°﹣90°=60°
∴∠MFB=30°
∵BF的长为2米,
∴BM=1米,MF=米
∵BE⊥CB,MF⊥BE
∴BH∥MF
∴△EBH∽△EMF
∴=
又∵EB=1.8米
∴=
∴BH=
∵BE∥CD
∴△HBE∽△HCD
∴=
∵CB=5
∴=
∴CD=15.8米
∴大树CD的高度为15.8米.
8.解:(1)x2﹣7x+12=0,
(x﹣3)(x﹣4)=0,
∴x﹣3=0,x﹣4=0,
解得x1=3,x2=4,
∵OA>OB,
∴OA=4,OB=3,
在△AOB中,AB===5,
∴sin∠ABC==;
(2)根据题意,设E(x,0),则
S△AOE=×OA×x=×4x=,
解得x=,
∴E(,0)或(﹣,0),
∵四边形ABCD是平行四边形,
∴点D的坐标是(6,4),
设经过D、E两点的直线的解析式为y=kx+b,
则①,
解得
,
∴解析式为y=x﹣;
②,
解得,
解析式为:y=x+,
在△AOE与△DAO中,==,
==,
∴=,
又∵∠AOE=∠OAD=90°,
∴△AOE∽△DAO;
(3)根据计算的数据,OB=OC=3,
∴AO平分∠BAC,
①AC、AF是邻边,点F在射线AB上时,AF=AC=5,
所以点F与B重合,
即F(﹣3,0),
②AC、AF是邻边,点F在射线BA上时,M应在直线AD上,且FC垂直平分AM,
点F(3,8).
③AC是对角线时,做AC垂直平分线L,AC解析式为y=﹣x+4,直线L过(,2),且k值为(平面内互相垂直的两条直线k值乘积为﹣1),
L解析式为y=x+,联立直线L与直线AB求交点,
∴F(﹣,﹣),
④AF是对角线时,过C做AB垂线,垂足为N,根据等积法求出CN=,勾股定理得出,AN=,做A关于N的对称点即为F,AF=,过F做y轴垂线,垂足为G,FG=×=,
∴F(﹣,).
综上所述,满足条件的点有四个:F1(﹣3,0);F2(3,8);F3(﹣,﹣);F4(﹣,).
9.解:设BO=x,GO=y.
∵GD∥OB,
∴△DGF∽△BOF,
∴1.5:x=3:(3+y)
同理1.5:x=4:(y+6+3)
解上面2个方程得
,
经检验x=9,y=15均是原方程的解,
∴旗杆AB的高为9+1.5=10.5(米).
10.解:(1)△AEC∽△CED,△AEC∽△BCD.
∵∠ACD+∠DCE=∠ACD+45°,
∴∠ACE=∠BDC,
∴△AEC∽△BCD;
(2)∵∠A=∠B=45°,∠AEC=∠DCB=45°+∠BCE,
∴△AEC∽△BCD,
∴BD?AE=AC2,
∴BD?AE=AC2=×AB2=8,
(2<x<4).
(3)证明如下:将△ABC绕点C顺时针旋转90°,
设E点对应点为E′,连接E′D,
∵∠ACB=90°,AC=BC,
∴旋转后B与A重合,
又∵∠DCE=45°,
∴∠E′CD′=45°,
又∵CE′=CE,CD为公共边,
∴△CE′D≌△CED,
∴DE′=DE,
又∵∠E′AC=45°,∠CAD=45°,
∴∠E′AD=90°,
∴线段DE、AD、EA总能构成一个直角三角形;
(4)AD:DE:EB=1::1.
常考题专练(五)
1.如图1,在直角梯形ABCD中,AD∥BC,顶点D,C分别在AM,BN上运动(点D不与A重合,点C不与B重合),E是AB上的动点(点E不与A,B重合),在运动过程中始终保持DE⊥CE,且AD+DE=AB=a.
(1)求证:△ADE∽△BEC;
(2)当点E为AB边的中点时(如图2),求证:①AD+BC=CD;②DE,CE分别平分∠ADC,∠BCD;
(3)设AE=m,请探究:△BEC的周长是否与m值有关,若有关请用含m的代数式表示△BEC的周长;若无关请说明理由.
2.如图1,点A、B分别是两条平行线m、n上任意两点,在直线n上找一点C,使BC=kAB(k为常数),连接AC,在直线AC上任取一点E,作∠BEF=∠ABC,EF交直线m于点F.
(1)请说明∠AFE=∠ABE的理由;
(2)当k=1时,探究线段EF与EB的数量关系,并加以说明;
(3)当k≠1时,探究线段EF与EB的比值,请说明理由.
3.在直角梯形OABC中,CB∥OA,∠COA=90°,CB=3,OA=6,BA=.分别以OA、OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系.
(1)求点B的坐标;
(2)已知D、E分别为线段OC、OB上的点,OD=5,OE=2EB,直线DE交x轴于点F,求直线DE的解析式;
(3)点M是(2)中直线DE上的一个动点,在x轴上方的平面内是否存在另一个点N,使以O、D、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.
4.如图,在△ABC中,AB=AC,△ADE∽△ABC,连接BD,CE.
(1)判断BD与CE的数量关系,并证明你的结论;
(2)若AB=3,AD=3,∠BAC=105°,∠CAD=30°.
①BD的长为
;
②点P,Q分别为BC,DE的中点,连接PQ,写出求PQ长的思路.
5.如图,AB是⊙O的直径,弦CD垂直AB,垂足为H.
(1)求证:AC2=AH?AB.
(2)当AB旋转到AE的位置时,弦AE的延长线与弦CD的延长线交于点F,此时是否仍有(1)的结论成立(即:AC2=AF?AE)?请说明理由.
(3)过点F作⊙O的切线FP,切点为P,连接AP交CF于G,已知,AE:EF=3:4,求FG的长.
6.如图①,△ABC和△DEF是两个全等的等腰三角形,
(1)固定△ABC,将△DEF的顶点E固定在△ABC的BC边上的中点处,△DEF绕点E在BC边上方左右旋转,设旋转时DE交AB于点H(H点不与B点重合),EF交AC于点G(G点不与C点重合),求证:BH?GC=BE2;
(2)如图②,△DEF的顶点E在△ABC的BC边上滑动(E点不与B、C点重合),且DE始终经过点A,过点A作AG∥DF,交EF于点G,连接CG,探究:CE+CG=
,请予证明.
7.如图,平台AB上有一棵直立的大树CD,平台的边缘B处有一棵直立的小树BE,平台边缘B外有一个向下的斜坡BG.小明想利用数学课上学习的知识测量大树CD的高度.一天,他发现大树的影子一部分落在平台CB上,一部分落在斜坡上,而且大树的顶端D与小树顶端E的影子恰好重合,且都落在斜坡上的F处,经测量,CB长5米,BF长2米,小树BE高1.8米,斜坡BG与平台AB所成的∠ABG=150°.请你帮小明求出大树CD的高度(结果保留一位小数).
8.如图,平行四边形ABCD在平面直角坐标系中,AD=6,若OA、OB的长是关于x的一元二次方程x2﹣7x+12=0的两个根,且OA>OB.
(1)求的值.
(2)若E为x轴上的点,且S△AOE=,求经过D、E两点的直线的解析式,并判断△AOE与△DAO是否相似?
(3)若点M在平面直角坐标系内,则在直线AB上是否存在点F,使以A、C、F、M为顶点的四边形为菱形?若存在,请直接写出F点的坐标;若不存在,请说明理由.
9.如图,学校的围墙外有一旗杆AB,甲在操场上C处直立3m高的竹竿CD,乙从C处退到E处恰好看到竹竿顶端D,与旗杆顶端B重合,量得CE=3m,乙的眼睛到地面的距离FE=1.5m;丙在C1处也竖立3m高的竹竿C1D1,乙从E处退后6m到E1处,恰好看到两根竹竿和旗杆重合,且竹竿顶端D1与旅杆顶端B也重合,测得C1E1=4m.求旗杆AB的高.
10.已知:如图①,Rt△ABC中,∠ACB=90°,AC=BC,点D、E在斜边AB上(不包括端点),且∠DCE=45°,AB=4.
(1)在图中找出两对相似三角形,并选取一对加以说明;
(2)若AE=x,BD=y,试写出x与y的函数关系式并直接写出x的取值范围;
(3)试说明:线段DE、AD、EB总能构成一个直角三角形;
(4)已知:如图②,等边三角形ABC中,点D、E在边AB上(不包括端点),且∠DCE=30°,请探索当线段AD、DE、EB构成一个等腰三角形时,直接写出线段AD、DE、EB的比是多少?
参考答案
1.(1)证明:∵梯形ABCD是直角梯形
∴∠A=∠B=90°
又∵∠DEC=90°
∴∠AED+∠BEC=90°
∵∠BEC+∠BCE=90°
∴∠AED=∠BCE
∴△ADE∽△BEC
(2)证明:过点E作EF∥AD,交CD于F,则EF既是梯形ABCD的中位线,又是Rt△DEC斜边上的中线.
∵AD+BC=2EF,CD=2EF
∴AD+BC=CD
∵FD=FE=CD
∴∠FDE=∠FED
∵EF∥AD
∴∠ADE=∠FED
∴∠FDE=∠ADE,即DE平分∠ADC
同理可证:CE平分∠BCD
(3)解:设AD=x,由已知AD+DE=AB=a得DE=a﹣x,又AE=m
在Rt△AED中,由勾股定理得:x2+m2=(a﹣x)2,化简整理得:a2﹣m2=2ax①
在△EBC中,由AE=m,AB=a,得BE=a﹣m
因为△ADE∽△BEC,所以,
即:,
解得:
所以△BEC的周长=BE+BC+EC=
==
=②
把①式代入②,得△BEC的周长=BE+BC+EC=
所以△BEC的周长与m无关.
2.解:(1)∵m∥n,
∴∠FAB=∠ABC,
∵∠FEB=∠ABC,
∴∠FAB=∠FEB,
∵∠AOF=∠EOB,
∴△AOF∽△EOB,
∴∠AFE=∠ABE;
(2)作ED⊥m,EP⊥AB,
∵k=1,
∴AB=BC,
∴∠BAC=∠ACB,
∵m∥n,
∴∠DAE=∠ACB,
∴∠DAE=∠BAC,
∴ED=EP(角平分线上的点到角的两边的距离相等),
在△FDE和△EPB中,,
∴△FDE≌△EPB(AAS),
∴EF=EB(全等三角形对应边相等);
(3)连接FB,设AB与EF交于点O,
在△AOF和△EOB中,,
∴△AOF∽△EOB,
∴,
又∵∠AOE=∠FOB,
∴△AOE∽△FOB,
∴∠CAB=∠EFB,
∵∠FEB=∠ABC,
∴△ACB∽△FBE,
∴.
3.解:(1)作BH⊥x轴于点H,则四边形OHBC为矩形,
∴OH=CB=3,
∴AH=OA﹣OH=6﹣3=3,
在Rt△ABH中,BH===6,
∴点B的坐标为(3,6);
(2)作EG⊥x轴于点G,则EG∥BH,
∴△OEG∽△OBH,
∴,
又∵OE=2EB,
∴,
∴=,
∴OG=2,EG=4,
∴点E的坐标为(2,4),
又∵点D的坐标为(0,5),
设直线DE的解析式为y=kx+b,
则,
解得k=﹣,b=5,
∴直线DE的解析式为:y=﹣x+5;
(3)答:存在;
①如图1,当OD=DM=MN=NO=5时,四边形ODMN为菱形.作MP⊥y轴于点P,则MP∥x轴,∴△MPD∽△FOD
∴,
又∵当y=0时,﹣x+5=0,
解得x=10,
∴F点的坐标为(10,0),
∴OF=10,
在Rt△ODF中,FD===5,
∴,
∴MP=2,PD=,
∴点M的坐标为(﹣2,5+),
∴点N的坐标为(﹣2,);
②如图2,当OD=DN=NM=MO=5时,四边形ODNM为菱形.延长NM交x轴于点P,则MP⊥x轴.
∵点M在直线y=﹣x+5上,
∴设M点坐标为(a,﹣a+5),
在Rt△OPM中,OP2+PM2=OM2,
∴a2+(﹣a+5)2=52,
解得:a1=4,a2=0(舍去),
∴点M的坐标为(4,3),
∴点N的坐标为(4,8);
③如图3,当OM=MD=DN=NO时,四边形OMDN为菱形,连接NM,交OD于点P,则NM与OD互相垂直平分,
∴yM=yN=OP=,
∴﹣xM+5=,
∴xM=5,
∴xN=﹣xM=﹣5,
∴点N的坐标为(﹣5,),
综上所述,x轴上方的点N有三个,分别为N1(﹣2,),N2(4,8),N3(﹣5,).
(其它解法可参照给分)
4.解:(1)结论:BD=CE,
理由:∵△ADE∽△ABC,
∴∠BAC=∠DAE,
∴∠BAC+∠CAD=∠CAD+∠DAE,
即∠BAD=∠CAE,
在△ABD与△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE;
(2)①如图1中,作DH⊥BA交BA的延长线于H.
∵∠BAD=∠BAC+∠DAC=135°,
∴∠DAH=45°,
∵∠H=90°,AD=3,
∴AH=DH=3,
在Rt△BDH中,BD===3,
故答案为:3;
(2)如图2中,连接PQ,AQ,AP,作QH⊥PA交PA的延长线于H.
在Rt△ABP中,AP=AB?sin37.5°,
在Rt△AQD中,AQ=AD?sin37.5°,
在Rt△AHQ中,根据∠HAQ=45°,可得AH=HQ=AQ,
求出HQ,PH,根据PQ=计算即可.
5.解:(1)证明:∵AB是直径,且CD⊥AB,∠ACB=∠AHC,
∴△ABC∽△ACH,
∴,即AC2=AH?AB.
(2)上面的结论成立.
连接CE;
∵直径AB⊥CD,
∴,即∠CEA=∠ACF,
又∵∠CAE=∠FAC,
∴△ACF∽△AEC,
∴AC2=AE?AF.
(3)连接OP,则OP⊥PF;
∵∠GPF=90°﹣∠OPA,∠AGH=90°﹣∠OAP,
且∠OPA=∠OAP,∠AGH=∠PGF,
∴∠GPF=∠PGF,即FP=FG;
设AE=3x,EF=4x;
∵AC2=AF?AE,
∴,∴;
由切割线定理得:FP2=EF?AF,∴FP2=4x?7x=28x2=36,
∴FP=6,
故FG=FP=6.
6.解:(1)∵△ABC和△DEF是全等的等腰三角形
∴∠B=∠C=∠DEF=∠F,
∵∠DEC=∠B+∠BHE=∠DEF+∠GEC
∴∠BHE=∠GEC,
∴△BEH∽△CGE,
∴
即BE?CE=CG?BH,
∵点E是BC的中点
∴BE=CE,
∴BH?GC=BE2
(2)解:∵AG∥DF,
∴∠AGE=∠F,∠EAG=∠D
∵∠F=∠DEF,
∴∠AGE=∠DEF,
∴AE=AG,
∵∠BAC=∠D,
∴∠BAC=∠EAG,
∴∠BAE=∠CAG,
在△ABE和△ACG中,,
∴△ABE≌△ACG(SAS),
∴BE=CG,
∴CE+CG=CE+BE=BC;
故答案为:BC.
7.解:延长CB交EF于点H,过点F作FM⊥EB的延长线于点M
∵∠ABG=150°,BE⊥CB
∴∠MBF=150°﹣90°=60°
∴∠MFB=30°
∵BF的长为2米,
∴BM=1米,MF=米
∵BE⊥CB,MF⊥BE
∴BH∥MF
∴△EBH∽△EMF
∴=
又∵EB=1.8米
∴=
∴BH=
∵BE∥CD
∴△HBE∽△HCD
∴=
∵CB=5
∴=
∴CD=15.8米
∴大树CD的高度为15.8米.
8.解:(1)x2﹣7x+12=0,
(x﹣3)(x﹣4)=0,
∴x﹣3=0,x﹣4=0,
解得x1=3,x2=4,
∵OA>OB,
∴OA=4,OB=3,
在△AOB中,AB===5,
∴sin∠ABC==;
(2)根据题意,设E(x,0),则
S△AOE=×OA×x=×4x=,
解得x=,
∴E(,0)或(﹣,0),
∵四边形ABCD是平行四边形,
∴点D的坐标是(6,4),
设经过D、E两点的直线的解析式为y=kx+b,
则①,
解得
,
∴解析式为y=x﹣;
②,
解得,
解析式为:y=x+,
在△AOE与△DAO中,==,
==,
∴=,
又∵∠AOE=∠OAD=90°,
∴△AOE∽△DAO;
(3)根据计算的数据,OB=OC=3,
∴AO平分∠BAC,
①AC、AF是邻边,点F在射线AB上时,AF=AC=5,
所以点F与B重合,
即F(﹣3,0),
②AC、AF是邻边,点F在射线BA上时,M应在直线AD上,且FC垂直平分AM,
点F(3,8).
③AC是对角线时,做AC垂直平分线L,AC解析式为y=﹣x+4,直线L过(,2),且k值为(平面内互相垂直的两条直线k值乘积为﹣1),
L解析式为y=x+,联立直线L与直线AB求交点,
∴F(﹣,﹣),
④AF是对角线时,过C做AB垂线,垂足为N,根据等积法求出CN=,勾股定理得出,AN=,做A关于N的对称点即为F,AF=,过F做y轴垂线,垂足为G,FG=×=,
∴F(﹣,).
综上所述,满足条件的点有四个:F1(﹣3,0);F2(3,8);F3(﹣,﹣);F4(﹣,).
9.解:设BO=x,GO=y.
∵GD∥OB,
∴△DGF∽△BOF,
∴1.5:x=3:(3+y)
同理1.5:x=4:(y+6+3)
解上面2个方程得
,
经检验x=9,y=15均是原方程的解,
∴旗杆AB的高为9+1.5=10.5(米).
10.解:(1)△AEC∽△CED,△AEC∽△BCD.
∵∠ACD+∠DCE=∠ACD+45°,
∴∠ACE=∠BDC,
∴△AEC∽△BCD;
(2)∵∠A=∠B=45°,∠AEC=∠DCB=45°+∠BCE,
∴△AEC∽△BCD,
∴BD?AE=AC2,
∴BD?AE=AC2=×AB2=8,
(2<x<4).
(3)证明如下:将△ABC绕点C顺时针旋转90°,
设E点对应点为E′,连接E′D,
∵∠ACB=90°,AC=BC,
∴旋转后B与A重合,
又∵∠DCE=45°,
∴∠E′CD′=45°,
又∵CE′=CE,CD为公共边,
∴△CE′D≌△CED,
∴DE′=DE,
又∵∠E′AC=45°,∠CAD=45°,
∴∠E′AD=90°,
∴线段DE、AD、EA总能构成一个直角三角形;
(4)AD:DE:EB=1::1.
