2020-2021学年九年级数学人教版下册第27章《相似》单元培优测试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年九年级数学人教版下册第27章《相似》单元培优测试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 338.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-26 09:07:20 | ||
图片预览



文档简介
2020-2021学年九年级下册数学第27章《相似》
单元培优测试卷
一.选择题(每题3分,共30分)
1.如图,DE∥AB,如果CE:AE=1:2,DE=3,那么AB等于( )
A.6 B.9 C.12 D.13
2.分别画出下列四组图形,必是相似三角形的为( )
A.两个直角三角形
B.有一个角为110°的两个等腰三角形
C.有一个角为55°的两个等腰三角形
D.两条边对应成比例,其中一边的对角对应相等的两个三角形
3.已知线段a=2,b=4,如果线段b是线段a和c的比例中项,那么线段c的长度是( )
A.8 B.6 C. D.2
4.如图,点D、E分别在△ABC的边AB、AC上,下列各比例式不一定能推得DE∥BC的是( )
A.= B.= C.= D.=
5.如图,AB∥CD∥EF,AC=2,AE=5,BD=1.5,那么下列结论正确的是( )
A.DF= B.EF= C.CD= D.BF=
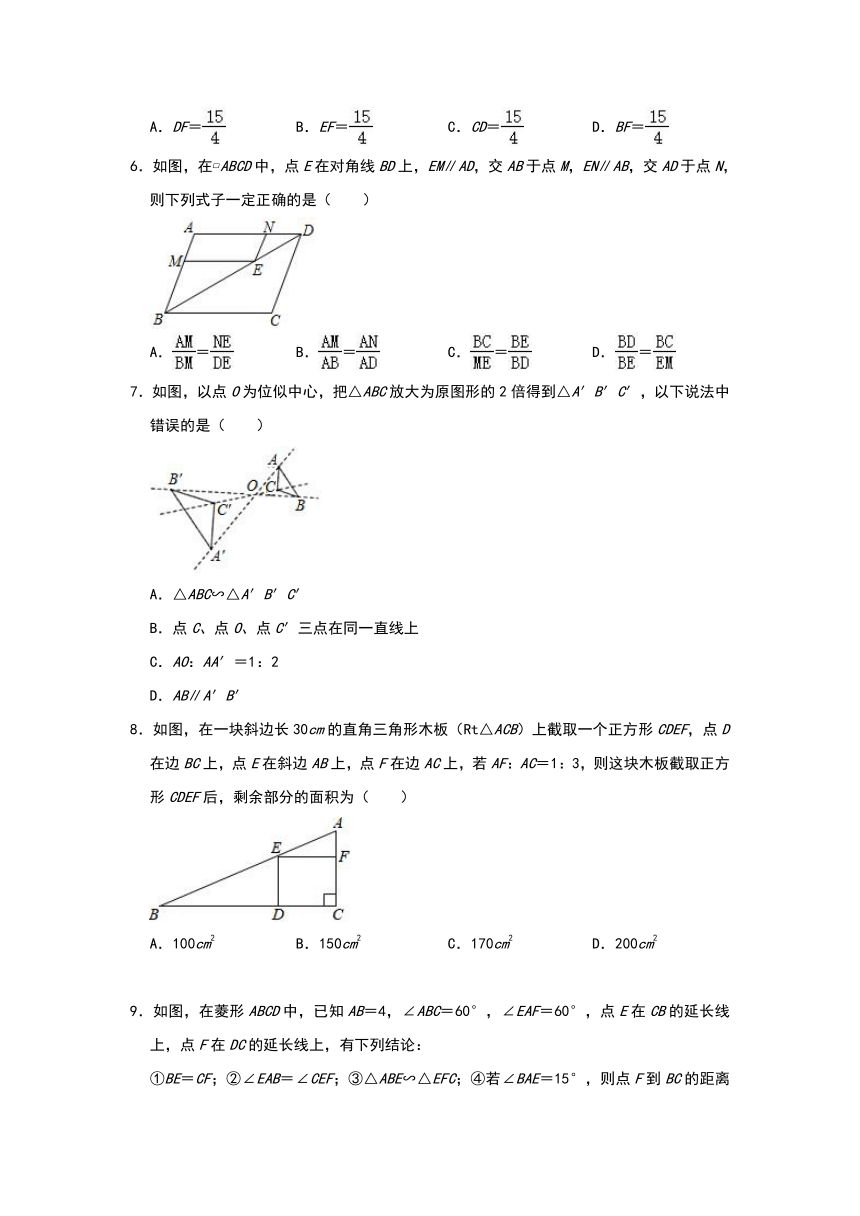
6.如图,在?ABCD中,点E在对角线BD上,EM∥AD,交AB于点M,EN∥AB,交AD于点N,则下列式子一定正确的是( )
A.= B.= C.= D.=
7.如图,以点O为位似中心,把△ABC放大为原图形的2倍得到△A′B′C′,以下说法中错误的是( )
A.△ABC∽△A′B′C′
B.点C、点O、点C′三点在同一直线上
C.AO:AA′=1:2
D.AB∥A′B′
8.如图,在一块斜边长30cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上,若AF:AC=1:3,则这块木板截取正方形CDEF后,剩余部分的面积为( )
A.100cm2 B.150cm2 C.170cm2 D.200cm2
9.如图,在菱形ABCD中,已知AB=4,∠ABC=60°,∠EAF=60°,点E在CB的延长线上,点F在DC的延长线上,有下列结论:
①BE=CF;②∠EAB=∠CEF;③△ABE∽△EFC;④若∠BAE=15°,则点F到BC的距离为2﹣2.
则其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
10.如图,正方形ABCD的边长为4,延长CB至E使EB=2,以EB为边在上方作正方形EFGB,延长FG交DC于M,连接AM,AF,H为AD的中点,连接FH分别与AB,AM交于点N、K:则下列结论:
①△ANH≌△GNF;
②∠AFN=∠HFG;
③FN=2NK;
④S△AFN:S△ADM=1:4.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(每题4分,共20分)
11.已知点P在线段AB上,且满足BP2=AB?AP,则的值等于 .
12.如图,AC与BE交于点D,∠A=∠E=90°,若点D是线段AC的中点,且AB=AC=10.则BE的长等于 .
13.如果直线l把△ABC分割后的两个部分面积相等,且周长也相等,那么就把直线l叫做△ABC的“完美分割线”,已知在△ABC中,AB=AC,△ABC的一条“完美分割线”为直线l,且直线l平行于BC,若AB=2,则BC的长等于 .
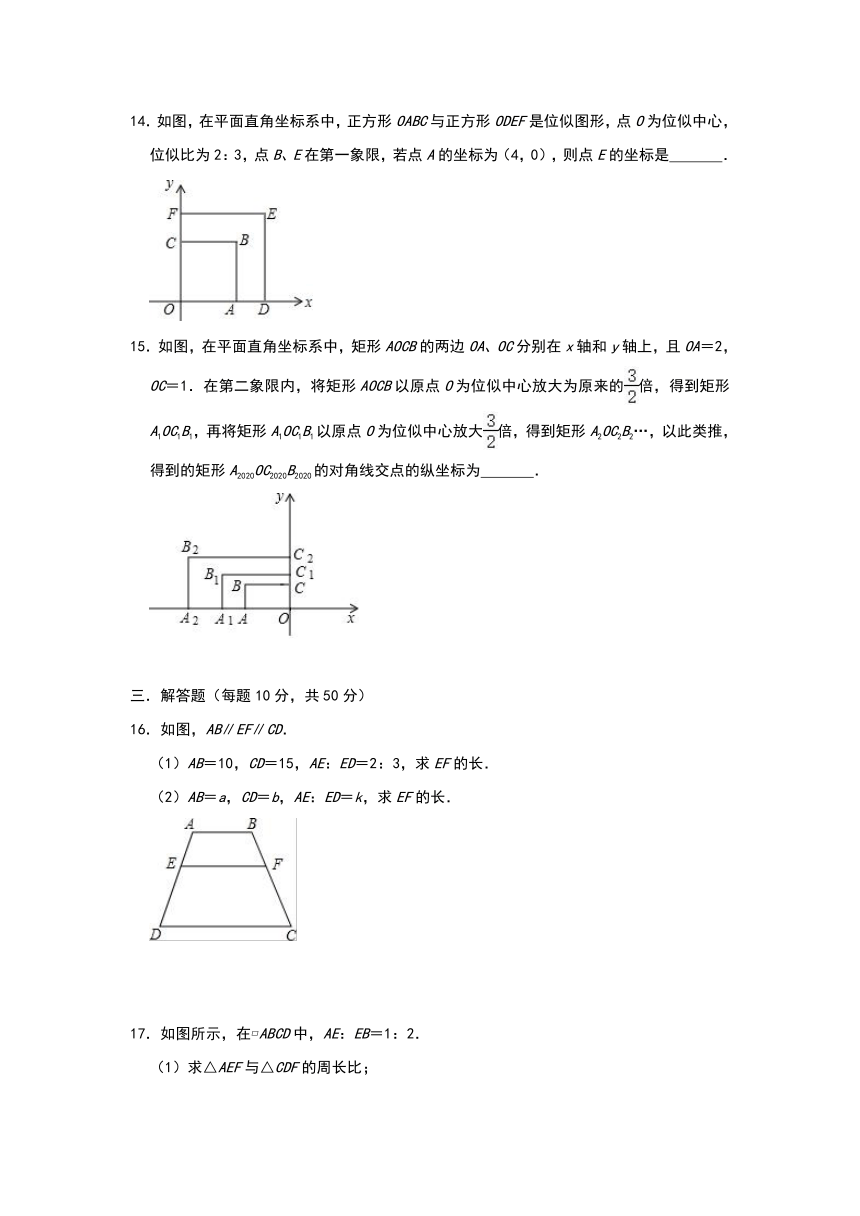
14.如图,在平面直角坐标系中,正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为2:3,点B、E在第一象限,若点A的坐标为(4,0),则点E的坐标是 .
15.如图,在平面直角坐标系中,矩形AOCB的两边OA、OC分别在x轴和y轴上,且OA=2,OC=1.在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大倍,得到矩形A2OC2B2…,以此类推,得到的矩形A2020OC2020B2020的对角线交点的纵坐标为 .
三.解答题(每题10分,共50分)
16.如图,AB∥EF∥CD.
(1)AB=10,CD=15,AE:ED=2:3,求EF的长.
(2)AB=a,CD=b,AE:ED=k,求EF的长.
17.如图所示,在?ABCD中,AE:EB=1:2.
(1)求△AEF与△CDF的周长比;
(2)如果S△AEF=6cm2,求S△CDF和S△ADF.
18.如图,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡在点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处.点E到地面的高度DE=3.5m,点F到地面的高度CF=1.5m,灯泡到木板的水平距离AC=5.4m,墙到木板的水平距离为CD=4m.已知光在镜面反射中的入射角等于反射角,图中点A、B、C、D在同一水平面上.
(1)求BC的长.
(2)求灯泡到地面的高度AG.
19.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),在建立的平面直角坐标系中,△ABC绕旋转中心P逆时针旋转90°后得到△A1B1C1.
(1)在图中标示出旋转中心P,并写出它的坐标;
(2)以原点O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2,在图中画出△A2B2C2,并写出C2的坐标.
20.如图,在矩形ABCD中,AB=6cm,BC=8cm,动点P以2cm/s的速度从点A出发,沿AC向点C移动,同时动点Q以1cm/s的速度从点C出发.沿CB向点B移动,设P、Q两点移动ts(0<t<5)后,△CQP的面积为Scm2
(1)在P、Q两点移动的过程中,△CQP的面积能否等于3.6cm2?若能,求出此时t的值;若不能,请说明理由;
(2)当运动时间为多少秒时,△CPQ与△CAB相似.
参考答案
一.选择题
1.解:∵DE∥AB,
∴△CED∽△CAB,
∴=,即=,
解得,AB=9,
故选:B.
2.解:两个直角三角形不一定相似;
因为只有一个直角相等,
∴A不一定相似;
有有一个角为110°的两个等腰三角形一定相似;
因为110°的角只能是顶角,
所以两个等腰三角形的顶角和底角分别相等,
∴B一定相似;
一个角为55°的两个等腰三角形不一定相似;
因为55°的角可能是顶角,也可能是底角,
∴C不一定相似;
两条边对应成比例,一个对应角相等的两个三角形不一定相似;
因为这个对应角不一定是夹角;
∴D不一定相似;
故选:B.
3.解:若b是a、c的比例中项,
即b2=ac.
42=2c,
解得c=8,
故选:A.
4.解:∵,
∴DE∥BC,
∵,
∴DE∥BC,
∵,
∴DE∥BC,
故选:B.
5.解:∵AB∥CD∥EF,AC=2,AE=5,BD=1.5,
∴,
即,
解得:DF=,
∴BF=BD+DF=,
故选:D.
6.解:
∵在?ABCD中,EM∥AD
∴易证四边形AMEN为平行四边形
∴易证△BEM∽△BAD∽△END
∴==,A项错误
=,B项错误
==,C项错误
==,D项正确
故选:D.
7.解:∵以点O为位似中心,把△ABC放大为原图形的2倍得到△A′B′C′,
∴△ABC∽△A′B′C′,点C、点O、点C′三点在同一直线上,AB∥A′B′,
AO:OA′=1:2,故选项C错误,符合题意.
故选:C.
8.解:设AF=x,则AC=3x,
∵四边形CDEF为正方形,
∴EF=CF=2x,EF∥BC,
∴△AEF∽△ABC,
∴==,
∴BC=6x,
在Rt△ABC中,AB2=AC2+BC2,即302=(3x)2+(6x)2,
解得,x=2,
∴AC=6,BC=12,
∴剩余部分的面积=×12×6﹣4×4=100(cm2),
故选:A.
9.解:∵四边形ABCD是菱形,
∴AB=BC,∠ACB=∠ACD,
∵∠BAC=∠EAF=60°,
∴∠BAE=∠CAF,△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∴∠ACD=∠ACB=60°,
∴∠ABE=∠ACF,
在△BAE和△CAF中,
,
∴△BAE≌△CAF(SAS),
∴AE=AF,BE=CF.故①正确;
∵∠EAF=60°,
∴△AEF是等边三角形,
∴∠AEF=60°,
∵∠AEB+∠CEF=∠AEB+∠EAB=60°,
∴∠EAB=∠CEF,故②正确;
∵∠ACD=∠ACB=60°,
∴∠ECF=60°,
∵∠AEB<60°,
∴△ABE和△EFC不会相似,故③不正确;
过点A作AG⊥BC于点G,过点F作FH⊥EC于点H,
∵∠EAB=15°,∠ABC=60°,
∴∠AEB=45°,
在Rt△AGB中,∵∠ABC=60°,AB=4,
∴BG=2,AG=2,
在Rt△AEG中,∵∠AEG=∠EAG=45°,
∴AG=GE=2,
∴EB=EG﹣BG=2﹣2,
∵△AEB≌△AFC,
∴∠ABE=∠ACF=120°,EB=CF=2﹣2,
∴∠FCE=60°,
在Rt△CHF中,∵∠CFH=30°,CF=2﹣2,
∴CH=﹣1.
∴FH=(﹣1)=3﹣.
∴点F到BC的距离为3﹣,故④不正确.
综上,正确结论的个数是2个,
故选:B.
10.解:∵四边形EFGB是正方形,EB=2,
∴FG=BE=2,∠FGB=90°,
∵四边形ABCD是正方形,H为AD的中点,
∴AD=4,AH=2,
∠BAD=90°,
∴∠HAN=∠FGN,AH=FG,
∵∠ANH=∠GNF,
∴△ANH≌△GNF(AAS),故①正确;
∴∠AHN=∠HFG,
∵AG=FG=2=AH,
∴AF=FG=AH,
∴∠AFH≠∠AHF,
∴∠AFN≠∠HFG,故②错误;
∵△ANH≌△GNF,
∴AN=AG=1,
∵GM=BC=4,
∴==2,
∵∠HAN=∠AGM=90°,
∴△AHN∽△GMA,
∴∠AHN=∠AMG,
∵AD∥GM,
∴∠HAK=∠AMG,
∴∠AHK=∠HAK,
∴AK=HK,
∴AK=HK=NK,
∵FN=HN,
∴FN=2NK;故③正确;
∵延长FG交DC于M,
∴四边形ADMG是矩形,
∴DM=AG=2,
∵S△AFN=AN?FG=2×1=1,S△ADM=AD?DM=×4×2=4,
∴S△AFN:S△ADM=1:4故④正确,
故选:C.
二.填空题(共5小题)
11.解:根据黄金分割定义可知:
∵BP2=AB?AP,
设AB为1,则AP=1﹣BP,
∴BP2=1?(1﹣BP)
BP2+BP﹣1=0,
解得BP=(舍去)
∴BP=.
故答案为.
12.解:∵AD=DC=5,AB=10,∠A=90°,
∴BD==5,
∵∠ADB=∠CDE,∠A=∠E=90°,
∴△ABD∽△ECD,
∴=,
∴=,
∴DE=,
∴BE=BD+DE=6,
故答案为6.
13.解:如图,设直线l与AB、CD分别交于点E、D,
则由“完美分割线”的定义可知,S△AED=S四边形BCDE,
∴=,
∵l∥BC,
∴△AED∽△ABC,
∴===,
设AE=AD=x,
则=,
∴x=,
∴BE=CD=2﹣,
∴BC=2﹣2(2﹣)=4﹣4.
14.解:∵正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为2:3,
∴=,=,即=,=,
解得,OD=6,OF=6,
则点E的坐标为(6,6),
故答案为:(6,6).
15.解:∵四边形AOCB为矩形,OA=2,OC=1,
∴矩形AOCB的对角线交点的纵坐标为,
∵在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的倍,
∴矩形A1OC1B1的对角线交点的纵坐标为×,
…
∴矩形A2020OC2020B2020的对角线交点的纵坐标为×()2020=,
故答案为:.
三.解答题(共5小题)
16.解:(1)过点A作AN∥BC交CD于N,交EF于M,如图,
∵AB∥EF∥DC,
∴四边形AMFB、四边形MNCF都为平行四边形,
∴AB=MF=NC=10,
∴DN=CD﹣CN=15﹣10=5,
∵EM∥DN,
∴==,
∴EM=×5=2,
∴EF=EM+MF=2+10=12;
(2)∵四边形AMFB、四边形MNCF都为平行四边形,
∴AB=MF=NC=a,
∴DN=CD﹣CN=a﹣b,
∵EM∥DN,
∴==,
∴EM=DN=(a﹣b),
∴EF=EM+MF=(a﹣b)+a=.
17.解:(1)∵AE:EB=1:2,
∴AE:AB=1:3,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴△AEF∽△CDF
∴C△AEF:C△CDF=EF:DF=AE:CD=AE:AB=1:3,
即△AEF与△CDF的周长比为1:3;
(2)∵△AEF∽△CDF,
∴S△AEF:S△CDF=(AE:CD)2,
即6:S△CDF=(1:3)2
∴S△CDF=6×9=54 cm2.
∵==,
∴S△ADF=3×6=18(cm2).
18.解:(1)由题意可得:FC∥DE,
则△BFC∽BED,
故,
即,
解得:BC=3;
(2)∵AC=5.4m,
∴AB=5.4﹣3=2.4(m),
∵光在镜面反射中的入射角等于反射角,
∴∠FBC=∠GBA,
又∵∠FCB=∠GAB,
∴△BGA∽△BFC,
∴=,
∴,
解得:AG=1.2(m),
答:灯泡到地面的高度AG为1.2m.
19.解:(1)如图,点P为所作,P点坐标为(3,1);
(2)如图,△A2B2C2为所作,C2的坐标为(2,4)或(﹣2,﹣4).
20.解:(1)在矩形ABCD中,
∵AB=6cm,BC=8cm,
∴AC=10cm,AP=2tcm,PC=(10﹣2t)cm,
CQ=tcm,
过点P作PH⊥BC于点H,
则PH=(10﹣2t)cm,
根据题意,得 t?(10﹣2t)=3.6,
解得:t1=2,t2=3.
答:△CQP的面积等于3.6cm2时,t的值为2或3.
(2)如答图1,当∠PQC=90°时,PQ⊥BC,
∵AB⊥BC,AB=6,BC=8,QC=t,PC=10﹣2t,
∴△PQC∽△ABC,
∴=,即=,解得t=(秒);
如答图2,当∠CPQ=90°时,PQ⊥AC,
∵∠ACB=∠QCP,∠B=∠QPC,
∴△CPQ∽△CBA,
∴=,即=,解得t=(秒).
综上所述,t为秒与秒时,△CPQ与△CAB相似.
单元培优测试卷
一.选择题(每题3分,共30分)
1.如图,DE∥AB,如果CE:AE=1:2,DE=3,那么AB等于( )
A.6 B.9 C.12 D.13
2.分别画出下列四组图形,必是相似三角形的为( )
A.两个直角三角形
B.有一个角为110°的两个等腰三角形
C.有一个角为55°的两个等腰三角形
D.两条边对应成比例,其中一边的对角对应相等的两个三角形
3.已知线段a=2,b=4,如果线段b是线段a和c的比例中项,那么线段c的长度是( )
A.8 B.6 C. D.2
4.如图,点D、E分别在△ABC的边AB、AC上,下列各比例式不一定能推得DE∥BC的是( )
A.= B.= C.= D.=
5.如图,AB∥CD∥EF,AC=2,AE=5,BD=1.5,那么下列结论正确的是( )
A.DF= B.EF= C.CD= D.BF=
6.如图,在?ABCD中,点E在对角线BD上,EM∥AD,交AB于点M,EN∥AB,交AD于点N,则下列式子一定正确的是( )
A.= B.= C.= D.=
7.如图,以点O为位似中心,把△ABC放大为原图形的2倍得到△A′B′C′,以下说法中错误的是( )
A.△ABC∽△A′B′C′
B.点C、点O、点C′三点在同一直线上
C.AO:AA′=1:2
D.AB∥A′B′
8.如图,在一块斜边长30cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上,若AF:AC=1:3,则这块木板截取正方形CDEF后,剩余部分的面积为( )
A.100cm2 B.150cm2 C.170cm2 D.200cm2
9.如图,在菱形ABCD中,已知AB=4,∠ABC=60°,∠EAF=60°,点E在CB的延长线上,点F在DC的延长线上,有下列结论:
①BE=CF;②∠EAB=∠CEF;③△ABE∽△EFC;④若∠BAE=15°,则点F到BC的距离为2﹣2.
则其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
10.如图,正方形ABCD的边长为4,延长CB至E使EB=2,以EB为边在上方作正方形EFGB,延长FG交DC于M,连接AM,AF,H为AD的中点,连接FH分别与AB,AM交于点N、K:则下列结论:
①△ANH≌△GNF;
②∠AFN=∠HFG;
③FN=2NK;
④S△AFN:S△ADM=1:4.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(每题4分,共20分)
11.已知点P在线段AB上,且满足BP2=AB?AP,则的值等于 .
12.如图,AC与BE交于点D,∠A=∠E=90°,若点D是线段AC的中点,且AB=AC=10.则BE的长等于 .
13.如果直线l把△ABC分割后的两个部分面积相等,且周长也相等,那么就把直线l叫做△ABC的“完美分割线”,已知在△ABC中,AB=AC,△ABC的一条“完美分割线”为直线l,且直线l平行于BC,若AB=2,则BC的长等于 .
14.如图,在平面直角坐标系中,正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为2:3,点B、E在第一象限,若点A的坐标为(4,0),则点E的坐标是 .
15.如图,在平面直角坐标系中,矩形AOCB的两边OA、OC分别在x轴和y轴上,且OA=2,OC=1.在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大倍,得到矩形A2OC2B2…,以此类推,得到的矩形A2020OC2020B2020的对角线交点的纵坐标为 .
三.解答题(每题10分,共50分)
16.如图,AB∥EF∥CD.
(1)AB=10,CD=15,AE:ED=2:3,求EF的长.
(2)AB=a,CD=b,AE:ED=k,求EF的长.
17.如图所示,在?ABCD中,AE:EB=1:2.
(1)求△AEF与△CDF的周长比;
(2)如果S△AEF=6cm2,求S△CDF和S△ADF.
18.如图,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡在点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处.点E到地面的高度DE=3.5m,点F到地面的高度CF=1.5m,灯泡到木板的水平距离AC=5.4m,墙到木板的水平距离为CD=4m.已知光在镜面反射中的入射角等于反射角,图中点A、B、C、D在同一水平面上.
(1)求BC的长.
(2)求灯泡到地面的高度AG.
19.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),在建立的平面直角坐标系中,△ABC绕旋转中心P逆时针旋转90°后得到△A1B1C1.
(1)在图中标示出旋转中心P,并写出它的坐标;
(2)以原点O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2,在图中画出△A2B2C2,并写出C2的坐标.
20.如图,在矩形ABCD中,AB=6cm,BC=8cm,动点P以2cm/s的速度从点A出发,沿AC向点C移动,同时动点Q以1cm/s的速度从点C出发.沿CB向点B移动,设P、Q两点移动ts(0<t<5)后,△CQP的面积为Scm2
(1)在P、Q两点移动的过程中,△CQP的面积能否等于3.6cm2?若能,求出此时t的值;若不能,请说明理由;
(2)当运动时间为多少秒时,△CPQ与△CAB相似.
参考答案
一.选择题
1.解:∵DE∥AB,
∴△CED∽△CAB,
∴=,即=,
解得,AB=9,
故选:B.
2.解:两个直角三角形不一定相似;
因为只有一个直角相等,
∴A不一定相似;
有有一个角为110°的两个等腰三角形一定相似;
因为110°的角只能是顶角,
所以两个等腰三角形的顶角和底角分别相等,
∴B一定相似;
一个角为55°的两个等腰三角形不一定相似;
因为55°的角可能是顶角,也可能是底角,
∴C不一定相似;
两条边对应成比例,一个对应角相等的两个三角形不一定相似;
因为这个对应角不一定是夹角;
∴D不一定相似;
故选:B.
3.解:若b是a、c的比例中项,
即b2=ac.
42=2c,
解得c=8,
故选:A.
4.解:∵,
∴DE∥BC,
∵,
∴DE∥BC,
∵,
∴DE∥BC,
故选:B.
5.解:∵AB∥CD∥EF,AC=2,AE=5,BD=1.5,
∴,
即,
解得:DF=,
∴BF=BD+DF=,
故选:D.
6.解:
∵在?ABCD中,EM∥AD
∴易证四边形AMEN为平行四边形
∴易证△BEM∽△BAD∽△END
∴==,A项错误
=,B项错误
==,C项错误
==,D项正确
故选:D.
7.解:∵以点O为位似中心,把△ABC放大为原图形的2倍得到△A′B′C′,
∴△ABC∽△A′B′C′,点C、点O、点C′三点在同一直线上,AB∥A′B′,
AO:OA′=1:2,故选项C错误,符合题意.
故选:C.
8.解:设AF=x,则AC=3x,
∵四边形CDEF为正方形,
∴EF=CF=2x,EF∥BC,
∴△AEF∽△ABC,
∴==,
∴BC=6x,
在Rt△ABC中,AB2=AC2+BC2,即302=(3x)2+(6x)2,
解得,x=2,
∴AC=6,BC=12,
∴剩余部分的面积=×12×6﹣4×4=100(cm2),
故选:A.
9.解:∵四边形ABCD是菱形,
∴AB=BC,∠ACB=∠ACD,
∵∠BAC=∠EAF=60°,
∴∠BAE=∠CAF,△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∴∠ACD=∠ACB=60°,
∴∠ABE=∠ACF,
在△BAE和△CAF中,
,
∴△BAE≌△CAF(SAS),
∴AE=AF,BE=CF.故①正确;
∵∠EAF=60°,
∴△AEF是等边三角形,
∴∠AEF=60°,
∵∠AEB+∠CEF=∠AEB+∠EAB=60°,
∴∠EAB=∠CEF,故②正确;
∵∠ACD=∠ACB=60°,
∴∠ECF=60°,
∵∠AEB<60°,
∴△ABE和△EFC不会相似,故③不正确;
过点A作AG⊥BC于点G,过点F作FH⊥EC于点H,
∵∠EAB=15°,∠ABC=60°,
∴∠AEB=45°,
在Rt△AGB中,∵∠ABC=60°,AB=4,
∴BG=2,AG=2,
在Rt△AEG中,∵∠AEG=∠EAG=45°,
∴AG=GE=2,
∴EB=EG﹣BG=2﹣2,
∵△AEB≌△AFC,
∴∠ABE=∠ACF=120°,EB=CF=2﹣2,
∴∠FCE=60°,
在Rt△CHF中,∵∠CFH=30°,CF=2﹣2,
∴CH=﹣1.
∴FH=(﹣1)=3﹣.
∴点F到BC的距离为3﹣,故④不正确.
综上,正确结论的个数是2个,
故选:B.
10.解:∵四边形EFGB是正方形,EB=2,
∴FG=BE=2,∠FGB=90°,
∵四边形ABCD是正方形,H为AD的中点,
∴AD=4,AH=2,
∠BAD=90°,
∴∠HAN=∠FGN,AH=FG,
∵∠ANH=∠GNF,
∴△ANH≌△GNF(AAS),故①正确;
∴∠AHN=∠HFG,
∵AG=FG=2=AH,
∴AF=FG=AH,
∴∠AFH≠∠AHF,
∴∠AFN≠∠HFG,故②错误;
∵△ANH≌△GNF,
∴AN=AG=1,
∵GM=BC=4,
∴==2,
∵∠HAN=∠AGM=90°,
∴△AHN∽△GMA,
∴∠AHN=∠AMG,
∵AD∥GM,
∴∠HAK=∠AMG,
∴∠AHK=∠HAK,
∴AK=HK,
∴AK=HK=NK,
∵FN=HN,
∴FN=2NK;故③正确;
∵延长FG交DC于M,
∴四边形ADMG是矩形,
∴DM=AG=2,
∵S△AFN=AN?FG=2×1=1,S△ADM=AD?DM=×4×2=4,
∴S△AFN:S△ADM=1:4故④正确,
故选:C.
二.填空题(共5小题)
11.解:根据黄金分割定义可知:
∵BP2=AB?AP,
设AB为1,则AP=1﹣BP,
∴BP2=1?(1﹣BP)
BP2+BP﹣1=0,
解得BP=(舍去)
∴BP=.
故答案为.
12.解:∵AD=DC=5,AB=10,∠A=90°,
∴BD==5,
∵∠ADB=∠CDE,∠A=∠E=90°,
∴△ABD∽△ECD,
∴=,
∴=,
∴DE=,
∴BE=BD+DE=6,
故答案为6.
13.解:如图,设直线l与AB、CD分别交于点E、D,
则由“完美分割线”的定义可知,S△AED=S四边形BCDE,
∴=,
∵l∥BC,
∴△AED∽△ABC,
∴===,
设AE=AD=x,
则=,
∴x=,
∴BE=CD=2﹣,
∴BC=2﹣2(2﹣)=4﹣4.
14.解:∵正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为2:3,
∴=,=,即=,=,
解得,OD=6,OF=6,
则点E的坐标为(6,6),
故答案为:(6,6).
15.解:∵四边形AOCB为矩形,OA=2,OC=1,
∴矩形AOCB的对角线交点的纵坐标为,
∵在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的倍,
∴矩形A1OC1B1的对角线交点的纵坐标为×,
…
∴矩形A2020OC2020B2020的对角线交点的纵坐标为×()2020=,
故答案为:.
三.解答题(共5小题)
16.解:(1)过点A作AN∥BC交CD于N,交EF于M,如图,
∵AB∥EF∥DC,
∴四边形AMFB、四边形MNCF都为平行四边形,
∴AB=MF=NC=10,
∴DN=CD﹣CN=15﹣10=5,
∵EM∥DN,
∴==,
∴EM=×5=2,
∴EF=EM+MF=2+10=12;
(2)∵四边形AMFB、四边形MNCF都为平行四边形,
∴AB=MF=NC=a,
∴DN=CD﹣CN=a﹣b,
∵EM∥DN,
∴==,
∴EM=DN=(a﹣b),
∴EF=EM+MF=(a﹣b)+a=.
17.解:(1)∵AE:EB=1:2,
∴AE:AB=1:3,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴△AEF∽△CDF
∴C△AEF:C△CDF=EF:DF=AE:CD=AE:AB=1:3,
即△AEF与△CDF的周长比为1:3;
(2)∵△AEF∽△CDF,
∴S△AEF:S△CDF=(AE:CD)2,
即6:S△CDF=(1:3)2
∴S△CDF=6×9=54 cm2.
∵==,
∴S△ADF=3×6=18(cm2).
18.解:(1)由题意可得:FC∥DE,
则△BFC∽BED,
故,
即,
解得:BC=3;
(2)∵AC=5.4m,
∴AB=5.4﹣3=2.4(m),
∵光在镜面反射中的入射角等于反射角,
∴∠FBC=∠GBA,
又∵∠FCB=∠GAB,
∴△BGA∽△BFC,
∴=,
∴,
解得:AG=1.2(m),
答:灯泡到地面的高度AG为1.2m.
19.解:(1)如图,点P为所作,P点坐标为(3,1);
(2)如图,△A2B2C2为所作,C2的坐标为(2,4)或(﹣2,﹣4).
20.解:(1)在矩形ABCD中,
∵AB=6cm,BC=8cm,
∴AC=10cm,AP=2tcm,PC=(10﹣2t)cm,
CQ=tcm,
过点P作PH⊥BC于点H,
则PH=(10﹣2t)cm,
根据题意,得 t?(10﹣2t)=3.6,
解得:t1=2,t2=3.
答:△CQP的面积等于3.6cm2时,t的值为2或3.
(2)如答图1,当∠PQC=90°时,PQ⊥BC,
∵AB⊥BC,AB=6,BC=8,QC=t,PC=10﹣2t,
∴△PQC∽△ABC,
∴=,即=,解得t=(秒);
如答图2,当∠CPQ=90°时,PQ⊥AC,
∵∠ACB=∠QCP,∠B=∠QPC,
∴△CPQ∽△CBA,
∴=,即=,解得t=(秒).
综上所述,t为秒与秒时,△CPQ与△CAB相似.
