2020--2021学年人教版九年级数学下册 第 二十七 章相似重点题型专题练习(word解析版)
文档属性
| 名称 | 2020--2021学年人教版九年级数学下册 第 二十七 章相似重点题型专题练习(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 326.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-27 12:17:30 | ||
图片预览


文档简介
九年级数学下册 第 二十七 章《相似》
重点题型专题练习(二)
一.选择题
1.已知=2,则的值是( )
A. B.﹣ C.3 D.﹣3
2.如图,已知AD∥BE∥CF,那么下列结论正确的是( )
A.= B.= C.= D.=
3.如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,点A,B,E在x轴上.若正方形ABCD的边长为2,则点F坐标为( )
A.(8,6) B.(9,6) C. D.(10,6)
4.如图,在△ABC中,DE∥AB,且,则的值为( )
A. B. C. D.
5.如图,下列条件中不能判定△ACD∽△ABC的是( )
A.∠ADC=∠ACB B. C.∠ACD=∠B D.AC2=AD?AB
6.若如图所示的两个四边形相似,则∠α的度数是( )
A.75° B.60° C.87° D.120°
7.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中第九卷《勾股》章,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑,东西七里,南北九里,各中开门,出东门一十五里有木,问:出南门几何步而见木?”
译文:“今有一座长方形小城,东西向城墙长7里,南北向城墙长9里,各城墙正中均开一城门.走出东门15里处有棵大树,问走出南门多少步恰好能望见这棵树?”(注:1里=300步)
你的计算结果是:出南门几何步而见木( )
A.300步 B.315 步 C.400 步 D.415步
8.如图,顽皮的小聪在小芳的作业本上用红笔画了个“×”(作业本中的横格线都平行,且相邻两条横格线间的距离都相等),A、B、C、D、O都在横格线上,且线段AD、BC交于点O.若线段AB=4cm,则线段CD长为( )
A.4cm B.5cm C.6cm D.8cm
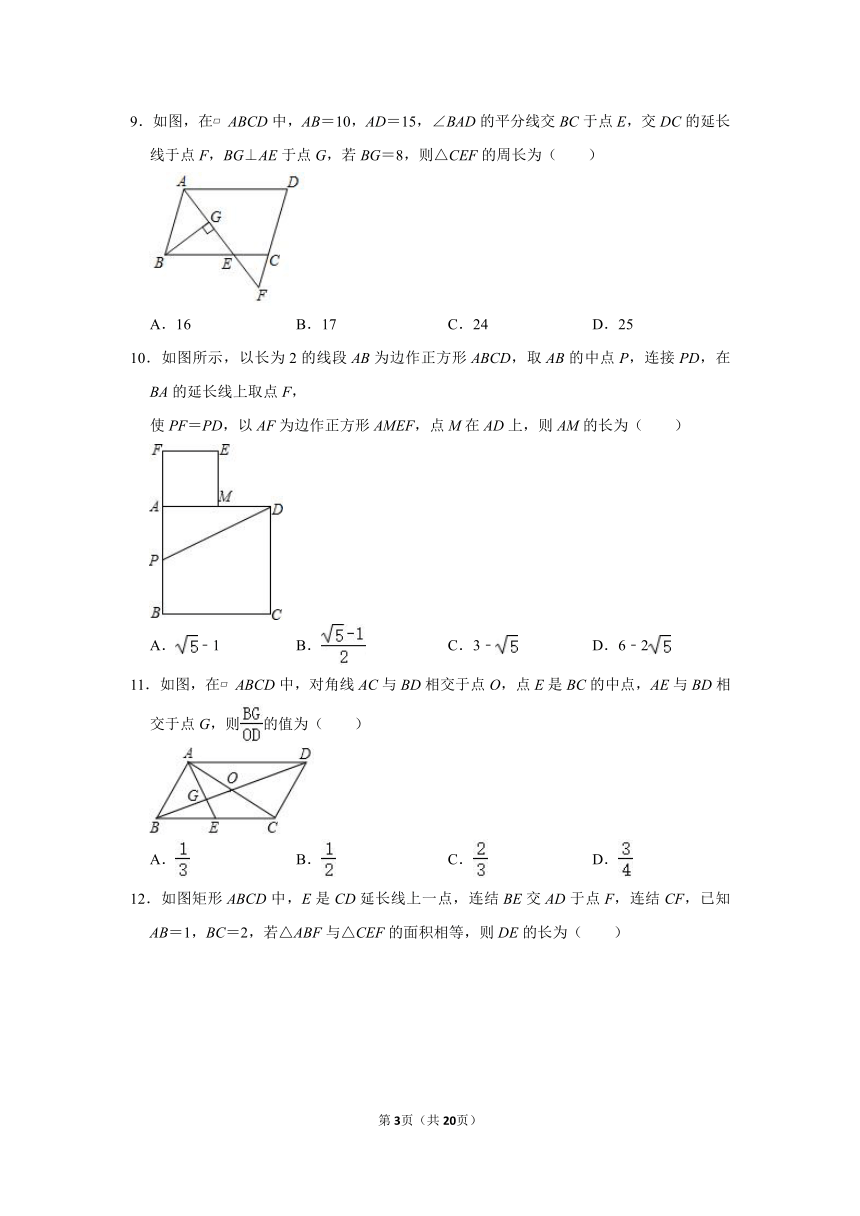
9.如图,在?ABCD中,AB=10,AD=15,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,若BG=8,则△CEF的周长为( )
A.16 B.17 C.24 D.25
10.如图所示,以长为2的线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,
使PF=PD,以AF为边作正方形AMEF,点M在AD上,则AM的长为( )
A.﹣1 B. C.3﹣ D.6﹣2
11.如图,在?ABCD中,对角线AC与BD相交于点O,点E是BC的中点,AE与BD相交于点G,则的值为( )
A. B. C. D.
12.如图矩形ABCD中,E是CD延长线上一点,连结BE交AD于点F,连结CF,已知AB=1,BC=2,若△ABF与△CEF的面积相等,则DE的长为( )
A.1 B. C. D.
二.填空题
13.如果=,那么的值等于 .
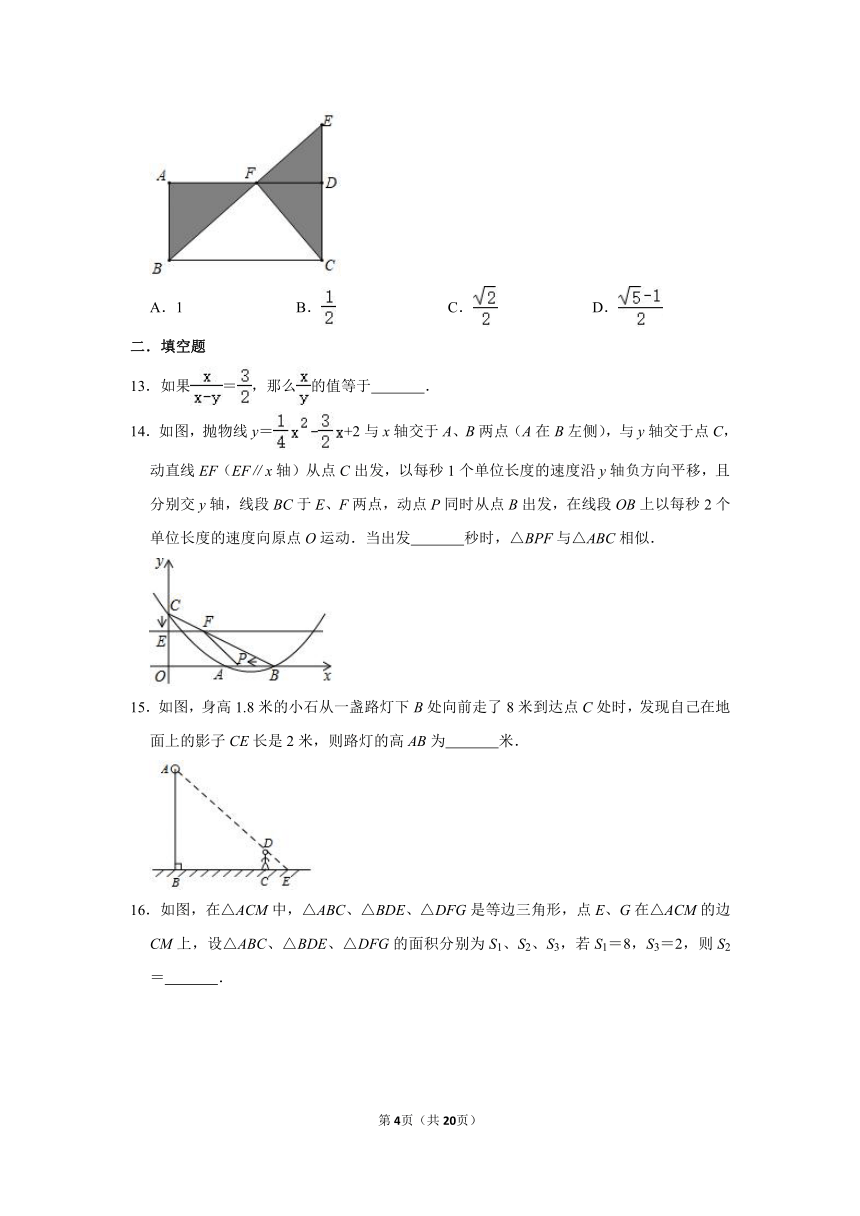
14.如图,抛物线y=+2与x轴交于A、B两点(A在B左侧),与y轴交于点C,动直线EF(EF∥x轴)从点C出发,以每秒1个单位长度的速度沿y轴负方向平移,且分别交y轴,线段BC于E、F两点,动点P同时从点B出发,在线段OB上以每秒2个单位长度的速度向原点O运动.当出发 秒时,△BPF与△ABC相似.
15.如图,身高1.8米的小石从一盏路灯下B处向前走了8米到达点C处时,发现自己在地面上的影子CE长是2米,则路灯的高AB为 米.
16.如图,在△ACM中,△ABC、△BDE、△DFG是等边三角形,点E、G在△ACM的边CM上,设△ABC、△BDE、△DFG的面积分别为S1、S2、S3,若S1=8,S3=2,则S2= .
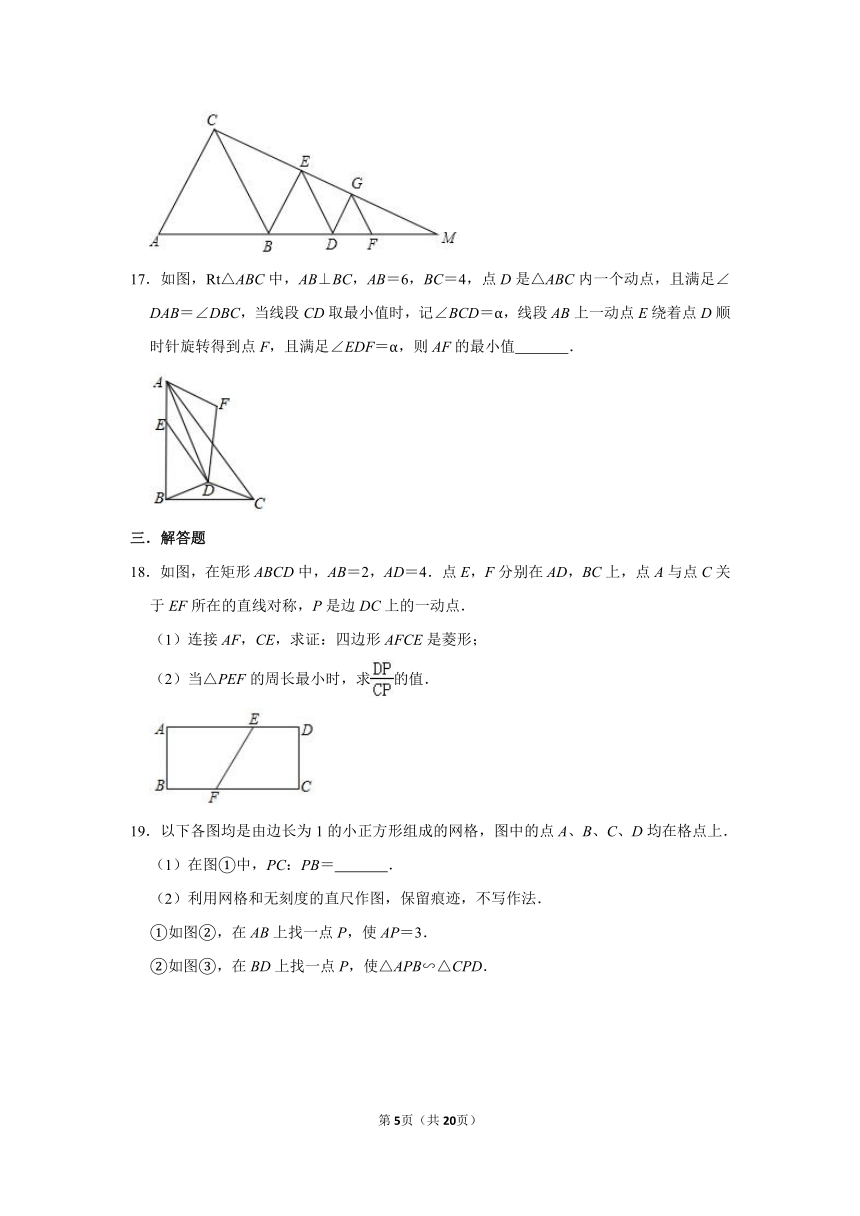
17.如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,点D是△ABC内一个动点,且满足∠DAB=∠DBC,当线段CD取最小值时,记∠BCD=α,线段AB上一动点E绕着点D顺时针旋转得到点F,且满足∠EDF=α,则AF的最小值 .
三.解答题
18.如图,在矩形ABCD中,AB=2,AD=4.点E,F分别在AD,BC上,点A与点C关于EF所在的直线对称,P是边DC上的一动点.
(1)连接AF,CE,求证:四边形AFCE是菱形;
(2)当△PEF的周长最小时,求的值.
19.以下各图均是由边长为1的小正方形组成的网格,图中的点A、B、C、D均在格点上.
(1)在图①中,PC:PB= .
(2)利用网格和无刻度的直尺作图,保留痕迹,不写作法.
①如图②,在AB上找一点P,使AP=3.
②如图③,在BD上找一点P,使△APB∽△CPD.
20.如图,在正方形ABCD中,在BC边上取中点E,连接DE,过点E做EF⊥ED交AB于点G、交AD延长线于点F.
(1)求证:△ECD∽△DEF;
(2)若CD=4,求AF的长.
21.如图,△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD,CE交于点F,连接DE.
(1)求证:△ABD∽△ACE;
(2)求证:△ADE∽△ABC;
(3)若BE=CE=,CD=1,求DF的长.
22.如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B.
(1)判定△ABP与△PCD是否相似,说明理由;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.
23.已知:△ABC中,D为BC的中点,E为AB上一点,且BE=AB.F为AC上一点,且CF=AC,EF交AD于P.
(1)求EP:PF的值.
(2)求AP:PD的值.
24.已知,矩形ABCD,点E是AD上一点,将矩形沿BE折叠,点A恰好落在BD上点F处.
(1)如图1,若AB=3,AD=4,求AE的长;
(2)如图2,若点F恰好是BD的中点,点M是BD上一点,过点M作MN∥BE交AD于点N,连接EM,若MN平分∠EMD,求证:DN?DE=DM?BM.
参考答案
一.选择题
1.解:∵=2,
∴b=2a,
∴==﹣.
故选:B.
2.解:∵AD∥BE∥CF,
∴,,
故A、D、C错误,B正确.
故选:B.
3.解:∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,
∴==,
∵BC=2,
∴EF=BE=6,
∵BC∥EF,
∴△OBC∽△OEF,
∴=,
解得:OB=3,
∴EO=9,
∴F点坐标为:(9,6),
故选:B.
4.解:∵=,
∴=,
∵DE∥AB,
∴==,
故选:A.
5.解:A、由∠ADC=∠ACB,∠A=∠A可得△ACD∽△ABC,此选项不符合题意;
B、由不能判定△ACD∽△ABC,此选项符合题意;
C、由∠ACD=∠B,∠A=∠A可得△ACD∽△ABC,此选项不符合题意;
D、由AC2=AD?AB,即=,且∠A=∠A可得△ACD∽△ABC,此选项不符合题意;
故选:B.
6.解:根据相似多边形的特点可知对应角相等,所以∠α=360°﹣60°﹣138°﹣75°=87°.故选C.
7.解:由题意得,AB=15里,AC=4.5里,CD=3.5里,
△ACB∽△DEC,
∴=,即=,
解得,DE=1.05里=315步,
∴走出南门315步恰好能望见这棵树,
故选:B.
8.解:如图,过点O作OE⊥AB于点E,OF⊥CD于点F,则OE、OF分别是△AOB、△DOC的高线,
∵练习本中的横格线都平行,
∴△AOB∽△DOC,
∴=,即=,
∴CD=6cm.
故选:C.
9.解:∵在?ABCD中,CD=AB=10,BC=AD=15,∠BAD的平分线交BC于点E,
∴AB∥DC,∠BAF=∠DAF,
∴∠BAF=∠F,
∴∠DAF=∠F,
∴DF=AD=15,
同理BE=AB=10,
∴CF=DF﹣CD=15﹣10=5;
∴在△ABG中,BG⊥AE,AB=10,BG=8,
在Rt△ABG中,AG===6,
∴AE=2AG=12,
∴△ABE的周长等于10+10+12=32,
∵四边形ABCD是平行四边形,
∴AB∥CF,
∴△CEF∽△BEA,相似比为5:10=1:2,
∴△CEF的周长为16.
故选:A.
10.解:在Rt△APD中,AP=1,AD=2,
由勾股定理知PD===,
∴AM=AF=PF﹣AP=PD﹣AP=﹣1.
故选:A.
11.解:∵点E是BC的中点,
∴BC=2BE,
∵四边形ABCD是平行四边形,
∴OB=OD,AD=BC=2BE,AD∥BC,
∴△BEG∽△DAG,
∴==,
∴DG=2BG,
∴BD=3BG,OD=OB=BG,
∴=;
故选:C.
12.解:设DE=x.
∵DF∥BC,
∴△EFD∽△EBC,
∴=,
∴=,
∴DF=,AF=2﹣=,
∵△ABF与△CEF的面积相等,
∴?AF?AB=?EC?DF,
∴×1=×(x+1),
∴解得x=或(舍弃),
故选:D.
二.填空题(共5小题)
13.解:∵=,
∴3x﹣3y=2x,
故x=3y
∴=3.
故答案为:3.
14.解:∵抛物线y=x+2与x轴交于A、B两点(A在B左侧),与y轴交于点C,
∴令y=0,得x+2=0,解得x=2或x=4,
∴A(2,0),B(4,0),
当x=0时,y=2,
∴C(0,2),
在Rt△BOC中,OC=2,OB=4,
∴BC===2,
∵EF∥OB,
∴,
∴,
∴BF=(2﹣t),
BP=2t(0<t≤2).
①当FP∥AC时,△BFP∽△BCA,
∴,
∴,
解得t=.
②当时,△BFP∽△BAC,
∴,
解得t=,
综上所述,满足条件的t的值为s或s.
故答案为:或.
15.解:由题意知,CE=2米,CD=1.8米,BC=8米,CD∥AB,
则BE=BC+CE=10米,
∵CD∥AB,
∴△ECD∽△EBA
∴=,即=,
解得AB=9(米),
即路灯的高AB为9米;
故答案为:9.
16.解:△ABC、△BDE、△DGF的边长分别是a、b、c,
∵△ABC、△BDE是等边三角形,
∴∠CBA=∠EBD=60°,
∴∠CBE=60°,
同理∠EDG=60°,
∴∠CBE=∠EDG,
∵△BDE、△DGF是等边三角形,
∴∠EBD=∠GDF=60°,
∴BE∥DG,
∴∠CEB=∠EGD,
∴△CBE∽△EDG,
∴a:b=b:c,
∴b2=ac,
∵S1:S3=(a:c)2=8:2=4:1,
∴a:c=2:1,
∵S1:S2=()2====,
∴S2=S1=4.
故答案是4.
17.解:∵AB⊥BC,AB=6、BC=4,
∴∠DBC+∠ABD=90°,
∵∠DAB=∠DBC,设∠DAB=∠DBC=β,
∴∠DAB+∠ABD=90°,
∴∠ADB=90°,
∴点D在以AB为直径的圆上,设圆心为O,半径为AB=3,则当O、D、C三点共线时CD最小,
∴OD=OB=OA=3,
∴OC==5,
将DA绕点D逆时针旋转α,得到DG,连接GE,
∴DG=DA,
∠GDA=∠EDF=α,
∴∠GDE=∠ADF,
∵DE=DF,
∴△GDE≌△ADF(SAS),
∴GE=AF,
∴当GE⊥AB时,GE最小,即AF最小,
过点D作DM⊥AB于M,过点G作GH⊥DM,交DM的延长线于点H,
∴DM∥BC,四边形GHME为矩形.
∴△OMD∽△OBC,GE=HM,
∴,
∴,
∴DM=,OM=,
∴AM=OM+OA=+3=,
∵∠DAB=∠DBC=β,OA=OD,
∴∠ODA=∠OAD=β,
∴∠BOC=∠ODA+∠OAD=2β.
∵在Rt△OBC中,∠OCB=90°﹣∠BOC,
∴α=90°﹣2β,
∵∠MAD+∠MDA=90°,
∴β+α+∠GDH=90°,
∴∠GDH=β=∠DAM,
∵∠DHG=∠AMD=90°,AD=DG,
∴△GDH≌△DAM(AAS).
∴DH=AM=,
∴HM=DH﹣DM=,即AF的最小值为.
故答案为:.
三.解答题(共7小题)
18.解:(1)证明:如图,连接AF,CE,AC交EF于点O
∵四边形ABCD是矩形
∴AB=CD,AD=BC,AD∥BC
∴∠AEO=∠CFO,∠EAO=∠FCO
∵点A与点C关于EF所在的直线对称
∴AO=CO,AC⊥EF
∵∠AEO=∠CFO,∠EAO=∠FCO,AO=CO
∴△AEO≌△CFO(AAS)
∴AE=CF,且AE∥CF
∴四边形AFCE是平行四边形,
又∵AC⊥EF
∴四边形AFCE是菱形;
(2)如图,作点F关于CD的对称点H,连接EH,交CD于点P,此时△PEF的周长最小
∵四边形AFCE是菱形
∴AF=CF=CE=AE
∵AF2=BF2+AB2
∴AF2=(4﹣AF)2+4
∴AF=
∵AD∥BC
∴△DEP∽△CHP
∴==.
答:当△PEF的周长最小时,的值为.
19.解:(1)图1中,
∵AB∥CD,
∴==,
故答案为1:3.
(2)
①如图2所示,点P即为所要找的点;
②如图3所示,作点A的对称点A′,
连接A′C,交BD于点P,
点P即为所要找的点,
∵AB∥CD,
∴△APB∽△CPD.
20.(1)证明:∵四边形ABCD是正方形,EF⊥ED,
∴∠FED=∠C=90°,BC∥AD,
∴∠CED=∠FDE,
∴△ECD∽△DEF;
(2)解:∵四边形ABCD是正方形,
∴∠C=90°,AD=BC=CD=4,
∵E为BC的中点,
∴CE=BC=2,
在Rt△DCE中,由勾股定理得:DE===2,
∵△ECD∽△DEF,
∴=,
∴=,
解得:DF=10,
∵AD=4,
∴AF=DF﹣AD=10﹣4=6.
21.(1)证明;∵BD⊥AC于点D,CE⊥AB于点E,
∴∠ADB=∠AEC=90°,
∵∠A=∠A,
∴△ADB∽△AEC.
(2)证明:∵△ADB∽△AEC,
∴=,
∴=,
∵∠A=∠A,
∴△ADE∽△ABC.
(3)解:过点E作EN⊥ED交BD于N,过点E作EM⊥DN于M.
在Rt△BEC中,∵BE=EC=,∠BEC=90°,
∴BC=BE=,∠BCF=45°,
∵∠BDC=90°,
∴BD===3,
∵∠EFB=∠DFC,∠BEF=∠CDF=90°,
∴△BFE∽△CFD,
∴=,
∴=,
∵∠EFD=∠BFC,
∴△EFD∽△BFC,
∴∠EDF=∠BCF=45°,
∵∠NED=90°,
∴∠END=∠EDN=45°,
∴EN=ED,
∵∠BEC=∠NED=90°,
∴∠BEN=∠CED,
∵BE=CE,
∴△BEN≌△CED(SAS),
∴BN=CD=1,DN=BD﹣BN=2,
∵EN=ED,EM⊥DN,
∴MN=DM=1,
∴EM=MN=MD=1,
∵∠EMF=∠CDF=90°,∠EFM=∠CFD,EM=CD,
∴△EMF≌△CDF(AAS),
∴MF=DF,
∴DF=.
22.解:(1)△BAP∽△CPD,
理由如下:∵AB=AC,
∴∠ABC=∠ACB,
∵∠APC=∠ABC+∠BAP,
∴∠APD+∠DPC=∠ABC+∠BAP,
又∵∠APD=∠B,
∴∠DPC=∠BAP,
∴△BAP∽△CPD;
(2)∵PD∥AB,
∴∠APD=∠BAP,
又∵∠APD=∠B,
∴∠BAP=∠B=∠C,
又∵∠B=∠B,
∴△ABC∽△PBA,
∴,
∴,
∴BP=.
23.解:(1)分别作EE1,FF1平行于BC且与AD交于E1、F1两点.
则==,==,
又BD=CD,
∴=∴==;
(2)设AF1=y,F1P=4x,PE1=5x,E1D=z,
则=,=,
解得y=36x,z=15x,
∴===.
24.解:(1)∵矩形ABCD中,∠BAD=90°,AB=3,AD=4,
∴==5,
∵AE=EF,∠A=∠EFB=90°,
∴∠EFD=90°,
∴∠EFD=∠BAD,
∵∠EDF=∠ADB,
∴△DEF∽△DBA,
∴,
设AE=EF=x,则DE=4﹣x,
∴
解得x=,
∴AE=;
(2)证明:∵F为BD的中点,∠A=∠BFE=90°,
∴BE=DE,
∴∠EBD=∠EDB,
∵MN∥BE,
∴∠NME=∠BEM,
又∵MN平分∠EMD,
∴∠NMD=∠NME,
∴∠NMD=∠BEM
∴△BEM∽△DMN,
∴,
∴,
∴DN?DE=DM?BM.
第1页(共1页)
重点题型专题练习(二)
一.选择题
1.已知=2,则的值是( )
A. B.﹣ C.3 D.﹣3
2.如图,已知AD∥BE∥CF,那么下列结论正确的是( )
A.= B.= C.= D.=
3.如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,点A,B,E在x轴上.若正方形ABCD的边长为2,则点F坐标为( )
A.(8,6) B.(9,6) C. D.(10,6)
4.如图,在△ABC中,DE∥AB,且,则的值为( )
A. B. C. D.
5.如图,下列条件中不能判定△ACD∽△ABC的是( )
A.∠ADC=∠ACB B. C.∠ACD=∠B D.AC2=AD?AB
6.若如图所示的两个四边形相似,则∠α的度数是( )
A.75° B.60° C.87° D.120°
7.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中第九卷《勾股》章,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑,东西七里,南北九里,各中开门,出东门一十五里有木,问:出南门几何步而见木?”
译文:“今有一座长方形小城,东西向城墙长7里,南北向城墙长9里,各城墙正中均开一城门.走出东门15里处有棵大树,问走出南门多少步恰好能望见这棵树?”(注:1里=300步)
你的计算结果是:出南门几何步而见木( )
A.300步 B.315 步 C.400 步 D.415步
8.如图,顽皮的小聪在小芳的作业本上用红笔画了个“×”(作业本中的横格线都平行,且相邻两条横格线间的距离都相等),A、B、C、D、O都在横格线上,且线段AD、BC交于点O.若线段AB=4cm,则线段CD长为( )
A.4cm B.5cm C.6cm D.8cm
9.如图,在?ABCD中,AB=10,AD=15,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,若BG=8,则△CEF的周长为( )
A.16 B.17 C.24 D.25
10.如图所示,以长为2的线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,
使PF=PD,以AF为边作正方形AMEF,点M在AD上,则AM的长为( )
A.﹣1 B. C.3﹣ D.6﹣2
11.如图,在?ABCD中,对角线AC与BD相交于点O,点E是BC的中点,AE与BD相交于点G,则的值为( )
A. B. C. D.
12.如图矩形ABCD中,E是CD延长线上一点,连结BE交AD于点F,连结CF,已知AB=1,BC=2,若△ABF与△CEF的面积相等,则DE的长为( )
A.1 B. C. D.
二.填空题
13.如果=,那么的值等于 .
14.如图,抛物线y=+2与x轴交于A、B两点(A在B左侧),与y轴交于点C,动直线EF(EF∥x轴)从点C出发,以每秒1个单位长度的速度沿y轴负方向平移,且分别交y轴,线段BC于E、F两点,动点P同时从点B出发,在线段OB上以每秒2个单位长度的速度向原点O运动.当出发 秒时,△BPF与△ABC相似.
15.如图,身高1.8米的小石从一盏路灯下B处向前走了8米到达点C处时,发现自己在地面上的影子CE长是2米,则路灯的高AB为 米.
16.如图,在△ACM中,△ABC、△BDE、△DFG是等边三角形,点E、G在△ACM的边CM上,设△ABC、△BDE、△DFG的面积分别为S1、S2、S3,若S1=8,S3=2,则S2= .
17.如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,点D是△ABC内一个动点,且满足∠DAB=∠DBC,当线段CD取最小值时,记∠BCD=α,线段AB上一动点E绕着点D顺时针旋转得到点F,且满足∠EDF=α,则AF的最小值 .
三.解答题
18.如图,在矩形ABCD中,AB=2,AD=4.点E,F分别在AD,BC上,点A与点C关于EF所在的直线对称,P是边DC上的一动点.
(1)连接AF,CE,求证:四边形AFCE是菱形;
(2)当△PEF的周长最小时,求的值.
19.以下各图均是由边长为1的小正方形组成的网格,图中的点A、B、C、D均在格点上.
(1)在图①中,PC:PB= .
(2)利用网格和无刻度的直尺作图,保留痕迹,不写作法.
①如图②,在AB上找一点P,使AP=3.
②如图③,在BD上找一点P,使△APB∽△CPD.
20.如图,在正方形ABCD中,在BC边上取中点E,连接DE,过点E做EF⊥ED交AB于点G、交AD延长线于点F.
(1)求证:△ECD∽△DEF;
(2)若CD=4,求AF的长.
21.如图,△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD,CE交于点F,连接DE.
(1)求证:△ABD∽△ACE;
(2)求证:△ADE∽△ABC;
(3)若BE=CE=,CD=1,求DF的长.
22.如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B.
(1)判定△ABP与△PCD是否相似,说明理由;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.
23.已知:△ABC中,D为BC的中点,E为AB上一点,且BE=AB.F为AC上一点,且CF=AC,EF交AD于P.
(1)求EP:PF的值.
(2)求AP:PD的值.
24.已知,矩形ABCD,点E是AD上一点,将矩形沿BE折叠,点A恰好落在BD上点F处.
(1)如图1,若AB=3,AD=4,求AE的长;
(2)如图2,若点F恰好是BD的中点,点M是BD上一点,过点M作MN∥BE交AD于点N,连接EM,若MN平分∠EMD,求证:DN?DE=DM?BM.
参考答案
一.选择题
1.解:∵=2,
∴b=2a,
∴==﹣.
故选:B.
2.解:∵AD∥BE∥CF,
∴,,
故A、D、C错误,B正确.
故选:B.
3.解:∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,
∴==,
∵BC=2,
∴EF=BE=6,
∵BC∥EF,
∴△OBC∽△OEF,
∴=,
解得:OB=3,
∴EO=9,
∴F点坐标为:(9,6),
故选:B.
4.解:∵=,
∴=,
∵DE∥AB,
∴==,
故选:A.
5.解:A、由∠ADC=∠ACB,∠A=∠A可得△ACD∽△ABC,此选项不符合题意;
B、由不能判定△ACD∽△ABC,此选项符合题意;
C、由∠ACD=∠B,∠A=∠A可得△ACD∽△ABC,此选项不符合题意;
D、由AC2=AD?AB,即=,且∠A=∠A可得△ACD∽△ABC,此选项不符合题意;
故选:B.
6.解:根据相似多边形的特点可知对应角相等,所以∠α=360°﹣60°﹣138°﹣75°=87°.故选C.
7.解:由题意得,AB=15里,AC=4.5里,CD=3.5里,
△ACB∽△DEC,
∴=,即=,
解得,DE=1.05里=315步,
∴走出南门315步恰好能望见这棵树,
故选:B.
8.解:如图,过点O作OE⊥AB于点E,OF⊥CD于点F,则OE、OF分别是△AOB、△DOC的高线,
∵练习本中的横格线都平行,
∴△AOB∽△DOC,
∴=,即=,
∴CD=6cm.
故选:C.
9.解:∵在?ABCD中,CD=AB=10,BC=AD=15,∠BAD的平分线交BC于点E,
∴AB∥DC,∠BAF=∠DAF,
∴∠BAF=∠F,
∴∠DAF=∠F,
∴DF=AD=15,
同理BE=AB=10,
∴CF=DF﹣CD=15﹣10=5;
∴在△ABG中,BG⊥AE,AB=10,BG=8,
在Rt△ABG中,AG===6,
∴AE=2AG=12,
∴△ABE的周长等于10+10+12=32,
∵四边形ABCD是平行四边形,
∴AB∥CF,
∴△CEF∽△BEA,相似比为5:10=1:2,
∴△CEF的周长为16.
故选:A.
10.解:在Rt△APD中,AP=1,AD=2,
由勾股定理知PD===,
∴AM=AF=PF﹣AP=PD﹣AP=﹣1.
故选:A.
11.解:∵点E是BC的中点,
∴BC=2BE,
∵四边形ABCD是平行四边形,
∴OB=OD,AD=BC=2BE,AD∥BC,
∴△BEG∽△DAG,
∴==,
∴DG=2BG,
∴BD=3BG,OD=OB=BG,
∴=;
故选:C.
12.解:设DE=x.
∵DF∥BC,
∴△EFD∽△EBC,
∴=,
∴=,
∴DF=,AF=2﹣=,
∵△ABF与△CEF的面积相等,
∴?AF?AB=?EC?DF,
∴×1=×(x+1),
∴解得x=或(舍弃),
故选:D.
二.填空题(共5小题)
13.解:∵=,
∴3x﹣3y=2x,
故x=3y
∴=3.
故答案为:3.
14.解:∵抛物线y=x+2与x轴交于A、B两点(A在B左侧),与y轴交于点C,
∴令y=0,得x+2=0,解得x=2或x=4,
∴A(2,0),B(4,0),
当x=0时,y=2,
∴C(0,2),
在Rt△BOC中,OC=2,OB=4,
∴BC===2,
∵EF∥OB,
∴,
∴,
∴BF=(2﹣t),
BP=2t(0<t≤2).
①当FP∥AC时,△BFP∽△BCA,
∴,
∴,
解得t=.
②当时,△BFP∽△BAC,
∴,
解得t=,
综上所述,满足条件的t的值为s或s.
故答案为:或.
15.解:由题意知,CE=2米,CD=1.8米,BC=8米,CD∥AB,
则BE=BC+CE=10米,
∵CD∥AB,
∴△ECD∽△EBA
∴=,即=,
解得AB=9(米),
即路灯的高AB为9米;
故答案为:9.
16.解:△ABC、△BDE、△DGF的边长分别是a、b、c,
∵△ABC、△BDE是等边三角形,
∴∠CBA=∠EBD=60°,
∴∠CBE=60°,
同理∠EDG=60°,
∴∠CBE=∠EDG,
∵△BDE、△DGF是等边三角形,
∴∠EBD=∠GDF=60°,
∴BE∥DG,
∴∠CEB=∠EGD,
∴△CBE∽△EDG,
∴a:b=b:c,
∴b2=ac,
∵S1:S3=(a:c)2=8:2=4:1,
∴a:c=2:1,
∵S1:S2=()2====,
∴S2=S1=4.
故答案是4.
17.解:∵AB⊥BC,AB=6、BC=4,
∴∠DBC+∠ABD=90°,
∵∠DAB=∠DBC,设∠DAB=∠DBC=β,
∴∠DAB+∠ABD=90°,
∴∠ADB=90°,
∴点D在以AB为直径的圆上,设圆心为O,半径为AB=3,则当O、D、C三点共线时CD最小,
∴OD=OB=OA=3,
∴OC==5,
将DA绕点D逆时针旋转α,得到DG,连接GE,
∴DG=DA,
∠GDA=∠EDF=α,
∴∠GDE=∠ADF,
∵DE=DF,
∴△GDE≌△ADF(SAS),
∴GE=AF,
∴当GE⊥AB时,GE最小,即AF最小,
过点D作DM⊥AB于M,过点G作GH⊥DM,交DM的延长线于点H,
∴DM∥BC,四边形GHME为矩形.
∴△OMD∽△OBC,GE=HM,
∴,
∴,
∴DM=,OM=,
∴AM=OM+OA=+3=,
∵∠DAB=∠DBC=β,OA=OD,
∴∠ODA=∠OAD=β,
∴∠BOC=∠ODA+∠OAD=2β.
∵在Rt△OBC中,∠OCB=90°﹣∠BOC,
∴α=90°﹣2β,
∵∠MAD+∠MDA=90°,
∴β+α+∠GDH=90°,
∴∠GDH=β=∠DAM,
∵∠DHG=∠AMD=90°,AD=DG,
∴△GDH≌△DAM(AAS).
∴DH=AM=,
∴HM=DH﹣DM=,即AF的最小值为.
故答案为:.
三.解答题(共7小题)
18.解:(1)证明:如图,连接AF,CE,AC交EF于点O
∵四边形ABCD是矩形
∴AB=CD,AD=BC,AD∥BC
∴∠AEO=∠CFO,∠EAO=∠FCO
∵点A与点C关于EF所在的直线对称
∴AO=CO,AC⊥EF
∵∠AEO=∠CFO,∠EAO=∠FCO,AO=CO
∴△AEO≌△CFO(AAS)
∴AE=CF,且AE∥CF
∴四边形AFCE是平行四边形,
又∵AC⊥EF
∴四边形AFCE是菱形;
(2)如图,作点F关于CD的对称点H,连接EH,交CD于点P,此时△PEF的周长最小
∵四边形AFCE是菱形
∴AF=CF=CE=AE
∵AF2=BF2+AB2
∴AF2=(4﹣AF)2+4
∴AF=
∵AD∥BC
∴△DEP∽△CHP
∴==.
答:当△PEF的周长最小时,的值为.
19.解:(1)图1中,
∵AB∥CD,
∴==,
故答案为1:3.
(2)
①如图2所示,点P即为所要找的点;
②如图3所示,作点A的对称点A′,
连接A′C,交BD于点P,
点P即为所要找的点,
∵AB∥CD,
∴△APB∽△CPD.
20.(1)证明:∵四边形ABCD是正方形,EF⊥ED,
∴∠FED=∠C=90°,BC∥AD,
∴∠CED=∠FDE,
∴△ECD∽△DEF;
(2)解:∵四边形ABCD是正方形,
∴∠C=90°,AD=BC=CD=4,
∵E为BC的中点,
∴CE=BC=2,
在Rt△DCE中,由勾股定理得:DE===2,
∵△ECD∽△DEF,
∴=,
∴=,
解得:DF=10,
∵AD=4,
∴AF=DF﹣AD=10﹣4=6.
21.(1)证明;∵BD⊥AC于点D,CE⊥AB于点E,
∴∠ADB=∠AEC=90°,
∵∠A=∠A,
∴△ADB∽△AEC.
(2)证明:∵△ADB∽△AEC,
∴=,
∴=,
∵∠A=∠A,
∴△ADE∽△ABC.
(3)解:过点E作EN⊥ED交BD于N,过点E作EM⊥DN于M.
在Rt△BEC中,∵BE=EC=,∠BEC=90°,
∴BC=BE=,∠BCF=45°,
∵∠BDC=90°,
∴BD===3,
∵∠EFB=∠DFC,∠BEF=∠CDF=90°,
∴△BFE∽△CFD,
∴=,
∴=,
∵∠EFD=∠BFC,
∴△EFD∽△BFC,
∴∠EDF=∠BCF=45°,
∵∠NED=90°,
∴∠END=∠EDN=45°,
∴EN=ED,
∵∠BEC=∠NED=90°,
∴∠BEN=∠CED,
∵BE=CE,
∴△BEN≌△CED(SAS),
∴BN=CD=1,DN=BD﹣BN=2,
∵EN=ED,EM⊥DN,
∴MN=DM=1,
∴EM=MN=MD=1,
∵∠EMF=∠CDF=90°,∠EFM=∠CFD,EM=CD,
∴△EMF≌△CDF(AAS),
∴MF=DF,
∴DF=.
22.解:(1)△BAP∽△CPD,
理由如下:∵AB=AC,
∴∠ABC=∠ACB,
∵∠APC=∠ABC+∠BAP,
∴∠APD+∠DPC=∠ABC+∠BAP,
又∵∠APD=∠B,
∴∠DPC=∠BAP,
∴△BAP∽△CPD;
(2)∵PD∥AB,
∴∠APD=∠BAP,
又∵∠APD=∠B,
∴∠BAP=∠B=∠C,
又∵∠B=∠B,
∴△ABC∽△PBA,
∴,
∴,
∴BP=.
23.解:(1)分别作EE1,FF1平行于BC且与AD交于E1、F1两点.
则==,==,
又BD=CD,
∴=∴==;
(2)设AF1=y,F1P=4x,PE1=5x,E1D=z,
则=,=,
解得y=36x,z=15x,
∴===.
24.解:(1)∵矩形ABCD中,∠BAD=90°,AB=3,AD=4,
∴==5,
∵AE=EF,∠A=∠EFB=90°,
∴∠EFD=90°,
∴∠EFD=∠BAD,
∵∠EDF=∠ADB,
∴△DEF∽△DBA,
∴,
设AE=EF=x,则DE=4﹣x,
∴
解得x=,
∴AE=;
(2)证明:∵F为BD的中点,∠A=∠BFE=90°,
∴BE=DE,
∴∠EBD=∠EDB,
∵MN∥BE,
∴∠NME=∠BEM,
又∵MN平分∠EMD,
∴∠NMD=∠NME,
∴∠NMD=∠BEM
∴△BEM∽△DMN,
∴,
∴,
∴DN?DE=DM?BM.
第1页(共1页)
