冀教版数学八年级上册13.4《一元一次不等式(组)》课件
文档属性
| 名称 | 冀教版数学八年级上册13.4《一元一次不等式(组)》课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 641.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-27 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
一元一次不等式(组)
回顾与反思
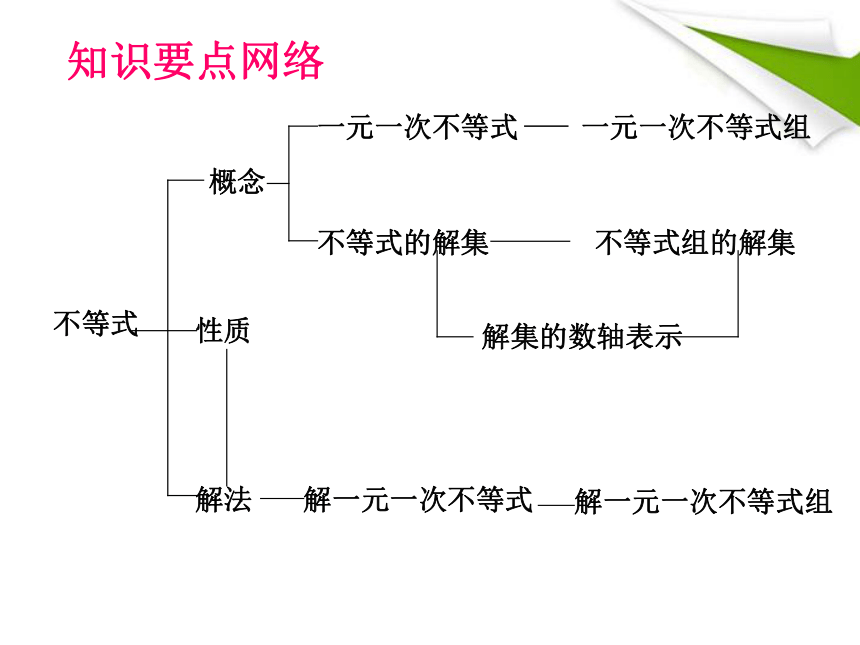
知识要点网络
不等式
概念
性质
解法
一元一次不等式
不等式的解集
一元一次不等式组
不等式组的解集
解一元一次不等式
解一元一次不等式组
解集的数轴表示
你能行
1、判断下列各式哪些是不等式?哪些不是?
① 3>2;② x+3<5;③ 4>6;④ 2x+1;
⑤ 5x+2=7x ⑥ a≠3⑦ 2x+3y≤9
属于不等式的有 ;
不属于不等式的有 。
①②③⑥⑦
④⑤
2、用不等式表示下列数量关系:
(1)a的一半与-3的和小于或等于1
(2)x的3倍与y的5倍的和不大于3.
3x+5y≤3
不等式的概念:
用不等号表示不等关系的式子,叫做不等式
一元一次不等式:
含有一个未知数且未知数的次数都是1次的不等式叫做一元一次不等式。
如:低于、超过、最高、最低、最多、最少、至少、不高于、不低于、不大于、不小于、
列不等式时,要弄清不等关系,抓关键词。
以及用符号如何表示。
你能行
1.若-m>5,则m -5.
2.若a>b, 则2a 2b;
3.不等式3x-2<-1解集是 .
4.如果a>-1,那么a-b -1-b.
>
>
<
1/3
X<
5.不等式 的解集为( )
6.不等式 正整数解的个数是( )
A. 2
B. 3
C.4
D. 5
C
不等式的基本性质:
性质1 不等式两边都加上(或减去)同一个数或同一个整式,不等号的方向不变。
性质2 不等式两边同乘以(或除以)同一个正数,不等号的方向不变。
性质3 不等式两边同乘以(或除以)同一个负数,不等号的方向改变。
1、不等式的解:使不等式成立的未知数的值叫做不等式的解。
2、不等式的解集:一般地说,一个含有未知数的不等式的所有的解,组成这个等式的解的集合,简称这个不等式的解集。
二者的区别:不等式的解是指满足这个不等式的未知数的某个值,而不等式的解集,是指满足这个不等式的未知数的所有的值,不等式的所有解组成了解集.
去分母
去括号
移项
合并同类项
未知数的系数化为1
注意用不等式性质3,即不等式两边乘或除以一个负数时,改变不等号的方向。
用数轴表示下列不等式的解集:
① x>-1; ② x≤-1 ;③ x<-1; ④ x≥-1 .
(1)用数轴表示不等式的解集分三步进行:第一步:画出数轴;第2步,定界点;第3步:定方向.
(2)用数轴表示不等式的解集,还应记住下面规律:
大于向右画,小于向左画,有等(≥,≤)画实心,无等号(>、<、≠)画空心圆.
①.
解:如图
③.
④.
解:解不等式① .得
解不等式② .得
在同一条数轴上表示不等式① ②的解集,如图:
因此,原不等式组的解集为:
x<6
解不等式组:
2x-1> -x ①
②
2.一元一次不等式组中各个不等式的解集的
公共部分, 叫做这个一元一次不等式组的解集.
求不等式组解集的过程,叫做解不等式组.
3.解一元一次不等式组的步骤:
①求出这个不等式组中各个不等式的解集.
②利用数轴求出这些不等式解集的公共部分.
③表示这个不等式组的解集.
1.一般地,关于同一未知数的几个一元一次不等式
合在一起,就组成一个
一元一次不等式组
不等式组的解集
不等式组
无 解
数轴表示
解集
解不等式组:
1.
2.
的解不小于-3。
x=2m+2
若 ,求当 时,m的取值范围。
1. 设“A、B、C、D”表示四种不同质量的物体,在天平秤上的情况如图所示,请你用“<”号将这四种物体的质量mA、mB、mC、mD从小到大排列:_____________________________。
课堂检测:
2.解下列不等式或不等式组
(1) ( 2.) 2x-3<1
x+2<0
{
你掌握了哪些知识?
作业:总复习题
例6. 东风商场文具部的某种毛笔每枝售价25元,书法练习本每本售价5元,该商场为促销制定了两种优惠办法。
甲:买一枝毛笔就赠送一本练习本;
乙:按购买金额打九折付款。
某校欲为书法兴趣小组购买这种毛笔10枝,书法练习本x(x≥10)本。
(1)写出每种优惠办法实际付款金额
y甲(元),y乙(元)与x(本)之间的函数关系式;
(2)购买同样多的书法练习本时,按哪种优惠办法付款更省钱;
由y甲=y乙,得5x+200=4.5x+225,解之得x=50。
由y甲>y乙,得5x+200>4.5x+22.5,解之得x>50;
由y甲所以,当购买50本书法练习本时,
两种优惠办法的实际付款金额相等,可以任选一种优惠
当购买书法练习本的本数多于50本书,选择乙优惠办法付款更省钱;
当购买书法练习本的本数不少于10本且多于50本时,
选择甲优惠办法付款更省钱。
甲、乙两旅行社假期搞组团促销活动,甲:“若领队买一张全票,其余可半价优惠”。乙“包括领队在内,一律按全票价的六折优惠”。已知全票价为120元,你认为选择哪家旅行社更优惠?
(1)由 ,得
解之得x<4
(2)由 ,得
解之得x=4
(3)由 ,得
解之得x>4
某工厂有甲种原料360kg,乙种原料290kg,计划用这两种原料生产A、B两种产品共50件。已知生产一件A种产品,需用甲种原料9kg,乙种原料3kg,可获利润700元:生产一件B种产品,需用甲种原料4kg,乙种原料10kg,可获利润1200元。
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请你设计出来。
(2)设生产A、B两种产品获总利润W(元),采用哪种生产方案获总利润最大?最大利润为多少?
故第一种方案为:生产A产品30件,B产品20件;
第二种方案为:生产A产品31件,B产品19件;
第三种方案为:生产A产品32件,B产品18件。
一元一次不等式(组)
回顾与反思
知识要点网络
不等式
概念
性质
解法
一元一次不等式
不等式的解集
一元一次不等式组
不等式组的解集
解一元一次不等式
解一元一次不等式组
解集的数轴表示
你能行
1、判断下列各式哪些是不等式?哪些不是?
① 3>2;② x+3<5;③ 4>6;④ 2x+1;
⑤ 5x+2=7x ⑥ a≠3⑦ 2x+3y≤9
属于不等式的有 ;
不属于不等式的有 。
①②③⑥⑦
④⑤
2、用不等式表示下列数量关系:
(1)a的一半与-3的和小于或等于1
(2)x的3倍与y的5倍的和不大于3.
3x+5y≤3
不等式的概念:
用不等号表示不等关系的式子,叫做不等式
一元一次不等式:
含有一个未知数且未知数的次数都是1次的不等式叫做一元一次不等式。
如:低于、超过、最高、最低、最多、最少、至少、不高于、不低于、不大于、不小于、
列不等式时,要弄清不等关系,抓关键词。
以及用符号如何表示。
你能行
1.若-m>5,则m -5.
2.若a>b, 则2a 2b;
3.不等式3x-2<-1解集是 .
4.如果a>-1,那么a-b -1-b.
>
>
<
1/3
X<
5.不等式 的解集为( )
6.不等式 正整数解的个数是( )
A. 2
B. 3
C.4
D. 5
C
不等式的基本性质:
性质1 不等式两边都加上(或减去)同一个数或同一个整式,不等号的方向不变。
性质2 不等式两边同乘以(或除以)同一个正数,不等号的方向不变。
性质3 不等式两边同乘以(或除以)同一个负数,不等号的方向改变。
1、不等式的解:使不等式成立的未知数的值叫做不等式的解。
2、不等式的解集:一般地说,一个含有未知数的不等式的所有的解,组成这个等式的解的集合,简称这个不等式的解集。
二者的区别:不等式的解是指满足这个不等式的未知数的某个值,而不等式的解集,是指满足这个不等式的未知数的所有的值,不等式的所有解组成了解集.
去分母
去括号
移项
合并同类项
未知数的系数化为1
注意用不等式性质3,即不等式两边乘或除以一个负数时,改变不等号的方向。
用数轴表示下列不等式的解集:
① x>-1; ② x≤-1 ;③ x<-1; ④ x≥-1 .
(1)用数轴表示不等式的解集分三步进行:第一步:画出数轴;第2步,定界点;第3步:定方向.
(2)用数轴表示不等式的解集,还应记住下面规律:
大于向右画,小于向左画,有等(≥,≤)画实心,无等号(>、<、≠)画空心圆.
①.
解:如图
③.
④.
解:解不等式① .得
解不等式② .得
在同一条数轴上表示不等式① ②的解集,如图:
因此,原不等式组的解集为:
x<6
解不等式组:
2x-1> -x ①
②
2.一元一次不等式组中各个不等式的解集的
公共部分, 叫做这个一元一次不等式组的解集.
求不等式组解集的过程,叫做解不等式组.
3.解一元一次不等式组的步骤:
①求出这个不等式组中各个不等式的解集.
②利用数轴求出这些不等式解集的公共部分.
③表示这个不等式组的解集.
1.一般地,关于同一未知数的几个一元一次不等式
合在一起,就组成一个
一元一次不等式组
不等式组的解集
不等式组
无 解
数轴表示
解集
解不等式组:
1.
2.
的解不小于-3。
x=2m+2
若 ,求当 时,m的取值范围。
1. 设“A、B、C、D”表示四种不同质量的物体,在天平秤上的情况如图所示,请你用“<”号将这四种物体的质量mA、mB、mC、mD从小到大排列:_____________________________。
课堂检测:
2.解下列不等式或不等式组
(1) ( 2.) 2x-3<1
x+2<0
{
你掌握了哪些知识?
作业:总复习题
例6. 东风商场文具部的某种毛笔每枝售价25元,书法练习本每本售价5元,该商场为促销制定了两种优惠办法。
甲:买一枝毛笔就赠送一本练习本;
乙:按购买金额打九折付款。
某校欲为书法兴趣小组购买这种毛笔10枝,书法练习本x(x≥10)本。
(1)写出每种优惠办法实际付款金额
y甲(元),y乙(元)与x(本)之间的函数关系式;
(2)购买同样多的书法练习本时,按哪种优惠办法付款更省钱;
由y甲=y乙,得5x+200=4.5x+225,解之得x=50。
由y甲>y乙,得5x+200>4.5x+22.5,解之得x>50;
由y甲
两种优惠办法的实际付款金额相等,可以任选一种优惠
当购买书法练习本的本数多于50本书,选择乙优惠办法付款更省钱;
当购买书法练习本的本数不少于10本且多于50本时,
选择甲优惠办法付款更省钱。
甲、乙两旅行社假期搞组团促销活动,甲:“若领队买一张全票,其余可半价优惠”。乙“包括领队在内,一律按全票价的六折优惠”。已知全票价为120元,你认为选择哪家旅行社更优惠?
(1)由 ,得
解之得x<4
(2)由 ,得
解之得x=4
(3)由 ,得
解之得x>4
某工厂有甲种原料360kg,乙种原料290kg,计划用这两种原料生产A、B两种产品共50件。已知生产一件A种产品,需用甲种原料9kg,乙种原料3kg,可获利润700元:生产一件B种产品,需用甲种原料4kg,乙种原料10kg,可获利润1200元。
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请你设计出来。
(2)设生产A、B两种产品获总利润W(元),采用哪种生产方案获总利润最大?最大利润为多少?
故第一种方案为:生产A产品30件,B产品20件;
第二种方案为:生产A产品31件,B产品19件;
第三种方案为:生产A产品32件,B产品18件。
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
