2020-2021学年八年级数学人教版下册课件 17.1 勾股定理的应用(24张)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册课件 17.1 勾股定理的应用(24张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 281.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-27 00:28:59 | ||
图片预览







文档简介
八年级上册(RJ)
17.1勾股定理的应用
学习目标1
(1)能用勾股定理证明直角三角形全等的“斜边、直角边”判定定理;
(2)能应用勾股定理在数轴上画出表示无理数的点.
(3)体会勾股定理在数学中的地位和作用.
自学释疑、拓展提升
知识点一:利用勾股定理证明“HL”
自学问题:对几何知识的逻辑性和证明的必要性认 识不够深入.
八年级上册中曾经通过画图得到结论:斜边和一条直角边对应相等的两个直角三角形全等.
学习勾股定理后,能证明这一结论吗?
自学释疑、拓展提升
知识点一:利用勾股定理证明“HL”
已知:如图,在Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90°,
AB=A'B',AC=A'C'.求证:△ABC≌△A'B'C'.
问1:要证明这两个直角三角形三角形全等,有什么已知条件?还需什么条件?
问2:能通过现有条件证明BC=B'C' 吗?用什么方法?
自学释疑、拓展提升
知识点一:利用勾股定理证明“HL”
已知:如图,在Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90°,
AB=A'B',AC=A'C'.求证:△ABC≌△A'B'C'.
证明:∵在Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90°.根据勾股定理,得BC= ,
B'C'= .又∵AB=A'B',AC=A'C',∴BC=B'C'.
∴△ABC≌△A'B'C'(SSS).
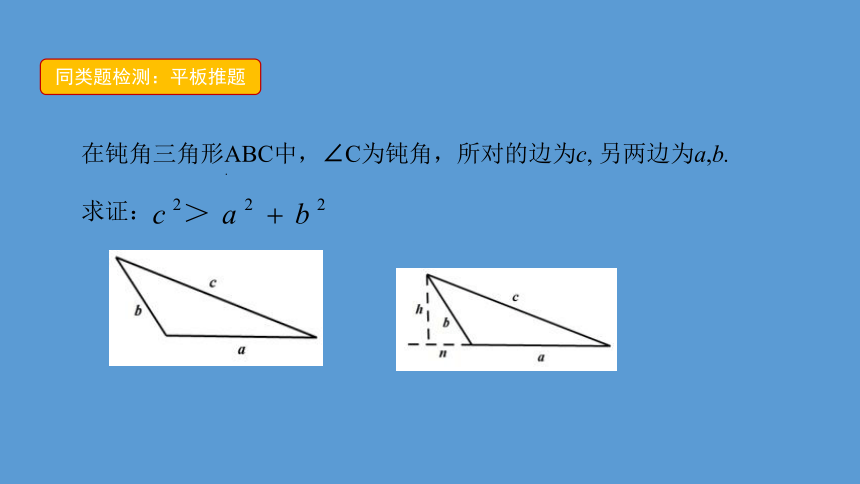
同类题检测:平板推题
在钝角三角形ABC中,∠C为钝角,所对的边为c, 另两边为a,b.
求证:
.
自学释疑、拓展提升
知识点二:画图探究——在数轴上画出无理数点
自学问题:能画出长度为无理数的线段,理解数轴上的点所表示的数,既有有理数,又有无理数.在探究和操作过程中学习构造法,体会数形结合的思想.
学生典型问题展示:《勾股定理的应用课前自测》中第1-3题的正确率以及做错的学生的错题选项;教材中27页练习1做错学生的错题内容.
自学释疑、拓展提升
知识点二:画图探究——在数轴上画出无理数点
问题解决:
知道数轴上的点有的表示有理数,有的表示无理数,在七年级知道可以将 ,π表示在数轴上,是否所有的无理数都能在数轴上画出呢?能表示 的点吗?
画法如下:如图,在数轴上找出表示3的点A,则OA=3,过点A作直线l垂直于OA,在l上取点B,使AB=1,连接OB,则OB= ,以原点O为圆心,以OB为半径作弧,弧与数轴的交点C即为表示的点.
自学释疑、拓展提升
知识点二:画图探究——在数轴上画出无理数点
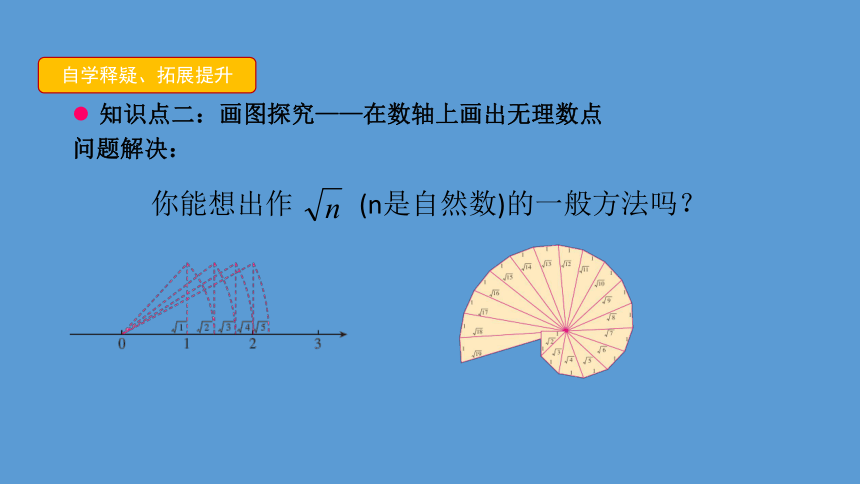
问题解决:
你能想出作 (n是自然数)的一般方法吗?
自学释疑、拓展提升
知识点三:勾股定理的综合应用
自学问题:在复杂图形中不能综合运用勾股定理.
学生典型问题展示:《勾股定理的应用课前自测》中第4题的正确率,以及做错的学生的错题选项;教材中27页练习2做错学生的错题内容.
同类题检测:平板推题
1.如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴于点M,则点M表示的数为( )
2.以下是在数轴上表示出 的点的作图过程,请你把它补充完整. (1)在数轴上找到点A,使OA=______; (2)作直线l____OA,在l上取一点B,使AB=_____; (3)以原点O为圆心,以______为半径作弧,弧与数轴交于C点,则点C即为表示______的点.
自学释疑、拓展提升
知识点三:勾股定理的综合应用
问题解决:
例 如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,求证:AD2+DB2=DE2.
证明:∵∠ACB=∠ECD,∴ ∠ACD+∠BCD=∠ACD+∠ACE.即 ∠BCD=∠ACE.∵ BC=AC,DC=EC, ∴ △ACE≌△BCD.∴ ∠B=∠CAE=45°,AE=DB.∴ ∠DAE=∠CAE+∠BAC=45°+45°=90°.∴ AD2+AE2=DE2.∴ AD2+DB2=DE2.
同类题检测:平板推题
已知:如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,AD=1,CD= ,求线段AB的长.
课堂小结
(1)勾股定理最根本作用是什么,本节课学习了勾股定理哪 几方面的应用?
(2)能说说勾股定理求线段长的基本思路吗?
(3)本节课体现出哪些数学思想方法?
学习目标2
1.能运用勾股定理求线段长度,并解决一些简单的实际问题;
2.在利用勾股定理解决实际生活问题的过程中,能从实际问题中抽象出直角三角形这一几何模型,利用勾股定理建立已知边与未知边长度之间的联系,并进一步求出未知边长.
自学释疑、拓展提升
知识点一:利用勾股定理建立模型,解决问题
自学问题:建立数学模型,利用勾股定理解决问题.
学生典型问题展示:《勾股定理应用课前自测》中第1、2题的正确率,以及做错 的学生的错题选项;教材中26页练习1做错学生的错题内容.
自学释疑、拓展提升
知识点一:利用勾股定理建立模型,解决问题
问题解决:
上一节学习勾股定理,请叙述勾股定理?
如果直角三角形两直角边长分别为a,b,斜边长为c,
那么a2+b2=c2.
勾股定理能解决什么问题?
自学释疑、拓展提升
知识点一:利用勾股定理建立模型,解决问题
例1 我国古代有很多利用勾股定理解决的名题,《九章算术》中就有这样一个问题(书本P29第10题): 今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐,问水深、葭长各几何? 翻译成现代文如下:有一个水池,水面是一个边长为10尺的正方形,水池正中央长着一株芦苇,芦苇露出水面1尺.若将芦苇拉到岸边,刚好能达到水池岸与水面的交接线的中点上.水深与芦苇的长各有多少尺?
自学释疑、拓展提升
知识点一:利用勾股定理建立模型,解决问题
问1:能否将这个实际问题转化为数学问题,建立几何模型,画出图形?
问2:题目中哪些是已知量,哪些是待求量?
同类题检测:平板推题
如图,将一根长24 cm的筷子置于底面直径为5 cm,高为12 cm的圆柱形水杯中,设筷子露在杯子外面的长是h cm,则h的取值范围是______________.
自学释疑、拓展提升
知识点二:勾股定理解决三角形问题
自学问题:灵活应用勾股定理解决复杂的三角形问题.
学生典型问题展示:《勾股定理课前自测》中第3、4题的正确率以及做错的学生的错题选项;教材中26页练习2做错学生的错题内容.
自学释疑、拓展提升
知识点二:勾股定理解决三角形问题
问题解决:
例2.如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE=3m,求点B到地面的垂直距离BC.
同类题检测:平板推题
已知:如图,在Rt△ABC中,∠C=90°,AC= ,点D为BC边上一点,且BD=2AD,∠ADC=60°,求△ABC的周长.(结果保留根号)
课堂总结
1.利用勾股定理解决实际问题有哪些基本步骤?
2.解决实际问题的难点在哪里?有什么好的突破办法?利 用勾股定理解决实际问题的注意点是什么?请大家交流.
3.本节课体现了哪些数学思想方法,都在什么情况下运用?
17.1勾股定理的应用
学习目标1
(1)能用勾股定理证明直角三角形全等的“斜边、直角边”判定定理;
(2)能应用勾股定理在数轴上画出表示无理数的点.
(3)体会勾股定理在数学中的地位和作用.
自学释疑、拓展提升
知识点一:利用勾股定理证明“HL”
自学问题:对几何知识的逻辑性和证明的必要性认 识不够深入.
八年级上册中曾经通过画图得到结论:斜边和一条直角边对应相等的两个直角三角形全等.
学习勾股定理后,能证明这一结论吗?
自学释疑、拓展提升
知识点一:利用勾股定理证明“HL”
已知:如图,在Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90°,
AB=A'B',AC=A'C'.求证:△ABC≌△A'B'C'.
问1:要证明这两个直角三角形三角形全等,有什么已知条件?还需什么条件?
问2:能通过现有条件证明BC=B'C' 吗?用什么方法?
自学释疑、拓展提升
知识点一:利用勾股定理证明“HL”
已知:如图,在Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90°,
AB=A'B',AC=A'C'.求证:△ABC≌△A'B'C'.
证明:∵在Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90°.根据勾股定理,得BC= ,
B'C'= .又∵AB=A'B',AC=A'C',∴BC=B'C'.
∴△ABC≌△A'B'C'(SSS).
同类题检测:平板推题
在钝角三角形ABC中,∠C为钝角,所对的边为c, 另两边为a,b.
求证:
.
自学释疑、拓展提升
知识点二:画图探究——在数轴上画出无理数点
自学问题:能画出长度为无理数的线段,理解数轴上的点所表示的数,既有有理数,又有无理数.在探究和操作过程中学习构造法,体会数形结合的思想.
学生典型问题展示:《勾股定理的应用课前自测》中第1-3题的正确率以及做错的学生的错题选项;教材中27页练习1做错学生的错题内容.
自学释疑、拓展提升
知识点二:画图探究——在数轴上画出无理数点
问题解决:
知道数轴上的点有的表示有理数,有的表示无理数,在七年级知道可以将 ,π表示在数轴上,是否所有的无理数都能在数轴上画出呢?能表示 的点吗?
画法如下:如图,在数轴上找出表示3的点A,则OA=3,过点A作直线l垂直于OA,在l上取点B,使AB=1,连接OB,则OB= ,以原点O为圆心,以OB为半径作弧,弧与数轴的交点C即为表示的点.
自学释疑、拓展提升
知识点二:画图探究——在数轴上画出无理数点
问题解决:
你能想出作 (n是自然数)的一般方法吗?
自学释疑、拓展提升
知识点三:勾股定理的综合应用
自学问题:在复杂图形中不能综合运用勾股定理.
学生典型问题展示:《勾股定理的应用课前自测》中第4题的正确率,以及做错的学生的错题选项;教材中27页练习2做错学生的错题内容.
同类题检测:平板推题
1.如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴于点M,则点M表示的数为( )
2.以下是在数轴上表示出 的点的作图过程,请你把它补充完整. (1)在数轴上找到点A,使OA=______; (2)作直线l____OA,在l上取一点B,使AB=_____; (3)以原点O为圆心,以______为半径作弧,弧与数轴交于C点,则点C即为表示______的点.
自学释疑、拓展提升
知识点三:勾股定理的综合应用
问题解决:
例 如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,求证:AD2+DB2=DE2.
证明:∵∠ACB=∠ECD,∴ ∠ACD+∠BCD=∠ACD+∠ACE.即 ∠BCD=∠ACE.∵ BC=AC,DC=EC, ∴ △ACE≌△BCD.∴ ∠B=∠CAE=45°,AE=DB.∴ ∠DAE=∠CAE+∠BAC=45°+45°=90°.∴ AD2+AE2=DE2.∴ AD2+DB2=DE2.
同类题检测:平板推题
已知:如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,AD=1,CD= ,求线段AB的长.
课堂小结
(1)勾股定理最根本作用是什么,本节课学习了勾股定理哪 几方面的应用?
(2)能说说勾股定理求线段长的基本思路吗?
(3)本节课体现出哪些数学思想方法?
学习目标2
1.能运用勾股定理求线段长度,并解决一些简单的实际问题;
2.在利用勾股定理解决实际生活问题的过程中,能从实际问题中抽象出直角三角形这一几何模型,利用勾股定理建立已知边与未知边长度之间的联系,并进一步求出未知边长.
自学释疑、拓展提升
知识点一:利用勾股定理建立模型,解决问题
自学问题:建立数学模型,利用勾股定理解决问题.
学生典型问题展示:《勾股定理应用课前自测》中第1、2题的正确率,以及做错 的学生的错题选项;教材中26页练习1做错学生的错题内容.
自学释疑、拓展提升
知识点一:利用勾股定理建立模型,解决问题
问题解决:
上一节学习勾股定理,请叙述勾股定理?
如果直角三角形两直角边长分别为a,b,斜边长为c,
那么a2+b2=c2.
勾股定理能解决什么问题?
自学释疑、拓展提升
知识点一:利用勾股定理建立模型,解决问题
例1 我国古代有很多利用勾股定理解决的名题,《九章算术》中就有这样一个问题(书本P29第10题): 今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐,问水深、葭长各几何? 翻译成现代文如下:有一个水池,水面是一个边长为10尺的正方形,水池正中央长着一株芦苇,芦苇露出水面1尺.若将芦苇拉到岸边,刚好能达到水池岸与水面的交接线的中点上.水深与芦苇的长各有多少尺?
自学释疑、拓展提升
知识点一:利用勾股定理建立模型,解决问题
问1:能否将这个实际问题转化为数学问题,建立几何模型,画出图形?
问2:题目中哪些是已知量,哪些是待求量?
同类题检测:平板推题
如图,将一根长24 cm的筷子置于底面直径为5 cm,高为12 cm的圆柱形水杯中,设筷子露在杯子外面的长是h cm,则h的取值范围是______________.
自学释疑、拓展提升
知识点二:勾股定理解决三角形问题
自学问题:灵活应用勾股定理解决复杂的三角形问题.
学生典型问题展示:《勾股定理课前自测》中第3、4题的正确率以及做错的学生的错题选项;教材中26页练习2做错学生的错题内容.
自学释疑、拓展提升
知识点二:勾股定理解决三角形问题
问题解决:
例2.如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE=3m,求点B到地面的垂直距离BC.
同类题检测:平板推题
已知:如图,在Rt△ABC中,∠C=90°,AC= ,点D为BC边上一点,且BD=2AD,∠ADC=60°,求△ABC的周长.(结果保留根号)
课堂总结
1.利用勾股定理解决实际问题有哪些基本步骤?
2.解决实际问题的难点在哪里?有什么好的突破办法?利 用勾股定理解决实际问题的注意点是什么?请大家交流.
3.本节课体现了哪些数学思想方法,都在什么情况下运用?
