华东师大版九年级数学下册26.2.3求二次函数的表达式课件(共25张PPT)
文档属性
| 名称 | 华东师大版九年级数学下册26.2.3求二次函数的表达式课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-27 00:00:00 | ||
图片预览








文档简介
26.2 二次函数的图象与性质
3. 求二次函数的表达式
教学目标
教学重点与难点
重点:用待定系数法求二次函数的表达式.
难点:根据题目的已知条件,灵活选择合适的二次函数表达式.
1.掌握用待定系数法列方程组求二次函数解析式
的方法.
2.由已知条件的特点,灵活选择二次函数的两种形式,合理地设出函数解析式,可使计算过程更简便.
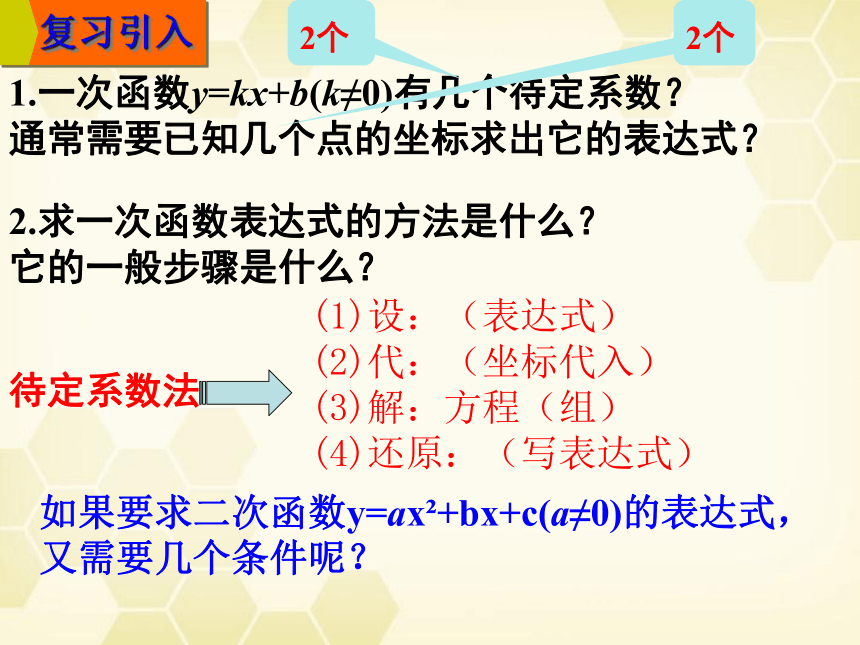
1.一次函数y=kx+b(k≠0)有几个待定系数?
通常需要已知几个点的坐标求出它的表达式?
2.求一次函数表达式的方法是什么?
它的一般步骤是什么?
2个
2个
待定系数法
(1)设:(表达式)
(2)代:(坐标代入)
(3)解:方程(组)
(4)还原:(写表达式)
复习引入
如果要求二次函数y=ax?+bx+c(a≠0)的表达式,
又需要几个条件呢?
例1 已知二次函数y=ax2 + c的图象经过点(2,3)
和(-1,-3),求这个二次函数的表达式.
解:∵该图象经过点(2,3)和(-1,-3),
3=4a+c,
-3=a+c,
∴所求二次函数表达式为 y=2x2-5.
∴{
a =2,
c =-5.
解得:
{
关于y轴对称
一.特殊条件的二次函数的表达式
学习新知
已知二次函数y=ax2 + bx的图象经过点(-2, 8)
和(-1,5),求这个二次函数的表达式.
解:∵该图象经过点(-2,8)和(-1,5) ,
图象经过原点
8=4a-2b,
5=a-b,
∴{
解得: a=-1,b=-6.
∴ 这个二次函数的表达式y=-x2-6x.
随堂练习
例2 已知二次函数的顶点是(-2, 1),且函数图象过点(1,-8),求这个二次函数的表达式.
解:设这个二次函数的表达式是y=a(x-h)2+k(a≠0),
∴ y=a(x+2)2+1,
∴ a(1+2)2+1=-8,
解得: a =-1.
∴所求二次函数的表达式是y=-(x+2)2+1或y=-x2-4x-3.
二.顶点法求二次函数的表达式
∵ 这个二次函数的顶点是(-2, 1),
∵ 函数图象过点(1, -8),
学习新知
顶点法求二次函数的表达式的步骤
①设函数表达式是y=a(x-h)2+k (a≠0);
方法总结
②先代入顶点坐标,得到关于a的一元一次方程;
③将另一点的坐标代入原方程求出a值;
④a用数值换掉,写出函数表达式.
(函数表达式的结果可以用顶点式或一般式表示)
例3 一个二次函数的图象经点 (0, 1),它的顶点坐标为(8,9),
求这个二次函数的表达式.
例题精析
解: ∵这个二次函数的图象的顶点坐标为(8,9),
∴ 设函数的表达式为y=a(x-8)2+9(a≠0).
又∵ 函数的图象经过点(0 ,1),
∴ 0=a(0-8)2+9.
解得:a= .
∴所求的二次函数的表达式是
1.抛物线的顶点在原点,且抛物线经过点(2,8),
求它的表达式.
随堂练习
解:∵抛物线的顶点在原点,
∴ 设它的表达式为y=ax2(a≠0).
∵ 抛物线经过点(2,8),
∴ 8=a×22,
∴ a=2.
∴ 所求抛物线的表达式为y=2x2.
2.抛物线的顶点坐标为(-1,-2),且抛物线经过
点(1,10),求该抛物线的表达式.
解: ∵抛物线的顶点坐标为(-1,-2),
∴ 设该抛物线的表达式为y=a(x+1)2-2(a≠0).
∵ 抛物线经过点(1,10),
∴ 10=a(1+1)2-2.
解得:a=3.
∴ 该抛物线的表达式为y=3(x+1)2-2.
即 y=3x2+6x+1.
学习新知
三.一般式法求二次函数的表达式
例4 一个二次函数的图象经过(0,1)、(2,4)、(3,10)三点,求这个二次函数的表达式.
解:设所求二次函数的表达式为y=ax2+bx+c,
∵ 函数的图象经过(0,1)、(2,4)、(3,10)三点,
解得:a= ,b= ,c= .
1
∴ 所求二次函数的表达式为
④把待定系数a,b,c用数字换掉,写出函数的表达式.
一般式法求二次函数的表达式的步骤
方法总结
①设函数的表达式为y=ax2+bx+c (a≠0) ;
②把已知点的坐标代入所设的表达式,得到一个
三元一次方程组;
③解方程组得到a,b,c的值;
随堂练习
1.已知抛物线y=ax2+bx+c经过三点:(-1,-1),(1,1),
(0,-2),求这条抛物线所对应的二次函数的表达式.
解:设所求二次函数的表达式为y=ax2+bx+c,
依题意得:
解得:a= ,b= ,c= .
-2
2
1
∴ 所求二次函数的表达式为y=2x2+x-2.
2.已知二次函数的图象经过(0, 3), (-2,-5), (1, 4),
求这个二次函数的表达式.
随堂练习
解:设所求二次函数的表达式为y=ax2+bx+c,
依题意得:
解得:a= ,b= ,c= .
3
-1
2
∴ 所求二次函数的表达式为y=-x2+2x+3.
交点法求二次函数的表达式的步骤
其步骤是:
①设函数的表达式是y=a(x-x1)(x-x2) (其中x1、x2为抛物线与x轴交点的横坐标;
②先把两交点的横坐标x1,x2代入到表达式中,得到关于a的一元一次方程;
③将已知的另一个条件代入方程求出a的值;
④a用数值换掉,写出函数表达式.
学习新知
知道抛物线与x轴的交点,求抛物线的表达式
的方法叫做交点法.
例题精析
例5 已知抛物线与x轴交于点A(-3,0)、B(5,0),
且与y轴交于点C(0, -15),求抛物线的解析式.
解:设所求抛物线的解析式是y=a(x+3)(x-5),
把点(0, -3)代入上式得:
a(0+3)(0-5)=-15,
解得:a= ,
1
∴ 所求抛物线的表达式为y=(x+3)(x-5),
即 y=x2-2x-15.
已知抛物线与x轴相交于点A(-1, 0),B(1, 0),且过点M(0,1),求此函数的表达式.
解:∵点A(-1,0),B(1,0)是图象与x轴的交点,
∴ 设二次函数的表达式为y=a(x+1)(x-1).
又∵抛物线过点M(0,1),
∴1=a(0+1)(0-1),
解得:a=-1,
∴所求抛物线的表达式为y=-(x+1)(x-1),
即y=-x2+1.
随堂练习
类型
基本形式
适用情况
一般式
顶点式
交点式
已知图象上任意三点
已知顶点坐标、对称轴、最值和其他条件.
已知抛物线与x轴的两个交点坐标和任一个点的坐标
方法归纳
二次函数的表达式的三种形式
用待定系数法求二次函数表达式的步骤:
(1)设出适当的二次函数表达式的形式;
(2)代入点的坐标得到方程(组);
(3)解方程(组)求出待定系数的值;
(4)写出所求二次函数的表达式式并化为一般形式.
1.已知二次函数的图象过点(2, 4),且当x=1时, y有最值为6,则该二次函数的表达式是 .
y=-2(x-1)2+6
随堂练习
2.如图,二次函数的图象过A、B、C三点,点A的坐标为(-1,0),点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC,则这个二次函数的表达式为 .
A
O
C
B
x
y
解:设所求二次函数的表达式是y=a(x+1)(x-4),
∵ AB=OC=5,
∴点C的坐标为(0,5),
∴ a(0+1)(0-4)=5,
解得:a= .
随堂练习
3.如图,当x=-1时,抛物线的最高点的纵坐标为4,
且与x轴两交点之间的距离为6,求抛物线的表达式.
O
x
y
解:依题意设该抛物线的表达式为y=a(x+1)2+4.
∵ 抛物线的对称轴为x=-1,
抛物线与x轴两交点之间的距离为6,
∴ 抛物线与x轴的交点分别为(-4,0),(2,0),
∴ 0=a(2+1)2+4,
解得:a= .
∴所求抛物线的表达式为
4.如图,抛物线y=x2+bx+c过点A(-4,-3),与
y轴交于点B,对称轴是x=-3,请解答下列问题:
(1)求抛物线的表达式;
解:(1)把点A(-4,-3)代入y=x2+bx+c
得:16-4b+c=-3,
∴ c-4b=-19.
∵对称轴是x=-3,
∴b=6,
∴c=5,
∴ 抛物线的表达式是y=x2+6x+5.
随堂练习
(2)若和x轴平行的直线与抛物线交于C,D两点,点C在对称轴左侧,且CD=8,求△BCD的面积.
(2)∵CD∥x轴,
∴点C与点D关于x=-3对称.
∵点C在对称轴左侧,且CD=8,
∴点C的横坐标为-7,
∴点C的纵坐标为(-7)2+6×(-7)+5=12.
∵点B的坐标为(0,5),
∴△BCD中CD边上的高为12-5=7,
∴△BCD的面积=
C
D
=28.
-7
①已知三点坐标
②已知顶点坐标或对称轴或最值
③已知抛物线与x轴的两个交点
已知条件
所选方法
用一般式法:y=ax2+bx+c
用顶点法:y=a(x-h)2+k
用交点法:y=a(x-x1)(x-x2)
(x1,x2为交点的横坐标)
待定系数法
求二次函数解析式
课堂小结
作业与课外学习任务
1.作业:课本P24 习题26.2 4,5
2.课外学习任务:
预习课本P26-29 26.3 实践与探索
教学反馈:
作业存在的主要问题:
3. 求二次函数的表达式
教学目标
教学重点与难点
重点:用待定系数法求二次函数的表达式.
难点:根据题目的已知条件,灵活选择合适的二次函数表达式.
1.掌握用待定系数法列方程组求二次函数解析式
的方法.
2.由已知条件的特点,灵活选择二次函数的两种形式,合理地设出函数解析式,可使计算过程更简便.
1.一次函数y=kx+b(k≠0)有几个待定系数?
通常需要已知几个点的坐标求出它的表达式?
2.求一次函数表达式的方法是什么?
它的一般步骤是什么?
2个
2个
待定系数法
(1)设:(表达式)
(2)代:(坐标代入)
(3)解:方程(组)
(4)还原:(写表达式)
复习引入
如果要求二次函数y=ax?+bx+c(a≠0)的表达式,
又需要几个条件呢?
例1 已知二次函数y=ax2 + c的图象经过点(2,3)
和(-1,-3),求这个二次函数的表达式.
解:∵该图象经过点(2,3)和(-1,-3),
3=4a+c,
-3=a+c,
∴所求二次函数表达式为 y=2x2-5.
∴{
a =2,
c =-5.
解得:
{
关于y轴对称
一.特殊条件的二次函数的表达式
学习新知
已知二次函数y=ax2 + bx的图象经过点(-2, 8)
和(-1,5),求这个二次函数的表达式.
解:∵该图象经过点(-2,8)和(-1,5) ,
图象经过原点
8=4a-2b,
5=a-b,
∴{
解得: a=-1,b=-6.
∴ 这个二次函数的表达式y=-x2-6x.
随堂练习
例2 已知二次函数的顶点是(-2, 1),且函数图象过点(1,-8),求这个二次函数的表达式.
解:设这个二次函数的表达式是y=a(x-h)2+k(a≠0),
∴ y=a(x+2)2+1,
∴ a(1+2)2+1=-8,
解得: a =-1.
∴所求二次函数的表达式是y=-(x+2)2+1或y=-x2-4x-3.
二.顶点法求二次函数的表达式
∵ 这个二次函数的顶点是(-2, 1),
∵ 函数图象过点(1, -8),
学习新知
顶点法求二次函数的表达式的步骤
①设函数表达式是y=a(x-h)2+k (a≠0);
方法总结
②先代入顶点坐标,得到关于a的一元一次方程;
③将另一点的坐标代入原方程求出a值;
④a用数值换掉,写出函数表达式.
(函数表达式的结果可以用顶点式或一般式表示)
例3 一个二次函数的图象经点 (0, 1),它的顶点坐标为(8,9),
求这个二次函数的表达式.
例题精析
解: ∵这个二次函数的图象的顶点坐标为(8,9),
∴ 设函数的表达式为y=a(x-8)2+9(a≠0).
又∵ 函数的图象经过点(0 ,1),
∴ 0=a(0-8)2+9.
解得:a= .
∴所求的二次函数的表达式是
1.抛物线的顶点在原点,且抛物线经过点(2,8),
求它的表达式.
随堂练习
解:∵抛物线的顶点在原点,
∴ 设它的表达式为y=ax2(a≠0).
∵ 抛物线经过点(2,8),
∴ 8=a×22,
∴ a=2.
∴ 所求抛物线的表达式为y=2x2.
2.抛物线的顶点坐标为(-1,-2),且抛物线经过
点(1,10),求该抛物线的表达式.
解: ∵抛物线的顶点坐标为(-1,-2),
∴ 设该抛物线的表达式为y=a(x+1)2-2(a≠0).
∵ 抛物线经过点(1,10),
∴ 10=a(1+1)2-2.
解得:a=3.
∴ 该抛物线的表达式为y=3(x+1)2-2.
即 y=3x2+6x+1.
学习新知
三.一般式法求二次函数的表达式
例4 一个二次函数的图象经过(0,1)、(2,4)、(3,10)三点,求这个二次函数的表达式.
解:设所求二次函数的表达式为y=ax2+bx+c,
∵ 函数的图象经过(0,1)、(2,4)、(3,10)三点,
解得:a= ,b= ,c= .
1
∴ 所求二次函数的表达式为
④把待定系数a,b,c用数字换掉,写出函数的表达式.
一般式法求二次函数的表达式的步骤
方法总结
①设函数的表达式为y=ax2+bx+c (a≠0) ;
②把已知点的坐标代入所设的表达式,得到一个
三元一次方程组;
③解方程组得到a,b,c的值;
随堂练习
1.已知抛物线y=ax2+bx+c经过三点:(-1,-1),(1,1),
(0,-2),求这条抛物线所对应的二次函数的表达式.
解:设所求二次函数的表达式为y=ax2+bx+c,
依题意得:
解得:a= ,b= ,c= .
-2
2
1
∴ 所求二次函数的表达式为y=2x2+x-2.
2.已知二次函数的图象经过(0, 3), (-2,-5), (1, 4),
求这个二次函数的表达式.
随堂练习
解:设所求二次函数的表达式为y=ax2+bx+c,
依题意得:
解得:a= ,b= ,c= .
3
-1
2
∴ 所求二次函数的表达式为y=-x2+2x+3.
交点法求二次函数的表达式的步骤
其步骤是:
①设函数的表达式是y=a(x-x1)(x-x2) (其中x1、x2为抛物线与x轴交点的横坐标;
②先把两交点的横坐标x1,x2代入到表达式中,得到关于a的一元一次方程;
③将已知的另一个条件代入方程求出a的值;
④a用数值换掉,写出函数表达式.
学习新知
知道抛物线与x轴的交点,求抛物线的表达式
的方法叫做交点法.
例题精析
例5 已知抛物线与x轴交于点A(-3,0)、B(5,0),
且与y轴交于点C(0, -15),求抛物线的解析式.
解:设所求抛物线的解析式是y=a(x+3)(x-5),
把点(0, -3)代入上式得:
a(0+3)(0-5)=-15,
解得:a= ,
1
∴ 所求抛物线的表达式为y=(x+3)(x-5),
即 y=x2-2x-15.
已知抛物线与x轴相交于点A(-1, 0),B(1, 0),且过点M(0,1),求此函数的表达式.
解:∵点A(-1,0),B(1,0)是图象与x轴的交点,
∴ 设二次函数的表达式为y=a(x+1)(x-1).
又∵抛物线过点M(0,1),
∴1=a(0+1)(0-1),
解得:a=-1,
∴所求抛物线的表达式为y=-(x+1)(x-1),
即y=-x2+1.
随堂练习
类型
基本形式
适用情况
一般式
顶点式
交点式
已知图象上任意三点
已知顶点坐标、对称轴、最值和其他条件.
已知抛物线与x轴的两个交点坐标和任一个点的坐标
方法归纳
二次函数的表达式的三种形式
用待定系数法求二次函数表达式的步骤:
(1)设出适当的二次函数表达式的形式;
(2)代入点的坐标得到方程(组);
(3)解方程(组)求出待定系数的值;
(4)写出所求二次函数的表达式式并化为一般形式.
1.已知二次函数的图象过点(2, 4),且当x=1时, y有最值为6,则该二次函数的表达式是 .
y=-2(x-1)2+6
随堂练习
2.如图,二次函数的图象过A、B、C三点,点A的坐标为(-1,0),点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC,则这个二次函数的表达式为 .
A
O
C
B
x
y
解:设所求二次函数的表达式是y=a(x+1)(x-4),
∵ AB=OC=5,
∴点C的坐标为(0,5),
∴ a(0+1)(0-4)=5,
解得:a= .
随堂练习
3.如图,当x=-1时,抛物线的最高点的纵坐标为4,
且与x轴两交点之间的距离为6,求抛物线的表达式.
O
x
y
解:依题意设该抛物线的表达式为y=a(x+1)2+4.
∵ 抛物线的对称轴为x=-1,
抛物线与x轴两交点之间的距离为6,
∴ 抛物线与x轴的交点分别为(-4,0),(2,0),
∴ 0=a(2+1)2+4,
解得:a= .
∴所求抛物线的表达式为
4.如图,抛物线y=x2+bx+c过点A(-4,-3),与
y轴交于点B,对称轴是x=-3,请解答下列问题:
(1)求抛物线的表达式;
解:(1)把点A(-4,-3)代入y=x2+bx+c
得:16-4b+c=-3,
∴ c-4b=-19.
∵对称轴是x=-3,
∴b=6,
∴c=5,
∴ 抛物线的表达式是y=x2+6x+5.
随堂练习
(2)若和x轴平行的直线与抛物线交于C,D两点,点C在对称轴左侧,且CD=8,求△BCD的面积.
(2)∵CD∥x轴,
∴点C与点D关于x=-3对称.
∵点C在对称轴左侧,且CD=8,
∴点C的横坐标为-7,
∴点C的纵坐标为(-7)2+6×(-7)+5=12.
∵点B的坐标为(0,5),
∴△BCD中CD边上的高为12-5=7,
∴△BCD的面积=
C
D
=28.
-7
①已知三点坐标
②已知顶点坐标或对称轴或最值
③已知抛物线与x轴的两个交点
已知条件
所选方法
用一般式法:y=ax2+bx+c
用顶点法:y=a(x-h)2+k
用交点法:y=a(x-x1)(x-x2)
(x1,x2为交点的横坐标)
待定系数法
求二次函数解析式
课堂小结
作业与课外学习任务
1.作业:课本P24 习题26.2 4,5
2.课外学习任务:
预习课本P26-29 26.3 实践与探索
教学反馈:
作业存在的主要问题:
