八年级数学人教版下册16.3 二根次式加减法1课件(共18张)
文档属性
| 名称 | 八年级数学人教版下册16.3 二根次式加减法1课件(共18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 390.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-26 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
第1课时
二次根式加减法
第十六章
二次根式
人教版
八年级下
16.3
二根次式
学习目标
1、掌握二次根式的加减法法则;(重点)
2、熟练地进行二次根式
的加减法运算.(难点)
情景引入
1、计算:
8+18=
?
今天我们一起来学习二次根式的加减法.
26
化简后被开方数相同
2、
满足什么条件的根式是最简二次根式?
3、
化简下列两组二次根式,每组化简后有什么共同特点?
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
问题
现有一块长为
、宽为
的木板,能否采用如图的方式,在这块木板上截出两个面积分别是
的正方形木板?
新知讲授
知识点一
同类二次根式
广东省怀集县梁村镇初级中学
周恒
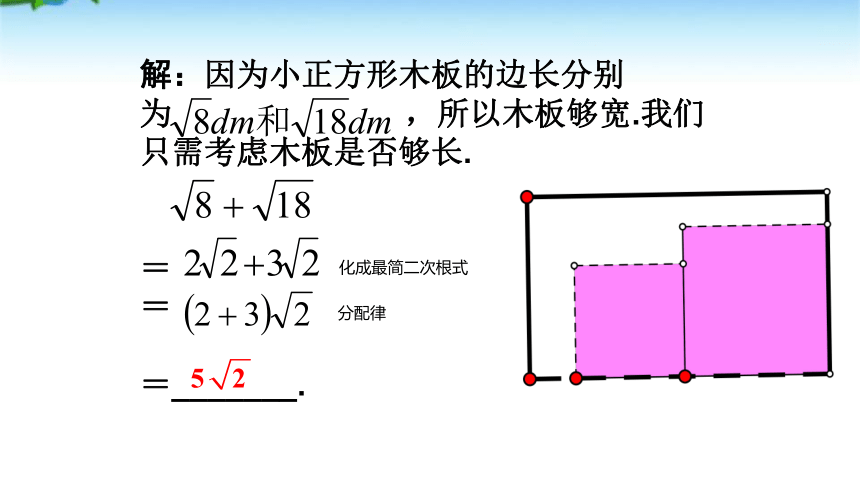
解:因为小正方形木板的边长分别
为
,所以木板够宽.我们只需考虑木板是否够长.
=
=
=_______.
化成最简二次根式
分配律
由
<1.5
得,
____
7.5,即两个正方形的边长的和小于木板的长,能按要求裁出木板.
结论:
和
化成最简二次根式
和
后,被开方数______________,像这样的二次根式就叫做同类二次根式.
<
相同(都是2)
几个二次根式化成最简二次根式后,若被开方数相同,则这几个二次根式就是同类二次根式.
下列各组二次根式中是同类二次根式的是(
)
练习
C
化成最简二次根式后发现:前两个式子为同类二次根式,可以合并;最后一个不是同类二次根式,不能合并.
下列各式能否合并
上面的问题中,利用________律将
和
进行合并.由此得,二次根式的加减法法则:二次根式加减时,可以先将二次根式化成______________
,再将
____________的二次根式进行_______.
分配
最简二次根式
被开方数相同
合并
知识点二
二次根式的加减法法则和运算
新知讲授
例1
计算:
解
典例精讲
计算(1)
;
(2)
.
解:⑴原式=
=
⑵原式=
=
=
练习
比较二次根式的加减与整式的加减,你能得出什么结论?
例2
计算:
“一化简二判断三合并”
(1)化——将非最简二次根式的二次根式化简;
加减法的运算步骤:
(2)找——找出被开方数相同的二次根式;
(3)并——把被开方数相同的二次根式合并.
总结归纳
×
×
√
不是同类二次根式,不能合并
课堂练习
(4)
(4)
×
不是同类二次根式,不能合并
2.计算:
3
计算3
-2
的结果是( )
A.
B.2
C.3
D.6
4.计算
(
)
A.
B.
C.3
D.
5.计算
的结果是(
)
A.
B.
C.
D.
A
A
B
第1课时
二次根式加减法
第十六章
二次根式
人教版
八年级下
16.3
二根次式
学习目标
1、掌握二次根式的加减法法则;(重点)
2、熟练地进行二次根式
的加减法运算.(难点)
情景引入
1、计算:
8+18=
?
今天我们一起来学习二次根式的加减法.
26
化简后被开方数相同
2、
满足什么条件的根式是最简二次根式?
3、
化简下列两组二次根式,每组化简后有什么共同特点?
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
问题
现有一块长为
、宽为
的木板,能否采用如图的方式,在这块木板上截出两个面积分别是
的正方形木板?
新知讲授
知识点一
同类二次根式
广东省怀集县梁村镇初级中学
周恒
解:因为小正方形木板的边长分别
为
,所以木板够宽.我们只需考虑木板是否够长.
=
=
=_______.
化成最简二次根式
分配律
由
<1.5
得,
____
7.5,即两个正方形的边长的和小于木板的长,能按要求裁出木板.
结论:
和
化成最简二次根式
和
后,被开方数______________,像这样的二次根式就叫做同类二次根式.
<
相同(都是2)
几个二次根式化成最简二次根式后,若被开方数相同,则这几个二次根式就是同类二次根式.
下列各组二次根式中是同类二次根式的是(
)
练习
C
化成最简二次根式后发现:前两个式子为同类二次根式,可以合并;最后一个不是同类二次根式,不能合并.
下列各式能否合并
上面的问题中,利用________律将
和
进行合并.由此得,二次根式的加减法法则:二次根式加减时,可以先将二次根式化成______________
,再将
____________的二次根式进行_______.
分配
最简二次根式
被开方数相同
合并
知识点二
二次根式的加减法法则和运算
新知讲授
例1
计算:
解
典例精讲
计算(1)
;
(2)
.
解:⑴原式=
=
⑵原式=
=
=
练习
比较二次根式的加减与整式的加减,你能得出什么结论?
例2
计算:
“一化简二判断三合并”
(1)化——将非最简二次根式的二次根式化简;
加减法的运算步骤:
(2)找——找出被开方数相同的二次根式;
(3)并——把被开方数相同的二次根式合并.
总结归纳
×
×
√
不是同类二次根式,不能合并
课堂练习
(4)
(4)
×
不是同类二次根式,不能合并
2.计算:
3
计算3
-2
的结果是( )
A.
B.2
C.3
D.6
4.计算
(
)
A.
B.
C.3
D.
5.计算
的结果是(
)
A.
B.
C.
D.
A
A
B
