七年级数学人教版下册立方根第2课时(共21张)
文档属性
| 名称 | 七年级数学人教版下册立方根第2课时(共21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 568.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-26 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
七年级下册(RJ)
6.2
立方根(第2课时)
自主学习反馈
完成率反馈,表扬优秀学生;由平台数据,找到共性和个性问题。
表扬:课前检测正确率高的学生:图片展示
学案书写工整的学生:图片展示(主要是学案上主观题书写规范展示)
课前检测和学案整体完成情况较好的学生:图片展示(课前自主学习整体完成优秀展示)
问题:共性典型问题:图片展示(课前自主学习中两个或者至多三个典型共性问题的展示)
个性典型问题:图片展示(课前自主学习中两个或者至多三个典型个性问题的展示)
学习目标
1.进一步理解立方根的概念,并能熟练地进行求一个数的立方根的运算;
2.能用有理数估计一个无理数的大致范围,形成估算意识,培养估算能力;
3.经历运用计算器探求数学规律的过程,发展合情推理能力,激发探索数学的兴趣.
自学检测
知识点1:开立方
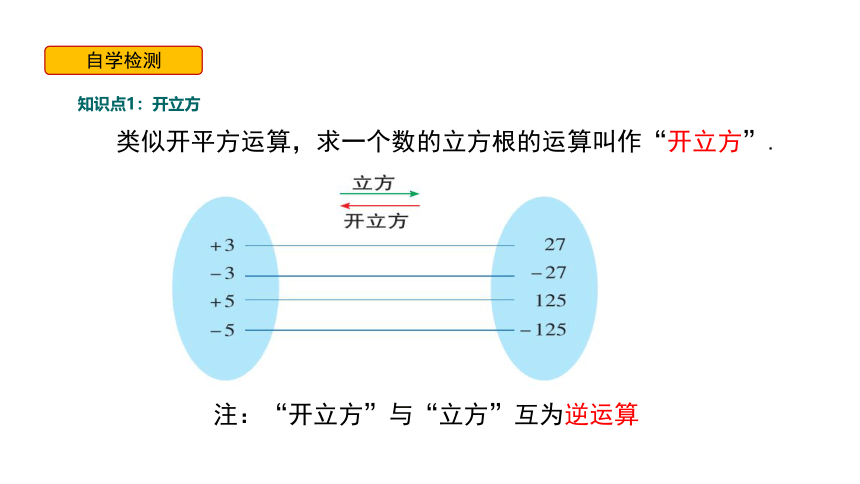
类似开平方运算,求一个数的立方根的运算叫作“开立方”.
注:“开立方”与“立方”互为逆运算
你能归纳出立方根的另一性质吗?
同类型检测
因为
=
,
所以
因为
所以
-2
=
=
-2
-3
-3
活动形式:随机选择一个同学回答,学生评判对错,答对,其他同学说:“YES”,答错说“NO”。全员参与,调动课堂气氛,激发学生学习兴。
自学检测
知识点2:立方根的性质
一般地,
=
自学释疑、拓展提升
学生典型问题点评:
学生课前4、5、6三小题问题图片展示
教师提问课前做错学生
活动形式:教师提问课前做错学生
巩固提升
要求:学生独立完成学案“课上学习”部分1、2、3题,拍照上传,互批纠错。
1、判断题
(1)64的立方根是
=
(
)
(2)
是
的立方根
(
)
(3)
(
)
(4)立方根等于它本身的数是0和1(
)
巩固提升
要求:学生独立完成学案“课上学习”部分1、2题,拍照上传,互批纠错。
3、
计算:
.
解:原式=3+2-(-1)
=5+1=6.
2、
的算术平方根是
.
2
自学检测
知识点3:用计算器求立方根
4
、用计算器求下列各数的立方根:343,-1.331.
解:依次按键:
显示:7
所以,
2ndF
4
3
3
=
依次按键:
显示:-1.1
所以,
2ndF
1
-
.
3
1
3
=
由于一个数的立方根可能是无限不循环小数,所以我们可以利用计算器求一个数的立方根或它的近似值.
不同的计算器的按键方式
可能有所差别!
5、用计算器求
的近似值(精确到0.001).
解
依次按键:
显示:1.259
921
05
所以,
2ndF
=
2
6、(1)利用计算器计算,并将计算结果填在表中,你发现了什么规律?
(2)用计算器计算
(结果精确到0.001)。并利用你发现的规律写出
,
,
的近似值。
要求:学生独立完成学案“课上学习”部分1、2题,拍照上传,互批纠错。
被开方数的小数点向左移动3n位(n为正整数)
被开方数的小数点向右移动3n位(n为正整数)
立方根的小数点就相应的向
???移动??
?
位
立方根的小数点就相应的向??
????
移动
位
6、(1)利用计算器计算,并将计算结果填在表中,你发现了什么规律?
(2)用计算器计算
(结果精确到0.001)。并利用你发现的规律写出
,
,
的近似值。
解:利用计算器得:
所以
被开方数的小数点向左移动3n位(n为正整数)
被开方数的小数点向右移动3n位(n为正整数)
立方根的小数点就相应的向
左
移动
n
位
0.
06
0.
6
6
60
立方根的小数点就相应的向
右
移动
n
位
≈4.642
≈0.04642
≈0.4642
≈40.642
被开方数的小数点向左或向右移动3n位时,立方根的小数点就相应的向左或向右移动n位(n为正整数).
总结归纳
巩固提升
要求:
1、学生独立完成学案“课上学习”部分第7题;
2、小组成员全部完成,抢答第一同学上台讲解。
7.比较3,4,
的大小.
解:33
=
27,43
=
64
因为27
<
50
<
64
所以3
<
<
4
巩固提升
要求:
1、学生独立完成学案“课上学习”部分第8题;
2、小组成员全部完成,抢答第一同学上台讲解。
8.比较下列各组数的大小.
(1)
与2.5;
(2)
与
.
解:因为
=
9
2.53
=
15.625
所以
<
15.625
所以
<
2.5
因为
=
3
所以
3
<
所以
<
拓展提升
要求:
1、学生独立完成学案“课上学习”部分第9题;
2、小组成员全部完成,抢答第一同学上台讲解。
9.若
=2,
=4,求
的值.
解:∵
=2,
=4.
∴x
=
23,y2
=
16,
∴x
=
8,y
=
±4.
∴x
+
2y
=
8
+
2×4
=
16
或
x
+
2y
=
8
–
2×4
=
0.
∴
=
=
4
或
=
=
0.
课堂总结
结论2
结论1
立方根
被开方数的小数点向左或向右移动3n位时立方根的小数点就相应的向左或向右移动n位(n为正整数).
1
2
3
积
分
榜
课堂总结
课后提升
解:一个正方体的体积变为原来的8倍,它的棱长变为原来的2倍;体积变为原来的27倍,它的棱长变为原来的3倍;体积变为原来的1
000倍,它的棱长变为原来的10倍;体积变为原来的n倍,它的棱长变为原来的倍.
11.
一个正方体的体积变为原来的8倍,它的棱长变为原来的多少倍?体积变为原来的27倍,它的棱长变为原来的多少倍?体积变为原来的1
000倍,它的棱长变为原来的多少倍?体积变为原来的n倍呢?
?
解:∵
∴
∴
10.若
,求
的值。
七年级下册(RJ)
6.2
立方根(第2课时)
自主学习反馈
完成率反馈,表扬优秀学生;由平台数据,找到共性和个性问题。
表扬:课前检测正确率高的学生:图片展示
学案书写工整的学生:图片展示(主要是学案上主观题书写规范展示)
课前检测和学案整体完成情况较好的学生:图片展示(课前自主学习整体完成优秀展示)
问题:共性典型问题:图片展示(课前自主学习中两个或者至多三个典型共性问题的展示)
个性典型问题:图片展示(课前自主学习中两个或者至多三个典型个性问题的展示)
学习目标
1.进一步理解立方根的概念,并能熟练地进行求一个数的立方根的运算;
2.能用有理数估计一个无理数的大致范围,形成估算意识,培养估算能力;
3.经历运用计算器探求数学规律的过程,发展合情推理能力,激发探索数学的兴趣.
自学检测
知识点1:开立方
类似开平方运算,求一个数的立方根的运算叫作“开立方”.
注:“开立方”与“立方”互为逆运算
你能归纳出立方根的另一性质吗?
同类型检测
因为
=
,
所以
因为
所以
-2
=
=
-2
-3
-3
活动形式:随机选择一个同学回答,学生评判对错,答对,其他同学说:“YES”,答错说“NO”。全员参与,调动课堂气氛,激发学生学习兴。
自学检测
知识点2:立方根的性质
一般地,
=
自学释疑、拓展提升
学生典型问题点评:
学生课前4、5、6三小题问题图片展示
教师提问课前做错学生
活动形式:教师提问课前做错学生
巩固提升
要求:学生独立完成学案“课上学习”部分1、2、3题,拍照上传,互批纠错。
1、判断题
(1)64的立方根是
=
(
)
(2)
是
的立方根
(
)
(3)
(
)
(4)立方根等于它本身的数是0和1(
)
巩固提升
要求:学生独立完成学案“课上学习”部分1、2题,拍照上传,互批纠错。
3、
计算:
.
解:原式=3+2-(-1)
=5+1=6.
2、
的算术平方根是
.
2
自学检测
知识点3:用计算器求立方根
4
、用计算器求下列各数的立方根:343,-1.331.
解:依次按键:
显示:7
所以,
2ndF
4
3
3
=
依次按键:
显示:-1.1
所以,
2ndF
1
-
.
3
1
3
=
由于一个数的立方根可能是无限不循环小数,所以我们可以利用计算器求一个数的立方根或它的近似值.
不同的计算器的按键方式
可能有所差别!
5、用计算器求
的近似值(精确到0.001).
解
依次按键:
显示:1.259
921
05
所以,
2ndF
=
2
6、(1)利用计算器计算,并将计算结果填在表中,你发现了什么规律?
(2)用计算器计算
(结果精确到0.001)。并利用你发现的规律写出
,
,
的近似值。
要求:学生独立完成学案“课上学习”部分1、2题,拍照上传,互批纠错。
被开方数的小数点向左移动3n位(n为正整数)
被开方数的小数点向右移动3n位(n为正整数)
立方根的小数点就相应的向
???移动??
?
位
立方根的小数点就相应的向??
????
移动
位
6、(1)利用计算器计算,并将计算结果填在表中,你发现了什么规律?
(2)用计算器计算
(结果精确到0.001)。并利用你发现的规律写出
,
,
的近似值。
解:利用计算器得:
所以
被开方数的小数点向左移动3n位(n为正整数)
被开方数的小数点向右移动3n位(n为正整数)
立方根的小数点就相应的向
左
移动
n
位
0.
06
0.
6
6
60
立方根的小数点就相应的向
右
移动
n
位
≈4.642
≈0.04642
≈0.4642
≈40.642
被开方数的小数点向左或向右移动3n位时,立方根的小数点就相应的向左或向右移动n位(n为正整数).
总结归纳
巩固提升
要求:
1、学生独立完成学案“课上学习”部分第7题;
2、小组成员全部完成,抢答第一同学上台讲解。
7.比较3,4,
的大小.
解:33
=
27,43
=
64
因为27
<
50
<
64
所以3
<
<
4
巩固提升
要求:
1、学生独立完成学案“课上学习”部分第8题;
2、小组成员全部完成,抢答第一同学上台讲解。
8.比较下列各组数的大小.
(1)
与2.5;
(2)
与
.
解:因为
=
9
2.53
=
15.625
所以
<
15.625
所以
<
2.5
因为
=
3
所以
3
<
所以
<
拓展提升
要求:
1、学生独立完成学案“课上学习”部分第9题;
2、小组成员全部完成,抢答第一同学上台讲解。
9.若
=2,
=4,求
的值.
解:∵
=2,
=4.
∴x
=
23,y2
=
16,
∴x
=
8,y
=
±4.
∴x
+
2y
=
8
+
2×4
=
16
或
x
+
2y
=
8
–
2×4
=
0.
∴
=
=
4
或
=
=
0.
课堂总结
结论2
结论1
立方根
被开方数的小数点向左或向右移动3n位时立方根的小数点就相应的向左或向右移动n位(n为正整数).
1
2
3
积
分
榜
课堂总结
课后提升
解:一个正方体的体积变为原来的8倍,它的棱长变为原来的2倍;体积变为原来的27倍,它的棱长变为原来的3倍;体积变为原来的1
000倍,它的棱长变为原来的10倍;体积变为原来的n倍,它的棱长变为原来的倍.
11.
一个正方体的体积变为原来的8倍,它的棱长变为原来的多少倍?体积变为原来的27倍,它的棱长变为原来的多少倍?体积变为原来的1
000倍,它的棱长变为原来的多少倍?体积变为原来的n倍呢?
?
解:∵
∴
∴
10.若
,求
的值。
