1.4线段、角的对称性

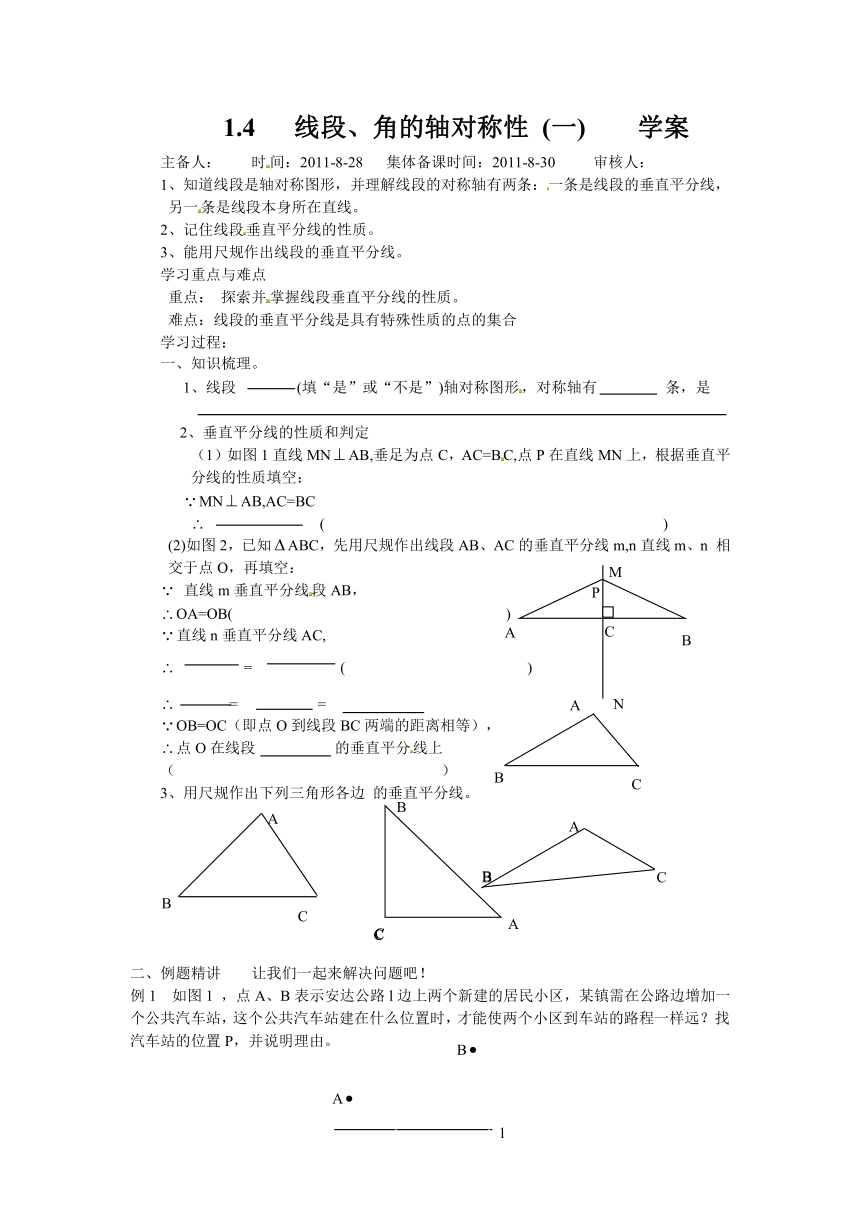
1.4 线段、角的轴对称性 (一) 学案
主备人： 时间：2011-8-28 集体备课时间：2011-8-30 审核人：
1、知道线段是轴对称图形，并理解线段的对称轴有两条：一条是线段的垂直平分线，另一条是线段本身所在直线。
2、记住线段垂直平分线的性质。
3、能用尺规作出线段的垂直平分线。
学习重点与难点
重点： 探索并掌握线段垂直平分线的性质。
难点：线段的垂直平分线是具有特殊性质的点的集合
学习过程：
知识梳理。
1、线段 (填“是”或“不是”)轴对称图形，对称轴有 条，是
2、垂直平分线的性质和判定
（1）如图1直线MNAB,垂足为点C，AC=BC,点P在直线MN上，根据垂直平分线的性质填空：
MNAB,AC=BC
( )
(2)如图2，已知ABC，先用尺规作出线段AB、AC的垂直平分线m,n直线m、n 相交于点O，再填空：
直线m垂直平分线段AB，
OA=OB( )
直线n垂直平分线AC,
= ( )
= =
OB=OC（即点O到线段BC两端的距离相等），
点O在线段 的垂直平分线上
（ ）
3、用尺规作出下列三角形各边 的垂直平分线。
二、例题精讲 让我们一起来解决问题吧！
例1 如图1 ，点A、B表示安达公路l边上两个新建的居民小区，某镇需在公路边增加一个公共汽车站，这个公共汽车站建在什么位置时，才能使两个小区到车站的路程一样远？找汽车站的位置P，并说明理由。
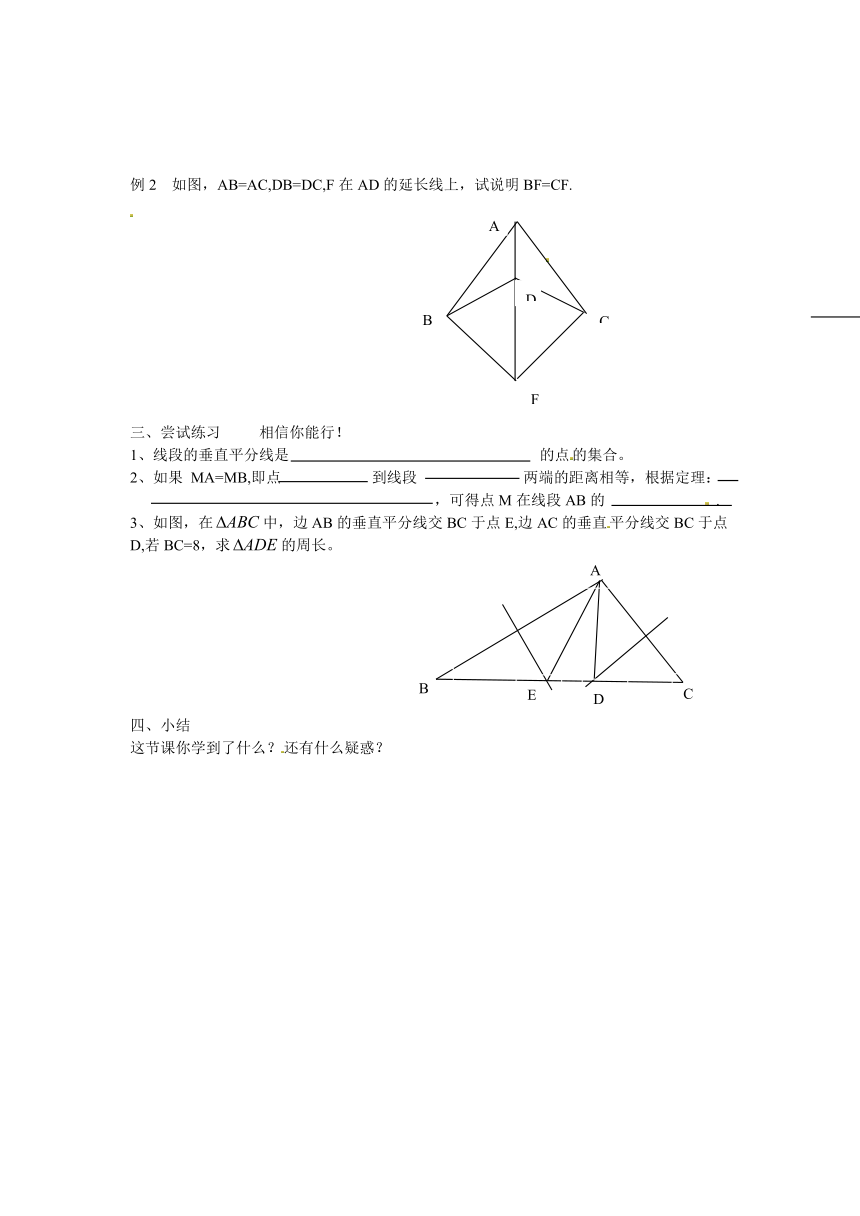
例2 如图，AB=AC,DB=DC,F在AD的延长线上，试说明BF=CF.
三、尝试练习 相信你能行！
1、线段的垂直平分线是 的点的集合。
2、如果 MA=MB,即点 到线段 两端的距离相等，根据定理：
，可得点M在线段AB的 .
3、如图，在中，边AB的垂直平分线交BC于点E,边AC的垂直平分线交BC于点D,若BC=8，求的周长。
四、小结
这节课你学到了什么？还有什么疑惑？
1.4 线段、角的对称性（二）
学习目标：
能用角的平分线的性质解决一些实际问题。
记住角的平分线是具有特殊性质的点的集合。
学习重点与难点：
重点：掌握角平分线的性质。
难点：理解角的平分线是具有特殊性质的点的集合。
学习过程：
知识梳理
角的轴对称性
角 (填“是”或“不是”)轴对称图形，对称轴是 。
2、角平分线的性质与判断
（1）如图1，OE平分,P是OE上的一点，PC,PD，垂足分别为点C、D,根据角平分线的性质填空：
OE平分, PC,PD,
（　　　　　　　　　　　　　　）
（２）如图２，已知，先作出、的平分线，相交于点Ｏ，过点Ｏ作ＯＤ，ＯＥ，ＯＦ，垂足分别为Ｄ、Ｅ、Ｆ，再填空：
ＢＯ平分，ＯＤ，ＯＥ，
ＯＤ＝ＯＥ（　　　　　　　　　　　　　　　）
ＣＯ平分，ＯＥ，ＯＦ，
= ( )
= =
即三角形的角平分线的交点到三边的距离相等。
ＯＤ＝ＯＦ，ＯＤＯＦ（　　），
点在 　的平分线上（　　　　　　　　　　　　　　　）
３、角平分线作图的简单应用
“西气东输”是造福子孙后代的创世工程，现有两条高速公路ｌ、ｌ和两个城镇Ａ、Ｂ（如图３），准备建一个燃气控制中心站Ｐ，使中心站到两条公路的距离相等，并且到两个城市的距离相等，请你画出中心站的位置。（保留画图痕迹，不写作法）
　　　　　　
　　　　　　　　　　　　　
例1 如图，AD是的角平分线，DE、DF分别是、的高。试说明AD垂直平分EF.
三、尝试练习
1、到三角形三边距离相等的点是 （ ）
A 三条高的交点 B 三条中线的交点
C 三条垂直平分线的交点 D三条内角平分线的交点
2、如图，在中，,AD平分,CD=5,则点D到AB的距离为
四、小结
这节课你学到了什么？还有什么疑惑？
P
M
C
B
A
A
N
C
B
B
C
C
C
C
A
A
B
C
A
B
B
B
A
l
A
C
D
F
F
B
D
E
B
C
A
A
N
A
A
l
B
l
ｌ EMBED Equation.3 EMBED Equation.3
B
C
F
E
A
D
D
C
2题
A
B
A