2020-2021学年八年级数学人教版下册课件-17.1 勾股定理(21张)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册课件-17.1 勾股定理(21张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 981.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-27 00:00:00 | ||
图片预览






文档简介
17.1.1 勾股定理
?小问题-大现象-善抽象
一、情境导入 古韵今风?
1000多年前,中国人发明了七巧板,外国人称之为“中国魔板”、“唐图”。
学习目标:
1、掌握勾股定理,能运用勾股定理进行简单的计算。
2、体会勾股定理的探索和验证过程,发展推理能力,初步领会用数形结合的思想以及面积方法解决几何问题的基本思路。
3、介绍我国古代在勾股定理研究方面所取得的成就,激发学生热爱祖国悠久文化的情感。
?特殊-一般-猜想
a
a
c
活动一:
用四张全等的等腰直角三角形纸片 拼成一个正方形(不能重叠,不能有空隙)
二、追溯历史 解密真相
你能用拼得的正方形得到c和a之间的关系吗?
a
a
c
c
c?=2a?
c?=a?+a?
等腰直角三角形的三边之间的关系:
斜边的平方的等于两直角边的平方和
对于一般的直角三角形,三边之间有什么关系呢?
你能用拼得的正方形得到c和a之间的关系吗?
A
B
C
C
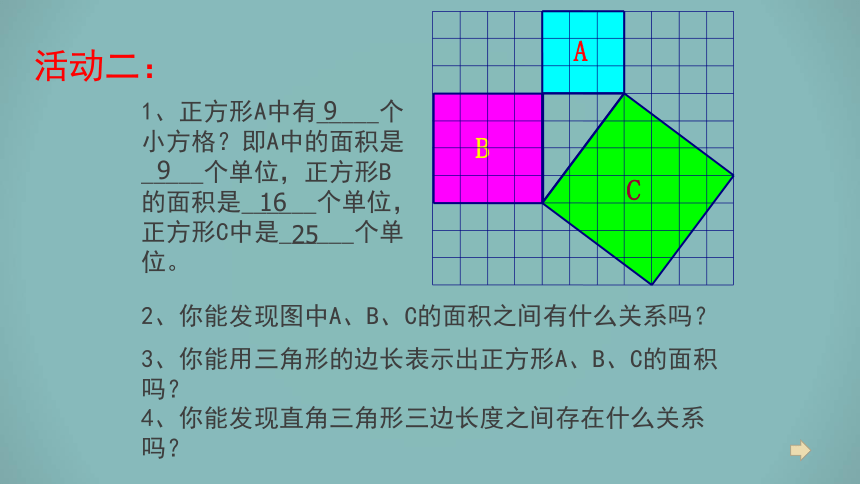
1、正方形A中有_____个小方格?即A中的面积是_____个单位,正方形B的面积是______个单位,正方形C中是______个单位。
2、你能发现图中A、B、C的面积之间有什么关系吗?
3、你能用三角形的边长表示出正方形A、B、C的面积吗?
4、你能发现直角三角形三边长度之间存在什么关系吗?
9
9
16
25
活动二:
A
B
C
C
A
B
C
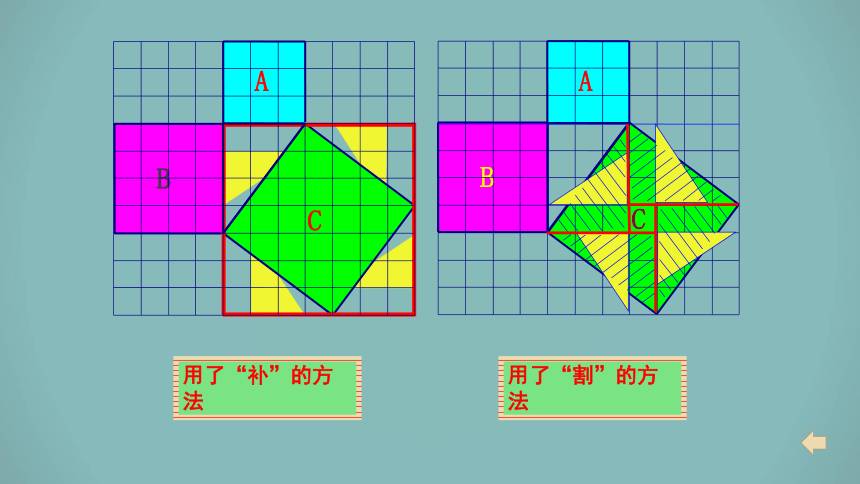
用了“割”的方法
用了“补”的方法
a
b
c
活动三:
用四张全等的直角三角形纸片拼成一个正方形(不能重叠,允许有空隙)
你能用拼得的正方形得到三角形三边a,b,c之间的关系吗?
三、推陈出新 借古鼎今
勾股定理:
如果直角三角形两直角边分别为a、b,
斜边为c,那么 a2+b2=c2
定理文字表达 :直角三角形两直角边的平方和等于斜边的平方.
a
b
c
人类最伟大的十个科学发现之一
几何语言:
在Rt△ABC中,∠C=90°,由勾股定理得:a?+b?=c?(AC?+BC?=AB?)
A
B
C
1、已知在Rt△ABC中,∠C=90°
(1)若a=5,b=12,则c=_____
(2)若c=10,b=8,则a=______
(3)若a:c=3:5,b=2,则a=_____,c=_____.
2、已知直角三角形的两边长分别为3cm和5cm,则第三边长为________.
3.已知直角三角形中30°角所对得直角边长为3,则另一条直角边长为_____.
13
6
四、取其精华 古为今用
我国古代把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”。据《周髀算经》记载,三千多年前,周朝数学家商高就发现了“勾三股四弦五”的结论,这正是勾股定理的一个特例。
中国古代数学家中,最早对勾股定理进行证明的,是三国时期吴国的赵爽,他创制了一幅“勾股圆方图”,用数形结合的方法,给出了勾股定理的详细证明。2002年在北京召开的国际数学家大会,会标就是以赵爽弦图为基础设计的,其在中国数学史上的地位可见一般。
?勾股史话
两千多年前,古希腊毕达哥拉斯学派也发现了勾股定理,因此在国外称该定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年,希腊曾发行了一枚纪念邮票,如图所示。
勾股定理是几何学的明珠,所以它充满魅力,其证明方法十分丰富,达数百种之多,同学们如果感兴趣的话,不妨自己动手,搜集更多的有关勾股定理的资料。
青朱出入图
?勾股史话
1、邮票中的图案是怎样构成的?
2、各个正方形面积之间有什么数量关系?你是怎样得到的?
较小的两个正方形面积之和等于最大的正方形的面积
81
144
x
169
144
y
练习1:求图中x,y的值。
看谁算得快
练习2:已知S1=1,S2=3, S3=2,S4=4 , 求S5 、S6 、S7的值.
看谁算得快
s3
1
1
美丽的勾股树
谈谈本节课你有哪些收获?
五、温故后思 任务顺延
六、布置作业 拓展新知
1、书P24页练习1、2(必做题)
2、书P30页 美国第20任总统詹姆斯.加菲尔德的用两个全等的等腰直角三角形拼图证明了勾股定理,你知道他是如何证明的呢?(选做题)
当堂检测
1.如图1,学校有一块长方形花圃,有极少数人为了避开拐角走“捷 径”,在花圃内走出了一条“路”.他们仅仅少走了_____ 步路(假设2步为1m),却踩伤了花草.
2.如图2,在Rt△ABC中,∠C=90°, BC= .
3.若直角三角形的两边长分别为3cm、4cm,则第三边长( ).
图1
图2
4
12
C
拓展提高
图1
图2
1.如图1,分别以Rt△ABC的三边为直径作半圆,其
面积分别为S、S、S,且S= ,S= ,则S= 。
2.如图2,在直线同侧有三个正方形a、b、c,若a、c
的面积分别是5和12,则b的面积为 。
感谢大家
?小问题-大现象-善抽象
一、情境导入 古韵今风?
1000多年前,中国人发明了七巧板,外国人称之为“中国魔板”、“唐图”。
学习目标:
1、掌握勾股定理,能运用勾股定理进行简单的计算。
2、体会勾股定理的探索和验证过程,发展推理能力,初步领会用数形结合的思想以及面积方法解决几何问题的基本思路。
3、介绍我国古代在勾股定理研究方面所取得的成就,激发学生热爱祖国悠久文化的情感。
?特殊-一般-猜想
a
a
c
活动一:
用四张全等的等腰直角三角形纸片 拼成一个正方形(不能重叠,不能有空隙)
二、追溯历史 解密真相
你能用拼得的正方形得到c和a之间的关系吗?
a
a
c
c
c?=2a?
c?=a?+a?
等腰直角三角形的三边之间的关系:
斜边的平方的等于两直角边的平方和
对于一般的直角三角形,三边之间有什么关系呢?
你能用拼得的正方形得到c和a之间的关系吗?
A
B
C
C
1、正方形A中有_____个小方格?即A中的面积是_____个单位,正方形B的面积是______个单位,正方形C中是______个单位。
2、你能发现图中A、B、C的面积之间有什么关系吗?
3、你能用三角形的边长表示出正方形A、B、C的面积吗?
4、你能发现直角三角形三边长度之间存在什么关系吗?
9
9
16
25
活动二:
A
B
C
C
A
B
C
用了“割”的方法
用了“补”的方法
a
b
c
活动三:
用四张全等的直角三角形纸片拼成一个正方形(不能重叠,允许有空隙)
你能用拼得的正方形得到三角形三边a,b,c之间的关系吗?
三、推陈出新 借古鼎今
勾股定理:
如果直角三角形两直角边分别为a、b,
斜边为c,那么 a2+b2=c2
定理文字表达 :直角三角形两直角边的平方和等于斜边的平方.
a
b
c
人类最伟大的十个科学发现之一
几何语言:
在Rt△ABC中,∠C=90°,由勾股定理得:a?+b?=c?(AC?+BC?=AB?)
A
B
C
1、已知在Rt△ABC中,∠C=90°
(1)若a=5,b=12,则c=_____
(2)若c=10,b=8,则a=______
(3)若a:c=3:5,b=2,则a=_____,c=_____.
2、已知直角三角形的两边长分别为3cm和5cm,则第三边长为________.
3.已知直角三角形中30°角所对得直角边长为3,则另一条直角边长为_____.
13
6
四、取其精华 古为今用
我国古代把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”。据《周髀算经》记载,三千多年前,周朝数学家商高就发现了“勾三股四弦五”的结论,这正是勾股定理的一个特例。
中国古代数学家中,最早对勾股定理进行证明的,是三国时期吴国的赵爽,他创制了一幅“勾股圆方图”,用数形结合的方法,给出了勾股定理的详细证明。2002年在北京召开的国际数学家大会,会标就是以赵爽弦图为基础设计的,其在中国数学史上的地位可见一般。
?勾股史话
两千多年前,古希腊毕达哥拉斯学派也发现了勾股定理,因此在国外称该定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年,希腊曾发行了一枚纪念邮票,如图所示。
勾股定理是几何学的明珠,所以它充满魅力,其证明方法十分丰富,达数百种之多,同学们如果感兴趣的话,不妨自己动手,搜集更多的有关勾股定理的资料。
青朱出入图
?勾股史话
1、邮票中的图案是怎样构成的?
2、各个正方形面积之间有什么数量关系?你是怎样得到的?
较小的两个正方形面积之和等于最大的正方形的面积
81
144
x
169
144
y
练习1:求图中x,y的值。
看谁算得快
练习2:已知S1=1,S2=3, S3=2,S4=4 , 求S5 、S6 、S7的值.
看谁算得快
s3
1
1
美丽的勾股树
谈谈本节课你有哪些收获?
五、温故后思 任务顺延
六、布置作业 拓展新知
1、书P24页练习1、2(必做题)
2、书P30页 美国第20任总统詹姆斯.加菲尔德的用两个全等的等腰直角三角形拼图证明了勾股定理,你知道他是如何证明的呢?(选做题)
当堂检测
1.如图1,学校有一块长方形花圃,有极少数人为了避开拐角走“捷 径”,在花圃内走出了一条“路”.他们仅仅少走了_____ 步路(假设2步为1m),却踩伤了花草.
2.如图2,在Rt△ABC中,∠C=90°, BC= .
3.若直角三角形的两边长分别为3cm、4cm,则第三边长( ).
图1
图2
4
12
C
拓展提高
图1
图2
1.如图1,分别以Rt△ABC的三边为直径作半圆,其
面积分别为S、S、S,且S= ,S= ,则S= 。
2.如图2,在直线同侧有三个正方形a、b、c,若a、c
的面积分别是5和12,则b的面积为 。
感谢大家
