2020-2021学年人教版七年级数学下册5.2.2平行线判定方法的综合运用课件(17张)
文档属性
| 名称 | 2020-2021学年人教版七年级数学下册5.2.2平行线判定方法的综合运用课件(17张) |  | |
| 格式 | pptx | ||
| 文件大小 | 571.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-27 00:32:12 | ||
图片预览






文档简介
七年级下册(RJ)
平行线判定方法的综合运用
自主学习反馈
完成率反馈,表扬优秀学生;由平台数据,找到共性和个性问题。
表扬:课前检测正确率高的学生:图片展示
学案书写工整的学生:图片展示(主要是学案上主观题书写规范展示)
课前检测和学案整体完成情况较好的学生:图片展示(课前自主学习整体完成优秀展示)
问题:共性典型问题:图片展示(课前自主学习中两个或者至多三个典型共性问题的展示)
个性典型问题:图片展示(课前自主学习中两个或者至多三个典型个性问题的展示)
学习目标
1.进一步掌握平行线的判定方法,并会运用平行线的
判定解决问题;(重点)
2.掌握垂直于同一条直线的两条直线互相平行.
自学释疑、拓展提升
知识点一:?平行线的判定的综合运用
自学问题:不能准确的选择平行线判定方法,书写不规范
学生典型问题展示:(学生课前问题图片展示)错误率较高习题和学案练习题。
解决方式:教师问题引导,学生组内或组间讨论,以小组为单位展示. 同学或教师
及时评价展示过程中暴露的问题.
(3)如果∠D+∠DFE=180°,可以判断哪两条直线平行?为什么?
例1 如图,E是AB上一点,F是DC上一点,G是BC延长线上一点.
(1)如果∠B=∠DCG,可以判断哪两条直线平行?为什么?
(2)如果∠D=∠DCG,可以判断哪两条直线平行? 为什么?
A
B
D
C
E
F
G
解 (1)AB//CD, 同位角相等,两直线平行;
(2)AD//BC, 内错角相等,两直线平行;
(3)AD//EF, 同旁内角互补,两直线平行.
活动形式:抢答,前三名同学到讲台讲解,其他学生聆听纠错。
巩固练习
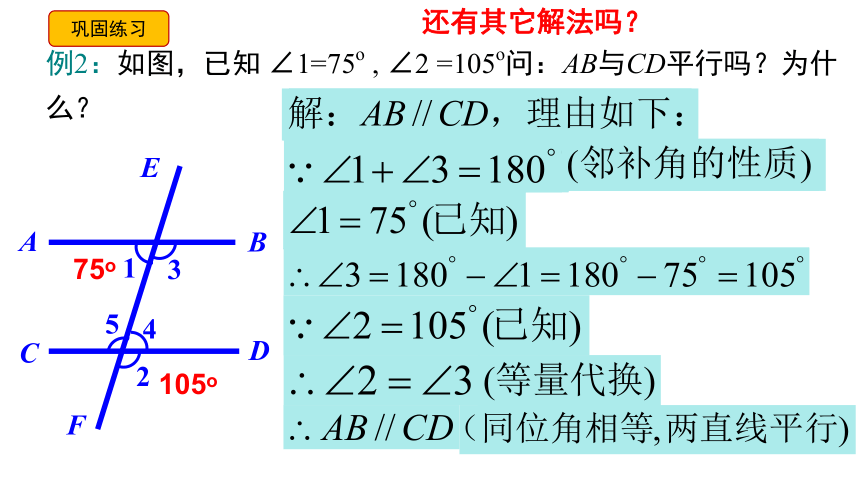
例2:如图,已知 ∠1=75o , ∠2 =105o问:AB与CD平行吗?为什么?
A
C
1
4
2
3
B
D
5
F
E
75o
105o
还有其它解法吗?
巩固练习
例2:如图,已知 ∠1=75o , ∠2 =105o问:AB与CD平行吗?为什么?
A
C
1
4
2
3
B
D
5
F
E
75o
105o
巩固练习
例3 如图,∠1=∠2,能判断AB∥DF吗?为什么?
?
?
?
?
?
?
F
D
C
A
B
E
1
2
解:不能.
添加∠CBD=∠EDB
内错角相等,两直线平行
若不能判断AB∥DF,你认为还需要再添加的一个条件是什么呢?写出这个条件,并说明你的理由.
巩固练习
要求:学生独立完成学案“课上学习”部分3题,拍照上传,互批纠错。
巩固练习
例4.如图,MF⊥NF于F,MF交AB于点E,NF交CD于点G∠1=140°,∠2=50°,试判断AB和CD的位置关系,并说明由.
解:过点F向左作FQ,使∠MFQ=∠2=50°,
则∠NFQ=∠MFN-∠MFQ=90°-50°=40°,所以AB∥FQ.
又因为∠1=140°,
所以∠1+∠NFQ=180°,
所以CD∥FQ,所以AB∥CD.
Q
要求:学生独立完成学案“课上学习”部分4题,
小组讨论,选一份拍照上传,对比分析。
自学释疑、拓展提升
知识点二:?在同一平面内,垂直于同一条直线的两条直线平行
自学问题:学案练习4解题方案单一。
学生典型问题展示:学案练习4存在问题图片展示.
解决方式:教师问题引导,学生组内或组间讨论,以小组为单位展示. 同学或教师
及时评价展示过程中暴露的问题.
自主检测
在同一平面内,b⊥a,c⊥a,试说明:b∥c.
a
b
c
1
2
∵b⊥a ,c ⊥a (已知)
∴b∥c
(同位角相等,两直线平行)
∴∠1= ∠2 = 90°
(垂直的定义)
解法1:如图,
自主检测
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(内错角相等,两直线平行)
a
b
c
1
2
解法2:如图,
在同一平面内,b⊥a,c⊥a,试说明:b∥c.
同一平面内,垂直于同一条直线
的两条直线平行.
几何语言:
∵ b⊥a,c⊥a(已知)
∴b∥c(同一平面内,垂直于同一条直线的两条
直线平行.)
a
b
c
1
2
归纳总结
巩固练习
例4 如图,为了说明示意图中的平安大街与长安街是互相平行的,在地图上量得∠1=90°,你能通过 度量图中已标出的其他的角来
验证这个结论吗? 说出你的理由.
解:方法1:测出∠3=90°,
理由是同位角相等,两直线平行.
方法2:测出∠2=90°,
理由是同旁内角互补,两直线平行.
方法3:测出∠5=90°,
理由是内错角相等,两直线平行.
方法4:测出∠2,∠3,∠4,∠5中任意一个角为90°,
理由是同一平面内,垂直于同一直线的两直线平行.
课堂总结
1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.平行于同一直线的两直线平行.
5.同一平面内, 垂直于同一直线的两直线平行.
6.平行线的定义.
判定两条直线是否平行的方法有:
1
2
3
积
分
榜
课堂总结
平行线判定方法的综合运用
自主学习反馈
完成率反馈,表扬优秀学生;由平台数据,找到共性和个性问题。
表扬:课前检测正确率高的学生:图片展示
学案书写工整的学生:图片展示(主要是学案上主观题书写规范展示)
课前检测和学案整体完成情况较好的学生:图片展示(课前自主学习整体完成优秀展示)
问题:共性典型问题:图片展示(课前自主学习中两个或者至多三个典型共性问题的展示)
个性典型问题:图片展示(课前自主学习中两个或者至多三个典型个性问题的展示)
学习目标
1.进一步掌握平行线的判定方法,并会运用平行线的
判定解决问题;(重点)
2.掌握垂直于同一条直线的两条直线互相平行.
自学释疑、拓展提升
知识点一:?平行线的判定的综合运用
自学问题:不能准确的选择平行线判定方法,书写不规范
学生典型问题展示:(学生课前问题图片展示)错误率较高习题和学案练习题。
解决方式:教师问题引导,学生组内或组间讨论,以小组为单位展示. 同学或教师
及时评价展示过程中暴露的问题.
(3)如果∠D+∠DFE=180°,可以判断哪两条直线平行?为什么?
例1 如图,E是AB上一点,F是DC上一点,G是BC延长线上一点.
(1)如果∠B=∠DCG,可以判断哪两条直线平行?为什么?
(2)如果∠D=∠DCG,可以判断哪两条直线平行? 为什么?
A
B
D
C
E
F
G
解 (1)AB//CD, 同位角相等,两直线平行;
(2)AD//BC, 内错角相等,两直线平行;
(3)AD//EF, 同旁内角互补,两直线平行.
活动形式:抢答,前三名同学到讲台讲解,其他学生聆听纠错。
巩固练习
例2:如图,已知 ∠1=75o , ∠2 =105o问:AB与CD平行吗?为什么?
A
C
1
4
2
3
B
D
5
F
E
75o
105o
还有其它解法吗?
巩固练习
例2:如图,已知 ∠1=75o , ∠2 =105o问:AB与CD平行吗?为什么?
A
C
1
4
2
3
B
D
5
F
E
75o
105o
巩固练习
例3 如图,∠1=∠2,能判断AB∥DF吗?为什么?
?
?
?
?
?
?
F
D
C
A
B
E
1
2
解:不能.
添加∠CBD=∠EDB
内错角相等,两直线平行
若不能判断AB∥DF,你认为还需要再添加的一个条件是什么呢?写出这个条件,并说明你的理由.
巩固练习
要求:学生独立完成学案“课上学习”部分3题,拍照上传,互批纠错。
巩固练习
例4.如图,MF⊥NF于F,MF交AB于点E,NF交CD于点G∠1=140°,∠2=50°,试判断AB和CD的位置关系,并说明由.
解:过点F向左作FQ,使∠MFQ=∠2=50°,
则∠NFQ=∠MFN-∠MFQ=90°-50°=40°,所以AB∥FQ.
又因为∠1=140°,
所以∠1+∠NFQ=180°,
所以CD∥FQ,所以AB∥CD.
Q
要求:学生独立完成学案“课上学习”部分4题,
小组讨论,选一份拍照上传,对比分析。
自学释疑、拓展提升
知识点二:?在同一平面内,垂直于同一条直线的两条直线平行
自学问题:学案练习4解题方案单一。
学生典型问题展示:学案练习4存在问题图片展示.
解决方式:教师问题引导,学生组内或组间讨论,以小组为单位展示. 同学或教师
及时评价展示过程中暴露的问题.
自主检测
在同一平面内,b⊥a,c⊥a,试说明:b∥c.
a
b
c
1
2
∵b⊥a ,c ⊥a (已知)
∴b∥c
(同位角相等,两直线平行)
∴∠1= ∠2 = 90°
(垂直的定义)
解法1:如图,
自主检测
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(内错角相等,两直线平行)
a
b
c
1
2
解法2:如图,
在同一平面内,b⊥a,c⊥a,试说明:b∥c.
同一平面内,垂直于同一条直线
的两条直线平行.
几何语言:
∵ b⊥a,c⊥a(已知)
∴b∥c(同一平面内,垂直于同一条直线的两条
直线平行.)
a
b
c
1
2
归纳总结
巩固练习
例4 如图,为了说明示意图中的平安大街与长安街是互相平行的,在地图上量得∠1=90°,你能通过 度量图中已标出的其他的角来
验证这个结论吗? 说出你的理由.
解:方法1:测出∠3=90°,
理由是同位角相等,两直线平行.
方法2:测出∠2=90°,
理由是同旁内角互补,两直线平行.
方法3:测出∠5=90°,
理由是内错角相等,两直线平行.
方法4:测出∠2,∠3,∠4,∠5中任意一个角为90°,
理由是同一平面内,垂直于同一直线的两直线平行.
课堂总结
1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.平行于同一直线的两直线平行.
5.同一平面内, 垂直于同一直线的两直线平行.
6.平行线的定义.
判定两条直线是否平行的方法有:
1
2
3
积
分
榜
课堂总结
