2020-2021学年华师版八年级下册16.2.1分式的乘除(共15张)
文档属性
| 名称 | 2020-2021学年华师版八年级下册16.2.1分式的乘除(共15张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-26 17:20:55 | ||
图片预览




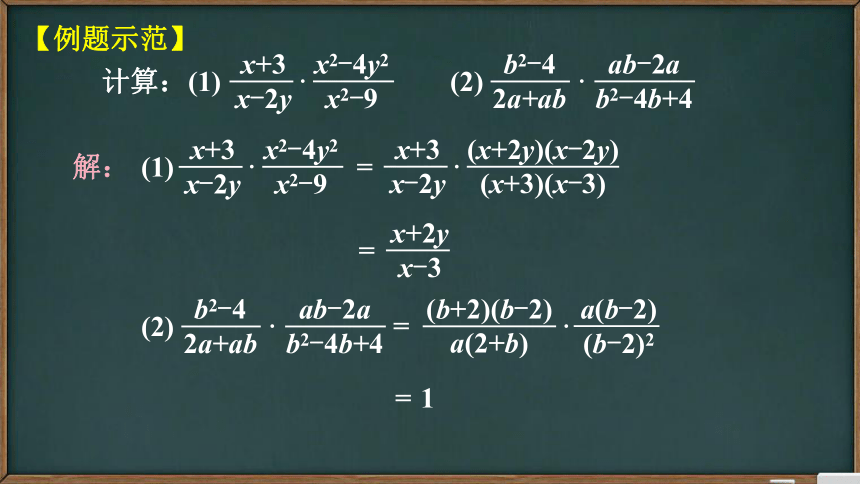


文档简介
华东师大版数学八年级下册
第16章 《分式》
16.2.1 分式的乘除
学而不思则罔,疑而不探则空
【学习目标】
1、经历探索分式的乘除、乘方运算的过程,
通过与分数相应运算的类比,发展联想
能力和合情推理能力;
2、能进行简单分式的乘除、乘方运算;
3、在分式除法运算转化为乘法运算的过程中,
进一步体验转化思想在数学中的应用。
【类比探索】
分数的乘法:
分数乘分数,用分子的积作为积的分子,分母的积作为积的分母,如果得到的不是最简分数,应该通过约分进行化简。
即
(b、d均不为0)
如:
3×10
5×21
=
a·c
b·d
=
cd
ab
·
35
×
10
21
2
7
=
35
×
15
3×15
5
=
9
=
37
×
0.4
=
37
×
2
5
3×2
7×5
=
6
35
=
【类比归纳】
一、分式的乘法:
分式乘分式,用分子的积作为积的分子,分母的积作为积的分母. 如果得到的不是最简分式,通过约分化简。
即
A·C
B·D
=
(A、B、C、D是整式且B≠0,C≠0)
如:
a2x·ay2
by2·b2x
CD
AB
·
=
a2x
by2
ay2
b2x
·
=
a3
b3
如果分子、分母是能分解因式的多项式呢?
-4a4b2
15x2
9x
8a4b
·
=
4a4b2·9x
15x2·8a4b
-
3b
10x
-
=
计算:(1)
【例题示范】
解:
x+3
x-2y
·
x2-4y2
x2-9
b2-4
2a+ab
·
ab-2a
b2-4b+4
(2)
(1)
x+3
x-2y
·
x2-4y2
x2-9
=
x+3
x-2y
·
(x+2y)(x-2y)
(x+3)(x-3)
=
x+2yx-3
b2-4
2a+ab
·
ab-2a
b2-4b+4
(2)
(b+2)(b-2)
a(2+b)
·
a(b-2)
(b-2)2
=
=
1
【类比探索】
分数的除法:
一个数除以分数,相当于这个数乘以分数的倒数.
即
(b、c、d均不为0)
如:
cd
ab
÷
35
÷
9
10
2
3
=
35
÷
15
5
3
=15×
25
=
37
÷
0.6
=
35
×
73
7
5
=
d
c
ab
·
=
乘积为1的两个数互为倒数. 0没有倒数.
35
×
109
=
【类比归纳】
二、分式的除法:
分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘。
即
=
(B≠0,C≠0,D≠0)
如:
CD
AB
÷
=
x3
z3
-4a4b2
15x2
-8a4b
9x
÷
=
3b
10x
DC
AB
·
=
a2xy
b2z2
b2x2a2yz
·
a2xy
b2z2
a2yz
b2x2
÷
=
-4a4b2
15x2
9x
-8a4b
·
计算:
【例题示范】
解:
÷
a
a-2
(2) (a2-2a)
ab(a+b)
a-b
(3) (a3b-ab3)÷(a+b)·
m-1
m2-6m+9
÷
m2-1
m2-9
(1)
原式=
(m+3)(m-3)
(m+1)(m-1)
·
m-1
(m-3)2
m+3
(m+1)(m-3)
=
解:
原式=
a-2
a
a(a-2)
·
=(a-2)2
=a2-4a+4
解:
原式=
ab(a+b)
a-b
ab(a-b)· ·
1
a+b
=a2b2
分式乘除运算的结果是最简分式或整式。
【探索交流】
Q:根据乘方的意义及分式的乘法, 如何进行分式的乘方呢?
如计算:
25
(1) ( )3
分数的乘方,将分子、分母分别乘方.
ba
(2) ( )3
ba
(3) ( )n ( n为整数, 且n≥2)
解:
25
(1) ( )3
23
53
=
8
125
=
ba
(2) ( )3
=
ba
·
ba
·
ba
b·b·b
a·a·a
=
b3
a3
=
ba
(3) ( )n
=
ba
·
ba
·
ba
·
···
b·b·····b
a·a·····a
=
n个
n个
n个
bn
an
=
【知识归纳】
三、分式的乘方:
分式的乘方,将分子、分母分别乘方。
即
=
(B≠0,n为大等于2的整数)
如:
AnBn
AB
( )n
y
-2x
( )2
y2
(-2x)2
=
y2
4x2
=
-2a
c2
( )3
(-2a)3
(c2)3
=
8a3
c6
=-
a2-a-2
a3(2-a)
[ ]2
=
(a+1)(a-2)
-a3(a-2)
[ ]2
(a+1)2
(-a3)2
=
(a+1)2
a6
=
【综合练习】
1、计算:
(1)
÷
x2
y
(- )2
·
y2
x
(- )3
y
x
(- )4
ab
a-b
( )2
·
(2ab-a2-b2)
(a-b)3
ab
÷
(2)
解:
原式=
x4
y2
·
y6
x3
(- )
x4
y4
·
=-x5
解:
原式=
(ab)2
(a-b)2
·
(a-b)3
ab
-1
(a-b)2
·
ab
a-b
=-
ab
b-a
(或)=
分式的乘方与乘除混合时,应先算乘方,再算乘除,有多项式时,要先分解因式,再约分。
【综合练习】
2、已知x=-2,求 的值.
解:
原式=
2-2x
x
(- ) ÷(x3+2x2-3)÷(- )
3
1-x
x
2
8(x-1)3
x3
1
x(x+3)(x-1)
·
x2
(x-1)2
·
8
x2(x+3)
=
当x=-2时,
8
x2(x+3)
=
8
(-2)2·(-2+3)
=2
课堂小结:
1、分式的乘除法与分数的乘除法类似,分式的乘除法
都统一成乘法,分式乘除法的实质是分式的约分,
而分式的约分的讨论依据是分式的基本性质;
2、分式乘除法的运算按从左到右的顺序进行计算,
结果不是最简分式的,要进行约分;
3、在有乘方和乘除运算时,先确定运算中乘方结果的
符号,负数奇次方为负,偶次方为正。还要注意运
算顺序,先算乘方,后算乘除。
【课后练习】
1、课本P8练习题.(做在书上,同组互查)
2、课本P10习题16.2的1、5题.
(做在作业本上,午自习后交)
【课后拓展】
3、从甲地到乙地有两条路。每条路都是3km,其中第一条
是平路,第二条有1km的上坡路,2km的下坡路,小明
在上坡路上的骑车速度为akm/h,在平路上的骑车速度
为2akm/h,在下坡路上的骑车速度为3akm/h。那么
(1) 当他分别走第一条路和第二条路时,从甲地到乙地
各需多长时间? (2) 从甲地到乙地他走哪条路花费的
时间少?少用多长时间?
1、计算:
a2÷b· ÷c· ÷d·
1b
1c
1d
2、先化简, 再求值: ,其中a2-a=0.
÷
a2-4
a2-2a+1
·
a-1
a+2
1
a2-1
第16章 《分式》
16.2.1 分式的乘除
学而不思则罔,疑而不探则空
【学习目标】
1、经历探索分式的乘除、乘方运算的过程,
通过与分数相应运算的类比,发展联想
能力和合情推理能力;
2、能进行简单分式的乘除、乘方运算;
3、在分式除法运算转化为乘法运算的过程中,
进一步体验转化思想在数学中的应用。
【类比探索】
分数的乘法:
分数乘分数,用分子的积作为积的分子,分母的积作为积的分母,如果得到的不是最简分数,应该通过约分进行化简。
即
(b、d均不为0)
如:
3×10
5×21
=
a·c
b·d
=
cd
ab
·
35
×
10
21
2
7
=
35
×
15
3×15
5
=
9
=
37
×
0.4
=
37
×
2
5
3×2
7×5
=
6
35
=
【类比归纳】
一、分式的乘法:
分式乘分式,用分子的积作为积的分子,分母的积作为积的分母. 如果得到的不是最简分式,通过约分化简。
即
A·C
B·D
=
(A、B、C、D是整式且B≠0,C≠0)
如:
a2x·ay2
by2·b2x
CD
AB
·
=
a2x
by2
ay2
b2x
·
=
a3
b3
如果分子、分母是能分解因式的多项式呢?
-4a4b2
15x2
9x
8a4b
·
=
4a4b2·9x
15x2·8a4b
-
3b
10x
-
=
计算:(1)
【例题示范】
解:
x+3
x-2y
·
x2-4y2
x2-9
b2-4
2a+ab
·
ab-2a
b2-4b+4
(2)
(1)
x+3
x-2y
·
x2-4y2
x2-9
=
x+3
x-2y
·
(x+2y)(x-2y)
(x+3)(x-3)
=
x+2yx-3
b2-4
2a+ab
·
ab-2a
b2-4b+4
(2)
(b+2)(b-2)
a(2+b)
·
a(b-2)
(b-2)2
=
=
1
【类比探索】
分数的除法:
一个数除以分数,相当于这个数乘以分数的倒数.
即
(b、c、d均不为0)
如:
cd
ab
÷
35
÷
9
10
2
3
=
35
÷
15
5
3
=15×
25
=
37
÷
0.6
=
35
×
73
7
5
=
d
c
ab
·
=
乘积为1的两个数互为倒数. 0没有倒数.
35
×
109
=
【类比归纳】
二、分式的除法:
分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘。
即
=
(B≠0,C≠0,D≠0)
如:
CD
AB
÷
=
x3
z3
-4a4b2
15x2
-8a4b
9x
÷
=
3b
10x
DC
AB
·
=
a2xy
b2z2
b2x2a2yz
·
a2xy
b2z2
a2yz
b2x2
÷
=
-4a4b2
15x2
9x
-8a4b
·
计算:
【例题示范】
解:
÷
a
a-2
(2) (a2-2a)
ab(a+b)
a-b
(3) (a3b-ab3)÷(a+b)·
m-1
m2-6m+9
÷
m2-1
m2-9
(1)
原式=
(m+3)(m-3)
(m+1)(m-1)
·
m-1
(m-3)2
m+3
(m+1)(m-3)
=
解:
原式=
a-2
a
a(a-2)
·
=(a-2)2
=a2-4a+4
解:
原式=
ab(a+b)
a-b
ab(a-b)· ·
1
a+b
=a2b2
分式乘除运算的结果是最简分式或整式。
【探索交流】
Q:根据乘方的意义及分式的乘法, 如何进行分式的乘方呢?
如计算:
25
(1) ( )3
分数的乘方,将分子、分母分别乘方.
ba
(2) ( )3
ba
(3) ( )n ( n为整数, 且n≥2)
解:
25
(1) ( )3
23
53
=
8
125
=
ba
(2) ( )3
=
ba
·
ba
·
ba
b·b·b
a·a·a
=
b3
a3
=
ba
(3) ( )n
=
ba
·
ba
·
ba
·
···
b·b·····b
a·a·····a
=
n个
n个
n个
bn
an
=
【知识归纳】
三、分式的乘方:
分式的乘方,将分子、分母分别乘方。
即
=
(B≠0,n为大等于2的整数)
如:
AnBn
AB
( )n
y
-2x
( )2
y2
(-2x)2
=
y2
4x2
=
-2a
c2
( )3
(-2a)3
(c2)3
=
8a3
c6
=-
a2-a-2
a3(2-a)
[ ]2
=
(a+1)(a-2)
-a3(a-2)
[ ]2
(a+1)2
(-a3)2
=
(a+1)2
a6
=
【综合练习】
1、计算:
(1)
÷
x2
y
(- )2
·
y2
x
(- )3
y
x
(- )4
ab
a-b
( )2
·
(2ab-a2-b2)
(a-b)3
ab
÷
(2)
解:
原式=
x4
y2
·
y6
x3
(- )
x4
y4
·
=-x5
解:
原式=
(ab)2
(a-b)2
·
(a-b)3
ab
-1
(a-b)2
·
ab
a-b
=-
ab
b-a
(或)=
分式的乘方与乘除混合时,应先算乘方,再算乘除,有多项式时,要先分解因式,再约分。
【综合练习】
2、已知x=-2,求 的值.
解:
原式=
2-2x
x
(- ) ÷(x3+2x2-3)÷(- )
3
1-x
x
2
8(x-1)3
x3
1
x(x+3)(x-1)
·
x2
(x-1)2
·
8
x2(x+3)
=
当x=-2时,
8
x2(x+3)
=
8
(-2)2·(-2+3)
=2
课堂小结:
1、分式的乘除法与分数的乘除法类似,分式的乘除法
都统一成乘法,分式乘除法的实质是分式的约分,
而分式的约分的讨论依据是分式的基本性质;
2、分式乘除法的运算按从左到右的顺序进行计算,
结果不是最简分式的,要进行约分;
3、在有乘方和乘除运算时,先确定运算中乘方结果的
符号,负数奇次方为负,偶次方为正。还要注意运
算顺序,先算乘方,后算乘除。
【课后练习】
1、课本P8练习题.(做在书上,同组互查)
2、课本P10习题16.2的1、5题.
(做在作业本上,午自习后交)
【课后拓展】
3、从甲地到乙地有两条路。每条路都是3km,其中第一条
是平路,第二条有1km的上坡路,2km的下坡路,小明
在上坡路上的骑车速度为akm/h,在平路上的骑车速度
为2akm/h,在下坡路上的骑车速度为3akm/h。那么
(1) 当他分别走第一条路和第二条路时,从甲地到乙地
各需多长时间? (2) 从甲地到乙地他走哪条路花费的
时间少?少用多长时间?
1、计算:
a2÷b· ÷c· ÷d·
1b
1c
1d
2、先化简, 再求值: ,其中a2-a=0.
÷
a2-4
a2-2a+1
·
a-1
a+2
1
a2-1
