第1章 特殊四边形同步练习

《1.1平行四边形及其性质(1)》课时训练
1．中，则和的度数分别为（ ）．
A．， B．， C．， D．，
2．已知平行四边形的周长为，相邻两边的比为1：2，则较短的边长为（ ）．
A． B． C． D．
3.在ABCD中，∠A∶∠B∶∠C∶∠D的值可以是（ ）
A.1∶2∶3∶4 B.1∶2∶2∶1
C.1∶1∶2∶2 D.2∶1∶2∶1
4．如图，在ABCD中，已知AD＝8㎝， AB＝6㎝， DE平分∠ADC交BC边于点E，则BE等于
5如图，ABCD中，、分别为、边上的点，要使需添加一个条件： ．
6.如图，小明用一根36m长的绳子围成了一个平行四边形的场地，其中一条边AB长为8m，其他三条边各长多少？
　　　　　　　　　　　　　　　　　　
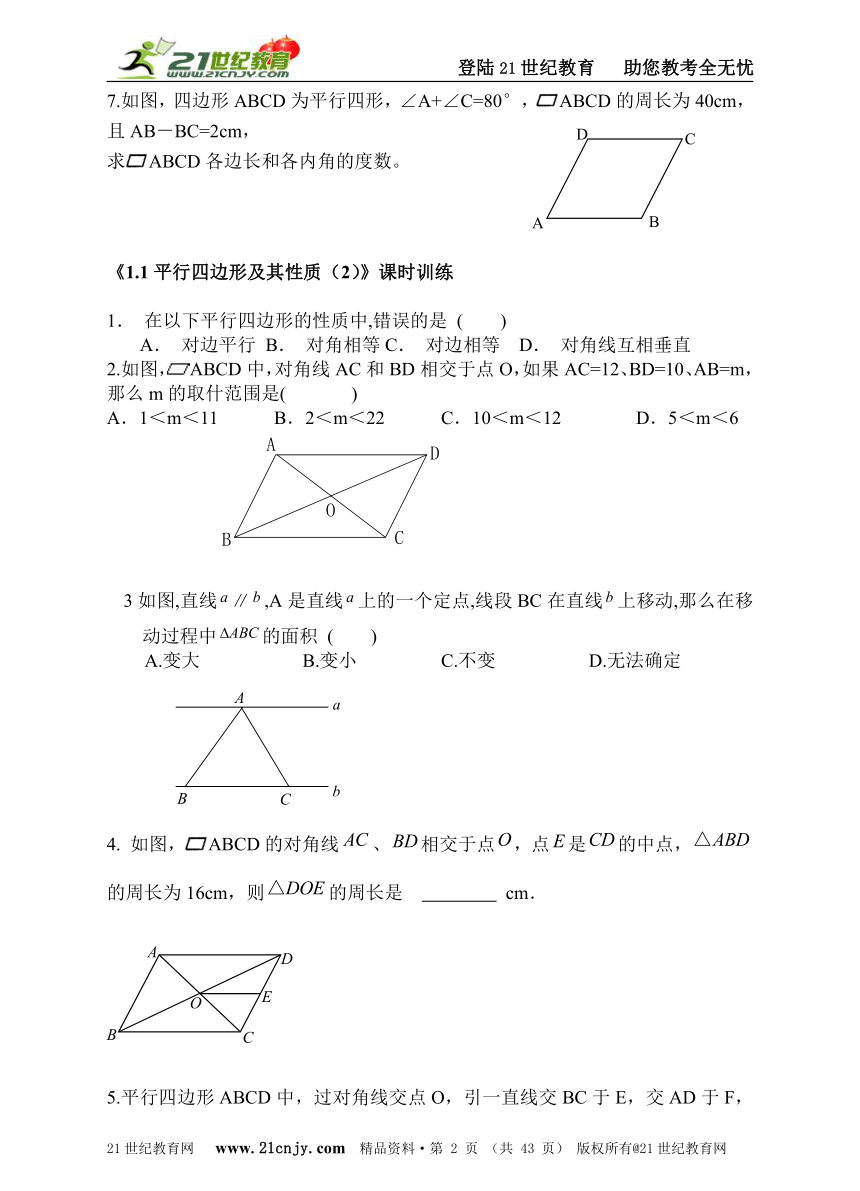
7.如图，四边形ABCD为平行四形，∠A+∠C=80°，ABCD的周长为40cm，且AB－BC=2cm，
求ABCD各边长和各内角的度数。
《1.1平行四边形及其性质（2）》课时训练
1． 在以下平行四边形的性质中,错误的是 ( )
A． 对边平行 B． 对角相等C． 对边相等 D． 对角线互相垂直
2.如图，ABCD中，对角线AC和BD相交于点O，如果AC=12、BD=10、AB=m，那么m的取什范围是( )
A．1＜m＜11 B．2＜m＜22 C．10＜m＜12 D．5＜m＜6
3如图,直线∥,A是直线上的一个定点,线段BC在直线上移动,那么在移动过程中的面积 ( )
A.变大 B.变小 C.不变 D.无法确定


4. 如图，ABCD的对角线、相交于点，点是的中点，的周长为16cm，则的周长是 cm．
5.平行四边形ABCD中，过对角线交点O，引一直线交BC于E，交AD于F，若AB=2.4cm，BC=4cm，OE=1.1cm，则四边形CDFE周长为________．
6.平行四边形周长等于68cm，被两条对角线分成两个不同的三角形的周长和等于80cm，两对角线的长度之比是2∶3，求两条对角线的长度．

《1.2平行四边形的判定》课时训练
1．不能判定四边形ABCD为平行四边形的题设是（ ）
（A）AB=CD，AD=BC （B）ABCD
（C）AB=CD，AD∥BC （D）AB∥CD，AD∥BC
2．下列说法正确的是（ ）
A．若一个四边形的一条对角线平分另一条对角线，则这个四边形是平行四边形
B．对角线互相平分的四边形一定是平行四边形
C．一组对边相等的四边形是平行四边形
D．有两个角相等的四边形是平行四边形
3．四边形ABCD，从（1）AB∥CD；（2）AB=CD；（3）BC∥AD；（4）BC=AD这四个条件中任选两个，其中能使四边形ABCD是平行四边形的选法有（ ）
A．3种 B．4种 C．5种 D．6种
4．四边形的四条边长分别是a，b，c，d，其中a，b为一组对边边长，c，d为另一组对边边长且满足a2+b2+c2+d2=2ab+2cd，则这个四边形是（ ）
A．任意四边形 B．平行四边形
C．对角线相等的四边形 D．对角线垂直的四边形
5．如图所示，AO=OC，BD=16cm，则当OB=_____cm时，四边形ABCD是平行四边形．
6．如图所示，在ABCD中，E，F是对角线AC上的两点，且AF=CE，则线段DE与BF的长度相等吗？

平行四边形的性质与判定(45分钟基础测试+能力测试题)
一.选择题(每小题4分,共24分)
1.以三角形的三个顶点及三边中点为顶点的平行四边形共有：（ ）
（A）1个 （B）2个 （C）3个 （D）4个
2．能判定四边形ABCD为平行四边形的题设是（ ）．
（A）AB∥CD，AD=BC; （B）∠A=∠B，∠C=∠D;
（C）AB=CD，AD=BC; （D）AB=AD，CB=CD
3．在给定的条件中，能画出平行四边形的是（ ）．
（A）以60cm为一条对角线，20cm、34cm为两条邻边;
（B）以6cm、10cm为对角线，8cm为一边;
（C）以20cm、36cm为对角线，22cm为一边;
（D）以6cm为一条对角线，3cm、10cm为两条邻边
4．在平行四边形ABCD中，AC与BD交于O，则其中共有（ ）对全等的三角形．
（A）1 （B）2
（C）3 （D）4
5．如图，ABCD中，AC．BD为对角线，BC＝6，BC边上的高为4，则阴影部分的面积为（ ）．
A．3 B．6 C．12 D．24
6．在平行四边形ABCD中，点A1、A2、A3、A4和C1、C2、C3、C4分别AB和CD的五等分点,点B1、B2和D1、D2分别是BC和DA的三等分点,已知四边形A4 B2 C4 D2的积为1,则平行四边形ABCD面积为（）
A.2 B. C. D.15
二.填空题(每小题5分,共20分)

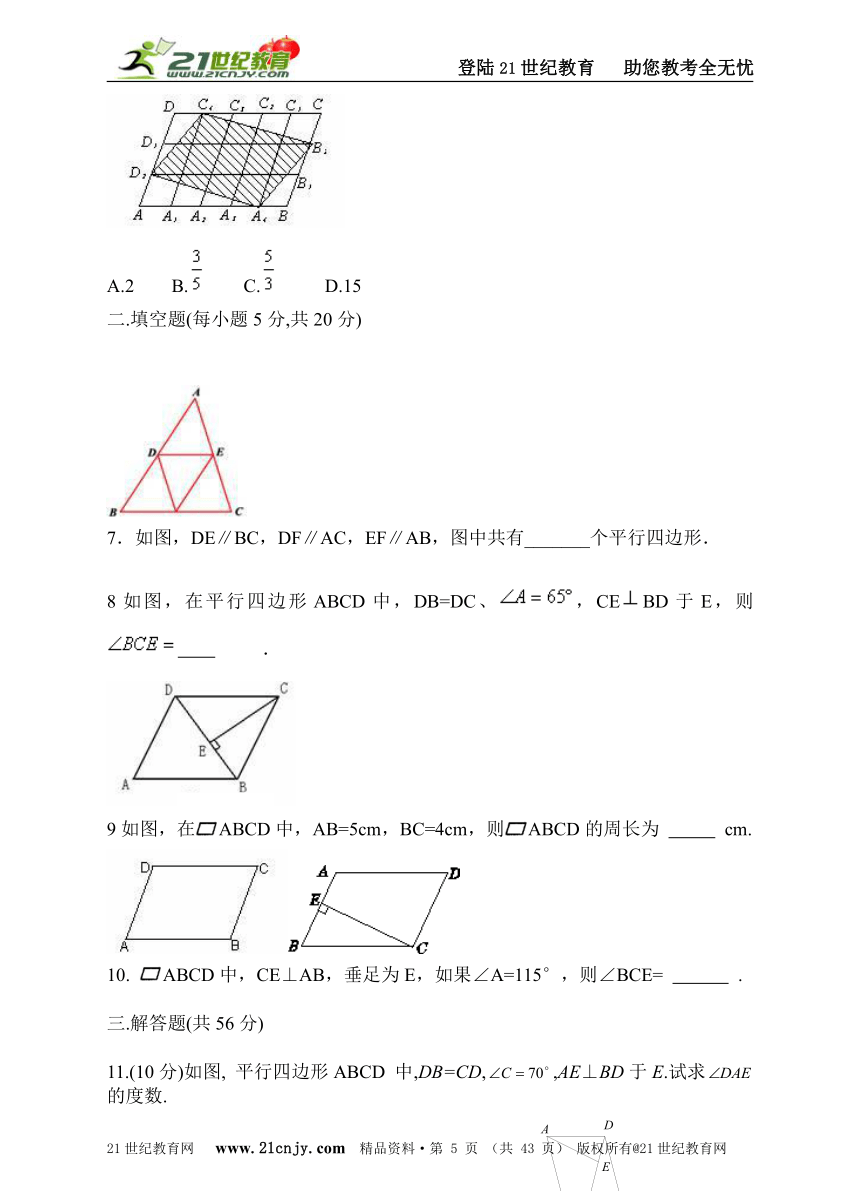
7．如图，DE∥BC，DF∥AC，EF∥AB，图中共有_______个平行四边形．
8如图，在平行四边形ABCD中，DB=DC、，CEBD于E，则 ．
9如图，在ABCD中，AB=5cm，BC=4cm，则ABCD的周长为 cm.
10. ABCD中，CE⊥AB，垂足为E，如果∠A=115°，则∠BCE= .
三.解答题(共56分)
11.(10分)如图, 平行四边形ABCD 中,DB=CD,,AE⊥BD于E.试求的度数.
12. (10分)李大伯家有一口如图所示的四边形的池塘,在它的四个角上均有一棵大柳树,李大伯开挖池塘,使池塘面积扩大一倍,又想保持柳树不动,如果要求新池塘成平行四边形的形状.请问李大伯愿望能否实现?若能,请画出你的设计;若不能,请说明理由.


13 .(12分)如图，平行四边形中，，，．对角线相交于点，将直线绕点顺时针旋转，分别交于点．
（1）证明：当旋转角为时，四边形是平行四边形；
（2）试说明在旋转过程中，线段与总保持相等；
14(12分)如图，是平行四边形的对角线上的点，． 请你猜想：与有怎样的位置关系和数量关系？并对你的猜想加以证明．
猜想：
15. (12分)如图，在中，，，将绕点沿逆时针方向旋转得到．
（1）线段的长是 ，
的度数是 ；
（2）连结，求证：四边形是平行四边形；
（3）求四边形的面积．
能力测试题
1．如图，在平行四边形ABCD中，M、N分别是AB、CD的中点，BD分别交AN、CM于点P、Q，在结论：
①DP=PQ=QB ②AP=CQ ③CQ=2MQ ④S△ADP=SABCD中，正确的个数为（ ）．
（A）1 （B）2 （C）3 （D）4

2.已知四边形ABCD中,AC交BD于点O,如果只给条件“AB∥CD”,那么还不能判定四边形ABCD为平行四边形,给出以下四种说法:
(1)如果再加上条件“BC=AD”,那么四边形ABCD一定是平行四边形;
(2)如果再加上条件“”,那么四边形ABCD一定是平行四边形;
(3)如果再加上条件“AO=OC”,那么四边形ABCD一定是平行四边形;
(4)如果再加上条件“”,那么四边形ABCD一定是平行四边形其中正确的说法是 ( )
A.(1)(2) B.(1)(3)(4) C.(2)(3) D.(2)(3)(4)
3．在ABCD中，点E，F分别是线段AD，BC上的两动点，点E从点A向D运动，点F从C向B运动，点E的速度m与点F的速度n满足_______关系时，四边形BFDE为平行四边形．
4．已知：如图，、是□的对角线上的两点，．
求证：（1）；（2）∥．
5（一题多解题）如图所示，在ABCD中，点E，F都在对角线AC上，且AE=CF，连结DE，BE，DF，BF，则四边形DEBF是平行四边形吗？为什么？
6．如图所示，在四边形ABCD中，AD∥BC，且AD>BC，BC=6cm，P，Q分别是线段AD，BC上两动点，P，Q分别从A，C出发，P以1cm/s的速度由A向D运动，Q以2cm/s的速度由C向B运动，P，Q两点同时开始运动，且开始运动的时刻是0．P，Q运动到顶点处即停止运动，问：第几秒时，四边形ABQP
是平行四边形？
《1.3特殊的平行四边形 矩形》课时训练
1．如图，矩形ABCD沿AE折叠．使D点落在BC边上的F点处．若∠BAF=58°．则∠DAE等于( 　　)
A．29° B. 32° C．16° D. 11°
2．矩形具有而一般平行四边形不具有的性质是(　)
A. 对角相等 B. 对边相等　　 C. 对角线相等 D. 对角线互相平分 3.如果一个矩形较短的边长为5cm．两条对角线所夹的角为60°，则这个矩形的面积是____cm2.
4. 如图所示，在矩形ABCD中，F是BC边上一点，AF的延长线交DC的延长线于G，DE⊥AG于E，且DE=DC，请不添辅助线在图中找出一对全等三角形，并证明之．
5. ．如图所示，在矩形ABCD中，对角线AC，BD交于点O，过顶点C作CE∥BD，交AB延长线于点E，求证：AC=CE．
6．如图，将矩形纸片沿对角线BD折叠，使点C落在C’处，BC’交AD于E，若∠EBD＝20°，求∠C’DE的度数。
7．如图，MN∥PQ，同旁内角的平分线AB、CB和AD、CD分别交于点B、D
⑴猜想AC和BD的位置关系是 。
⑵证明你的猜想。
《1.3特殊的平行四边形 菱形》课时训练
1.如图，下列条件之一能使平行四边形ABCD是菱形的为（ ）
① ② ③ ④
A．①③ B．②③ C．③④ D．①②③
2. 如图，菱形中，，对角线，则菱形的周长等于 ．
3.如图，菱形ABCD的对角线AC、BD交于点O，且AC＝16cm，BD＝12cm，求菱形ABCD的高为 cm。
4. 菱形ABCD的周长为20cm，两条对角线的比为3∶4，求菱形的面积。
5. 已知：如图，在ABCD中，AE平分∠BAD，与BC相交于点E，EF∥AB，与AD相交于点F，求证：四边形ABEF是菱形．
6. 已知:如图,菱形ABCD中, E，F分别是CB，CD上的点，且BE=DF.
(1)求证:AE=AF.
(2)若∠B=60°,点E，F分别为BC和CD的中点，求证:△AEF为等边三角形.
《1.3特殊的平行四边形 正方形》课时训练
1．如图，四边形ABCD是正方形，延长BC至点E，使CE=CA，连结AE交CD于点F，则∠AFC的度数是（ ）．
（A）150° （B）125° （C）135° （D）112．5°
2．小许拿了一张正方形的纸片如图甲，沿虚线对折一次得图乙．再对折一次得图丙．然后用剪刀沿图丙中的虚线（虚线与底边平行）剪去一个角．打开后的形状是（ ）．
3、周长为20cm的正方形,边长是 对角线长是 面积是

4、如图，有 个等腰直角三角形
5.如何设计花坛？在一块正方形的花坛上，欲修建两条直的小路，使得两条直的小路将花坛平均分成面积相等的四部分（不考虑道路的宽度），你有几种方法？（至少说出三种）
6.已知：在正方形ABCD中，E、F分别在BC、DC 上，且BE ＝ DF，AC与BC相交于O点，EF与AC相交于P点
求证：EF ⊥ AC，EF ∥ BD
《1.4特殊的平行四边形 图形的中心对称》课时训练
1．下列几何图形中，即是中心对称图形又是轴对称图形的是（ ）
A．正三角形 B．等腰直角三角形 C．等腰梯形 D．正方形
2．对右图的对称性表述，正确的是（ ）．
A．轴对称图形
B．中心对称图形
C．既是轴对称图形又是中心对称图形
D．既不是轴对称图形又不是中心对称图形
3．如图，△ABC的顶点坐标分别为A（4，6）、B（5，2）、C（2，1），如果将△ABC绕点C按逆时针方向旋转90°，得到△，那么点A的对应点的坐标是（ ）．
A．（－3，3） B．（3，－3） C．（－2，4） D．（1，4）
4.下列四个多边形：①等边三角形；②正方形；③正五边形；④正六边形．
其中，既是轴对称图形又是中心对称图形的是 .
5.如图，已知正方形的边长为3，
为边上一点， ．以点为中心，把△顺时
针旋转，得△，连接，则的长等于 ．
6.如图，在平面直角坐标系中，△ ABC的三个顶点的坐标分别为A（0,1），B（-1,1），C（-1,3）。
（1）画出△ABC关于x轴对称的△A1B1C1，并写出点C1的坐标；
（2）画出△ABC绕原点O顺时针方向旋转90°后得到的△A2B2C2，并写出点C2的坐标；，
（3）将△A2B2C2平移得到△ A3B3C3，使点A2的对应点是A3，点B2的对应点是B3
，点C2的对应点是C3（4，-1），在坐标系中画出△ A3B3C3，并写出点A3，B3的坐标。
特殊四边形与图形的中心对称 (45分钟基础测试+能力测试题)
一.选择题(每小题4分,共24分)
1. 1．下列说法中，不正确的是（ ）．
（A）有三个角是直角的四边形是矩形;（B）对角线相等的四边形是矩形
（C）对角线互相垂直的矩形是正方形;（D）对角线互相垂直的平行四边形是菱形
2．已知一个四边形的对角线互相垂直，那么顺次连接这个四边形的四边中点所得的四边形是（ ）．
（A）矩形 （B）菱形 （C）等腰梯形 （D）正方形
3．用两个全等的直角三角形拼下列图形：①矩形；②菱形；③正方形；④平行四边形；⑤等腰三角形；⑥等腰梯形．其中一定能拼成的图形是（ ）．
（A）①②③ （B）①④⑤ （C）①②⑤ （D）②⑤⑥
4．如图，将△ABC绕点C（0，-1）旋转180°得到△ABC，设点A的坐标为则点A的坐标为（ ）
（A） （B）
（C） （D）
5．矩形ABCD沿AE折叠，使点D落在BC边上的F点处，如果∠BAF=60°，那么∠DAE等于（ ）．
（A）15° （B）30° （C）45° （D）60°
6．在菱形ABCD中，∠ADC=120°，则BD：AC等于（ ）．
（A）：2 （B）：3 （C）1：2 （D）：1
二.填空题(每小题5分,共20分)
7.在平行四边形ABCD中，若添加一个条件________，则四边形ABCD是矩形；若添加一个条件_______，则四边形ABCD是菱形．
8．已知正方形的面积为4，则正方形的边长为________，对角线长为________．
9．已知矩形的对角线长为4cm，一条边长为2cm，则面积为________．
10．菱形的两条对角线分别是6cm，8cm，则菱形的边长为_____，面积为______．
三.解答题(共56分,)
11.（8分）如图，在菱形ABCD中，∠A与∠B的度数比为1：2，周长是48cm．求：
（1）两条对角线的长度；（2）菱形的面积．
12．（12分）已知：如图，平行四边形ABCD各角的平分线分别相交于点E，F，G，H，求证：四边形EFGH是矩形．

13．（12分）如图，适当地改变方格图中的平行四边形的部分位置，并保持面积不变，先使其成为矩形，再将矩形向下平移3个格后，继续改变其中某些部分的位置并保持面积不变，使其成为菱形．说明在变化过程中所运用的图形变换．
14．（12分）已知：如图，在正方形ABCD中，AE⊥BF，垂足为P，AE与CD交于点E，BF与AD交于点F，求证：AE=BF．
15．（12分）如图，要剪切如图①（尺寸单位：mm）所示的甲、乙两种直角梯形零件，且使两种零件的数量相等．有两种面积相等的矩形铝板，第一种长500mm，宽300mm（如图②）；第二种长600mm，宽250mm（如图③）可供选用．
（1）填空：为了充分利用材料，应选用第______种铝板，这时一块铝板最多能剪甲、乙两种零件共_______个，剪下这些零件后，剩余的边角料的面积是______mm2．
（2）画图：从图②或图③中选出待用的铝板示意图，在图上画出剪切线，并把边角余料用阴影表示出来．
能力测试
1. 两张能完全重合的等腰直角三角形纸片能拼成的图形是：①平行四边形（不包括菱形、矩形、正方形）②矩形（不包括正方形）③正方形④等边三角形⑤等腰直角三角形 ( )
A．①③⑤ B．②③⑤ C．①②③ D．①③④⑤
2. 四边形ABCD，仅从下列条件中任取两个加以组合，使得ABCD是平行四边形，一共有多少种不同的组合？（ ）
AB∥CD BC∥AD AB=CD BC=AD
（A）2组 （B）3组 （C）4组 （D）6组
3.现有一张长53cm，宽28cm的矩形纸片，要从中剪出长15cm，宽12cm的矩形小纸片，则最多能剪出______张．
4. 9．已知菱形ABCD的边长为6，∠A＝60°，如果点P是菱形内一点，且PB＝PD＝2那么AP的长为 ．
5. 如图，在四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA边上的中点，阅读下列材料，回答问题：
⑴连结AC、BD，由三角形中位线的性质定理可证四边形 EFGH是 。
⑵对角线AC、BD满足条件 时，四边形 EFGH是矩形。
⑶对角线AC、BD满足条件 时，四边形 EFGH是菱形。
⑷对角线AC、BD满足条件 时，四边形 EFGH是正方形。
6.如图，以△ABC的三边为边在BC的同侧分别作三个等边三角形，即△ABD、
△BCE、△ACF，请回答下列问题：
（1）四边形ADEF是什么四边形？并说明理由
（2）当△ABC满足什么条件时，四边形ADEF是菱形？
（3）当△ABC满足什么条件时，以A、D、E、F为顶点的四边形不存在．
《1.5特殊的平行四边形 梯形（1）》课时训练
1.等腰梯形ABCD中，E、F、G、H分别是各边的中点，则四边形EFGH的形状是（ ）
A．平行四边形 B．矩形 C．菱形 D．正方形
2. 等腰梯形上、下底差等于一腰的长，那么腰长与下底的夹角是（ ）.
A. 5° B. 60°
C.45° D.30°
3. 等腰梯形的高是腰长的一半，则底角为（ ）
A.30° B.45°
C.60° D.90°
4.梯形中，， ，，，，
则的长为 ．
5. 直角梯形的一腰长为10 cm，其与底边所成的角为45°，那么另一腰长为
6. 如图等腰梯形的底分别是3 cm和5 cm，一个角是45°，求等腰梯形的面积.
7如图，等腰梯形ABCD中，AB∥CD，DC＝AD＝BC，且对角线AC垂直于腰BC，求梯形的各个内角.
《1.5特殊的平行四边形 梯形（2）》课时训练
1. 下列命题中，真命题是（ ）.
A.有一组对边平行，另一组对边相等的梯形
B.有一组对边互补的梯形是等腰梯形
C.有一组邻角相等的四边形是等腰梯形
D. 有两组邻角分别相等的四边形是等腰梯形
2. 如图，在等腰梯形ABCD中AD=6cm，BD=9 cm，AB=8 cm，E、F、G、H分别是AD、BD、BC、AC的中点，那么四边形EFGH的周长是（ ）
A. 14cm B.15cm
C. 16cm D.17cm
3. 如图，等腰梯形ABCD，周长为40，∠BAD=60°，BD平分∠ABC，则CD的长为（ ）
4. 如图，在梯形ABCD中，AD∥BC，AC与BD相交于点O，且AC⊥BD，AC=4 cm，BD=3.5 cm，那么，梯形ABCD的面积为 .
5如图，梯形ABCD中，AB∥CD，AD＝BC，延长AB到E，使BE＝DC，连结AC、CE.求证：AC＝CE.
6如图所示，已知：直角梯形ABCD，AD∥BC，，AB＝8cm，AD＝24cm，BC＝26cm，有两个点P、Q分别从A、C出发各自沿AD和CB的方向运动，P点的速度是1cm∕s，Q点的速度为3cm∕s，当P、Q同时出发，多少秒后四边形PQCD是平行四边形或是等腰梯形？
《1.6特殊的平行四边形中位线定理》课时训练
1.三角形的三条中位线长分别为2cm、3cm、4cm，则原三角形的周长为（ ）．
（A）4．5cm （B）18cm （C）9cm （D）36cm
2.．如图,在△ABC中，E，D，F分别是AB，BC，CA的中点，AB=6，AC=4，则四边形AEDF的周长是（ ）
A．10 B．20 C．30 D．40
3. 三角形的三边长分别是3cm，5cm，6cm，则连结三边中点所围成的三角形的周长是_________cm
4．如图所示，A，B两点分别位于一个池塘的两端，小聪想用绳子测量A，B间的距离，但绳子不够长，一位同学帮他想了一个主意：先在地上取一个可以直接到达A，B的点C，找到AC，BC的中点D，E，并且测出DE的长为10m，则A，B间的距离为 。
A．15m B．25m C．30m D．20m
5. 如图所示，ABCD的对角线AC，BD相交于点O，AE=EB，求证：OE∥BC．
[来
6. 如图所示，已知在ABCD中，E，F分别是AD，BC的中点，求证：MN∥BC．
梯形与中位线定理(45分钟基础测试+能力测试题)
一.选择题(每小题4分,共24分)
1. . 如果梯形的面积是144 cm2，且两底之比为4∶5，高为16 cm，那么两底的长分别是（ ）
A.40 cm，10 cm B.6 cm，7.5 cm
C.8 cm，10 cm D.10 cm，12.5 cm
2. 在梯形ABCD中，AB∥CD，AB＞CD，如果∠D＞∠C，那么AD和BC的关系是（ ）
A. AD＞BC B. AD＝BC
C. AD＜BC D.不能确定
3等腰梯形两底之差的一半等于它的高，那么此梯形的一个底角是（ ）
A.30° B.45°
C.60° D.75°
4. 已知△ABC的周长为1，连结△ABC的三边中点构成第二个三角形，再连结第二个三角形的三边中点构成第三个三角形，依此类推，第2007个三角形的周长是（ ）
A．
5．如图所示，已知四边形ABCD，R，P分别是DC，BC上的点，E，F分别是AP，RP的中点，当点P在BC上从点B向点C移动而点R不动时， 那么下列结论成立的是（ ）
A．线段EF的长逐渐增大 B．线段EF的长逐渐减少
C．线段EF的长不变 D．线段EF的长不能确定
6．如图,在△ABC中，E，D，F分别是AB，BC，CA的中点，AB=6，AC=4，则四边形AEDF的周长是（ ）
A．10 B．20 C．30 D．40
二.填空题(每小题5分,共20分)
7. EF∥GH∥MN，AE=EG=GM=MB，GH=4，则EF=______，BC=________．
8. 如图，梯形ABCD中，AD∥BC，E、F分别是AD、BC的中点，若∠B＋∠C＝90°，AD＝7，BC＝15，则EF的长是 .
9. 已知梯形ABCD中，AD∥BC，∠ABC＝60°，BD＝，AE是梯形的高线，且BE＝1，则AD＝ .
10. 在Rt△ABC中，∠C=90°，AC=5，BC=12，则连结两条直角边中点的线段长为_______．
三.解答题(共56分,)
11.（10分）如图，等腰梯形ABCD中，AD∥BC，AD＝3，AB＝4，BC＝7，求∠B的度数.
12. （10分）如图，梯形ABCD中，AB∥CD，AD＝BC，延长AB到E，使BE＝DC，连结AC、CE.求证：AC＝CE.
13. （12分）已知：如图，平行四边形ABCD的对角线AC，BD相交于点O，AE=EB．求证：OE∥BC．
14. （12分）在梯形中，∥，，为中点．
（1）求证：≌．（2）若平分，且，求的长．

15. （12分）如图，方格纸中的每个小方格都是边长为1个单位的正方形，Rt△ABC的顶点均在个点上，在建立平面直角坐标系后，点A的坐标为（－6，1），点B的坐标为（－3，1），点C的坐标为（－3，3）．
（1）将Rt△ABC沿x轴正方向平移5个单位得到Rt△A1B1C1，试在图上画出的图形Rt△A1B1C1，并写出点A1的坐标；
（2）将原来的Rt△ABC绕点B顺时针旋转90°得到Rt△A2B2C2，试在图上画出Rt△A2B2C2的图形．

能力测试
1. 梯形ABCD中，AB∥CD，若AD=m，CD=n，AB=m+n，则下列等式一定成立的是（ ）．
A．∠A=∠B B．∠D=2∠B C．BC=m-n D．BC=m+n
2.如图，梯形ABCD中，AD∥BC，且AD：BC=3：5，梯形ABCD的面积是8cm2，点M、N分别是AD和BC上一点，E、F分别是BM、CM的中点，则四边形MENF的面积是_______cm2．
3. 如图，梯形ABCD中，AD∥BC，E、F分别是AD、BC的中点，若∠B＋∠C＝90°，AD＝7，BC＝15，则EF的长是 .
4. 如图，在△ABC中，已知AB=6，AC=10，AD平分∠BAC，BD⊥AD于点D，E为BC中点．DE= ．
5．已知：如图，矩形ABCD中，AC和BD交于点O，E、F分别是OA、OD的中点．求证：四边形EBCF是等腰梯形．
6.下面是某同学证一道几何题的过程：
题目：已知四边形ABCD中，AB＝DC，AC＝BD，AD≠BC，求证：四边形ABCD是等腰梯形（如图11）.
证明：过D作DE∥AB，交BC于点E.
则：∠ABE＝∠1 ·····①
∵AB＝DC，AC＝BD，BC＝CB
∴△ABC≌△DCB ····②
∴∠ABC＝∠DCB ····③
∴∠1＝∠DCB ····④
∴AB＝DC＝DE ····⑤
∴四边形ABCD是平行四边形
AD∥BC，BE＝AD ····⑥
又∵AD≠BC，∴E、C是不同的点，DC不平行于AB ····⑦
又∵AB＝CD，∴四边形ABCD是等腰梯形····⑧
读后填空：
（1）证明过程是否有错？如有，错在第几步，答： .
（2）作DE∥AB的目地是 .
（3）有人认为第⑦步是多余的，你认为是否多余？答： .
（4）判断四边形ABCD为平行四边形的依据是 .
（5）判断四边形ABCD为等腰梯形的依据是 .
（6）若题目中没有AD≠BC，那么四边形ABCD一定是等腰梯形吗？为什么？
特殊四边形（全章45分钟基础测试+能力测试题）
一.选择题(每小题4分,共24分)
1．下列说法错误的是（ ）．
A．对角线互相平分的四边形是平行四边形 B．对角线互相垂直的四边形是矩形
C．对角线相等的平行四边形是矩形 D．对角线互相垂直的矩形是正方形
2．矩形各内角平分线围成的四边形是（ ）．
A．平行四边形 B．矩形 C．菱形 D．正方形
3．如果一个四边形的面积正好等于它的两条对角线乘积的一半，那么这个四边形一定是（ ）．
A．菱形 B．矩形 C．正方形 D．对角线互相垂直的四边形
4．在下列图形中，沿着虚线将长方形剪成两部分，那么由这两部分既能拼成平行四边形，又能拼成三角形和梯形的是（ ）．
A B C D
5．梯形ABCD中，AB∥CD，若AD=m，CD=n，AB=m+n，则下列等式一定成立的是（ ）．
A．∠A=∠B B．∠D=2∠B C．BC=m-n D．BC=m+n
6．已知在正方形网格中如图1，每个小正方格都是边长为1的正方形，A、B两点在小正方格的顶点上，位置如图所示，点C也在小正方格的顶点上，且以A、B、C为顶点的三角形面积为1个平方单位，则点C的个数为（ ）．
A．3个 B．4个 C．5个 D．6个

二.填空题(每小题5分,共20分)
7.已知菱形的两条对角线长分别是6cm和8cm，则菱形的边长是
8.梯形ABCD中，AD∥BC，且AD：BC=3：5，梯形ABCD的面积是8cm2，点M、N分别是AD和BC上一点，E、F分别是BM、CM的中点，则四边形MENF的面积是_______cm2．

9．已知：右上图正方形ABCD的边长为8，M在DC上，且DM=2，N是AC上一动点，则DN+MN的最小值为_______．
10．以下图形：①矩形；②平行四边形；③正三角形；④等腰梯形；⑤菱形；⑥正方形．其中，既是中心对称图形，又是轴对称图形的有________．（填序号）
三.解答题(共56分,)
11.（10分） 如图，AD是△ABC的角平分线，DE∥AC交AB于E，DF∥AB交AC于F．
求证：AD⊥EF．
12．（10分）已知：正方形ABCD中，E为CD边上一点，F为BC延长线上一点，CE=CF，若∠BEC=60°，求∠EFD的度数．
13．（12分）如图，方格纸中的每个小方格都是边长为1个单位的正方形，Rt△ABC的顶点均在个点上，在建立平面直角坐标系后，点A的坐标为（－6，1），点B的坐标为（－3，1），点C的坐标为（－3，3）．
（1）将Rt△ABC沿x轴正方向平移5个单位得到Rt△A1B1C1，试在图上画出的图形Rt△A1B1C1，并写出点A1的坐标；
（2）将原来的Rt△ABC绕点B顺时针旋转90°得到Rt△A2B2C2，试在图上画出Rt△A2B2C2的图形．

14．（12分）已知：如图，在菱形ABCD中，E、F分别是BC、CD上的点，且CE=CF．过点C作CG∥EA交AF于H，交AD于G．若∠BAE=25°，∠BCD=130°，求∠AHC的度数．
15. （12分）如图，等腰梯形ＡＢＣＤ中，ＡＢ＝ＣＤ，ＡＤ∥ＢＣ，Ｅ是梯形外一点，
且ＥＡ＝ＥＤ，试说明ＥＢ＝ＥＣ
能力测试题
1．如图：在四边形ABCD中，E是AB上的一点，△ADE和△BCE都是等边三角形，点P、Q、M、N分别为AB、BC、CD、DA的中点，则四边形MNPQ是（ ）
A. 等腰梯形 B. 矩形 C. 菱形 D. 正方形
2．如下图，点P是边长为1的菱形ABCD对角线AC上一个动点，点M、N分别是AB、BC边上的中点，MP＋NP的最小值是( )
A．2 B．1 C． D．
3. 如图，正方形ABCD的边长为8，M在DC上，且DM=2，N是AC上一动点，则DN+MN的最小值为 .
4. 如图所示，在方格纸上建立的平面直角坐标系中，将△ABO绕点O按顺时针方向旋转90(，得△A(B(O ，则点A(的坐标为 .
5. 已知：如图在□ABCD中，AE是BC边上的高，将△ABE沿BC方向平移，使点E与点C重合，得△GFC.
⑴求证：BE(DG；
⑵若∠B(60(，当AB与BC满足什么数量关系时，四边形ABFG是菱形？证明你的结论.
6. 如图，P为Rt△ABC所在平面内任意一点(不在直线AC上)，
∠ACB = 90°，M为AB边中点．
操作：以PA、PC为邻边作平行四边形PADC，连结PM并延长到点E，使ME = PM，
连结DE．
（1）请你利用图14－2，选择Rt△ABC内的任意一点P按上述方法操作；
（2）经历（1）之后，观察两图形，猜想线段DE和线段BC之间有怎样的数量和位置关系？请选择其中的一个图形证明你的猜想；
（3）观察两图，你还可得出和DE 相关的什么结论？请直接写出．

特殊四边形（全章90分钟基础测试）
一.选择题(每小题3分,共36分)
1. 下列说法中，不正确的是（ ）．
（A）有三个角是直角的四边形是矩形;（B）对角线相等的四边形是矩形
（C）对角线互相垂直的矩形是正方形;（D）对角线互相垂直的平行四边形是菱形
2．已知一个四边形的对角线互相垂直，那么顺次连接这个四边形的四边中点所得的四边形是（ ）．
（A）矩形 （B）菱形 （C）等腰梯形 （D）正方形
3．如图2，矩形ABCD沿AE折叠，使点D落在BC边上的F点处，如果∠BAF=60°，那么∠DAE等于（ ）．
（A）15° （B）30° （C）45° （D）60°
3题 4题 5题
4．在菱形ABCD中，∠ADC=120°，则BD：AC等于（ ）．
（A）：2 （B）：3 （C）1：2 （D）：1
5．四边形ABCD是正方形，延长BC至点E，使CE=CA，连结AE交CD于点F，则∠AFC的度数是（ ）．
（A）150° （B）125° （C）135° （D）112．5°
6. 下列汽车标志中，是中心对称图形但不是轴对称图形的有（ ）个。
（A）2 （B）3 （C）4 （D）5
7、小明将下列 4张牌中的3张旋转180°后得到，

没有动的牌是（ ）。
（A）2 （B）4 （C）6 （D）8
8、四边形ABCD，仅从下列条件中任取两个加以组合，使得ABCD是平行四边形，一共有多少种不同的组合？（ ）
AB∥CD BC∥AD AB=CD BC=AD
（A）2组 （B）3组 （C）4组 （D）6组
9、下列说法错误的是（ ）
（A）一组对边平行且一组对角相等的四边形是平行四边形。
（B）每组邻边都相等的四边形是菱形。
（C）对角线互相垂直的平行四边形是正方形。
（D）四个角都相等的四边形是矩形。
10．小许拿了一张正方形的纸片如图甲，沿虚线对折一次得图乙．再对折一次得图丙．然后用剪刀沿图丙中的虚线（虚线与底边平行）剪去一个角．打开后的形状是（ ）．
11.矩形的边长为10cm和15cm，其中一个内角的角平分线分长边为两部份，这两部份的长为（）A.6cm和9cm B. 5cm和10cm C. 4cm和11cm D. 7cm和8cm12.如图，点E是正方形ABCD对角线AC上一点，AFBE于点F，交BD于点G，则下述结论中不成立的是（）A.AG=BE B.△ABG≌△BCE C.AE=DG D.∠AGD=∠DAG
二.填空题(每小题3分,共15分)
13. 要说明一个四边形是菱形,可以先说明这个四边形是 形,再说明 (只需填写一种方法)
14. 已知菱形的两条对角线长为12和6,那么这个菱形的面积为 .
15.既是轴对称图形，又是中心对称图形的四边形是_________．
16. 用一把刻度尺来判定一个零件是矩形的方法是 。
17.如图,是四边形ABCD的对称轴,如果AD∥BC,有下列结论: (1)AB∥CD;(2)AB=CD;(3)ABBC;(4)AO=OC.其中正确的结论是 .
(把你认为正确的结论的序号都填上)
三.解答题(共69分)
18．（8分）在一个平行四边形中若一个角的平分线把一条边分成长是2cm和3cm的两条线段，求该平行四边形的周长是多少？
19．（8分）如图，把一张长方形ABCD的纸片沿EF折叠后，ED与BC的交点为G，点D、C分别落在D′、C′的位置上，若∠EFG = 55?，求∠AEG和∠EGB的度数．
　　
　20．（9分）如图，一块正方形地板由全等的正方形瓷砖铺成，这地板的两条对角线上的瓷砖全是黑色，其余的瓷砖是白色的，如果有101块黑色瓷砖，那么瓷砖的总数是多少？
21. （12分）工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料(如图①),使AB=CD,EF=GH;
(2)摆放成如图②的四边形,则这时窗框的形状是 形,根据的数学道理是:
;
(3)将直角尺靠紧窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④),说明窗框合格,这时窗框是 形,根据的数学道理是:
.
(图①) (图②) (图③) (图④)
(第21题)
22．（10分）如图，△ABC中，点O是AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F．
　　(1)判断OE与OF的大小关系？并说明理由？
　　(2)当点O运动何处时，四边形AECF是矩形？并说出你的理由．
　　
　
　23．（10分）如图，若已知△ABC中，D、E分别为AB、AC的中点，则可得DE∥BC，且DE=BC．根据上面的结论：
　　(1)你能否说出顺次连结任意四边形各边中点，可得到一个什么特殊四边形？并说明理由．
　　(2)如果将(1)中的“任意四边形”改为条件是“平行四边形”或“菱形”或“矩形”或“等腰梯形”，那么它们的结论又分别怎样呢？请说明理由．
　　
24．（12分）如图，以△ABC的三边为边在BC的同侧分别作三个等边三角形，即△ABD、△BCE、△ACF，请回答下列问题，并说明理由．
　　(1)四边形ADEF是什么四边形？
　　(2)当△ABC满足什么条件时，四边形ADEF是矩形？
　　(3)当△ABC满足什么条件时，以A、D、E、F为顶点的四边形不存在．
　　
《1.1平行四边形及其性质(1)》课时训练参考答案
1.B 2.B 3.D 4．4cm(改为2cm)
5.
6. BC= 10cm CD=8cm CD=10cm
7. ∠A=40° ∠B=140° ∠C=40°∠D=140°
AB=CD=11 BC=AD=9
《1.1平行四边形及其性质（2）》课时训练参考答案
1.D 2.A 3.C 4. 8
5.答∵四边形ABCD是一个平行四边形，
∴△AOF≌△COE
∴OE=OF=1.1;AF=CE
∴四边形CDFE周长等于AB+BE+EF+AF=2.4+4+2.2=8.6
6.答：设一条对角线长为2a，则另一条对角线长为3a．
∵平行四边形周长等于68cm，∴相邻两边的长为 34cm，
∴34＋2a＋3a = 80，解得a = 9.2，
2a = 18.4，3a = 27.6．
即两条对角线的长度分别为18.4 cm 和3a = 27.6 cm．
《1.2平行四边形的判定》课时训练参考答案
1．c
2．B 点拨：熟练掌握平行四边形的判定定理是解答这类题目的关键．
3．B 点拨：可选择条件（1）（3）或（2）（4）或（1）（2）或（3）（4）．故有4种选法．
4．B 点拨：a2+b2+c2+d2=2ab+2cd即（a-b）2+（c-d）2=0，
即（a-b）2=0且（c-d）2=0．所以a=b，c=d，即两组对边分别相等，
所以四边形为平行四边形．
点拨：根据对角线互相平分的四边形为平行四边形来进行判别．
6.解：线段DE与BF的长度相等；连结BD交AC于O点，连结DF，BE，
如图所示．在ABCD中，DO=OB，AO=OC，又因为AF=EC，
所以AF-AO=CE-OC，即OF=OE，所以四边形DEBF是平行四边形，所以DE=BF．
点拨：本题若用三角形全等，也可以解答，但过程复杂，学了平行四边形性质后，要学会应用．
平行四边形的性质与判定(45分钟基础测试+能力测试题)参考答案
1．（C） 2．（C） 3．（C） 4.(D) 5.（C）6. (C) 7 . 3
8. 25°9. 18 ° 10. 25
11.因为BD=CD,所以又因为四边形ABCD是平行四边形,所以AD∥BC ,所以因为.
12.如图所示,连结对角线AC、BD,过A、B、C、D分别作BD、AC、BD、AC的平行线,且这些平行线两两相交于E、F、G、H,四边形EFGH即为符合条件的平行四边形.
13.（1）证明：当时，，
又，
四边形为平行四边形．
（2）证明：四边形为平行四边形，
．
．
14.证明：
猜想：，
证明：
证法一：如图19－1
四边形是平行四边形．

又

证法二：如图19－2连结，交于点，连结，．
四边形是平行四边形
，
又
四边形是平行四边形
15.（1）6，135°
（2） ∴
又 ∴四边形是平行四边形
（3）36
能力测试题答案
1．（C）答案：2.C 3.相等 点拨：利用“一组对边平行且相等的四边形是平行四边形”来确定．
4、证明：（1）在平行四边形中，∥，∴
又∵，∴，即
在与中，
， ∴．
（2）∵，∴，∴∥
5．解法一：是．理由：因为四边形ABCD是平行四边形，
所以AD=BC，AD∥BC，所以∠DAE=∠BCF．
在△ADE和△CBF中，因为
所以△ADE≌△CBF（S．A．S．）．所以DE=BF．
同理可证△ABE≌△CDF．所以BE=DF．
所以四边形DEBF是平行四边形（两组对边分别相等的四边形是平行四边形）．
解法二：是．理由：同解法一可证△ADE≌△CBF．所以DE=BF，∠AED=∠CFB．
所以180°-∠AED=180°-∠CFB．即∠DEF=∠BFE．所以DE∥BF．
所以四边形DEBF是平行四边形．（一组对边平行且相等的四边形是平行四边形）
解法三：是．理由：连结BD．如图，交AC于点O．
因为四边形ABCD是平行四边形，所以OA=OC，OB=OD．
又因为AE=CF，所以OA-AE=OC-CF，即OE=OF，
所以四边形DEBF是平行四边形（对角线互相平分的四边形是平行四边形）．
点拨：解法一利用了“两组对边分别相等的四边形是平行四边形”的判定方法；解法二利用了“一组对边平行且相等的四边形是平行四边形”的判定方法，解法三利用“对角线互相平分的四边形是平行四边形”的判别方法．
6.解：设第x秒时，四边形ABQP是平行四边形，即AP=BQ，
则AP=x，BQ=BC-CQ=6-2x，所以x=6-2x，解得x=2，
所以第2秒时，四边形ABQP是平行四边形．
《1.3特殊的平行四边形 矩形》课时训练参考答案
1.c 2.c3. 4. ABF≌△ADE，证明过程（略）
5．证四边形BDCE是平行四边形，得CE=BD=AC 。
6．∵四边形ABCD是矩形，∴∠C＝90°，AD∥BC ∵矩形纸片沿对角线BD折叠，使点C落在上的C’处，∴∠C’＝∠C＝90°，∠CBD＝∠EBD＝20°∵△CBD中，∠C’＝90°，∠EBD＝20°∴∠CDB＝70°又∵AD∥BC ∴∠EDB＝∠CBD＝20°∴∠C’DE＝50°
7．⑴相等且互相平分；⑵∵∠MAC＋∠NAC＝180°AB、AD分别平分∠MAC和∠NAC，∴∠BAC＋∠DAC＝90°，即∠BAD＝90°，同理，∠BCD＝90°∵MN∥PQ，∴∠MAC＋∠PCA＝180°（两直线平行，同旁内角互补）AB、CB分别平分∠MAC和∠PCA，∴∠BAC＋∠ACB＝90°，∴∠ABC＝90°∴四边形ABCD是矩形（有三个角是直角的四边形是矩形，∴AC、BD互相平分且相等（矩形的对角线相等且互相平分）。
《1.3特殊的平行四边形 菱形》课时训练参考答案
1.A 2. 32 3. 9.6 4. 24cm2
5.先证四边形ABEF是平行四边形，再由AE平分∠BAF，得∠FAE=∠BAE．又由∠FAE=∠AEB，得∠BAE=∠BEA，所以AB=BE，所以ABEF是菱形．
6.证明：(1) ∵四边形ABCD是菱形，∴AB=AD,,
∵BE=DF∴≌
∴AE=AF
(2) 连接AC∵AB=BC,
∴是等边三角形，E是BC的中点
∴AE⊥BC, ∴,同理
∵ ∴
又∵ AE=AF∴ 是等边三角形。
《1.3特殊的平行四边形 正方形》课时训练参考答案
1．D 2．D 3. 5㎝ 5√2 cm 25cm2 4. 8
5.
6.证明： ∵四边形ABCD是正方形
∴BC ＝ CD
﹙ 正方形的四条边都相等﹚
∵BE ＝ DF
∴EC ＝ FC
∵AC平分∠BCD
﹙ 正方形的每条对角线平分一组对角﹚
∴EF⊥ AC
∵AC ⊥BD
（正方形的对角线互相垂直）
∴ EF ∥ BD
《1.4特殊的平行四边形 图形的中心对称》课时训练参考答案
1. D 2. B 3. A 4.②④ 5.
6.说明：（1）C1(-1,-3) (2)C2(3,1) (3)A3(2,-2),B3(2,-1)
特殊四边形与图形的中心对称 (45分钟基础测试+能力测试题)参考答案
1．B 2．A 3．B 4.D 5．A 6．B 7．AC=BD；AB=BC 8．2；2 9．4cm2 10．5cm；24cm2
11．（1）BD=12cm，AC=12cm （2）S菱形ABCD=72cm2
12．略
13．图略
14．提示：只要证明△ABF≌△DAE
15．提示：（1）选用第一种铝板，最多能剪甲、乙两种零件各2个，共4个，
如图所示．S阴=300×500-2××200-2××150=10 000（mm）2
（2）剪切线如图所示:
《1.5特殊的平行四边形 梯形（1）》课时训练参考答案
1.C 2.B 3.A 4. 3 5. cm 6. 4
7. 解：∵在梯形ABCD中，DC＝AD＝BC，
∴∠DAB＝∠B，∠1＝∠3.又∵CD∥AB，
∴∠1＝∠2，∴∠2＝∠3，
∴∠B＝∠A＝2∠2
而AC⊥CB,∴∠ACB＝90°, ∴∠2＋∠B＝90°，即3∠2＝90°，∴∠2＝30°，
∴∠DAB＝∠B=2∠2＝60°，
∠D＝∠BCD＝120
《1.5特殊的平行四边形 梯形（2）》课时训练参考答案
1.B2.C3.C4. 7cm2
5.证明：依题意知DC∥BE，DC＝BE,
∴四边形BECD是平行四边形
∴∠E＝∠CDB,
又∵BA＝AB, ∠BAD＝∠ABC,AD＝BC
∴△BAD≌△ABC (SAS)
∴∠ABD＝∠BAC,而∠BCD＝∠ABD
∴∠E＝∠BAC ∴AC＝CE
6.解：四边形PQCD是平行四边形时，有PD＝QC，设s时为平行四边形，，，，，.
∴6s时它为平行四边形.
《1.6特殊的平行四边形中位线定理》课时训练参考答案
1.B 2. A 3. 7 4. 20m
5．由BO=DO和EA=EB得OE是中位线，所以OE∥BC
6．提示：证△AEM≌△FBM得ME=MB，
同理得NE=NC，于是MN是△EBC的中位线，即得结论
梯形与中位线定理(45分钟基础测试+能力测试题)参考答案
1.C 2.A 3.B 4．C 5．C 6．A
7. 2；8 8. 4 9. 2 10. 5
11.解：分别过A、D两点作AE⊥BC、DF⊥BC交BC于E、F两点，不难证明△ABE≌△DCF, ∴BE＝CF,而又可得EF＝AD＝3，∴BE＝CF＝2，在Rt△ABE中，
∴∠BAE＝30°，∴∠B=60°.
12.证明：依题意知DC∥BE，DC＝BE,
∴四边形BECD是平行四边形
∴∠E＝∠CDB,
又∵BA＝AB, ∠BAD＝∠ABC,AD＝BC
∴△BAD≌△ABC (SAS)
∴∠ABD＝∠BAC,而∠BCD＝∠ABD
∴∠E＝∠BAC ∴AC＝CE
13．提示：证明OE是△ABC的中位线
14、证明：（1）∵∥，，∴梯形为等腰梯形，∴．
又∵为中点，∴．
在与中，
， ∴
（2）∵∥，∴．
又∵平分，∴，
∴，∴．
又∵为中点，，
∴．
15.略
能力测试答案
1.B 2．C 3. 4 4. 2
5．提示：由EF为△AOD的中位线，得EF∥AD且EF=AD，
又因为AD∥BC且AD=BC，
所以EF∥BC且EF=BC，
故BECF为梯形．
又由△ABE≌△CDF（SAS）得EB=FC，
所以EBCF是等腰梯形
6.解：（1）第6步（2）证明AD∥BC
（3）不多余（4）一组对边平行且相等
（5）AD∥BC,AB＝DC且AB≠DC（6）不一定，也有可能是矩形.
特殊四边形（全章45分钟基础测试+能力测试题）答案
一、1．B 2．D 3．D 4．D 5．B 6．D
二7. 5cm 8．2．5  9．10 10．①⑤⑥
三11．证明略 提示：由DE∥AC且DF∥AB得AEDF为平行四边形；
由AD是△ABC的角平分线，得∠EAD=∠FAD，
又AE∥DF得∠EAD=∠ADF，
所以∠ADF=∠FAD，
从而AF=FD，
故平行四边形AEDF为菱形，
所以AD⊥EF
12．15° 13.略
14．100°
15证明：在等腰梯形ＡＢＣＤ中，
∵ＡＢ＝ＣＤ，ＡＤ∥ＢＣ
∴∠BAD＝∠ADC
∵EＡ＝EＤ
∴∠EAD＝∠EDA
∴∠BAE＝∠EDC
在△ABE和△CDB中
∵AB＝DC，∠BAE＝∠EDC，EA＝ED
∴△ABE≌△CDB
∴EB＝EC
能力测试题答案
1.C 2. 3. (1，3) 4. 10
5. 证明：⑴∵四边形ABCD是平行四边形，∴AB(CD.
∵AE是BC边上的高，且CG是由AE沿BC方向平移而成.
∴CG⊥AD.∴∠AEB(∠CGD(90(.
∵AE(CG，∴Rt△ABE≌Rt△CDG.
∴BE(DG.
⑵当BC(AB时，四边形ABFC是菱形.
∵AB∥GF，AG∥BF，∴四边形ABFG是平行四边形.
∵Rt△ABE中，∠B(60(，∴∠BAE(30(，∴BE(AB.
∵BE(CF，BC(AB，∴EF(AB.
∴AB(BF.∴四边形ABFG是菱形
6(1) 略 ; (2) DE∥BC，DE＝BC，; 证明5分 DB⊥AC.
证明方法:
特殊四边形（全章90分钟基础测试）答案
B 2．A 3．A 4．B 5．D 6.A 7.C 8.C 9.C 10．D 11.B 12.D
13.平行四边形;有一组邻边相等.
14. 36. 提示:菱形的面积等于菱形两条对角线乘积的一半.
15．答案不唯一
16.先测量两组对边是否相等，然后测量两条对角线是否相等。
17. (1)(2)(4). 提示:四边形ABCD是菱形.
18．14cm或16cm?
19．∠AEG = 70°，∠EGB = 110°
20．2601块?
21.(1)平行四边,两组对边分别相等的四边形是平行四边形;
(2)矩,有一个是直角的平行四边形是矩形.
22．提示：(1)相等；证OE=OC，OF=OC，推出OE=OF；
　　(2)当点O运动到AC的中点时，四边形AECF是矩形
23．(1)平行四边形；(2)平行四边形，矩形，菱形，正方形．
24．提示：(1)△DBE≌△ABC，得DB = AB = EF = AD，DE = AC = FC = FA，
　　即DE = FA，DA = FE得□ADEF；
　　(2)当∠BAC = 1500时是矩形，
　　(3)由△BDE≌△ABC知，∠BDE =∠BAC，∴∠BAC =∠BDE = 600+∠ADE，
　　当∠ADE = 00时，以A、D、E、F为顶点的四边形不存在，此时∠BAC = 600．