江西省铅山一中2020-2021学年高二下学期开学考试数学(文)试题 Word版含答案
文档属性
| 名称 | 江西省铅山一中2020-2021学年高二下学期开学考试数学(文)试题 Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-26 20:20:40 | ||
图片预览



文档简介
铅山一中开学考试数学(文科)
一、单选题
1.复数z满足(i为虚数单位),则( )
A.1 B.2 C. D.
2.命题“,”的否定是( )
A., B.,
C., D.,
3.某校有学生800人,其中女生有350人,为了解该校学生的体育锻炼情况,按男、女学生采用分层抽样法抽取容量为80的样本,则男生抽取的人数是( )
A.35 B.40 C.45 D.60
4.“一切金属都能导电,铁是金属,所以铁能导电”.此推理方法是( )
A.类比推理 B.演绎推理 C.归纳推理 D.以上都不对
5.某兴趣小组从包括甲、乙的小组成员中任选3人参加活动,若甲、乙至多有一人被选中的概率是,则甲、乙均被选中的概率是( )
A. B. C. D.
6.“椭圆的离心率为”是“”的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
7.某工厂从一批产品中抽取一个容量为的样本,根据样本数据分成,,,,四组,得到频率分布直方图如图所示.若样本数据落在内的个数是66,则( )
A.150 B.300 C.600 D.1200
8.若,满足约束条件,则的最大值为( )
A.30 B.14 C.25 D.36
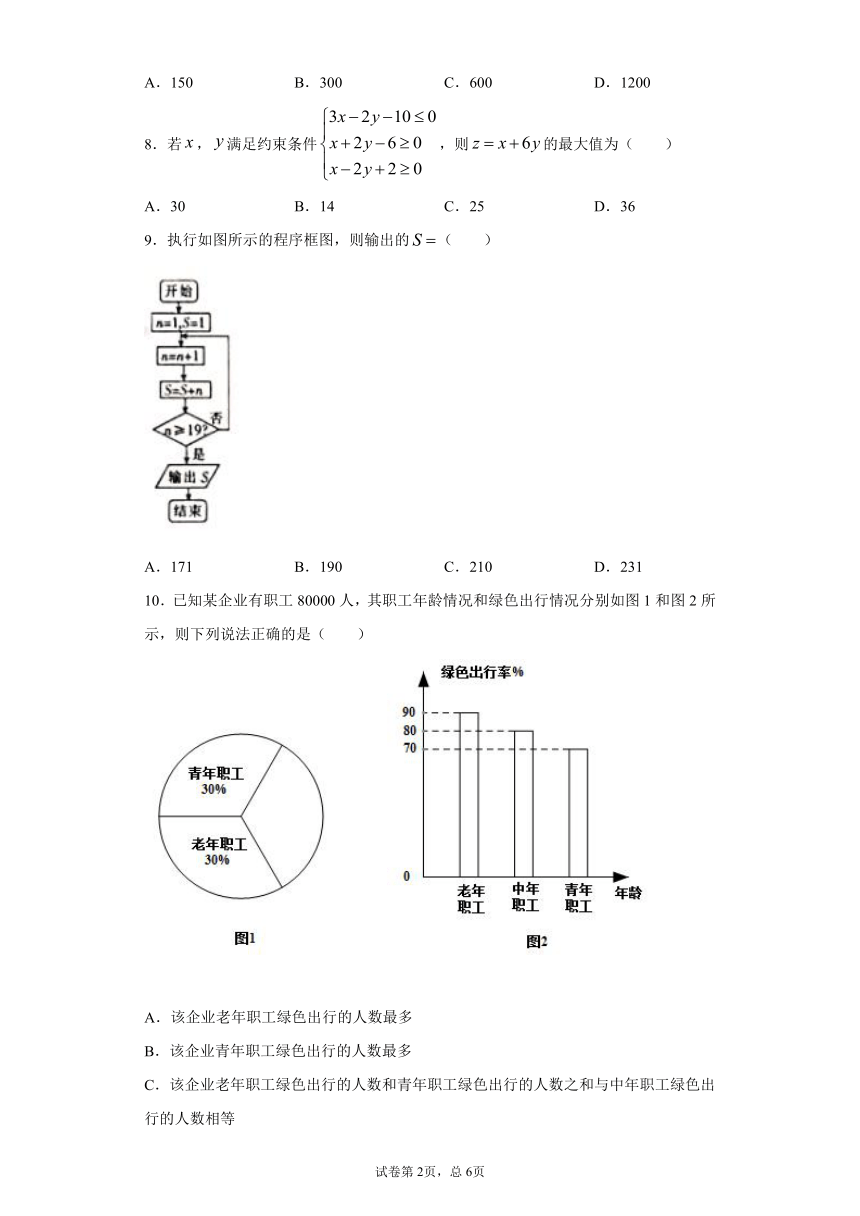
9.执行如图所示的程序框图,则输出的( )
A.171 B.190 C.210 D.231
10.已知某企业有职工80000人,其职工年龄情况和绿色出行情况分别如图1和图2所示,则下列说法正确的是( )
A.该企业老年职工绿色出行的人数最多
B.该企业青年职工绿色出行的人数最多
C.该企业老年职工绿色出行的人数和青年职工绿色出行的人数之和与中年职工绿色出行的人数相等
D.该企业绿色出行的人数占总人数的80%
11.已知椭圆:,过点的直线与椭圆交于,两点,若为线段的中点,则直线的斜率是( )
A. B. C. D.
12.在中,,,点,为所在平面内的一点,且满足,,若,则的最大值为( )
A. B. C. D.
二、填空题
13.某校歌手大奖赛比,选手的得分分别为9.4,9.5,9.0,8.7,9.8,则选手的平均分是______.
14.变量x,y满足约束条件,若的最大值为2,则实数_________.
15.已知为三角形内一点,且,现将一粒黄豆随机撒在三角形内,则黄豆落在三角形内的概率为______.
16.已知函数,,若,,使成立,则实数的取值范围是_________.
三、解答题
17.已知向量,.
(1)若,求;
(2)若,求向量在方向上的投影.
18.某校为了了解高三学生某次月考数学成绩的情况,抽取这次月考100名学生的数学成绩(分数都在内),按数学成绩分皮,,,,这5组,得到频率分布直方图如图所示.
(1)估计这次月考该校高三学生数学成绩的中位数(结果保留一位小数);
(2)若从数学成绩在内的学生中采用分层抽样的方法随机抽取5人,再从这5人中随机抽取2人,求至少有1人的数学成绩在内的概率.
19.已知命题:方程无实数根:命题:不等式在上恒成立.
(1)如果命题是假命题,请求出实数的取值范围;
(2)如果命题为真命题,且命题为假命题,请求出实数的取值范围.
20.某地区脐橙近几年的产量统计如下表:
年份 2015 2016 2017 2018 2019
年份代码 1 2 3 4 5
年产量(万吨) 7 7.1 7.2 7.4 7.8
(1)求年产量(万吨)关于年份代码的线性回归方程;
(2)根据(1)中所求的回归方程预测该地区2021年脐橙的年产量.
参考公式:,,,.
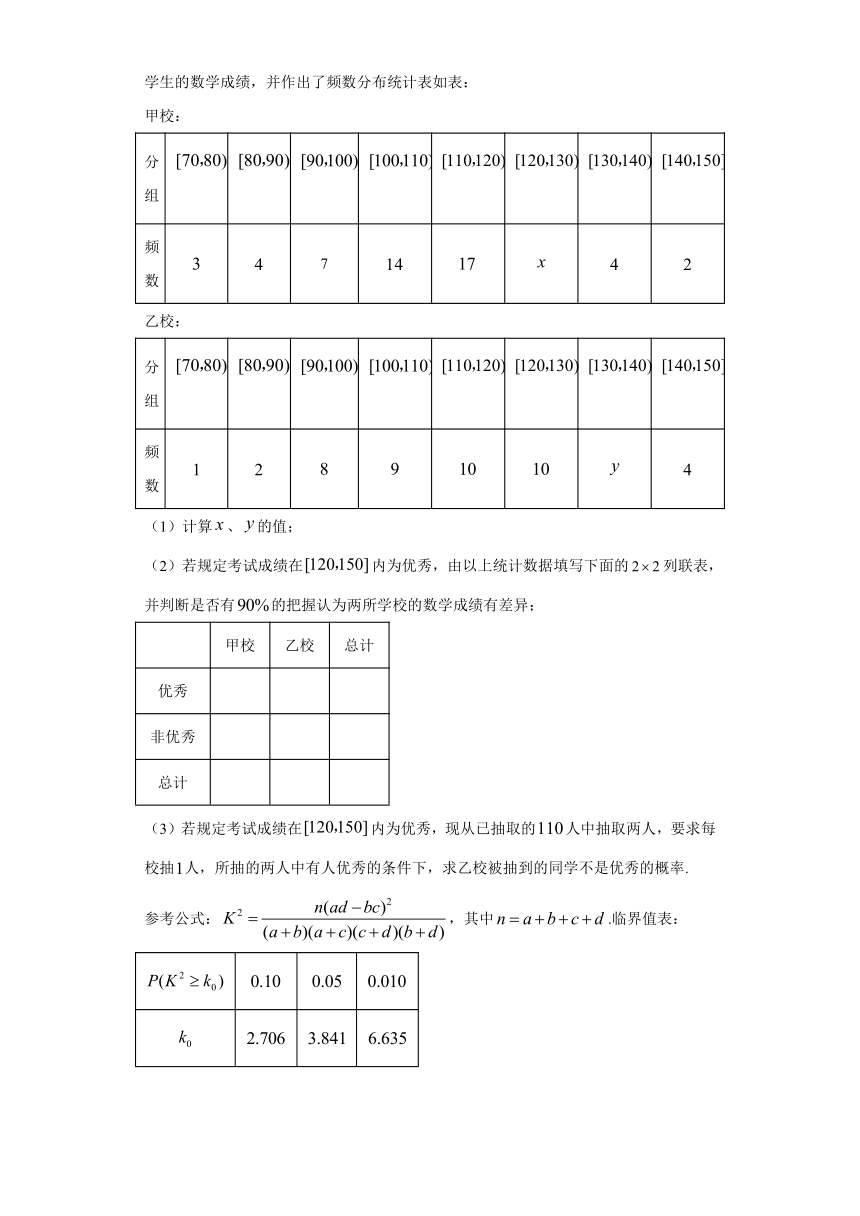
21.甲、乙两所学校高三年级分别有人,人,为了解两所学校全体高三年级学生在该地区五校联考的数学成绩情况,采用分层抽样方法从两所学校一共抽取了名学生的数学成绩,并作出了频数分布统计表如表:
甲校:
分组
频数
乙校:
分组
频数
(1)计算、的值;
(2)若规定考试成绩在内为优秀,由以上统计数据填写下面的列联表,并判断是否有的把握认为两所学校的数学成绩有差异;
甲校 乙校 总计
优秀
非优秀
总计
(3)若规定考试成绩在内为优秀,现从已抽取的人中抽取两人,要求每校抽人,所抽的两人中有人优秀的条件下,求乙校被抽到的同学不是优秀的概率.
参考公式:,其中.临界值表:
22.已知椭圆:()的离心率为,短轴长为2.
(1)求椭圆的标准方程;
(2)过点的直线与椭圆交于,两点若的面积为(为坐标原点),求直线的方程.
参考答案
1.C
【分析】
先将复数化成形式,再求模.
【详解】
由得,
∴,.
故选:C.
2.C
【分析】
根据全称命题“”的否定为特称命题“”即可得结果.
【详解】
因为全称命题的否定是特称命题,否定全称命题时,
一是要将全称量词改写为存在量词,二是否定结论,
所以,命题,的否定为,,
故选:C.
3.C
【分析】
利用分层抽样的定义直接求解即可
【详解】
由题意可得男生抽取的人数是.
故选:C
4.B
【分析】
符合三段论:大前提,小前提,结论,所以是演绎推理.
【详解】
在推理的过程中:一切金属都能导电,是大前提,
铁是金属,是小前提,
所以铁能导电,是结论,
故是演绎推理,
故选:B
5.B
【分析】
由事件“甲、乙至多有一人被选中”与事件“甲、乙均被选中”为对立事件,可求得答案
【详解】
由题意可知事件“甲、乙至多有一人被选中”与事件“甲、乙均被选中”为对立事件,则甲、乙均被选中的概率是.
故选:B
6.C
【分析】
由充分条件和必要条件的定义,结合椭圆的性质进行判断即可
【详解】
由椭圆的离心率为,得或;
由,得椭圆的离心率为.
故“椭圆的离心率为”是“”的必要不充分条件.
故选:C
7.A
【分析】
先由频率分布直方图求出数据落在内的频率,再由频率等于频数除以总数,可求得的值
【详解】
由图可知样本数据落在内的频率为,则.
故选:A
8.A
【分析】
画出约束条件所表示的平面区域,结合目标函数确定出最优解,代入即可求解.
【详解】
画出约束条件所标示平面区域,
把目标函数,化为直线,当直线平移到点A时,
此时直线在轴上的截距最大,目标函数取得最大值,
又由,解得,
所以目标函数的最大值为.
故选:A.
【点睛】
根据线性规划求解目标函数的最值问题的常见形式:
(1)截距型:形如 .求这类目标函数的最值常将函数 转化为直线的斜截式: ,通过求直线的截距的最值间接求出的最值;
(2)距离型:形如,转化为可行域内的点到定点的距离的平方,结合点到直线的距离公式求解;
(3)斜率型:形如,转化为可行域内点与定点的连线的斜率,结合直线的斜率公式,进行求解.
9.B
【分析】
根据所给数值,判断是否满足判断框中的条件,不满足继续循环,满足条件退出循环,得出结果.
【详解】
由题意可得.
;
;
;
;
;
,
则输出.
故选:B.
10.D
【分析】
由图先求出该企业老年职工绿色出行的人数、中年职工绿色出行的人数和青年职工绿色出行的人数,进而可得答案
【详解】
由图可知该企业老年职工绿色出行的人数是,中年职工绿色出行的人数是,青年职工绿色出行的人数是,则该企业职工绿色出行的人数占总人数的比例为,故A,B,C错误,D正确.
故选:D
11.C
【分析】
利用点差法,先得到,两式相减,利用中点坐标,求直线的斜率.
【详解】
设,,因为,在椭圆上,所以所以.因为为线段的中点,所以,,所以,则直线的斜率是.
故选:C
12.A
【分析】
根据题意,建立平面直角坐标系,由,根据向量坐标运算求出的坐标,设,由,得出点满足,根据圆的参数方程,可设点,根据,得出,最后利用化一公式和三角函数求最值,即可得出的最大值.
【详解】
解:由题意,以原点,,所直线为轴,轴建立直角坐标系,
则,,,
,,
设,因为,
所以点满足,
则可设点,
则由,得,
所以,
则的最大值为.
故选:A.
【点睛】
本题考查平面向量的坐标运算和模的求法,考查利用化一公式化简和三角函数求最值,还涉及圆的方程,考查转化思想和运算能力,属于中档题.
13.9.28
【分析】
直接用平均数的计算公式求平均数.
【详解】
由题意可得选手A的平均分是.
故答案为:9.28
14.3
【分析】
先画表示的区域,作出直线,向上平移直线时,增大,再作直线,根据的范围,确定可行域,观察能否取到最大值,然后由最大值为2可求得.
【详解】
先画表示的区域,作直线,直线中表示直线的纵截距,向上平移直线时,增大,作直线,分析可知,
当时,没有最大值2;
当时,目标函数对应的直线过直线和的交点时,取最大值,
代入,解得.
故答案为:3.
15.
【分析】
几何概型,只需要求三角形和的面积比即可得解.
【详解】
如图,延长交于点,
因为,所以为三角形的重心,则为的中点,.
设三角形的面积为,则三角形的面积为,故所求概率.
故答案为:
【点睛】
方法点睛:几何概型的基本类型:
(1)线段(弧长)比;
(2)面积比;
(3)体积比.
16.
【分析】
根据函数的单调性,分别求得函数和的值域构成的集合,结合题意,得到,列出不等式组,即可求解.
【详解】
由题意,函数在为单调递减函数,可得,
即函数的值域构成集合,
又由函数在区间上单调递增,可得,
即函数的值域构成集合,
又由,,使成立,即,
则满足,解得,
即实数的取值范围是.
故答案为:.
【点睛】
结论点睛:本题考查不等式的恒成立与有解问题,可按如下规则转化:
一般地,已知函数,
(1)若,,总有成立,故;
(2)若,,有成立,故;
(3)若,,有成立,故;
(4)若,,有,则的值域是值域的子集 .
17.(1);(2).
【分析】
(1)根据向量,,先求得的坐标,再根据,利用共线向量定理求解.
(2)由得到向量,再由向量在方向上的投影是求解.
【详解】
(1)因为向量,,
所以,
因为,
所以,
解得 ;
(2)当时,向量,,
所以向量在方向上的投影是 .
18.(1)100.5分;(2).
【分析】
(1)根据中位数左右两侧小矩形的面积之和都等于即可求解;
(2)先根据分层抽样计算数学成绩在和的人数,再利用古典概型概率公式计算即可求解.
【详解】
(1)因为,,
所以中位数在内.
设中位数为.则,
解得,即这次月考该校高三学生数学成绩的中位数约为100.5分.
(2)由题意可得这次月考数学成绩在的人数为,
这次月考数学成绩在的人数为,
则采用分层抽样的方法随机抽取的5人中,数学成绩在[110,130)的学生有3人,记为,,,数学成绩在的学生有2人,记为,.
从这5人中随机抽取人的情况有,,,,,,,,,,共10种,
其中符合条件的情况有,,,,,,,共7种,
故所求概率.
【点睛】
结论点睛:频率分布直方图的相关公式以及数字特征的计算,
①直方图中各个小长方形的面积之和为;
②直方图中每组样本的频数为频率乘以总数;
③最高的小矩形底边中点横坐标即是众数;
④中位数的左边和右边小长方形面积之和相等;
⑤平均数是频率分布直方图的重心,等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和.
19.(1)或;(2),或.
【分析】
(1)求出命题为真命题时m的取值范围,可得是假命题的取值范围;
(2)求出命题在上恒成立的取值范围,如果命题为真命题,且命题为假命题,则真假,或者假真,可求得答案.
【详解】
(1)命题:方程无实数根,则,得,
如果命题是假命题,则或.
(2)命题:不等式在上恒成立,
则,解得,
如果命题为真命题,且命题为假命题,则真假,或者假真,
当真假时,或,即,
当假真时,或,即,
综上所述,实数的取值范围为,或.
【点睛】
本题考查逻辑问题,涉及到的知识点有根据复合命题的真假判断求得参数的范围,利用补集的思想解决问题使其运算量减少,本题考查了一元二次不等式的解集与判别式的关系,考查了推理能力与计算能力.
20.(1);(2)8.06万吨.
【分析】
(1)由题意求和,再根据公式求和;(2)由题意可知,2021年对应的年份代码为7,即,代入回归直线方程,求的值.
【详解】
解:(1)由题意可得,,
,
,
,.
故年产量(万吨)关于年份代码的线性回归方程.
(2)由题意可知2021年对应的年份代码为7,即,
则(万吨),
即该地区2021年脐橙的年产量约为8.06万吨.
21.(1),;(2)分布列见解析,有;(3).
【分析】
(1)根据分层抽样比求出甲、乙抽取的人数,再根据表中数据即可求解.
(2)根据频数分布统计表可完善列联表,再计算观测值,对照表格即可判断.
(3)根据条件概率的计算公式即可求解.
【详解】
(1)从甲校抽(人),
从乙校抽(人),
根据表中数据可得,;
(2)表格填写如下,
甲校 乙校 总计
优秀
非优秀
总计
,
故有的把握认为两所学校的数学成绩有差异;
(3)设两校各取一人,有人优秀为事件,乙校学生不优秀为事件,
根据条件概率,则所求事件的概率.
22.(1);(2).
【分析】
(1)由椭圆的性质列方程可得,,即可得解;
(2)设直线的方程,联立方程组结合韦达定理可得,再由三角形面积即可解得,即可的解.
【详解】
(1)由题意可得,解得,,
故椭圆的标准方程为;
(2)由题意可知直线的斜率不为0,
则设直线的方程为,,.
联立,整理得,
,
则,,
故,
因为的面积为,所以,
设,则,整理得,解得,
所以,
故直线的方程为,即.
【点睛】
关键点点睛:解决本题的关键是将三角形面积转化为,结合韦达定理解方程即可得解.
试卷第6 66页,总6 66页
答案第14 1414页,总14 1414页
答案第13 1313页,总14 1414页
一、单选题
1.复数z满足(i为虚数单位),则( )
A.1 B.2 C. D.
2.命题“,”的否定是( )
A., B.,
C., D.,
3.某校有学生800人,其中女生有350人,为了解该校学生的体育锻炼情况,按男、女学生采用分层抽样法抽取容量为80的样本,则男生抽取的人数是( )
A.35 B.40 C.45 D.60
4.“一切金属都能导电,铁是金属,所以铁能导电”.此推理方法是( )
A.类比推理 B.演绎推理 C.归纳推理 D.以上都不对
5.某兴趣小组从包括甲、乙的小组成员中任选3人参加活动,若甲、乙至多有一人被选中的概率是,则甲、乙均被选中的概率是( )
A. B. C. D.
6.“椭圆的离心率为”是“”的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
7.某工厂从一批产品中抽取一个容量为的样本,根据样本数据分成,,,,四组,得到频率分布直方图如图所示.若样本数据落在内的个数是66,则( )
A.150 B.300 C.600 D.1200
8.若,满足约束条件,则的最大值为( )
A.30 B.14 C.25 D.36
9.执行如图所示的程序框图,则输出的( )
A.171 B.190 C.210 D.231
10.已知某企业有职工80000人,其职工年龄情况和绿色出行情况分别如图1和图2所示,则下列说法正确的是( )
A.该企业老年职工绿色出行的人数最多
B.该企业青年职工绿色出行的人数最多
C.该企业老年职工绿色出行的人数和青年职工绿色出行的人数之和与中年职工绿色出行的人数相等
D.该企业绿色出行的人数占总人数的80%
11.已知椭圆:,过点的直线与椭圆交于,两点,若为线段的中点,则直线的斜率是( )
A. B. C. D.
12.在中,,,点,为所在平面内的一点,且满足,,若,则的最大值为( )
A. B. C. D.
二、填空题
13.某校歌手大奖赛比,选手的得分分别为9.4,9.5,9.0,8.7,9.8,则选手的平均分是______.
14.变量x,y满足约束条件,若的最大值为2,则实数_________.
15.已知为三角形内一点,且,现将一粒黄豆随机撒在三角形内,则黄豆落在三角形内的概率为______.
16.已知函数,,若,,使成立,则实数的取值范围是_________.
三、解答题
17.已知向量,.
(1)若,求;
(2)若,求向量在方向上的投影.
18.某校为了了解高三学生某次月考数学成绩的情况,抽取这次月考100名学生的数学成绩(分数都在内),按数学成绩分皮,,,,这5组,得到频率分布直方图如图所示.
(1)估计这次月考该校高三学生数学成绩的中位数(结果保留一位小数);
(2)若从数学成绩在内的学生中采用分层抽样的方法随机抽取5人,再从这5人中随机抽取2人,求至少有1人的数学成绩在内的概率.
19.已知命题:方程无实数根:命题:不等式在上恒成立.
(1)如果命题是假命题,请求出实数的取值范围;
(2)如果命题为真命题,且命题为假命题,请求出实数的取值范围.
20.某地区脐橙近几年的产量统计如下表:
年份 2015 2016 2017 2018 2019
年份代码 1 2 3 4 5
年产量(万吨) 7 7.1 7.2 7.4 7.8
(1)求年产量(万吨)关于年份代码的线性回归方程;
(2)根据(1)中所求的回归方程预测该地区2021年脐橙的年产量.
参考公式:,,,.
21.甲、乙两所学校高三年级分别有人,人,为了解两所学校全体高三年级学生在该地区五校联考的数学成绩情况,采用分层抽样方法从两所学校一共抽取了名学生的数学成绩,并作出了频数分布统计表如表:
甲校:
分组
频数
乙校:
分组
频数
(1)计算、的值;
(2)若规定考试成绩在内为优秀,由以上统计数据填写下面的列联表,并判断是否有的把握认为两所学校的数学成绩有差异;
甲校 乙校 总计
优秀
非优秀
总计
(3)若规定考试成绩在内为优秀,现从已抽取的人中抽取两人,要求每校抽人,所抽的两人中有人优秀的条件下,求乙校被抽到的同学不是优秀的概率.
参考公式:,其中.临界值表:
22.已知椭圆:()的离心率为,短轴长为2.
(1)求椭圆的标准方程;
(2)过点的直线与椭圆交于,两点若的面积为(为坐标原点),求直线的方程.
参考答案
1.C
【分析】
先将复数化成形式,再求模.
【详解】
由得,
∴,.
故选:C.
2.C
【分析】
根据全称命题“”的否定为特称命题“”即可得结果.
【详解】
因为全称命题的否定是特称命题,否定全称命题时,
一是要将全称量词改写为存在量词,二是否定结论,
所以,命题,的否定为,,
故选:C.
3.C
【分析】
利用分层抽样的定义直接求解即可
【详解】
由题意可得男生抽取的人数是.
故选:C
4.B
【分析】
符合三段论:大前提,小前提,结论,所以是演绎推理.
【详解】
在推理的过程中:一切金属都能导电,是大前提,
铁是金属,是小前提,
所以铁能导电,是结论,
故是演绎推理,
故选:B
5.B
【分析】
由事件“甲、乙至多有一人被选中”与事件“甲、乙均被选中”为对立事件,可求得答案
【详解】
由题意可知事件“甲、乙至多有一人被选中”与事件“甲、乙均被选中”为对立事件,则甲、乙均被选中的概率是.
故选:B
6.C
【分析】
由充分条件和必要条件的定义,结合椭圆的性质进行判断即可
【详解】
由椭圆的离心率为,得或;
由,得椭圆的离心率为.
故“椭圆的离心率为”是“”的必要不充分条件.
故选:C
7.A
【分析】
先由频率分布直方图求出数据落在内的频率,再由频率等于频数除以总数,可求得的值
【详解】
由图可知样本数据落在内的频率为,则.
故选:A
8.A
【分析】
画出约束条件所表示的平面区域,结合目标函数确定出最优解,代入即可求解.
【详解】
画出约束条件所标示平面区域,
把目标函数,化为直线,当直线平移到点A时,
此时直线在轴上的截距最大,目标函数取得最大值,
又由,解得,
所以目标函数的最大值为.
故选:A.
【点睛】
根据线性规划求解目标函数的最值问题的常见形式:
(1)截距型:形如 .求这类目标函数的最值常将函数 转化为直线的斜截式: ,通过求直线的截距的最值间接求出的最值;
(2)距离型:形如,转化为可行域内的点到定点的距离的平方,结合点到直线的距离公式求解;
(3)斜率型:形如,转化为可行域内点与定点的连线的斜率,结合直线的斜率公式,进行求解.
9.B
【分析】
根据所给数值,判断是否满足判断框中的条件,不满足继续循环,满足条件退出循环,得出结果.
【详解】
由题意可得.
;
;
;
;
;
,
则输出.
故选:B.
10.D
【分析】
由图先求出该企业老年职工绿色出行的人数、中年职工绿色出行的人数和青年职工绿色出行的人数,进而可得答案
【详解】
由图可知该企业老年职工绿色出行的人数是,中年职工绿色出行的人数是,青年职工绿色出行的人数是,则该企业职工绿色出行的人数占总人数的比例为,故A,B,C错误,D正确.
故选:D
11.C
【分析】
利用点差法,先得到,两式相减,利用中点坐标,求直线的斜率.
【详解】
设,,因为,在椭圆上,所以所以.因为为线段的中点,所以,,所以,则直线的斜率是.
故选:C
12.A
【分析】
根据题意,建立平面直角坐标系,由,根据向量坐标运算求出的坐标,设,由,得出点满足,根据圆的参数方程,可设点,根据,得出,最后利用化一公式和三角函数求最值,即可得出的最大值.
【详解】
解:由题意,以原点,,所直线为轴,轴建立直角坐标系,
则,,,
,,
设,因为,
所以点满足,
则可设点,
则由,得,
所以,
则的最大值为.
故选:A.
【点睛】
本题考查平面向量的坐标运算和模的求法,考查利用化一公式化简和三角函数求最值,还涉及圆的方程,考查转化思想和运算能力,属于中档题.
13.9.28
【分析】
直接用平均数的计算公式求平均数.
【详解】
由题意可得选手A的平均分是.
故答案为:9.28
14.3
【分析】
先画表示的区域,作出直线,向上平移直线时,增大,再作直线,根据的范围,确定可行域,观察能否取到最大值,然后由最大值为2可求得.
【详解】
先画表示的区域,作直线,直线中表示直线的纵截距,向上平移直线时,增大,作直线,分析可知,
当时,没有最大值2;
当时,目标函数对应的直线过直线和的交点时,取最大值,
代入,解得.
故答案为:3.
15.
【分析】
几何概型,只需要求三角形和的面积比即可得解.
【详解】
如图,延长交于点,
因为,所以为三角形的重心,则为的中点,.
设三角形的面积为,则三角形的面积为,故所求概率.
故答案为:
【点睛】
方法点睛:几何概型的基本类型:
(1)线段(弧长)比;
(2)面积比;
(3)体积比.
16.
【分析】
根据函数的单调性,分别求得函数和的值域构成的集合,结合题意,得到,列出不等式组,即可求解.
【详解】
由题意,函数在为单调递减函数,可得,
即函数的值域构成集合,
又由函数在区间上单调递增,可得,
即函数的值域构成集合,
又由,,使成立,即,
则满足,解得,
即实数的取值范围是.
故答案为:.
【点睛】
结论点睛:本题考查不等式的恒成立与有解问题,可按如下规则转化:
一般地,已知函数,
(1)若,,总有成立,故;
(2)若,,有成立,故;
(3)若,,有成立,故;
(4)若,,有,则的值域是值域的子集 .
17.(1);(2).
【分析】
(1)根据向量,,先求得的坐标,再根据,利用共线向量定理求解.
(2)由得到向量,再由向量在方向上的投影是求解.
【详解】
(1)因为向量,,
所以,
因为,
所以,
解得 ;
(2)当时,向量,,
所以向量在方向上的投影是 .
18.(1)100.5分;(2).
【分析】
(1)根据中位数左右两侧小矩形的面积之和都等于即可求解;
(2)先根据分层抽样计算数学成绩在和的人数,再利用古典概型概率公式计算即可求解.
【详解】
(1)因为,,
所以中位数在内.
设中位数为.则,
解得,即这次月考该校高三学生数学成绩的中位数约为100.5分.
(2)由题意可得这次月考数学成绩在的人数为,
这次月考数学成绩在的人数为,
则采用分层抽样的方法随机抽取的5人中,数学成绩在[110,130)的学生有3人,记为,,,数学成绩在的学生有2人,记为,.
从这5人中随机抽取人的情况有,,,,,,,,,,共10种,
其中符合条件的情况有,,,,,,,共7种,
故所求概率.
【点睛】
结论点睛:频率分布直方图的相关公式以及数字特征的计算,
①直方图中各个小长方形的面积之和为;
②直方图中每组样本的频数为频率乘以总数;
③最高的小矩形底边中点横坐标即是众数;
④中位数的左边和右边小长方形面积之和相等;
⑤平均数是频率分布直方图的重心,等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和.
19.(1)或;(2),或.
【分析】
(1)求出命题为真命题时m的取值范围,可得是假命题的取值范围;
(2)求出命题在上恒成立的取值范围,如果命题为真命题,且命题为假命题,则真假,或者假真,可求得答案.
【详解】
(1)命题:方程无实数根,则,得,
如果命题是假命题,则或.
(2)命题:不等式在上恒成立,
则,解得,
如果命题为真命题,且命题为假命题,则真假,或者假真,
当真假时,或,即,
当假真时,或,即,
综上所述,实数的取值范围为,或.
【点睛】
本题考查逻辑问题,涉及到的知识点有根据复合命题的真假判断求得参数的范围,利用补集的思想解决问题使其运算量减少,本题考查了一元二次不等式的解集与判别式的关系,考查了推理能力与计算能力.
20.(1);(2)8.06万吨.
【分析】
(1)由题意求和,再根据公式求和;(2)由题意可知,2021年对应的年份代码为7,即,代入回归直线方程,求的值.
【详解】
解:(1)由题意可得,,
,
,
,.
故年产量(万吨)关于年份代码的线性回归方程.
(2)由题意可知2021年对应的年份代码为7,即,
则(万吨),
即该地区2021年脐橙的年产量约为8.06万吨.
21.(1),;(2)分布列见解析,有;(3).
【分析】
(1)根据分层抽样比求出甲、乙抽取的人数,再根据表中数据即可求解.
(2)根据频数分布统计表可完善列联表,再计算观测值,对照表格即可判断.
(3)根据条件概率的计算公式即可求解.
【详解】
(1)从甲校抽(人),
从乙校抽(人),
根据表中数据可得,;
(2)表格填写如下,
甲校 乙校 总计
优秀
非优秀
总计
,
故有的把握认为两所学校的数学成绩有差异;
(3)设两校各取一人,有人优秀为事件,乙校学生不优秀为事件,
根据条件概率,则所求事件的概率.
22.(1);(2).
【分析】
(1)由椭圆的性质列方程可得,,即可得解;
(2)设直线的方程,联立方程组结合韦达定理可得,再由三角形面积即可解得,即可的解.
【详解】
(1)由题意可得,解得,,
故椭圆的标准方程为;
(2)由题意可知直线的斜率不为0,
则设直线的方程为,,.
联立,整理得,
,
则,,
故,
因为的面积为,所以,
设,则,整理得,解得,
所以,
故直线的方程为,即.
【点睛】
关键点点睛:解决本题的关键是将三角形面积转化为,结合韦达定理解方程即可得解.
试卷第6 66页,总6 66页
答案第14 1414页,总14 1414页
答案第13 1313页,总14 1414页
同课章节目录
