1.5 一元一次不等式与一次函数

1.5 一元一次不等式与一次函数
第1题. 在一次函数中，为何值时，
（1）？ （2）？ （3）？
答案：解：（1）若，令，则．
即当时，一次函数中的值大于0．
（2）若，令，则．
即当时，一次函数中的值等于0．
（3）若，令，则．
即当时，一次函数中的值小于0．
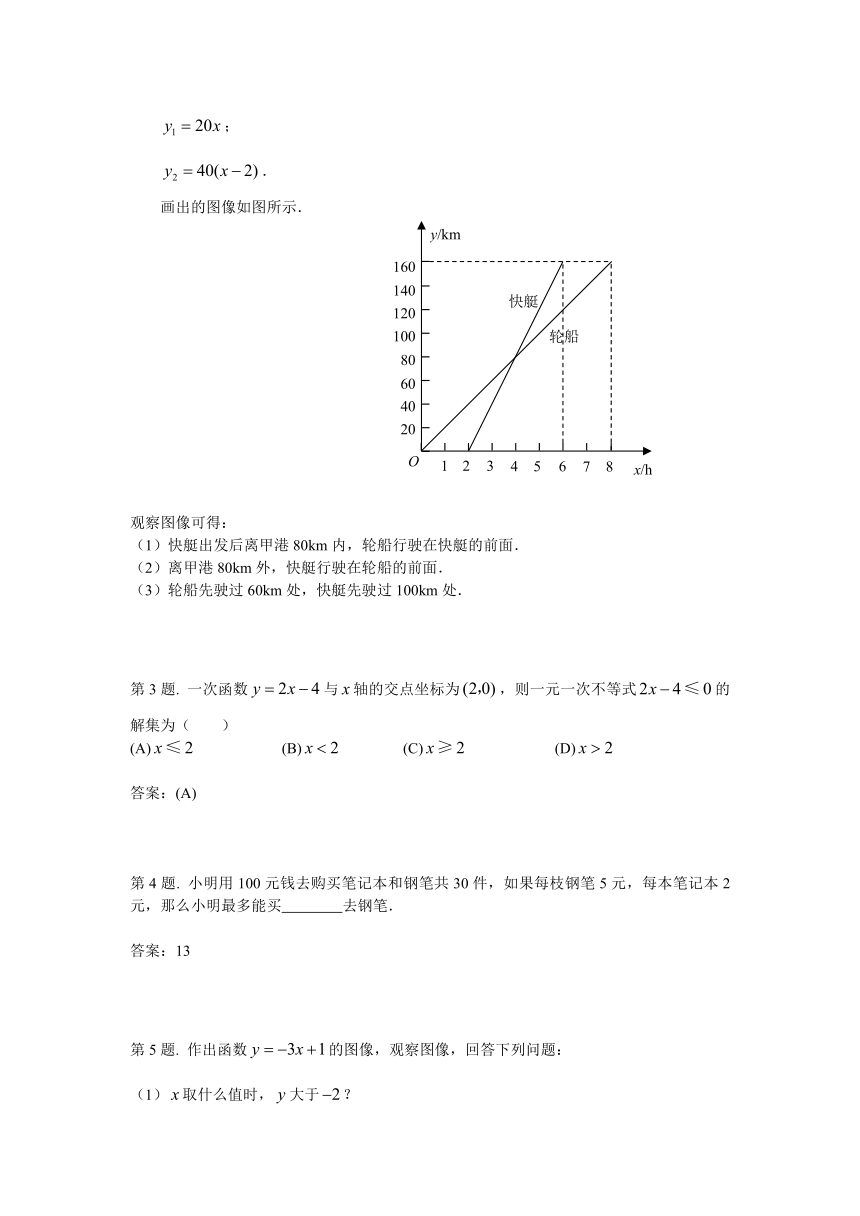
第2题. 一艘轮船以每小时20km的速度从甲港驶往160km远的乙港，2h后，一艘快艇以每小时40km的速度也从甲港驶往乙港．请你分别列出轮船和快艇行驶的路程(km)与时间(h)的函数关系式，在图中的直角坐标系中画出函数图像，并观察图像回答下列问题：
（1）何时轮船行驶在快艇的前面？
（2）何时快艇行驶在轮船的前面？
（3）哪一艘船先驶过60km？哪一艘船先驶过100km？
答案：解：轮船和快艇行驶的路程(km)与时间(h)的函数关系式分别为：
；
．
画出的图像如图所示．
观察图像可得：
（1）快艇出发后离甲港80km内，轮船行驶在快艇的前面．
（2）离甲港80km外，快艇行驶在轮船的前面．
（3）轮船先驶过60km处，快艇先驶过100km处．
第3题. 一次函数与轴的交点坐标为，则一元一次不等式的解集为（　　）
(A) (B) (C) (D)
答案：(A)
第4题. 小明用100元钱去购买笔记本和钢笔共30件，如果每枝钢笔5元，每本笔记本2元，那么小明最多能买　　　　去钢笔．
答案：13
第5题. 作出函数的图像，观察图像，回答下列问题：
（1）取什么值时，大于？
（2）取什么值时，小于？
（3）取什么值时，大于0．
答案：（1） （2） （3）
第6题. 已知，当取何值时，
答案：
第7题. 声音在空气中的传播速度(m/s)（简称音速）与气温(℃)满足关系式；
．
求音速超过349m/s时的气温．
答案：
第8题. 某单位急需用车，但又不准备买车，他们准备和一个个体车主或一国营出租车公司签定月租车合同．设汽车每月行驶，应付给个体车主的月费用为元，应付给汽车出租公司的月费用为元，分别与之间的函数关系图象（两条射线）如图所示，观察图象回答下列问题：
（1）每月行驶的路程在什么范围内，租国营公司的车合算？
（2）每月行驶的路程等于多少时，租两家车的费用相同？
（3）如果这个单位估计每月行驶的路程为2 300km，那么这个单位租哪家车合算？
答案：由图象可知：（1）每月行驶的路程小于1 500km时，租国营公司的汽车合算．
（2）每月行驶的路程为1 500km时，租两家车的费用相同．
（3）如果每月行驶的路程为2 300km，那么这个单位租个体车主的车合算．
第9题. 某移动通讯公司开设两种业务．“全球通”：先缴50元月租费，然后每通话1跳次，再付0.4元；“神州行”：不缴月租费，每通话1跳次，付话费0.6元（本题的通话均指市内通话）．若设一个月内通话跳次，两种方式的费用分别为元和元．
（跳次：1min为1跳次，不足1min按1跳次计算，如3.2min为4跳次．）
（1）写出与之间的函数关系式．
（2）一个月内通话多少跳次时，两种费用相同？一种费用大于另一种费用？
（3）某人估计一个月内通话300跳次，应选择哪一种合算？
答案：（1）．（为正整数）．
（2）当时，两种费用相同；当时，“全球通”的费用少于“神州行”的费用；当时，“全球通”的费用大于“神州行”的费用．
（3）应选择“全球通”合算．
1
2
3
4
5
6
7
8
20
40
60
80
100
120
140
160
y/km
x/h
O
1
2
3
4
5
6
7
8
20
40
60
80
100
120
140
160
y/km
x/h
O
轮船
快艇
0
500
1 500
2 500
1 000
2 000
3 000