第二十章 一次函数 单元测试卷 (含解析)
文档属性
| 名称 | 第二十章 一次函数 单元测试卷 (含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-27 07:10:13 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
一次函数
单元测试卷
一.选择题(共6小题)
1.下列函数中,一次函数是
A.
B.
C.
D.、是常数)
2.函数的图象不经过
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.下列各点,在一次函数的图象上的是
A.
B.
C.
D.
4.一次函数的图象经过
A.第一、二、三象限
B.第一、三、四象限
C.第一、二、四象限
D.第二、三、四象限
5.若一次函数的图象不经过第三象限,则、的取值范围是
A.,
B.,
C.,
D.,
6.在一次函数中,函数的值随的值增大而减小,那么常数的取值范围是
A.
B.
C.
D.
二.填空题(共12小题)
7.若是关于的一次函数,则
.
8.已知一次函数的图象经过点,则截距为
.
9.将直线向下平移2个单位,所得直线的表达式是
.
10.若直线平行直线,且过点,则
.
11.已知一次函数的图象与直线平行,那么
.
12.一次函数图象与坐标轴围成的三角形的面积是
.
13.如果把线沿轴向下平移1个单位,那么得到的直线的表达式为
.
14.把直线向左平移2个单位后,在轴上的截距为5,那么原来的直线解析式为
.
15.如果一次函数的图象经过点和,那么函数值随着自变量的增大而
.(填“增大”或“不变”或“减小”
16.如图.函数、为常数,的图象如图,则关于的不等式的解集为
.
17.某市出租车计费办法如图所示,如果小张在该市乘坐出租车行驶了10千米,那么小张需要支付的车费为
元.
18.我们知道:当时,不论取何实数,函数的值为3,所以直线一定经过定点;同样,直线一定经过的定点为
.
三.解答题(共7小题)
19.已知直线经过点和,求该直线的表达式.
20.已知一次函数的图象经过点,且平行于直线.
(1)求该一次函数的解析式;
(2)若点在该直线上,且在轴的下方,求的取值范围.
21.已知函数,
(1)若函数图象经过原点,求的值;
(2)若这个函数是一次函数,且随着的增大而减小,求的取值范围.
22.如图,过点的两条直线,分别交轴于点,,其中点在原点上方,点在原点下方,已知.
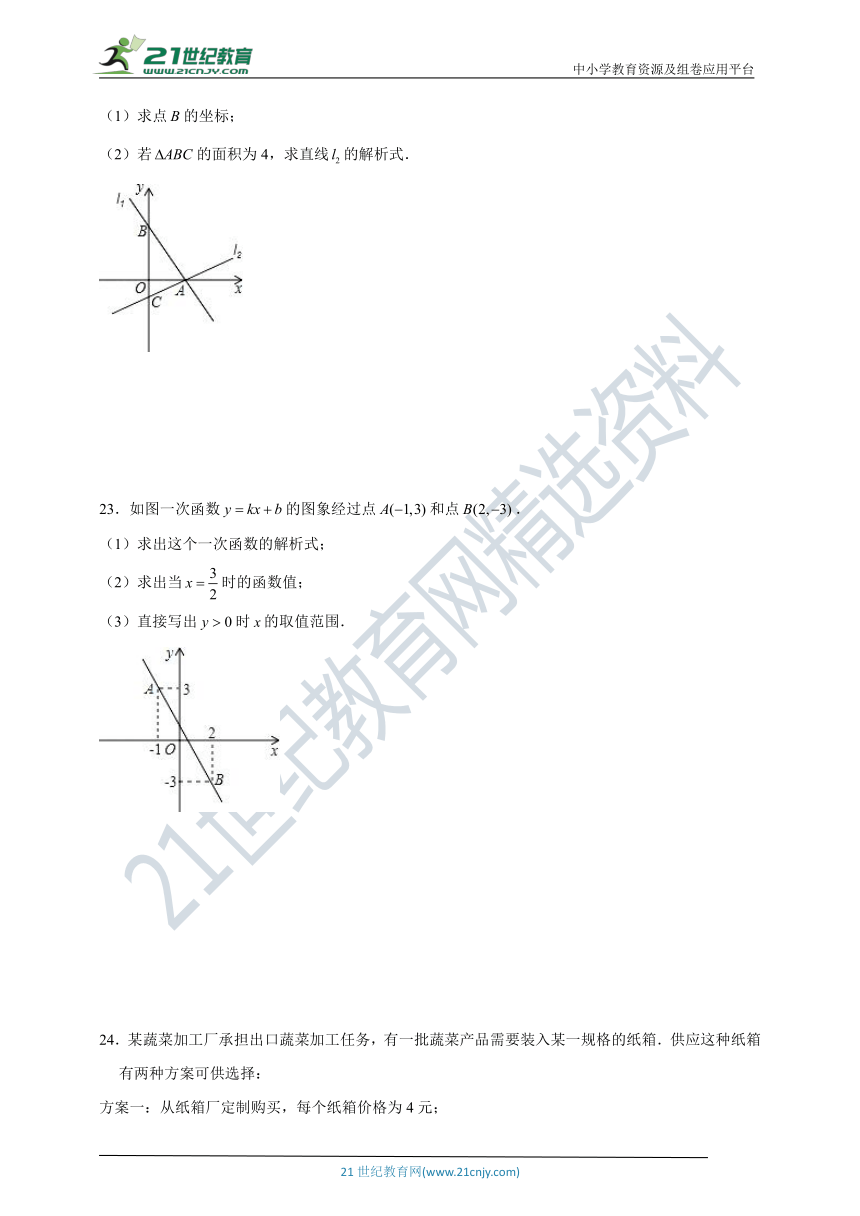
(1)求点的坐标;
(2)若的面积为4,求直线的解析式.
23.如图一次函数的图象经过点和点.
(1)求出这个一次函数的解析式;
(2)求出当时的函数值;
(3)直接写出时的取值范围.
24.某蔬菜加工厂承担出口蔬菜加工任务,有一批蔬菜产品需要装入某一规格的纸箱.供应这种纸箱有两种方案可供选择:
方案一:从纸箱厂定制购买,每个纸箱价格为4元;
方案二:由蔬菜加工厂租赁机器自己加工制作这种纸箱,机器租赁费按生产纸箱数收取.工厂需要一次性投入机器安装等费用16000元,每加工一个纸箱还需成本费2.4元.
(1)若需要这种规格的纸箱个,请分别写出从纸箱厂购买纸箱的费用(元和蔬菜加工厂自己加工制作纸箱的费用(元关于(个的函数关系式;
(2)假设你是决策者,你认为应该选择哪种方案?并说明理由.
25.周末,小明骑电动自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地.如图是他们离家的路程与小明离家时间的函数图象.已知妈妈驾车的速度是小明骑电动自行车速度的3倍.
(1)小明骑电动自行车的速度为
千米小时,在甲地游玩的时间为
小时;
(2)小明从家出发多少小时的时候被妈妈追上?此时离家多远?
参考答案
一.选择题(共6小题)
1.下列函数中,一次函数是
A.
B.
C.
D.、是常数)
解:、自变量在分母上,不符合一次函数定义;
、是二次函数,故选项错误;
、是正比例函数也是一次函数,故选项正确;
、少,不符合一次函数定义;
故选:.
2.函数的图象不经过
A.第一象限
B.第二象限
C.第三象限
D.第四象限
解:,,
函数的图象经过第一、三、四象限,
函数的图象不经过第二象限.
故选:.
3.下列各点,在一次函数的图象上的是
A.
B.
C.
D.
解:、当时,,
点在一次函数的图象上;
、当时,,
点不在一次函数的图象上;
、当时,,
点不在一次函数的图象上;
、当时,,
点不在一次函数的图象上.
故选:.
4.一次函数的图象经过
A.第一、二、三象限
B.第一、三、四象限
C.第一、二、四象限
D.第二、三、四象限
解:,
图象经过第一、三象限,
,
图象与轴的交点在轴上方,
一次函数的图象经过第一、二、三象限.
故选:.
5.若一次函数的图象不经过第三象限,则、的取值范围是
A.,
B.,
C.,
D.,
解:一次函数的图象不经过第三象限,
直线经过第一、二、四象限或第二、四象限,
,.
故选:.
6.在一次函数中,函数的值随的值增大而减小,那么常数的取值范围是
A.
B.
C.
D.
解:由题意得,
解得,
故选:.
二.填空题(共12小题)
7.若是关于的一次函数,则 1 .
解:由题意得:且,
解得:,
故答案为:1.
8.已知一次函数的图象经过点,则截距为 3 .
解:一次函数的图象经过点,
,
一次函数的截距为3.
故答案为:3.
9.将直线向下平移2个单位,所得直线的表达式是 .
解:由题意得:平移后的解析式为:,
即.所得直线的表达式是.
故答案为:.
10.若直线平行直线,且过点,则 .
解:若直线平行于直线,则,
且过点,当时,将其代入
解得:.
故答案为:.
11.已知一次函数的图象与直线平行,那么 4 .
解:一次函数的图象与直线平行,
,
,
故答案为:4.
12.一次函数图象与坐标轴围成的三角形的面积是 1 .
解:当时,,
一次函数的图象与轴交于点;
当时,,
解得:,
一次函数的图象与轴交于点.
一次函数的图象与坐标轴围成的三角形的面积.
故答案为:1.
13.如果把线沿轴向下平移1个单位,那么得到的直线的表达式为 .
解:把线沿轴向下平移1个单位,那么得到的直线的表达式为.
故答案为:.
14.把直线向左平移2个单位后,在轴上的截距为5,那么原来的直线解析式为 .
解:由“左加右减”的原则可知,若沿轴向左平移2个单位所得直线的解析式为,即,
在轴上的截距是5,
,
,
原来的直线解析式为:,
故答案为:.
15.如果一次函数的图象经过点和,那么函数值随着自变量的增大而 增大 .(填“增大”或“不变”或“减小”
解:时,;时,,
根据一次函数的单调性可得:函数值随着自变量的增大而增大.
故答案为:增大.
16.如图.函数、为常数,的图象如图,则关于的不等式的解集为 .
解:函数的图象经过点,并且函数值随的增大而减小,
所以当时,函数值大于0,即关于的不等式的解集是.
故答案为:.
17.某市出租车计费办法如图所示,如果小张在该市乘坐出租车行驶了10千米,那么小张需要支付的车费为 30.8 元.
解:由图象可知,出租车的起步价是14元,在3千米内只收起步价,
设超过3千米的函数解析式为,则,解得,
超过3千米时所需费用与之间的函数关系式是,
出租车行驶了10千米则(元,
故答案为30.8.
18.我们知道:当时,不论取何实数,函数的值为3,所以直线一定经过定点;同样,直线一定经过的定点为 .
解:根据题意,可化为:,
当时,不论取何实数,函数的值为6,
直线一定经过的定点为,
故答案为:.
三.解答题(共7小题)
19.已知直线经过点和,求该直线的表达式.
解:直线经过点和,
,
解得.
故该直线的解析式为.
20.已知一次函数的图象经过点,且平行于直线.
(1)求该一次函数的解析式;
(2)若点在该直线上,且在轴的下方,求的取值范围.
解:(1)一次函数的图象平行于直线,可设该一次函数解析式为,
将点代入得:,
解得:,
故一次函数解析式为:;
(2)点在轴下方,
,
解得:.
21.已知函数,
(1)若函数图象经过原点,求的值;
(2)若这个函数是一次函数,且随着的增大而减小,求的取值范围.
解:(1)把代入,得:,;
(2)根据随的增大而减小说明.即.
解得:.
22.如图,过点的两条直线,分别交轴于点,,其中点在原点上方,点在原点下方,已知.
(1)求点的坐标;
(2)若的面积为4,求直线的解析式.
解:(1)点,
点的坐标为;
(2)的面积为4
,即
设的解析式为,则
,解得
的解析式为
23.如图一次函数的图象经过点和点.
(1)求出这个一次函数的解析式;
(2)求出当时的函数值;
(3)直接写出时的取值范围.
解:(1)将与代入一次函数解析式得:,
解得:,
则一次函数解析式为:;
(2)将代入一次函数解析式得:;
(3)由题意得到,
解得:.
24.某蔬菜加工厂承担出口蔬菜加工任务,有一批蔬菜产品需要装入某一规格的纸箱.供应这种纸箱有两种方案可供选择:
方案一:从纸箱厂定制购买,每个纸箱价格为4元;
方案二:由蔬菜加工厂租赁机器自己加工制作这种纸箱,机器租赁费按生产纸箱数收取.工厂需要一次性投入机器安装等费用16000元,每加工一个纸箱还需成本费2.4元.
(1)若需要这种规格的纸箱个,请分别写出从纸箱厂购买纸箱的费用(元和蔬菜加工厂自己加工制作纸箱的费用(元关于(个的函数关系式;
(2)假设你是决策者,你认为应该选择哪种方案?并说明理由.
解:(1)从纸箱厂定制购买纸箱费用:,
蔬菜加工厂自己加工纸箱费用:.
(2),
由得,,
解得,
当时,,
选择方案一,从纸箱厂定制购买纸箱所需的费用低.
当时,,
选择方案二,加工厂自己加工制作纸箱所需的费用低.
当时,,
选择两个方案的费用相同.
25.周末,小明骑电动自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地.如图是他们离家的路程与小明离家时间的函数图象.已知妈妈驾车的速度是小明骑电动自行车速度的3倍.
(1)小明骑电动自行车的速度为 20 千米小时,在甲地游玩的时间为
小时;
(2)小明从家出发多少小时的时候被妈妈追上?此时离家多远?
解:(1)由图象得
在甲地游玩的时间是,
小明骑车速度:,
故答案为:20,0.5.
(2)如图,
妈妈驾车速度:
设直线的解析式为,
则,
解得:,
故直线的解析式为:.
小明走段与走段速度不变,
,
设直线解析式为,
把点代入得,
,
设直线解析式为,把点,
代入得:,
,
,
解得:,
.
答:小明出发1.75小时分钟)被妈妈追上,此时离家.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
一次函数
单元测试卷
一.选择题(共6小题)
1.下列函数中,一次函数是
A.
B.
C.
D.、是常数)
2.函数的图象不经过
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.下列各点,在一次函数的图象上的是
A.
B.
C.
D.
4.一次函数的图象经过
A.第一、二、三象限
B.第一、三、四象限
C.第一、二、四象限
D.第二、三、四象限
5.若一次函数的图象不经过第三象限,则、的取值范围是
A.,
B.,
C.,
D.,
6.在一次函数中,函数的值随的值增大而减小,那么常数的取值范围是
A.
B.
C.
D.
二.填空题(共12小题)
7.若是关于的一次函数,则
.
8.已知一次函数的图象经过点,则截距为
.
9.将直线向下平移2个单位,所得直线的表达式是
.
10.若直线平行直线,且过点,则
.
11.已知一次函数的图象与直线平行,那么
.
12.一次函数图象与坐标轴围成的三角形的面积是
.
13.如果把线沿轴向下平移1个单位,那么得到的直线的表达式为
.
14.把直线向左平移2个单位后,在轴上的截距为5,那么原来的直线解析式为
.
15.如果一次函数的图象经过点和,那么函数值随着自变量的增大而
.(填“增大”或“不变”或“减小”
16.如图.函数、为常数,的图象如图,则关于的不等式的解集为
.
17.某市出租车计费办法如图所示,如果小张在该市乘坐出租车行驶了10千米,那么小张需要支付的车费为
元.
18.我们知道:当时,不论取何实数,函数的值为3,所以直线一定经过定点;同样,直线一定经过的定点为
.
三.解答题(共7小题)
19.已知直线经过点和,求该直线的表达式.
20.已知一次函数的图象经过点,且平行于直线.
(1)求该一次函数的解析式;
(2)若点在该直线上,且在轴的下方,求的取值范围.
21.已知函数,
(1)若函数图象经过原点,求的值;
(2)若这个函数是一次函数,且随着的增大而减小,求的取值范围.
22.如图,过点的两条直线,分别交轴于点,,其中点在原点上方,点在原点下方,已知.
(1)求点的坐标;
(2)若的面积为4,求直线的解析式.
23.如图一次函数的图象经过点和点.
(1)求出这个一次函数的解析式;
(2)求出当时的函数值;
(3)直接写出时的取值范围.
24.某蔬菜加工厂承担出口蔬菜加工任务,有一批蔬菜产品需要装入某一规格的纸箱.供应这种纸箱有两种方案可供选择:
方案一:从纸箱厂定制购买,每个纸箱价格为4元;
方案二:由蔬菜加工厂租赁机器自己加工制作这种纸箱,机器租赁费按生产纸箱数收取.工厂需要一次性投入机器安装等费用16000元,每加工一个纸箱还需成本费2.4元.
(1)若需要这种规格的纸箱个,请分别写出从纸箱厂购买纸箱的费用(元和蔬菜加工厂自己加工制作纸箱的费用(元关于(个的函数关系式;
(2)假设你是决策者,你认为应该选择哪种方案?并说明理由.
25.周末,小明骑电动自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地.如图是他们离家的路程与小明离家时间的函数图象.已知妈妈驾车的速度是小明骑电动自行车速度的3倍.
(1)小明骑电动自行车的速度为
千米小时,在甲地游玩的时间为
小时;
(2)小明从家出发多少小时的时候被妈妈追上?此时离家多远?
参考答案
一.选择题(共6小题)
1.下列函数中,一次函数是
A.
B.
C.
D.、是常数)
解:、自变量在分母上,不符合一次函数定义;
、是二次函数,故选项错误;
、是正比例函数也是一次函数,故选项正确;
、少,不符合一次函数定义;
故选:.
2.函数的图象不经过
A.第一象限
B.第二象限
C.第三象限
D.第四象限
解:,,
函数的图象经过第一、三、四象限,
函数的图象不经过第二象限.
故选:.
3.下列各点,在一次函数的图象上的是
A.
B.
C.
D.
解:、当时,,
点在一次函数的图象上;
、当时,,
点不在一次函数的图象上;
、当时,,
点不在一次函数的图象上;
、当时,,
点不在一次函数的图象上.
故选:.
4.一次函数的图象经过
A.第一、二、三象限
B.第一、三、四象限
C.第一、二、四象限
D.第二、三、四象限
解:,
图象经过第一、三象限,
,
图象与轴的交点在轴上方,
一次函数的图象经过第一、二、三象限.
故选:.
5.若一次函数的图象不经过第三象限,则、的取值范围是
A.,
B.,
C.,
D.,
解:一次函数的图象不经过第三象限,
直线经过第一、二、四象限或第二、四象限,
,.
故选:.
6.在一次函数中,函数的值随的值增大而减小,那么常数的取值范围是
A.
B.
C.
D.
解:由题意得,
解得,
故选:.
二.填空题(共12小题)
7.若是关于的一次函数,则 1 .
解:由题意得:且,
解得:,
故答案为:1.
8.已知一次函数的图象经过点,则截距为 3 .
解:一次函数的图象经过点,
,
一次函数的截距为3.
故答案为:3.
9.将直线向下平移2个单位,所得直线的表达式是 .
解:由题意得:平移后的解析式为:,
即.所得直线的表达式是.
故答案为:.
10.若直线平行直线,且过点,则 .
解:若直线平行于直线,则,
且过点,当时,将其代入
解得:.
故答案为:.
11.已知一次函数的图象与直线平行,那么 4 .
解:一次函数的图象与直线平行,
,
,
故答案为:4.
12.一次函数图象与坐标轴围成的三角形的面积是 1 .
解:当时,,
一次函数的图象与轴交于点;
当时,,
解得:,
一次函数的图象与轴交于点.
一次函数的图象与坐标轴围成的三角形的面积.
故答案为:1.
13.如果把线沿轴向下平移1个单位,那么得到的直线的表达式为 .
解:把线沿轴向下平移1个单位,那么得到的直线的表达式为.
故答案为:.
14.把直线向左平移2个单位后,在轴上的截距为5,那么原来的直线解析式为 .
解:由“左加右减”的原则可知,若沿轴向左平移2个单位所得直线的解析式为,即,
在轴上的截距是5,
,
,
原来的直线解析式为:,
故答案为:.
15.如果一次函数的图象经过点和,那么函数值随着自变量的增大而 增大 .(填“增大”或“不变”或“减小”
解:时,;时,,
根据一次函数的单调性可得:函数值随着自变量的增大而增大.
故答案为:增大.
16.如图.函数、为常数,的图象如图,则关于的不等式的解集为 .
解:函数的图象经过点,并且函数值随的增大而减小,
所以当时,函数值大于0,即关于的不等式的解集是.
故答案为:.
17.某市出租车计费办法如图所示,如果小张在该市乘坐出租车行驶了10千米,那么小张需要支付的车费为 30.8 元.
解:由图象可知,出租车的起步价是14元,在3千米内只收起步价,
设超过3千米的函数解析式为,则,解得,
超过3千米时所需费用与之间的函数关系式是,
出租车行驶了10千米则(元,
故答案为30.8.
18.我们知道:当时,不论取何实数,函数的值为3,所以直线一定经过定点;同样,直线一定经过的定点为 .
解:根据题意,可化为:,
当时,不论取何实数,函数的值为6,
直线一定经过的定点为,
故答案为:.
三.解答题(共7小题)
19.已知直线经过点和,求该直线的表达式.
解:直线经过点和,
,
解得.
故该直线的解析式为.
20.已知一次函数的图象经过点,且平行于直线.
(1)求该一次函数的解析式;
(2)若点在该直线上,且在轴的下方,求的取值范围.
解:(1)一次函数的图象平行于直线,可设该一次函数解析式为,
将点代入得:,
解得:,
故一次函数解析式为:;
(2)点在轴下方,
,
解得:.
21.已知函数,
(1)若函数图象经过原点,求的值;
(2)若这个函数是一次函数,且随着的增大而减小,求的取值范围.
解:(1)把代入,得:,;
(2)根据随的增大而减小说明.即.
解得:.
22.如图,过点的两条直线,分别交轴于点,,其中点在原点上方,点在原点下方,已知.
(1)求点的坐标;
(2)若的面积为4,求直线的解析式.
解:(1)点,
点的坐标为;
(2)的面积为4
,即
设的解析式为,则
,解得
的解析式为
23.如图一次函数的图象经过点和点.
(1)求出这个一次函数的解析式;
(2)求出当时的函数值;
(3)直接写出时的取值范围.
解:(1)将与代入一次函数解析式得:,
解得:,
则一次函数解析式为:;
(2)将代入一次函数解析式得:;
(3)由题意得到,
解得:.
24.某蔬菜加工厂承担出口蔬菜加工任务,有一批蔬菜产品需要装入某一规格的纸箱.供应这种纸箱有两种方案可供选择:
方案一:从纸箱厂定制购买,每个纸箱价格为4元;
方案二:由蔬菜加工厂租赁机器自己加工制作这种纸箱,机器租赁费按生产纸箱数收取.工厂需要一次性投入机器安装等费用16000元,每加工一个纸箱还需成本费2.4元.
(1)若需要这种规格的纸箱个,请分别写出从纸箱厂购买纸箱的费用(元和蔬菜加工厂自己加工制作纸箱的费用(元关于(个的函数关系式;
(2)假设你是决策者,你认为应该选择哪种方案?并说明理由.
解:(1)从纸箱厂定制购买纸箱费用:,
蔬菜加工厂自己加工纸箱费用:.
(2),
由得,,
解得,
当时,,
选择方案一,从纸箱厂定制购买纸箱所需的费用低.
当时,,
选择方案二,加工厂自己加工制作纸箱所需的费用低.
当时,,
选择两个方案的费用相同.
25.周末,小明骑电动自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地.如图是他们离家的路程与小明离家时间的函数图象.已知妈妈驾车的速度是小明骑电动自行车速度的3倍.
(1)小明骑电动自行车的速度为 20 千米小时,在甲地游玩的时间为
小时;
(2)小明从家出发多少小时的时候被妈妈追上?此时离家多远?
解:(1)由图象得
在甲地游玩的时间是,
小明骑车速度:,
故答案为:20,0.5.
(2)如图,
妈妈驾车速度:
设直线的解析式为,
则,
解得:,
故直线的解析式为:.
小明走段与走段速度不变,
,
设直线解析式为,
把点代入得,
,
设直线解析式为,把点,
代入得:,
,
,
解得:,
.
答:小明出发1.75小时分钟)被妈妈追上,此时离家.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
