人教版九年级数学下册《第27章 相似数》单元测试题(Word版 有答案)
文档属性
| 名称 | 人教版九年级数学下册《第27章 相似数》单元测试题(Word版 有答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 404.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-26 00:00:00 | ||
图片预览

文档简介
人教版九年级数学下册《第27章
相似数》单元测试题
一.选择题(共10小题,每小题3分,满分30分)
1.已知,则的值为( )
A.2.5
B.
C.
D.
2.若,则的值为( )
A.
B.
C.
D.
3.如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC相似的是( )
A.
B.
C.
D.
4.如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,对于下列结论:①AC=FG;②四边形CBFG是矩形;③△ACD∽△FEQ.其中正确的是( )
A.①②③
B.①②
C.①③
D.②③
5.如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于( )
A.2
B.4
C.
D.
6.如图,在△ABC中,DE∥BC,AD=6,BD=3,AE=4,则AC的长为( )
A.9
B.7
C.6
D.5
7.如图所示,两个等边三角形,两个矩形,两个正方形,两个菱形各成一组,每组中的一个图形在另一个图形的内部,对应边平行,且对应边之间的距离都相等,那么两个图形不相似的一组是( )
A.
B.
C.
D.
8.如图,△ABC∽△ACD,相似比为2,则面积之比S△BDC:S△DAC为( )
A.4:1
B.3:1
C.2:1
D.1:1
9.如图,小明在打乒乓球时,为使球恰好能过网(设网高AB=15cm),且落在对方区域桌子底线C处,已知小明在自己桌子底线上方击球,则他击球点距离桌面的高度DE为( )
A.15cm
B.20cm
C.25cm
D.30cm
10.如图,已知∠ABC=90°,BD⊥AC于D,AB=4,AC=10,则AD=( )
A.
B.2
C.
D.1
二.填空题(共6小题,每小题3分,满分18分)
11.在直角△ABC中,AD是斜边BC上的高,BD=4,CD=9,则AD=
.
12.如图,AD是△ABC的中线,点E在AC延长线上,BE交AD的延长线于点F,若AC=2CE,则=
.
13.若△ABC∽△A′B′C′,∠A=50°,∠C=110°,则∠B′的度数为
.
14.如图,△DEF与△ABC位似,点O为位似中心,已知OF:OC=1:2,则△DEF与△ABC的周长之比是
.
15.《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD,从木杆的顶端D观察井水水岸C,视线DC与井口的直径AB交于点E,如果测得AB=1.6米,BD=1米,BE=0.2米,那么AC为
米.
16.已知△ABC,P是边AB上的一点,连接CP,请你添加一个条件,使△ACP∽△ABC,这个条件可以是
.(写出一个即可)
三.解答题(共8小题,满分62分)
17.(8分)如图,已知AD∥BE∥CF,如果AB=3,AC=7,EF=6.
(1)求DE的长.
(2)如果AC与DF相交于点O,OF=1,求.
18.(8分)已知:平行四边形ABCD,E是BA延长线上一点,CE与AD、BD交于G、F.
求证:CF2=GF?EF.
19.(8分)已知:如图,D是AC上一点,BE∥AC,BE=AD,AE分别交BD、BC于点F、G,且∠1=∠2.
(1)填空:图中与△BEF全等的三角形是
,与△BEF相似的三角形是
(不再添加任何辅助线);
(2)对(1)中的两个结论选择其中一个给予证明.
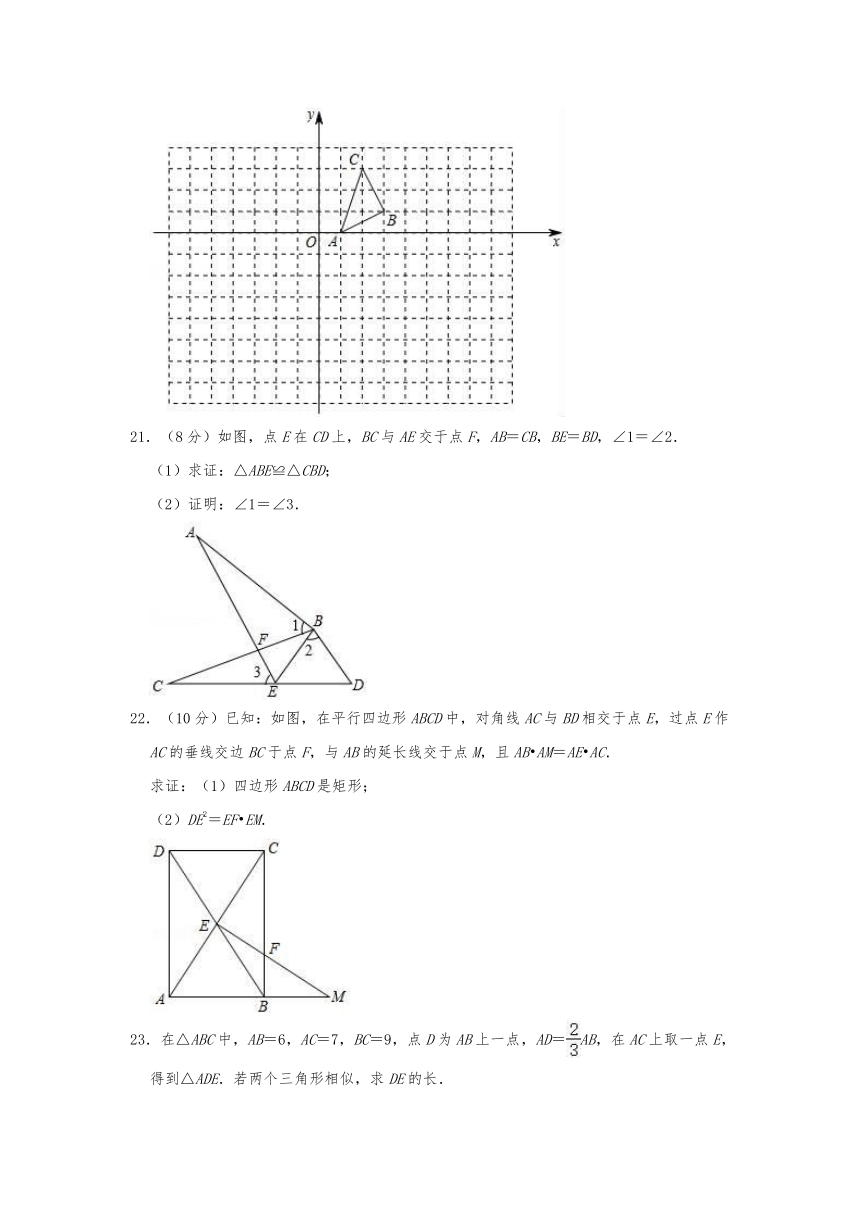
20.(8分)(1)作出将△ABC沿着x轴向左平移4个单位,再沿着y轴向上平移2个单位后的图形△A1B1C1,并写出点A1的坐标
;
(2)以原点O为位似中心,在原点的另一侧画出△A2B2C2,使.
21.(8分)如图,点E在CD上,BC与AE交于点F,AB=CB,BE=BD,∠1=∠2.
(1)求证:△ABE≌△CBD;
(2)证明:∠1=∠3.
22.(10分)已知:如图,在平行四边形ABCD中,对角线AC与BD相交于点E,过点E作AC的垂线交边BC于点F,与AB的延长线交于点M,且AB?AM=AE?AC.
求证:(1)四边形ABCD是矩形;
(2)DE2=EF?EM.
23.在△ABC中,AB=6,AC=7,BC=9,点D为AB上一点,AD=AB,在AC上取一点E,得到△ADE.若两个三角形相似,求DE的长.
24.(12分)在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm,现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动,如果点P的速度是4cm/s,点Q的速度是2cm/s,它们同时出发,当有一点到达所在线段的端点时,就停止运动.设运动时间为t秒.求:
(1)当t=3时,这时,P,Q两点之间的距离是多少?
(2)若△CPQ的面积为S,求S关于t的函数关系式.
(3)当t为多少时,以点C,P,Q为顶点的三角形与△ABC相似?
参考答案
一.选择题
1.解:∵,
∴b=a,
∴==.
故选:B.
2.解:∵,
∴y=x,
∴==.
故选:C.
3.解:∵小正方形的边长均为1
∴△ABC三边分别为2,,
同理:A中各边的长分别为:,3,;
B中各边长分别为:,1,;
C中各边长分别为:1、2,;
D中各边长分别为:2,,;
∵只有B项中的三边与已知三角形的三边对应成比例,且相似比为
故选:B.
4.解:①∵四边形ADEF为正方形,
∴∠FAD=90°,AD=AF=EF,
∴∠CAD+∠FAG=90°,
∵FG⊥CA,
∴∠GAF+∠AFG=90°,
∴∠CAD=∠AFG,
在△FGA和△ACD中,,
∴△FGA≌△ACD(AAS),
∴AC=FG.
故正确;
②∵BC=AC,
∴FG=BC,
∵∠ACB=90°,FG⊥CA,
∴FG∥BC,
∴四边形CBFG是矩形.
故正确;
③∵∠FQE=∠DQB=∠ADC,∠E=∠C=90°,
∴△ACD∽△FEQ.
故正确.
综上所述,正确的结论是①②③.
故选:A.
5.解:∵AB∥CD∥EF,
∴=,即=,
∴BC=,
∴CE=BE﹣BC=12﹣=.
故选:C.
6.解:∵DE∥BC,AD=6,BD=3,AE=4,
∴,
∴EC=2,
∴AC=2+4=6.
故选:C.
7.解:由题意得,A中三角形对应角相等,对应边成比例,两三角形相似;
C,D中正方形,菱形四条边均相等,所以对应边成比例,又角也相等,所以正方形,菱形相似;
而B中矩形四个角相等,但对应边不一定成比例,所以B中矩形不是相似多边形.
故选:B.
8.解:∵△ABC∽△ACD,相似比为2,
∴S△ABC:S△ACD=4,
∴S△BDC:S△ACD=3:1.
故选:B.
9.解:∵AB∥DE,
∴△CAB∽△CDE,
∴=,
而BC=BE,
∴DE=2AB=2×15=30(cm).
故选:D.
10.解:根据射影定理得:AB2=AD?AC,
∴AD==.
故选:A.
二.填空题
11.解:
∵△ABC是直角三角形,AD是斜边BC上的高,
∴AD2=BD?CD(射影定理),
∵BD=4,CD=9,
∴AD=6.
12.解:如图,过点DG作DG∥AE,交BE于点G;
∵AD是△ABC的中线,
∴DG=,
∵AC=2CE,
∴DG=AC,
∴=,
=,
即=5,
故答案为5.
13.解:∵∠A=50°,∠C=110°,
∴∠B=180°﹣50°﹣110°=20°,
∵△ABC∽△A′B′C′,
∴∠B′=∠B=20°.
故答案为20°.
14.解:∵△DEF与△ABC位似,点O为位似中心,
∴△DEF与△ABC的周长之比是:1:2.
故答案为:1:2.
15.解:∵BD⊥AB,AC⊥AB,
∴BD∥AC,
∴△ACE∽△BDE,
∴,
∴=,
∴AC=7(米),
故答案为:7.
16.解:∵∠A=∠A,
∴当∠ACP=∠B,或∠APC=∠ACB或=时,△ACP∽△ABC,
故答案为:∠ACP=∠B,或∠APC=∠ACB或=.
三.解答题
17.解:(1)∵AD∥BE∥CF,
∴=,即=,
∴DE=;
(2)∵OF=1,
∴OE=6﹣1=5,
∴OD=5+=,
∵AD∥CF,
∴===.
18.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴=,=,
∴=,
即CF2=GF?EF.
19.(1)解:△BEF≌△DAF,△BEF∽△GBF;
(2)证明:∵BE∥AC,
∴∠1=∠E,
在△BEF和△DAF中,
∵,
∴△BEF≌△DAF(AAS);
∵BE∥AC,
∴∠1=∠E,
∵∠1=∠2,
∴∠2=∠E,
又∵∠F为公共角,
∴△BEF∽△GBF.
20.解:(1)如图所示:△A1B1C1,即为所求,点A1的坐标为:(﹣3,2);
故答案为:(﹣3,2);
(2)如图所示:△A2B2C2,即为所求.
21.证明:(1)∵∠1=∠2,
∴∠1+∠CBE=∠2+∠CBE,即∠ABE=∠CBD,
在△ABE和△CBD中,
,
∴△ABE≌△CBD(SAS);
(2)∵△ABE≌△CBD,
∴∠A=∠C,
∵∠AFB=∠CFE,
∴∠1=∠3.
22.解:(1)∵AB?AM=AE?AC,
∴=,
∵∠CAB=∠CAB,
∴△ACB∽△AME,
∴∠AME=∠ACB,
由于∠AME+∠BAC=90°,
则∠ACB+∠BAC=90°,
∴?ABCD是矩形.
(2)由(1)可知:DE=EC,AE=EC,
∵ME⊥AC,
∴ME平分∠AMC,
∴∠CME=∠AME=∠ECB,
∵∠MEC=∠FEC=90°,
∴△CEF∽△MEC,
∴,
∴EC2=EF?EM,
即DE2=EF?EM
23.解:∵∠A是公共角,
∴当=,即=时,△ADE∽△ABC,
解得:DE=6;
当=,即=时,△ADE∽△ACB,
解得:DE=,
综上可得:当DE=6或时,△ADE与原三角形相似.
24.解:由题意得AP=4t,CQ=2t,则CP=20﹣4t,
(1)当t=3时,CP=20﹣4t=8cm,CQ=2t=6cm,
由勾股定理得PQ=;
(2)由题意得AP=4t,CQ=2t,则CP=20﹣4t,
因此Rt△CPQ的面积为S=cm2;
(3)分两种情况:
①当Rt△CPQ∽Rt△CAB时,,即,解得t=3;
②当Rt△CPQ∽Rt△CBA时,,即,解得t=.
因此t=3或t=时,以点C、P、Q为顶点的三角形与△ABC相似.
相似数》单元测试题
一.选择题(共10小题,每小题3分,满分30分)
1.已知,则的值为( )
A.2.5
B.
C.
D.
2.若,则的值为( )
A.
B.
C.
D.
3.如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC相似的是( )
A.
B.
C.
D.
4.如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,对于下列结论:①AC=FG;②四边形CBFG是矩形;③△ACD∽△FEQ.其中正确的是( )
A.①②③
B.①②
C.①③
D.②③
5.如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于( )
A.2
B.4
C.
D.
6.如图,在△ABC中,DE∥BC,AD=6,BD=3,AE=4,则AC的长为( )
A.9
B.7
C.6
D.5
7.如图所示,两个等边三角形,两个矩形,两个正方形,两个菱形各成一组,每组中的一个图形在另一个图形的内部,对应边平行,且对应边之间的距离都相等,那么两个图形不相似的一组是( )
A.
B.
C.
D.
8.如图,△ABC∽△ACD,相似比为2,则面积之比S△BDC:S△DAC为( )
A.4:1
B.3:1
C.2:1
D.1:1
9.如图,小明在打乒乓球时,为使球恰好能过网(设网高AB=15cm),且落在对方区域桌子底线C处,已知小明在自己桌子底线上方击球,则他击球点距离桌面的高度DE为( )
A.15cm
B.20cm
C.25cm
D.30cm
10.如图,已知∠ABC=90°,BD⊥AC于D,AB=4,AC=10,则AD=( )
A.
B.2
C.
D.1
二.填空题(共6小题,每小题3分,满分18分)
11.在直角△ABC中,AD是斜边BC上的高,BD=4,CD=9,则AD=
.
12.如图,AD是△ABC的中线,点E在AC延长线上,BE交AD的延长线于点F,若AC=2CE,则=
.
13.若△ABC∽△A′B′C′,∠A=50°,∠C=110°,则∠B′的度数为
.
14.如图,△DEF与△ABC位似,点O为位似中心,已知OF:OC=1:2,则△DEF与△ABC的周长之比是
.
15.《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD,从木杆的顶端D观察井水水岸C,视线DC与井口的直径AB交于点E,如果测得AB=1.6米,BD=1米,BE=0.2米,那么AC为
米.
16.已知△ABC,P是边AB上的一点,连接CP,请你添加一个条件,使△ACP∽△ABC,这个条件可以是
.(写出一个即可)
三.解答题(共8小题,满分62分)
17.(8分)如图,已知AD∥BE∥CF,如果AB=3,AC=7,EF=6.
(1)求DE的长.
(2)如果AC与DF相交于点O,OF=1,求.
18.(8分)已知:平行四边形ABCD,E是BA延长线上一点,CE与AD、BD交于G、F.
求证:CF2=GF?EF.
19.(8分)已知:如图,D是AC上一点,BE∥AC,BE=AD,AE分别交BD、BC于点F、G,且∠1=∠2.
(1)填空:图中与△BEF全等的三角形是
,与△BEF相似的三角形是
(不再添加任何辅助线);
(2)对(1)中的两个结论选择其中一个给予证明.
20.(8分)(1)作出将△ABC沿着x轴向左平移4个单位,再沿着y轴向上平移2个单位后的图形△A1B1C1,并写出点A1的坐标
;
(2)以原点O为位似中心,在原点的另一侧画出△A2B2C2,使.
21.(8分)如图,点E在CD上,BC与AE交于点F,AB=CB,BE=BD,∠1=∠2.
(1)求证:△ABE≌△CBD;
(2)证明:∠1=∠3.
22.(10分)已知:如图,在平行四边形ABCD中,对角线AC与BD相交于点E,过点E作AC的垂线交边BC于点F,与AB的延长线交于点M,且AB?AM=AE?AC.
求证:(1)四边形ABCD是矩形;
(2)DE2=EF?EM.
23.在△ABC中,AB=6,AC=7,BC=9,点D为AB上一点,AD=AB,在AC上取一点E,得到△ADE.若两个三角形相似,求DE的长.
24.(12分)在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm,现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动,如果点P的速度是4cm/s,点Q的速度是2cm/s,它们同时出发,当有一点到达所在线段的端点时,就停止运动.设运动时间为t秒.求:
(1)当t=3时,这时,P,Q两点之间的距离是多少?
(2)若△CPQ的面积为S,求S关于t的函数关系式.
(3)当t为多少时,以点C,P,Q为顶点的三角形与△ABC相似?
参考答案
一.选择题
1.解:∵,
∴b=a,
∴==.
故选:B.
2.解:∵,
∴y=x,
∴==.
故选:C.
3.解:∵小正方形的边长均为1
∴△ABC三边分别为2,,
同理:A中各边的长分别为:,3,;
B中各边长分别为:,1,;
C中各边长分别为:1、2,;
D中各边长分别为:2,,;
∵只有B项中的三边与已知三角形的三边对应成比例,且相似比为
故选:B.
4.解:①∵四边形ADEF为正方形,
∴∠FAD=90°,AD=AF=EF,
∴∠CAD+∠FAG=90°,
∵FG⊥CA,
∴∠GAF+∠AFG=90°,
∴∠CAD=∠AFG,
在△FGA和△ACD中,,
∴△FGA≌△ACD(AAS),
∴AC=FG.
故正确;
②∵BC=AC,
∴FG=BC,
∵∠ACB=90°,FG⊥CA,
∴FG∥BC,
∴四边形CBFG是矩形.
故正确;
③∵∠FQE=∠DQB=∠ADC,∠E=∠C=90°,
∴△ACD∽△FEQ.
故正确.
综上所述,正确的结论是①②③.
故选:A.
5.解:∵AB∥CD∥EF,
∴=,即=,
∴BC=,
∴CE=BE﹣BC=12﹣=.
故选:C.
6.解:∵DE∥BC,AD=6,BD=3,AE=4,
∴,
∴EC=2,
∴AC=2+4=6.
故选:C.
7.解:由题意得,A中三角形对应角相等,对应边成比例,两三角形相似;
C,D中正方形,菱形四条边均相等,所以对应边成比例,又角也相等,所以正方形,菱形相似;
而B中矩形四个角相等,但对应边不一定成比例,所以B中矩形不是相似多边形.
故选:B.
8.解:∵△ABC∽△ACD,相似比为2,
∴S△ABC:S△ACD=4,
∴S△BDC:S△ACD=3:1.
故选:B.
9.解:∵AB∥DE,
∴△CAB∽△CDE,
∴=,
而BC=BE,
∴DE=2AB=2×15=30(cm).
故选:D.
10.解:根据射影定理得:AB2=AD?AC,
∴AD==.
故选:A.
二.填空题
11.解:
∵△ABC是直角三角形,AD是斜边BC上的高,
∴AD2=BD?CD(射影定理),
∵BD=4,CD=9,
∴AD=6.
12.解:如图,过点DG作DG∥AE,交BE于点G;
∵AD是△ABC的中线,
∴DG=,
∵AC=2CE,
∴DG=AC,
∴=,
=,
即=5,
故答案为5.
13.解:∵∠A=50°,∠C=110°,
∴∠B=180°﹣50°﹣110°=20°,
∵△ABC∽△A′B′C′,
∴∠B′=∠B=20°.
故答案为20°.
14.解:∵△DEF与△ABC位似,点O为位似中心,
∴△DEF与△ABC的周长之比是:1:2.
故答案为:1:2.
15.解:∵BD⊥AB,AC⊥AB,
∴BD∥AC,
∴△ACE∽△BDE,
∴,
∴=,
∴AC=7(米),
故答案为:7.
16.解:∵∠A=∠A,
∴当∠ACP=∠B,或∠APC=∠ACB或=时,△ACP∽△ABC,
故答案为:∠ACP=∠B,或∠APC=∠ACB或=.
三.解答题
17.解:(1)∵AD∥BE∥CF,
∴=,即=,
∴DE=;
(2)∵OF=1,
∴OE=6﹣1=5,
∴OD=5+=,
∵AD∥CF,
∴===.
18.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴=,=,
∴=,
即CF2=GF?EF.
19.(1)解:△BEF≌△DAF,△BEF∽△GBF;
(2)证明:∵BE∥AC,
∴∠1=∠E,
在△BEF和△DAF中,
∵,
∴△BEF≌△DAF(AAS);
∵BE∥AC,
∴∠1=∠E,
∵∠1=∠2,
∴∠2=∠E,
又∵∠F为公共角,
∴△BEF∽△GBF.
20.解:(1)如图所示:△A1B1C1,即为所求,点A1的坐标为:(﹣3,2);
故答案为:(﹣3,2);
(2)如图所示:△A2B2C2,即为所求.
21.证明:(1)∵∠1=∠2,
∴∠1+∠CBE=∠2+∠CBE,即∠ABE=∠CBD,
在△ABE和△CBD中,
,
∴△ABE≌△CBD(SAS);
(2)∵△ABE≌△CBD,
∴∠A=∠C,
∵∠AFB=∠CFE,
∴∠1=∠3.
22.解:(1)∵AB?AM=AE?AC,
∴=,
∵∠CAB=∠CAB,
∴△ACB∽△AME,
∴∠AME=∠ACB,
由于∠AME+∠BAC=90°,
则∠ACB+∠BAC=90°,
∴?ABCD是矩形.
(2)由(1)可知:DE=EC,AE=EC,
∵ME⊥AC,
∴ME平分∠AMC,
∴∠CME=∠AME=∠ECB,
∵∠MEC=∠FEC=90°,
∴△CEF∽△MEC,
∴,
∴EC2=EF?EM,
即DE2=EF?EM
23.解:∵∠A是公共角,
∴当=,即=时,△ADE∽△ABC,
解得:DE=6;
当=,即=时,△ADE∽△ACB,
解得:DE=,
综上可得:当DE=6或时,△ADE与原三角形相似.
24.解:由题意得AP=4t,CQ=2t,则CP=20﹣4t,
(1)当t=3时,CP=20﹣4t=8cm,CQ=2t=6cm,
由勾股定理得PQ=;
(2)由题意得AP=4t,CQ=2t,则CP=20﹣4t,
因此Rt△CPQ的面积为S=cm2;
(3)分两种情况:
①当Rt△CPQ∽Rt△CAB时,,即,解得t=3;
②当Rt△CPQ∽Rt△CBA时,,即,解得t=.
因此t=3或t=时,以点C、P、Q为顶点的三角形与△ABC相似.
