人教版九年级数学下册《第27章 相似数》单元测试题(Word版 有答案)
文档属性
| 名称 | 人教版九年级数学下册《第27章 相似数》单元测试题(Word版 有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 432.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-26 00:00:00 | ||
图片预览

文档简介
人教版九年级数学下册《第27章
相似数》单元测试题
一.选择题(共10小题,每小题3分,满分30分)
1.若=,则的值为( )
A.5
B.
C.3
D.
2.已知=,则代数式的值为( )
A.
B.
C.
D.
3.以下各图放置的小正方形的边长都相同,分别以小正方形的顶点为顶点画三角形,则与△ABC相似的三角形图形为( )
A.
B.
C.
D.
4.如图,G,E分别是正方形ABCD的边AB,BC上的点,且AG=CE,AE⊥EF,AE=EF,如下结论:①BE=GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH,其中,正确的结论有( )
A.1个
B.2个
C.3个
D.4个
5.在△ABC中,点D、E分别在AB、AC上,如果AD=2,BD=3,那么由下列条件能够判定DE∥BC的是( )
A.=
B.=
C.=
D.=
6.如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则AC的长为( )
A.2
B.4
C.6
D.8
7.两个相似多边形的面积之比是1:4,则这两个相似多边形的周长之比是( )
A.1:2
B.1:4
C.1:8
D.1:16
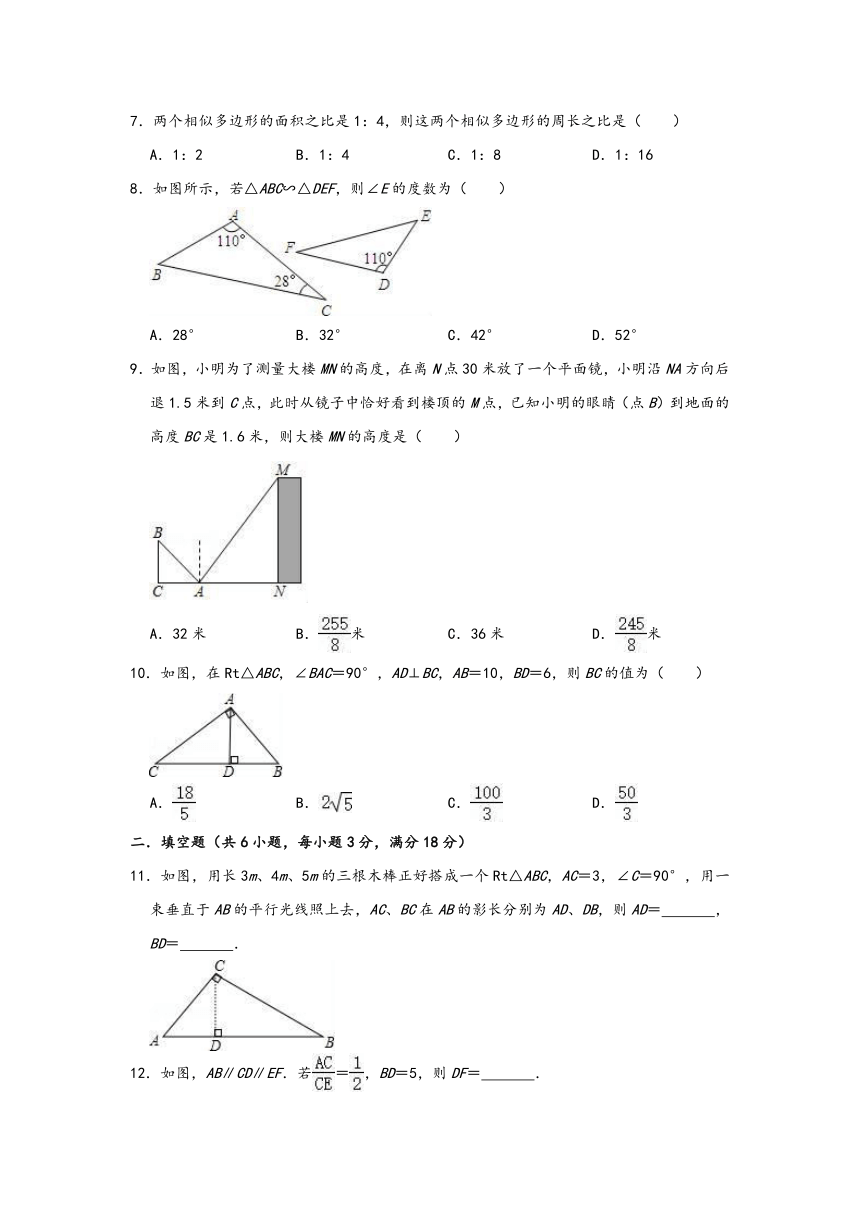
8.如图所示,若△ABC∽△DEF,则∠E的度数为( )
A.28°
B.32°
C.42°
D.52°
9.如图,小明为了测量大楼MN的高度,在离N点30米放了一个平面镜,小明沿NA方向后退1.5米到C点,此时从镜子中恰好看到楼顶的M点,已知小明的眼睛(点B)到地面的高度BC是1.6米,则大楼MN的高度是( )
A.32米
B.米
C.36米
D.米
10.如图,在Rt△ABC,∠BAC=90°,AD⊥BC,AB=10,BD=6,则BC的值为( )
A.
B.
C.
D.
二.填空题(共6小题,每小题3分,满分18分)
11.如图,用长3m、4m、5m的三根木棒正好搭成一个Rt△ABC,AC=3,∠C=90°,用一束垂直于AB的平行光线照上去,AC、BC在AB的影长分别为AD、DB,则AD=
,BD=
.
12.如图,AB∥CD∥EF.若=,BD=5,则DF=
.
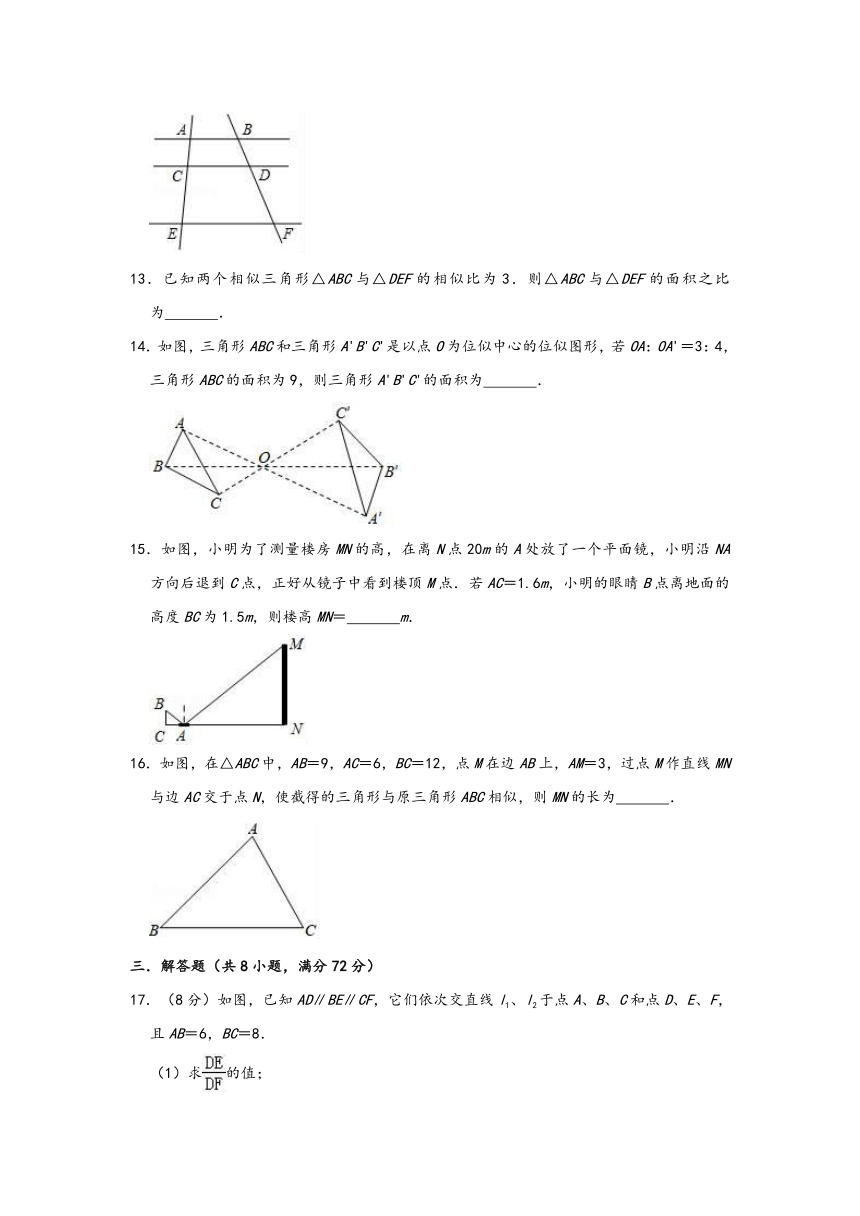
13.已知两个相似三角形△ABC与△DEF的相似比为3.则△ABC与△DEF的面积之比为
.
14.如图,三角形ABC和三角形A'B'C'是以点O为位似中心的位似图形,若OA:OA'=3:4,三角形ABC的面积为9,则三角形A'B'C'的面积为
.
15.如图,小明为了测量楼房MN的高,在离N点20m的A处放了一个平面镜,小明沿NA方向后退到C点,正好从镜子中看到楼顶M点.若AC=1.6m,小明的眼睛B点离地面的高度BC为1.5m,则楼高MN=
m.
16.如图,在△ABC中,AB=9,AC=6,BC=12,点M在边AB上,AM=3,过点M作直线MN与边AC交于点N,使截得的三角形与原三角形ABC相似,则MN的长为
.
三.解答题(共8小题,满分72分)
17.(8分)如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F,且AB=6,BC=8.
(1)求的值;
(2)当AD=5,CF=19时,求BE的长.
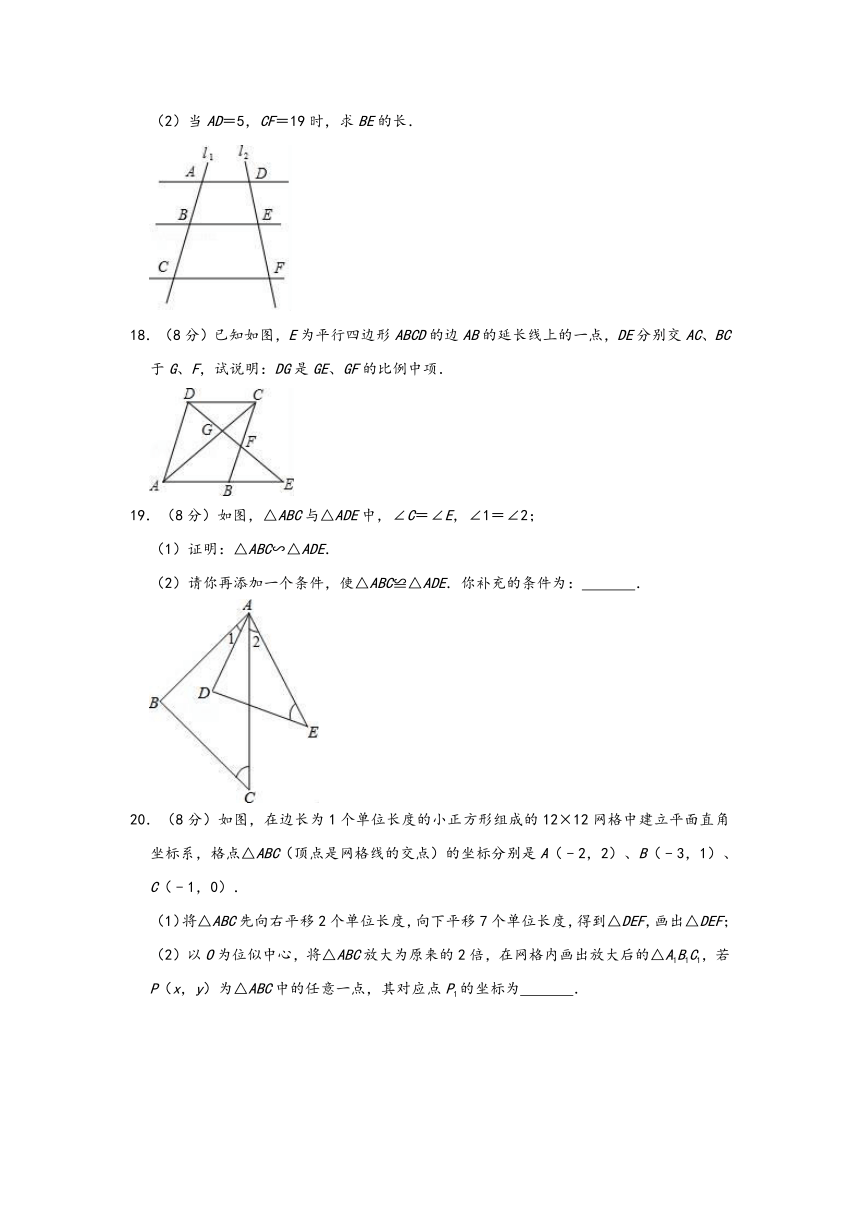
18.(8分)已知如图,E为平行四边形ABCD的边AB的延长线上的一点,DE分别交AC、BC于G、F,试说明:DG是GE、GF的比例中项.
19.(8分)如图,△ABC与△ADE中,∠C=∠E,∠1=∠2;
(1)证明:△ABC∽△ADE.
(2)请你再添加一个条件,使△ABC≌△ADE.你补充的条件为:
.
20.(8分)如图,在边长为1个单位长度的小正方形组成的12×12网格中建立平面直角坐标系,格点△ABC(顶点是网格线的交点)的坐标分别是A(﹣2,2)、B(﹣3,1)、C(﹣1,0).
(1)将△ABC先向右平移2个单位长度,向下平移7个单位长度,得到△DEF,画出△DEF;
(2)以O为位似中心,将△ABC放大为原来的2倍,在网格内画出放大后的△A1B1C1,若P(x,y)为△ABC中的任意一点,其对应点P1的坐标为
.
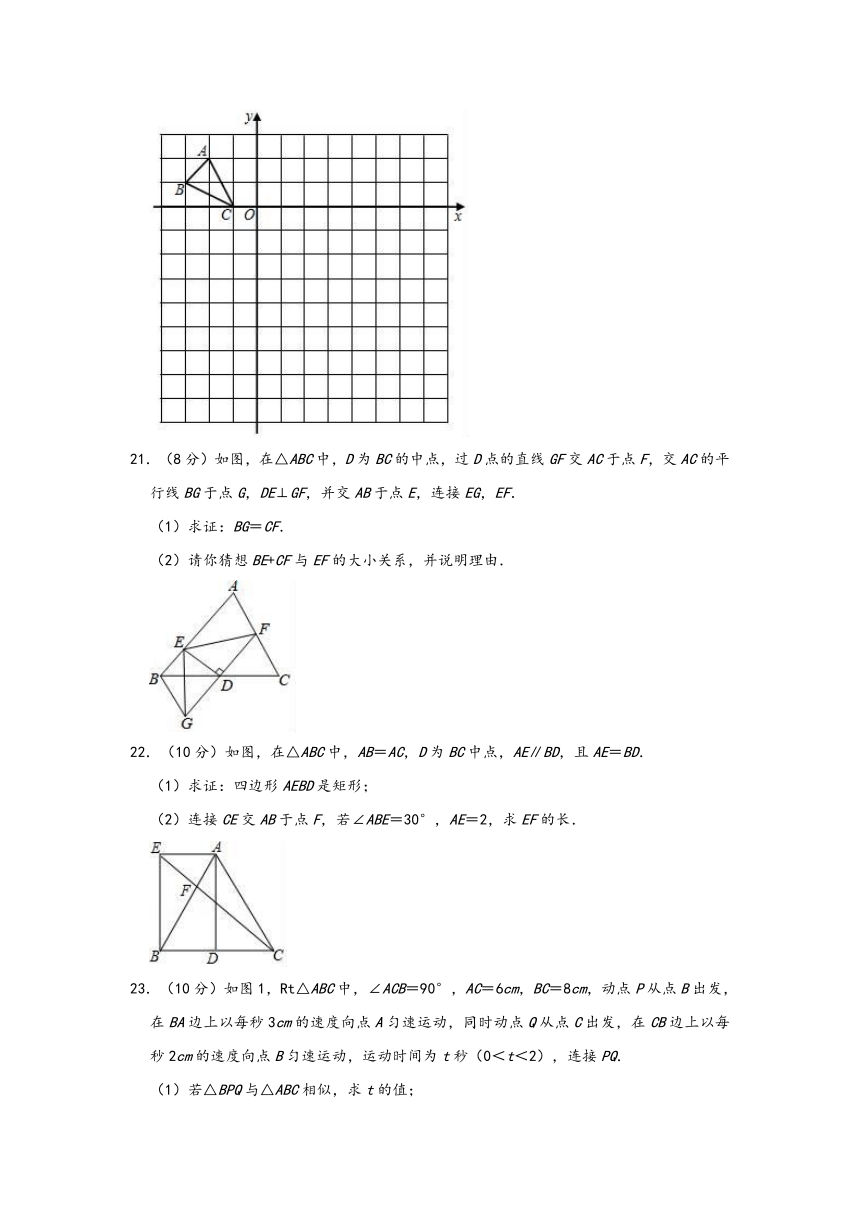
21.(8分)如图,在△ABC中,D为BC的中点,过D点的直线GF交AC于点F,交AC的平行线BG于点G,DE⊥GF,并交AB于点E,连接EG,EF.
(1)求证:BG=CF.
(2)请你猜想BE+CF与EF的大小关系,并说明理由.
22.(10分)如图,在△ABC中,AB=AC,D为BC中点,AE∥BD,且AE=BD.
(1)求证:四边形AEBD是矩形;
(2)连接CE交AB于点F,若∠ABE=30°,AE=2,求EF的长.
23.(10分)如图1,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒3cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒2cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)(如图2)连接AQ,CP,若AQ⊥CP,求t的值.
24.(12分)在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm.现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动.如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动,设运动的时间为t秒.
求:(1)用含t的代数式表示Rt△CPQ的面积S;
(2)当t=3时,P、Q两点之间的距离是多少?
(3)当t为多少时,以点C、P、Q为顶点的三角形与△ABC相似?
参考答案与试题解析
一.选择题
1.解:由=,得
4b=a﹣b.,解得a=5b,
==5,
故选:A.
2.解:由=得到:a=b,则
==.
故选:B.
3.解:设每个小正方形的边长为1,则△ABC的各边长分别为:2,,,同理求得:
A中三角形的各边长为:,1,,与△ABC的各边对应成比例,所以两三角形相似;
故选:A.
4.解:∵四边形ABCD是正方形,
∴∠B=∠DCB=90°,AB=BC,
∵AG=CE,
∴BG=BE,
由勾股定理得:BE=GE,∴①正确;
∵BG=BE,∠B=90°,
∴∠BGE=∠BEG=45°,
∴∠AGE=135°,
∴∠GAE+∠AEG=45°,
∵AE⊥EF,
∴∠AEF=90°,
∵∠BEG=45°,
∴∠AEG+∠FEC=45°,
∴∠GAE=∠FEC,
在△GAE和△CEF中
∴△AGE≌△ECF,∴②正确;
∴∠AGE=∠ECF=135°,
∴∠FCD=135°﹣90°=45°,∴③正确;
∵∠BGE=∠BEG=45°,∠AEG+∠FEC=45°,
∴∠FEC<45°,
∴△GBE和△ECH不相似,∴④错误;
即正确的有3个.
故选:C.
5.解:当=或=时,DE∥BD,
即=或=.
故选:D.
6.解:∵DE∥BC,
∴,即,
解得:EC=2,
∴AC=AE+EC=4+2=6;
故选:C.
7.解:∵两个相似多边形的面积之比是1:4,
∴这两个相似多边形的相似比是1:2,
则这两个相似多边形的周长之比是1:2,
故选:A.
8.解:∵∠A=110°,∠C=28°,
∴∠B=42°,
∵△ABC∽△DEF,
∴∠B=∠E.
∴∠E=42°.
故选:C.
9.解:∵BC⊥CA,MN⊥AN,
∴∠C=∠MNA=90°,
∵∠BAC=∠MAN,
∴△BCA∽△MNA.
∴=,
即=,
∴MN=32(m),
答:楼房MN的高度为32m.
故选:A.
10.解:根据射影定理得:AB2=BD×BC,
∴BC==.
故选:D.
二.填空题
11.解:依题意知,AC=3cm,AB=5cm,BC=4cm,∠C=90°.
∵CD⊥AB,
∴AC2=AD?AB,BC2=BD?AB,
则9=5AD,16=5BD,
所以AD=,BD=.
故答案是:;.
12.解:∵AB∥CD∥EF,
∴==,
∴DF=2BD=2×5=10.
故答案为10.
13.解:∵△ABC与△DEF的相似比为3,
∴△ABC与△DEF的面积之比为9.
故答案为9.
14.解:∵三角形ABC和三角形A'B'C'是以点O为位似中心的位似图形,OA:OA'=3:4,
∴AC:A′C′=OA:OA′=3:4,
∵三角形ABC的面积为9,
∴三角形A'B'C'的面积为:16.
故答案为:16.
15.解:∵BC⊥CA,MN⊥AN,
∴∠C=∠N=90°,
∵∠BAC=∠MAN,
∴△BCA∽△MNA.
∴,
即,
∴MN=(m),
答:楼房MN的高度为m,
故答案为:.
16.解:∵△AMN和△ABC相似,
∴①如图1,△AMN∽△ABC,
∴,
∵AM=3,AC=6,BC=12,AB=9,
∴,MN=4.
②如图2,△AMN∽△ACB,
∴,
∵AM=3,AC=6,BC=12,
∴,MN=6,
综上MN为4或6.
故答案为:4或6.
三.解答题
17.解:(1)∵AD∥BE∥CF,
∴===;
(2)过D点作DM∥AC交CF于M,交BE于N,如图,
∵AD∥BN∥CM,AC∥DM,
∴四边形ABND和四边形ACMD都是平行四边形,
∴BN=AD=5,CM=AD=5,
∴MF=CF﹣CM=19﹣5=14,
∵NF∥MF,
∴==,
∴NE=MF=×14=6,
∴BE=BN+NE=5+6=11.
18.解:∵四边形ABCD是平行四边形,
∴DC∥AE,
∴=,
∵AD∥BC,
∴=,
∴=,
∴DG2=GE?GF,
∴DG是GE、GF的比例中项.
19.(1)证明:∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
∴∠BAC=∠DAE.
∵∠C=∠E,
∴△ABC∽△ADE.
(2)补充的条件为:AB=AD(答案不唯一);理由如下:
由(1)得:∠BAC=∠DAE,
在△ABC和△ADE中,,
∴△ABC≌△ADE;
故答案为:AB=AD(答案不唯一).
20.解:(1)如图所示:△DEF即为所求;
(2)如图所示:△A1B1C1即为所求,若P(x,y)为△ABC中的任意一点,
其对应点P1的坐标为:(﹣2x,﹣2y).
21.(1)证明:∵BG∥AC,
∴∠C=∠GBD,
∵D是BC的中点,
∴BD=DC,
在△CFD和△BGD中
,
∴△CFD≌△BGD,
∴BG=CF.
(2)BE+CF>EF,
理由如下:
∵△CFD≌△BGD,
∴CF=BG,
在△BGE中,BG+BE>EG,
∵△CFD≌△BGD,
∴GD=DF,ED⊥GF,
∴EF=EG,
∴BG+CF>EF.
22.(1)证明:∵AE∥BD,AE=BD,
∴四边形AEBD是平行四边形,
∵AB=AC,D为BC的中点,
∴AD⊥BC,
∴∠ADB=90°,
∴四边形AEBD是矩形.
(2)解:∵四边形AEBD是矩形,
∴∠AEB=90°,
∵∠ABE=30°,AE=2,
∴BE=2,BC=4,
∴EC=2,
∵AE∥BC,
∴△AEF∽△BCF,
∴==,
∴EF=EC=.
23.解:(1)①当△BPQ∽△BAC时,
∵,BP=3t,QC=2t,AB=10cm,BC=8cm,
∴,
∴,
②当△BPQ∽△BCA时,
∵,
∴,
∴;
∴或时,△BPQ与△ABC相似;
(2)如图所示,过P作PM⊥BC于点M,AQ,CP交于点N,
则有PB=3t,,,,
∵∠NAC+∠NCA=90°,∠PCM+∠NCA=90°,
∴∠NAC=∠PCM且∠ACQ=∠PMC=90°,
∴△ACQ∽△CMP,
∴,
∴
解得:;
24.解:(1)由题意得AP=4t,CQ=2t,则CP=20﹣4t,
因此Rt△CPQ的面积为S=cm2;
(2)当t=3时,CP=20﹣4t=8cm,CQ=2t=6cm,
由勾股定理得PQ=;
(3)分两种情况:
①当Rt△CPQ∽Rt△CAB时,,即,解得t=3;
②当Rt△CPQ∽Rt△CBA时,,即,解得t=.
因此t=3或t=时,以点C、P、Q为顶点的三角形与△ABC相似.
相似数》单元测试题
一.选择题(共10小题,每小题3分,满分30分)
1.若=,则的值为( )
A.5
B.
C.3
D.
2.已知=,则代数式的值为( )
A.
B.
C.
D.
3.以下各图放置的小正方形的边长都相同,分别以小正方形的顶点为顶点画三角形,则与△ABC相似的三角形图形为( )
A.
B.
C.
D.
4.如图,G,E分别是正方形ABCD的边AB,BC上的点,且AG=CE,AE⊥EF,AE=EF,如下结论:①BE=GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH,其中,正确的结论有( )
A.1个
B.2个
C.3个
D.4个
5.在△ABC中,点D、E分别在AB、AC上,如果AD=2,BD=3,那么由下列条件能够判定DE∥BC的是( )
A.=
B.=
C.=
D.=
6.如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则AC的长为( )
A.2
B.4
C.6
D.8
7.两个相似多边形的面积之比是1:4,则这两个相似多边形的周长之比是( )
A.1:2
B.1:4
C.1:8
D.1:16
8.如图所示,若△ABC∽△DEF,则∠E的度数为( )
A.28°
B.32°
C.42°
D.52°
9.如图,小明为了测量大楼MN的高度,在离N点30米放了一个平面镜,小明沿NA方向后退1.5米到C点,此时从镜子中恰好看到楼顶的M点,已知小明的眼睛(点B)到地面的高度BC是1.6米,则大楼MN的高度是( )
A.32米
B.米
C.36米
D.米
10.如图,在Rt△ABC,∠BAC=90°,AD⊥BC,AB=10,BD=6,则BC的值为( )
A.
B.
C.
D.
二.填空题(共6小题,每小题3分,满分18分)
11.如图,用长3m、4m、5m的三根木棒正好搭成一个Rt△ABC,AC=3,∠C=90°,用一束垂直于AB的平行光线照上去,AC、BC在AB的影长分别为AD、DB,则AD=
,BD=
.
12.如图,AB∥CD∥EF.若=,BD=5,则DF=
.
13.已知两个相似三角形△ABC与△DEF的相似比为3.则△ABC与△DEF的面积之比为
.
14.如图,三角形ABC和三角形A'B'C'是以点O为位似中心的位似图形,若OA:OA'=3:4,三角形ABC的面积为9,则三角形A'B'C'的面积为
.
15.如图,小明为了测量楼房MN的高,在离N点20m的A处放了一个平面镜,小明沿NA方向后退到C点,正好从镜子中看到楼顶M点.若AC=1.6m,小明的眼睛B点离地面的高度BC为1.5m,则楼高MN=
m.
16.如图,在△ABC中,AB=9,AC=6,BC=12,点M在边AB上,AM=3,过点M作直线MN与边AC交于点N,使截得的三角形与原三角形ABC相似,则MN的长为
.
三.解答题(共8小题,满分72分)
17.(8分)如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F,且AB=6,BC=8.
(1)求的值;
(2)当AD=5,CF=19时,求BE的长.
18.(8分)已知如图,E为平行四边形ABCD的边AB的延长线上的一点,DE分别交AC、BC于G、F,试说明:DG是GE、GF的比例中项.
19.(8分)如图,△ABC与△ADE中,∠C=∠E,∠1=∠2;
(1)证明:△ABC∽△ADE.
(2)请你再添加一个条件,使△ABC≌△ADE.你补充的条件为:
.
20.(8分)如图,在边长为1个单位长度的小正方形组成的12×12网格中建立平面直角坐标系,格点△ABC(顶点是网格线的交点)的坐标分别是A(﹣2,2)、B(﹣3,1)、C(﹣1,0).
(1)将△ABC先向右平移2个单位长度,向下平移7个单位长度,得到△DEF,画出△DEF;
(2)以O为位似中心,将△ABC放大为原来的2倍,在网格内画出放大后的△A1B1C1,若P(x,y)为△ABC中的任意一点,其对应点P1的坐标为
.
21.(8分)如图,在△ABC中,D为BC的中点,过D点的直线GF交AC于点F,交AC的平行线BG于点G,DE⊥GF,并交AB于点E,连接EG,EF.
(1)求证:BG=CF.
(2)请你猜想BE+CF与EF的大小关系,并说明理由.
22.(10分)如图,在△ABC中,AB=AC,D为BC中点,AE∥BD,且AE=BD.
(1)求证:四边形AEBD是矩形;
(2)连接CE交AB于点F,若∠ABE=30°,AE=2,求EF的长.
23.(10分)如图1,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒3cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒2cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)(如图2)连接AQ,CP,若AQ⊥CP,求t的值.
24.(12分)在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm.现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动.如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动,设运动的时间为t秒.
求:(1)用含t的代数式表示Rt△CPQ的面积S;
(2)当t=3时,P、Q两点之间的距离是多少?
(3)当t为多少时,以点C、P、Q为顶点的三角形与△ABC相似?
参考答案与试题解析
一.选择题
1.解:由=,得
4b=a﹣b.,解得a=5b,
==5,
故选:A.
2.解:由=得到:a=b,则
==.
故选:B.
3.解:设每个小正方形的边长为1,则△ABC的各边长分别为:2,,,同理求得:
A中三角形的各边长为:,1,,与△ABC的各边对应成比例,所以两三角形相似;
故选:A.
4.解:∵四边形ABCD是正方形,
∴∠B=∠DCB=90°,AB=BC,
∵AG=CE,
∴BG=BE,
由勾股定理得:BE=GE,∴①正确;
∵BG=BE,∠B=90°,
∴∠BGE=∠BEG=45°,
∴∠AGE=135°,
∴∠GAE+∠AEG=45°,
∵AE⊥EF,
∴∠AEF=90°,
∵∠BEG=45°,
∴∠AEG+∠FEC=45°,
∴∠GAE=∠FEC,
在△GAE和△CEF中
∴△AGE≌△ECF,∴②正确;
∴∠AGE=∠ECF=135°,
∴∠FCD=135°﹣90°=45°,∴③正确;
∵∠BGE=∠BEG=45°,∠AEG+∠FEC=45°,
∴∠FEC<45°,
∴△GBE和△ECH不相似,∴④错误;
即正确的有3个.
故选:C.
5.解:当=或=时,DE∥BD,
即=或=.
故选:D.
6.解:∵DE∥BC,
∴,即,
解得:EC=2,
∴AC=AE+EC=4+2=6;
故选:C.
7.解:∵两个相似多边形的面积之比是1:4,
∴这两个相似多边形的相似比是1:2,
则这两个相似多边形的周长之比是1:2,
故选:A.
8.解:∵∠A=110°,∠C=28°,
∴∠B=42°,
∵△ABC∽△DEF,
∴∠B=∠E.
∴∠E=42°.
故选:C.
9.解:∵BC⊥CA,MN⊥AN,
∴∠C=∠MNA=90°,
∵∠BAC=∠MAN,
∴△BCA∽△MNA.
∴=,
即=,
∴MN=32(m),
答:楼房MN的高度为32m.
故选:A.
10.解:根据射影定理得:AB2=BD×BC,
∴BC==.
故选:D.
二.填空题
11.解:依题意知,AC=3cm,AB=5cm,BC=4cm,∠C=90°.
∵CD⊥AB,
∴AC2=AD?AB,BC2=BD?AB,
则9=5AD,16=5BD,
所以AD=,BD=.
故答案是:;.
12.解:∵AB∥CD∥EF,
∴==,
∴DF=2BD=2×5=10.
故答案为10.
13.解:∵△ABC与△DEF的相似比为3,
∴△ABC与△DEF的面积之比为9.
故答案为9.
14.解:∵三角形ABC和三角形A'B'C'是以点O为位似中心的位似图形,OA:OA'=3:4,
∴AC:A′C′=OA:OA′=3:4,
∵三角形ABC的面积为9,
∴三角形A'B'C'的面积为:16.
故答案为:16.
15.解:∵BC⊥CA,MN⊥AN,
∴∠C=∠N=90°,
∵∠BAC=∠MAN,
∴△BCA∽△MNA.
∴,
即,
∴MN=(m),
答:楼房MN的高度为m,
故答案为:.
16.解:∵△AMN和△ABC相似,
∴①如图1,△AMN∽△ABC,
∴,
∵AM=3,AC=6,BC=12,AB=9,
∴,MN=4.
②如图2,△AMN∽△ACB,
∴,
∵AM=3,AC=6,BC=12,
∴,MN=6,
综上MN为4或6.
故答案为:4或6.
三.解答题
17.解:(1)∵AD∥BE∥CF,
∴===;
(2)过D点作DM∥AC交CF于M,交BE于N,如图,
∵AD∥BN∥CM,AC∥DM,
∴四边形ABND和四边形ACMD都是平行四边形,
∴BN=AD=5,CM=AD=5,
∴MF=CF﹣CM=19﹣5=14,
∵NF∥MF,
∴==,
∴NE=MF=×14=6,
∴BE=BN+NE=5+6=11.
18.解:∵四边形ABCD是平行四边形,
∴DC∥AE,
∴=,
∵AD∥BC,
∴=,
∴=,
∴DG2=GE?GF,
∴DG是GE、GF的比例中项.
19.(1)证明:∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
∴∠BAC=∠DAE.
∵∠C=∠E,
∴△ABC∽△ADE.
(2)补充的条件为:AB=AD(答案不唯一);理由如下:
由(1)得:∠BAC=∠DAE,
在△ABC和△ADE中,,
∴△ABC≌△ADE;
故答案为:AB=AD(答案不唯一).
20.解:(1)如图所示:△DEF即为所求;
(2)如图所示:△A1B1C1即为所求,若P(x,y)为△ABC中的任意一点,
其对应点P1的坐标为:(﹣2x,﹣2y).
21.(1)证明:∵BG∥AC,
∴∠C=∠GBD,
∵D是BC的中点,
∴BD=DC,
在△CFD和△BGD中
,
∴△CFD≌△BGD,
∴BG=CF.
(2)BE+CF>EF,
理由如下:
∵△CFD≌△BGD,
∴CF=BG,
在△BGE中,BG+BE>EG,
∵△CFD≌△BGD,
∴GD=DF,ED⊥GF,
∴EF=EG,
∴BG+CF>EF.
22.(1)证明:∵AE∥BD,AE=BD,
∴四边形AEBD是平行四边形,
∵AB=AC,D为BC的中点,
∴AD⊥BC,
∴∠ADB=90°,
∴四边形AEBD是矩形.
(2)解:∵四边形AEBD是矩形,
∴∠AEB=90°,
∵∠ABE=30°,AE=2,
∴BE=2,BC=4,
∴EC=2,
∵AE∥BC,
∴△AEF∽△BCF,
∴==,
∴EF=EC=.
23.解:(1)①当△BPQ∽△BAC时,
∵,BP=3t,QC=2t,AB=10cm,BC=8cm,
∴,
∴,
②当△BPQ∽△BCA时,
∵,
∴,
∴;
∴或时,△BPQ与△ABC相似;
(2)如图所示,过P作PM⊥BC于点M,AQ,CP交于点N,
则有PB=3t,,,,
∵∠NAC+∠NCA=90°,∠PCM+∠NCA=90°,
∴∠NAC=∠PCM且∠ACQ=∠PMC=90°,
∴△ACQ∽△CMP,
∴,
∴
解得:;
24.解:(1)由题意得AP=4t,CQ=2t,则CP=20﹣4t,
因此Rt△CPQ的面积为S=cm2;
(2)当t=3时,CP=20﹣4t=8cm,CQ=2t=6cm,
由勾股定理得PQ=;
(3)分两种情况:
①当Rt△CPQ∽Rt△CAB时,,即,解得t=3;
②当Rt△CPQ∽Rt△CBA时,,即,解得t=.
因此t=3或t=时,以点C、P、Q为顶点的三角形与△ABC相似.
