2020-2021学年湘教版九年级下册数学《第2章 圆》单元测试卷(word版含解析)
文档属性
| 名称 | 2020-2021学年湘教版九年级下册数学《第2章 圆》单元测试卷(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 306.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-28 08:53:30 | ||
图片预览



文档简介
2020-2021学年湘教新版九年级下册数学《第2章 圆》单元测试卷
一.选择题
1.把圆的半径缩小到原来的,那么圆的面积缩小到原来的( )
A. B. C. D.
2.如图,D是的中点,则图中与∠ABD相等的角的个数是( )
A.4个 B.3个 C.2个 D.1个
3.如图,点C在线段AB上,以AB、AC为直径的半圆相切于点A,大圆的弦AE交小圆于点D,∠EAB=α,如DE=2,那么BC等于( )
A.2cosα B.2sinα C. D.
4.在圆柱形油槽内装有一些油,截面如图,油面宽AB为6dm,如果再注入一些油后,油面AB上升1dm,油面宽为8dm,圆柱形油槽直径MN为( )
A.6dm B.8dm C.10dm D.12dm
5.已知⊙O的半径为1,点P到O的距离为R,且方程x2﹣2x+R=0有实数根,则P( )
A.在⊙O的内部 B.在⊙O上
C.在⊙O外部 D.在⊙O的内部或圆上
6.已知在△ABC中,∠A:∠B:∠C=1:2:3,以B为圆心,BC为半径的⊙B与AC边的位置关系是( )
A.相离 B.相切 C.相交 D.不确定
7.在下列各结论中,正确的为( )
A.圆心角相等的两个扇形相同
B.圆心角相等的两个扇形的面积相等
C.两个面积相等的扇形的圆心角相等
D.同圆或等圆中面积相等的两个扇形的圆心角相等
8.在平行四边形、矩形、正方形、菱形、等腰梯形、直角梯形中,必定存在外接圆的有( )
A.1个 B.2个 C.3个 D.4个
9.下列命题中,真命题的个数为( )
①任意三点确定一个圆;②平分弦的直径垂直于弦;③90°的圆周角所对的弦是直径;④同弧或等弧所对的圆周角相等.
A.1个 B.2个 C.3个 D.4个
10.如图,PA=PB,OE⊥PA,OF⊥PB,则以下结论:①OP是∠APB的平分线;②PE=PF③CA=BD;④CD∥AB;其中正确的有( )个.
A.4 B.3 C.2 D.1
二.填空题
11.各边相等的圆内接多边形 正多边形;各角相等的圆内接多边形 正多边形.(填“是”或“不是”)
12.⊙O半径为3,圆心O到直线L的距离为d,若直线L与⊙O相交,则d的取值范围是 .
13.如图,⊙O是△ABC的外接圆,∠A=45°,BC=3,则⊙O的直径为 .
14.如果⊙O的半径为r,点P到圆心O的距离为d,那么:①点P在⊙O外,则 ;② ,则d=r;③ ,则d<r.
15.如图,△ABC内接于⊙O,D是劣弧弧AB上的一点,E是BC延长线上一点,AE交⊙O于F,为使△ADB∽△ACE,应补充的一个条件是 或 .
16.扇形的圆心角度数60°,面积6π,则扇形的弧长为 .
17.一个三角形的外心与内心恰好重合,这个三角形是 .
18.如图,EB、EC是⊙O的两条切线,B、C为切点,A是⊙O上的任意一点,若∠A=70°,则∠E= .
19.如图,水平放着的圆柱形排水管的截面为1000mm,其中水面宽AB=800mm,则水的最大深度为 mm.
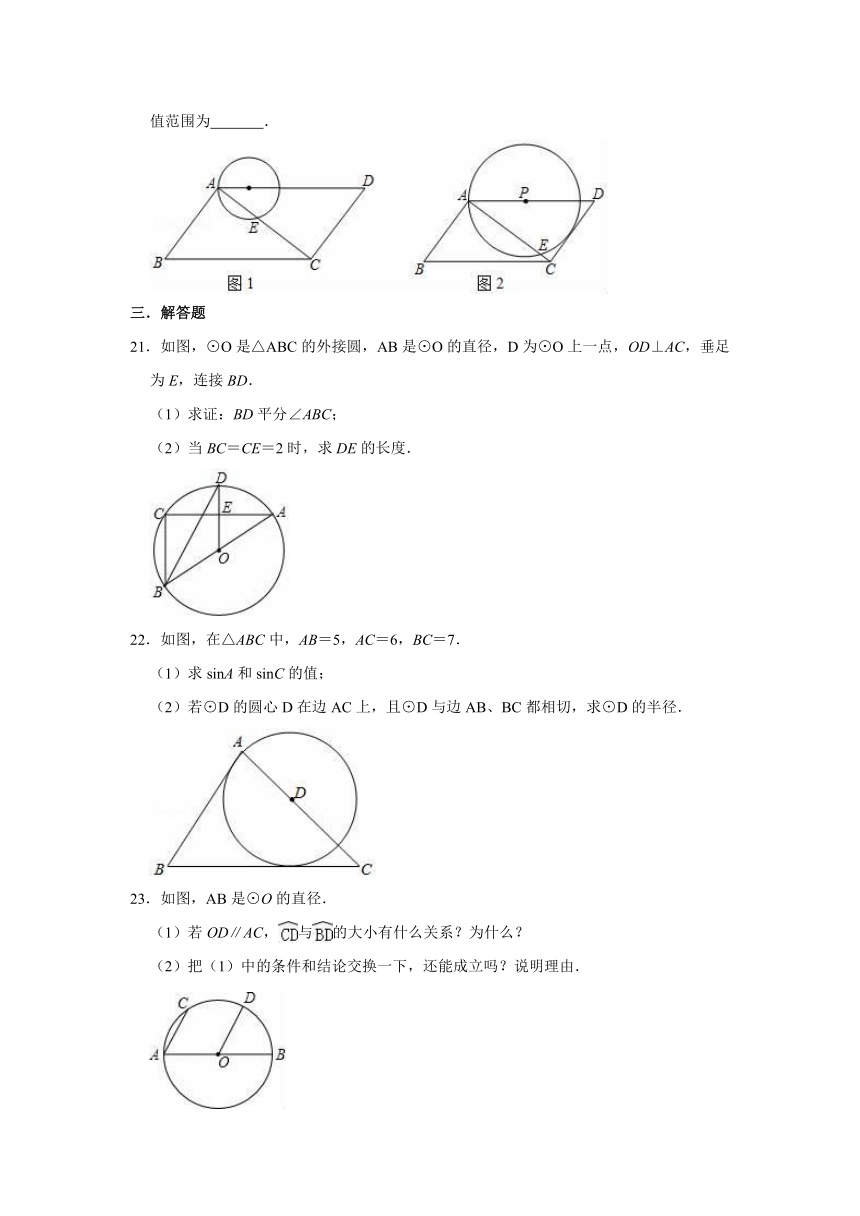
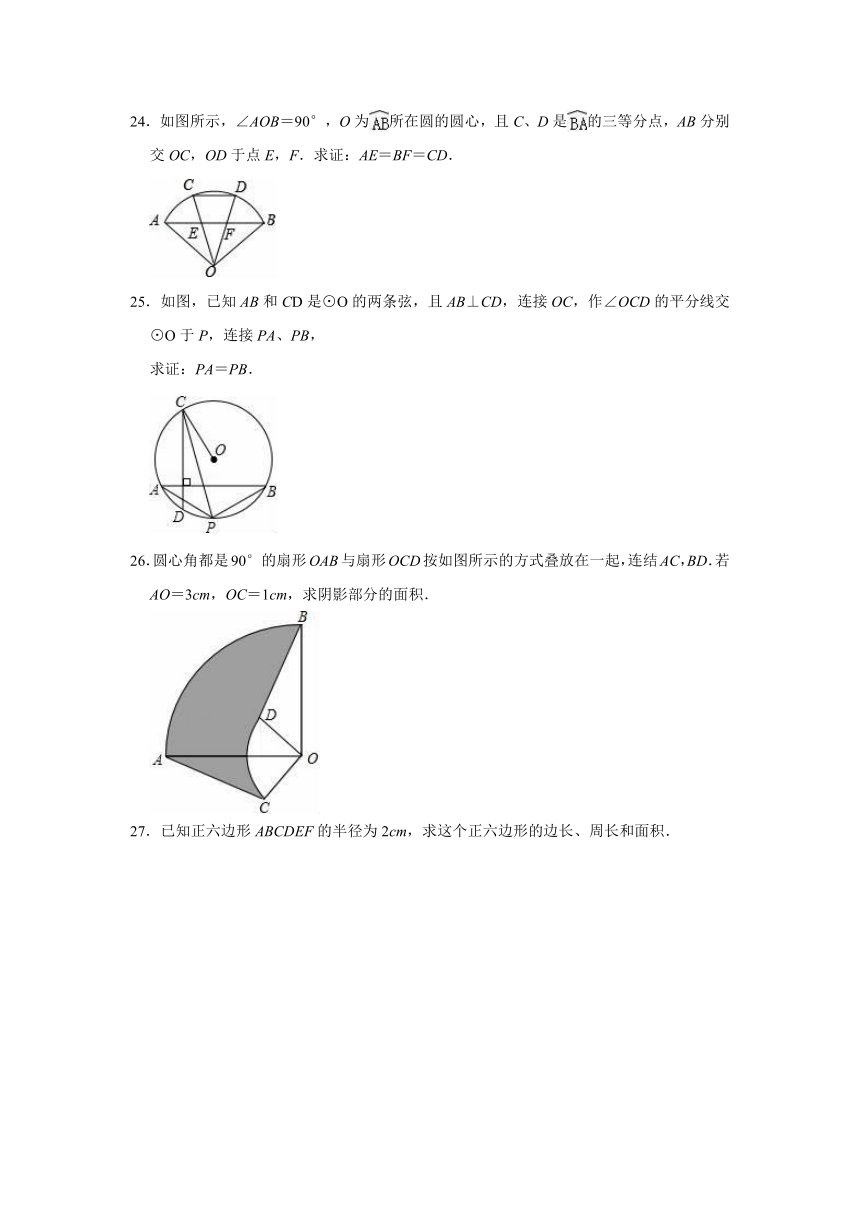
20.如图1,平行四边形ABCD中,AB⊥AC,AB=6,AD=10,点P在边AD上运动,以P为圆心,PA为半径的⊙P与对角线AC交于A,E两点.不难发现,随着AP的变化,⊙P与平行四边形ABCD的边的公共点的个数也在变化.如图2,当⊙P与边CD相切时,⊙P与平行四边形ABCD的边有三个公共点.若公共点的个数为4,则相对应的AP的取值范围为 .
三.解答题
21.如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.
(1)求证:BD平分∠ABC;
(2)当BC=CE=2时,求DE的长度.
22.如图,在△ABC中,AB=5,AC=6,BC=7.
(1)求sinA和sinC的值;
(2)若⊙D的圆心D在边AC上,且⊙D与边AB、BC都相切,求⊙D的半径.
23.如图,AB是⊙O的直径.
(1)若OD∥AC,与的大小有什么关系?为什么?
(2)把(1)中的条件和结论交换一下,还能成立吗?说明理由.
24.如图所示,∠AOB=90°,O为所在圆的圆心,且C、D是的三等分点,AB分别交OC,OD于点E,F.求证:AE=BF=CD.
25.如图,已知AB和CD是⊙O的两条弦,且AB⊥CD,连接OC,作∠OCD的平分线交⊙O于P,连接PA、PB,
求证:PA=PB.
26.圆心角都是90°的扇形OAB与扇形OCD按如图所示的方式叠放在一起,连结AC,BD.若AO=3cm,OC=1cm,求阴影部分的面积.
27.已知正六边形ABCDEF的半径为2cm,求这个正六边形的边长、周长和面积.
参考答案与试题解析
一.选择题
1.解:设原来的圆的半径为r,则面积s1=πr2,
∴缩小到原来的后,s2=π(r)2=πr2,
∴==.
故选:D.
2.解:∵D是的中点,
∴弧AD=弧CD,
∴∠ABD=∠CBD=∠ACD=∠DAC.
故选:B.
3.解:连接CD、BE,过C点作CF∥AE交BE于点F,
点C在线段AB上,AB、AC为直径,
所以有DC⊥AE,BE⊥AE,
即得CD∥BE,且四边形DCFE为正方形,
即FC=DE=2,∠FCB=∠EAB=α,
在Rt△BCF中,BC=
故选:C.
4.解:根据题意画出图形,如图所示,EF=1dm,AB=6dm,CD=8dm,设圆的半径为r,
∵OE⊥CD,OF⊥AB,
∴CE=DE=4dm,AF=BF=3dm,
在Rt△OCE和△OAF中,
根据勾股定理得:OE==,OF==,
∴OE﹣OF=1,即﹣=1,
=+1,
两边平方得,r2﹣9=r2﹣16+2+1,
=3,
两边平方得,r2﹣16=9,
r2=25,
解得:r=5,
则圆柱形油槽直径MN为10dm.
故选:C.
5.解:因为方程有实数根,所以△=4﹣4R≥0,得到R≤1,
而圆的半径为1,说明点P到圆心的距离小于或等于半径,所以点P在圆内或圆上.
故选:D.
6.解:∵在△ABC中,∠A:∠B:∠C=1:2:3,
∴∠A=30°,∠B=60°,∠C=90°,
∴以B为圆心,BC为半径的⊙B与AC边的位置关系是相切.
故选:B.
7.解:因为不是在同一个圆中的扇形面积和圆心角都无法比较,
故可以排除A,B,C 而对于同一个圆中,
扇形的面积为:s=lα2,
其中l为圆的半径,α为圆心角
故选:D.
8.解:根据圆内接多边形的性质可得:矩形,正方形与等腰梯形必定存在外接圆.故选C.
9.解:①假命题,当三点在同一条直线上时,就不能确定一个圆了;
②假命题,当弦为直径时就不一定垂直了;
③真命题;
④真命题,同弧或等弧所对的圆周角相等.
故选:B.
10.解:
连接OP、OC、OA、OD、OB、CD、AB.
∵PC?PA=PD?PB(相交弦定理),PA=PB(已知),
∴PC=PD,
∴AC=BD;
在△AOC和△BOD中,
∵∠AOC=∠BOD(等弦对等角),
OA=OB(半径),
OD=OC(半径),
∴△AOC≌△BOD,
∴③CA=BD;
OE=OF;
又∵OE⊥PA,OF⊥PB,
∴①OP是∠APB的平分线;
∴②PE=PF;
在△PCD和△PAB中,
PC:PA=PD:PB,
∠DPC=∠BPA,
∴△PCD∽△PAB,
∴∠PDC=PBA,
∴④CD∥AB;
综上所述,①②③④均正确,故答案选A.
二.填空题
11.解:∵正多边形的各边相等,
∴各边所对的圆周角必然相等,
∴各边相等的圆内接多边形是正多边形;
∵圆内接多边形的各角相等;
举出一个反例:当四个角都是直角时,这个四边形可能是矩形,
∴各角相等的圆内接多边形不一定是正多边形.
故答案为:是,不是.
12.解:∵直线和圆相交,
∴d<r.
又∵d是直线到圆心的距离,⊙O半径为3,
∴d是非负数,
∴0≤d<3.
13.解:连接OB、OC,如图,
∵∠BOC=2∠A=90°,
而OB=OC,
∴△OBC为等腰直角三角形,
∴OB=BC=,
∴⊙O的直径为3.
故答案为3.
14.解:①∵点P在⊙O外,∴d>r;故填:d>r.
②∵d=r,∴点在圆上;故填:点P在⊙O上.
③∵d<r,∴点在圆内;故填:点P在⊙O内.
15.解:∵四边形ADBC是⊙O的内接四边形,
∴∠ACE=∠D,∴当∠BAD=∠EAC或∠ABD=∠E时,△ADB∽△ACE.
16.解:6π=,
解得r=6,
弧长==2π.
17.解:根据等边三角形的性质可知,一个三角形的外心与内心恰好重合,这个三角形是等边三角形.
18.解:连接OB,OC.
则∠BOC=2∠A=2×70=140°,
∵EB、EC是⊙O的两条切线,
∴∠EBO=∠ECO=90°,
∴∠E=360°﹣∠BOC﹣∠EBO﹣∠ECO=360°﹣140°﹣90°﹣90°=40°.
故答案是:40°.
19.解:过O点作OC⊥AB,C为垂足,交⊙O于D,连OA,如图,
OA=500mm,AB=800mm,
∵OC⊥AB,
∴AC=BC=400mm,
在Rt△AOC中,OA2=AC2+OC2,
∴OC==300,
∴CD=300+500=800(mm),
即水的最大深度为800mm.
故答案为800mm.
20.解:∵平行四边形ABCD中,AB=6,AD=10,
∴BC=AD=10,
∵AB⊥AC,
∴在Rt△ABC中,由勾股定理得:AC===8,
如图2所示,连接PF,
设AP=x,则DP=10﹣x,PF=x,
∵⊙P与边CD相切于点F,
∴PF⊥CD,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AB⊥AC,
∴AC⊥CD,
∴AC∥PF,
∴△DPF∽△DAC,
∴=,
∴=,
∴x=,
即AP=;
当⊙P与BC相切时,设切点为G,如图3,
S?ABCD=×6×8×2=10PG,
∴PG=,
①当⊙P与边AD、CD分别有两个公共点时,<AP<,即此时⊙P与平行四边形ABCD的边的公共点的个数为4;
②⊙P过点A、C、D三点,如图4,⊙P与平行四边形ABCD的边的公共点的个数为4,此时AP=5,
综上所述,AP的值的取值范围是:<AP<或AP=5,
故答案为:<AP<或AP=5.
三.解答题
21.(1)证明:∵OD⊥AC,
∴=,
∴∠ABD=∠CBD,
∴BD平分∠ABC;
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵OD⊥AC,
∴AE=CE=2,
在Rt△ABC中,AB==2,
∴OD=,
∵AE=CE,OA=OB,
∴OE为△ABC的中位线,
∴OE=BC=1,
∴DE=﹣1.
22.解:(1)作BH⊥AC于H,如图,
设AH=x,则CH=6﹣x,
在Rt△ABH中,BH2+x2=52,
在Rt△CBH中,BH2+(6﹣x)2=72,
解得x=1,BH=2,
在Rt△ABH中,sinA==;
在Rt△CBH中,sinC==;
即sinA=,sinC=;
(2)作DE⊥AB于E,DF⊥BC于F,如图,设⊙D的半径为r,
∵⊙D与边AB、BC都相切,
∴DE=DF=r,
在Rt△ADE中,sinA==,
∴DA=r,
在Rt△CDF中,sinC==,
∴DA=r,
∵DA+DC=AC,
∴r+r=6,
解得r=,
即⊙D的半径为.
23.解:(1).
证明:延长DO交⊙O于E,
∵AC∥OD
∴
∵∠1=∠2
∴
∴;
(2)仍成立.
证明:延长DO交⊙O于点E,连接AD,
∵,
∴
∴∠3=∠D
∴AC∥OD.
24.证明:∵O为的中点,
∴OA=OB,
∴点O为所在圆的圆心,
连接AC、BD,则有AC=CD=BD,
∵∠AOC=∠COD,OA=OC=OD,
∴△ACO≌△DCO.
∴∠ACO=∠OCD.
∵∠OEF=∠OAE+∠AOE=45°+30°=75°,∠OCD==75°,
∴∠OEF=∠OCD,
∴CD∥AB,
∴∠AEC=∠OCD,
∴∠ACO=∠AEC.
故AC=AE,
同理,BF=BD.
又∵AC=CD=BD
∴AE=CD=BF.
25.证明:∵OC=OP,
∴∠1=∠2.
∵CP平分∠OCD,
∴∠2=∠3,
∴∠3=∠1,
∴CD∥OP,
∵CD⊥AB,
∴OP⊥AB.
∴=,
∴PA=PB.
26.解:由图可知,将△OAC顺时针旋转90°后可与△ODB重合,
∴S△OAC=S△OBD;
因此S阴影=S扇形OAB+S△OBD﹣S△OAC﹣S扇形OCD=S扇形OAB﹣S扇形OCD=π×(9﹣1)=2πcm2.
即阴影部分的面积是2πcm2.
27.解:∵正六边形的半径等于边长,
∴正六边形的边长a=2cm;
正六边形的周长l=6a=12cm;
正六边形的面积S=6××2×=.
故答案为:2cm,12cm,6cm2.
一.选择题
1.把圆的半径缩小到原来的,那么圆的面积缩小到原来的( )
A. B. C. D.
2.如图,D是的中点,则图中与∠ABD相等的角的个数是( )
A.4个 B.3个 C.2个 D.1个
3.如图,点C在线段AB上,以AB、AC为直径的半圆相切于点A,大圆的弦AE交小圆于点D,∠EAB=α,如DE=2,那么BC等于( )
A.2cosα B.2sinα C. D.
4.在圆柱形油槽内装有一些油,截面如图,油面宽AB为6dm,如果再注入一些油后,油面AB上升1dm,油面宽为8dm,圆柱形油槽直径MN为( )
A.6dm B.8dm C.10dm D.12dm
5.已知⊙O的半径为1,点P到O的距离为R,且方程x2﹣2x+R=0有实数根,则P( )
A.在⊙O的内部 B.在⊙O上
C.在⊙O外部 D.在⊙O的内部或圆上
6.已知在△ABC中,∠A:∠B:∠C=1:2:3,以B为圆心,BC为半径的⊙B与AC边的位置关系是( )
A.相离 B.相切 C.相交 D.不确定
7.在下列各结论中,正确的为( )
A.圆心角相等的两个扇形相同
B.圆心角相等的两个扇形的面积相等
C.两个面积相等的扇形的圆心角相等
D.同圆或等圆中面积相等的两个扇形的圆心角相等
8.在平行四边形、矩形、正方形、菱形、等腰梯形、直角梯形中,必定存在外接圆的有( )
A.1个 B.2个 C.3个 D.4个
9.下列命题中,真命题的个数为( )
①任意三点确定一个圆;②平分弦的直径垂直于弦;③90°的圆周角所对的弦是直径;④同弧或等弧所对的圆周角相等.
A.1个 B.2个 C.3个 D.4个
10.如图,PA=PB,OE⊥PA,OF⊥PB,则以下结论:①OP是∠APB的平分线;②PE=PF③CA=BD;④CD∥AB;其中正确的有( )个.
A.4 B.3 C.2 D.1
二.填空题
11.各边相等的圆内接多边形 正多边形;各角相等的圆内接多边形 正多边形.(填“是”或“不是”)
12.⊙O半径为3,圆心O到直线L的距离为d,若直线L与⊙O相交,则d的取值范围是 .
13.如图,⊙O是△ABC的外接圆,∠A=45°,BC=3,则⊙O的直径为 .
14.如果⊙O的半径为r,点P到圆心O的距离为d,那么:①点P在⊙O外,则 ;② ,则d=r;③ ,则d<r.
15.如图,△ABC内接于⊙O,D是劣弧弧AB上的一点,E是BC延长线上一点,AE交⊙O于F,为使△ADB∽△ACE,应补充的一个条件是 或 .
16.扇形的圆心角度数60°,面积6π,则扇形的弧长为 .
17.一个三角形的外心与内心恰好重合,这个三角形是 .
18.如图,EB、EC是⊙O的两条切线,B、C为切点,A是⊙O上的任意一点,若∠A=70°,则∠E= .
19.如图,水平放着的圆柱形排水管的截面为1000mm,其中水面宽AB=800mm,则水的最大深度为 mm.
20.如图1,平行四边形ABCD中,AB⊥AC,AB=6,AD=10,点P在边AD上运动,以P为圆心,PA为半径的⊙P与对角线AC交于A,E两点.不难发现,随着AP的变化,⊙P与平行四边形ABCD的边的公共点的个数也在变化.如图2,当⊙P与边CD相切时,⊙P与平行四边形ABCD的边有三个公共点.若公共点的个数为4,则相对应的AP的取值范围为 .
三.解答题
21.如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.
(1)求证:BD平分∠ABC;
(2)当BC=CE=2时,求DE的长度.
22.如图,在△ABC中,AB=5,AC=6,BC=7.
(1)求sinA和sinC的值;
(2)若⊙D的圆心D在边AC上,且⊙D与边AB、BC都相切,求⊙D的半径.
23.如图,AB是⊙O的直径.
(1)若OD∥AC,与的大小有什么关系?为什么?
(2)把(1)中的条件和结论交换一下,还能成立吗?说明理由.
24.如图所示,∠AOB=90°,O为所在圆的圆心,且C、D是的三等分点,AB分别交OC,OD于点E,F.求证:AE=BF=CD.
25.如图,已知AB和CD是⊙O的两条弦,且AB⊥CD,连接OC,作∠OCD的平分线交⊙O于P,连接PA、PB,
求证:PA=PB.
26.圆心角都是90°的扇形OAB与扇形OCD按如图所示的方式叠放在一起,连结AC,BD.若AO=3cm,OC=1cm,求阴影部分的面积.
27.已知正六边形ABCDEF的半径为2cm,求这个正六边形的边长、周长和面积.
参考答案与试题解析
一.选择题
1.解:设原来的圆的半径为r,则面积s1=πr2,
∴缩小到原来的后,s2=π(r)2=πr2,
∴==.
故选:D.
2.解:∵D是的中点,
∴弧AD=弧CD,
∴∠ABD=∠CBD=∠ACD=∠DAC.
故选:B.
3.解:连接CD、BE,过C点作CF∥AE交BE于点F,
点C在线段AB上,AB、AC为直径,
所以有DC⊥AE,BE⊥AE,
即得CD∥BE,且四边形DCFE为正方形,
即FC=DE=2,∠FCB=∠EAB=α,
在Rt△BCF中,BC=
故选:C.
4.解:根据题意画出图形,如图所示,EF=1dm,AB=6dm,CD=8dm,设圆的半径为r,
∵OE⊥CD,OF⊥AB,
∴CE=DE=4dm,AF=BF=3dm,
在Rt△OCE和△OAF中,
根据勾股定理得:OE==,OF==,
∴OE﹣OF=1,即﹣=1,
=+1,
两边平方得,r2﹣9=r2﹣16+2+1,
=3,
两边平方得,r2﹣16=9,
r2=25,
解得:r=5,
则圆柱形油槽直径MN为10dm.
故选:C.
5.解:因为方程有实数根,所以△=4﹣4R≥0,得到R≤1,
而圆的半径为1,说明点P到圆心的距离小于或等于半径,所以点P在圆内或圆上.
故选:D.
6.解:∵在△ABC中,∠A:∠B:∠C=1:2:3,
∴∠A=30°,∠B=60°,∠C=90°,
∴以B为圆心,BC为半径的⊙B与AC边的位置关系是相切.
故选:B.
7.解:因为不是在同一个圆中的扇形面积和圆心角都无法比较,
故可以排除A,B,C 而对于同一个圆中,
扇形的面积为:s=lα2,
其中l为圆的半径,α为圆心角
故选:D.
8.解:根据圆内接多边形的性质可得:矩形,正方形与等腰梯形必定存在外接圆.故选C.
9.解:①假命题,当三点在同一条直线上时,就不能确定一个圆了;
②假命题,当弦为直径时就不一定垂直了;
③真命题;
④真命题,同弧或等弧所对的圆周角相等.
故选:B.
10.解:
连接OP、OC、OA、OD、OB、CD、AB.
∵PC?PA=PD?PB(相交弦定理),PA=PB(已知),
∴PC=PD,
∴AC=BD;
在△AOC和△BOD中,
∵∠AOC=∠BOD(等弦对等角),
OA=OB(半径),
OD=OC(半径),
∴△AOC≌△BOD,
∴③CA=BD;
OE=OF;
又∵OE⊥PA,OF⊥PB,
∴①OP是∠APB的平分线;
∴②PE=PF;
在△PCD和△PAB中,
PC:PA=PD:PB,
∠DPC=∠BPA,
∴△PCD∽△PAB,
∴∠PDC=PBA,
∴④CD∥AB;
综上所述,①②③④均正确,故答案选A.
二.填空题
11.解:∵正多边形的各边相等,
∴各边所对的圆周角必然相等,
∴各边相等的圆内接多边形是正多边形;
∵圆内接多边形的各角相等;
举出一个反例:当四个角都是直角时,这个四边形可能是矩形,
∴各角相等的圆内接多边形不一定是正多边形.
故答案为:是,不是.
12.解:∵直线和圆相交,
∴d<r.
又∵d是直线到圆心的距离,⊙O半径为3,
∴d是非负数,
∴0≤d<3.
13.解:连接OB、OC,如图,
∵∠BOC=2∠A=90°,
而OB=OC,
∴△OBC为等腰直角三角形,
∴OB=BC=,
∴⊙O的直径为3.
故答案为3.
14.解:①∵点P在⊙O外,∴d>r;故填:d>r.
②∵d=r,∴点在圆上;故填:点P在⊙O上.
③∵d<r,∴点在圆内;故填:点P在⊙O内.
15.解:∵四边形ADBC是⊙O的内接四边形,
∴∠ACE=∠D,∴当∠BAD=∠EAC或∠ABD=∠E时,△ADB∽△ACE.
16.解:6π=,
解得r=6,
弧长==2π.
17.解:根据等边三角形的性质可知,一个三角形的外心与内心恰好重合,这个三角形是等边三角形.
18.解:连接OB,OC.
则∠BOC=2∠A=2×70=140°,
∵EB、EC是⊙O的两条切线,
∴∠EBO=∠ECO=90°,
∴∠E=360°﹣∠BOC﹣∠EBO﹣∠ECO=360°﹣140°﹣90°﹣90°=40°.
故答案是:40°.
19.解:过O点作OC⊥AB,C为垂足,交⊙O于D,连OA,如图,
OA=500mm,AB=800mm,
∵OC⊥AB,
∴AC=BC=400mm,
在Rt△AOC中,OA2=AC2+OC2,
∴OC==300,
∴CD=300+500=800(mm),
即水的最大深度为800mm.
故答案为800mm.
20.解:∵平行四边形ABCD中,AB=6,AD=10,
∴BC=AD=10,
∵AB⊥AC,
∴在Rt△ABC中,由勾股定理得:AC===8,
如图2所示,连接PF,
设AP=x,则DP=10﹣x,PF=x,
∵⊙P与边CD相切于点F,
∴PF⊥CD,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AB⊥AC,
∴AC⊥CD,
∴AC∥PF,
∴△DPF∽△DAC,
∴=,
∴=,
∴x=,
即AP=;
当⊙P与BC相切时,设切点为G,如图3,
S?ABCD=×6×8×2=10PG,
∴PG=,
①当⊙P与边AD、CD分别有两个公共点时,<AP<,即此时⊙P与平行四边形ABCD的边的公共点的个数为4;
②⊙P过点A、C、D三点,如图4,⊙P与平行四边形ABCD的边的公共点的个数为4,此时AP=5,
综上所述,AP的值的取值范围是:<AP<或AP=5,
故答案为:<AP<或AP=5.
三.解答题
21.(1)证明:∵OD⊥AC,
∴=,
∴∠ABD=∠CBD,
∴BD平分∠ABC;
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵OD⊥AC,
∴AE=CE=2,
在Rt△ABC中,AB==2,
∴OD=,
∵AE=CE,OA=OB,
∴OE为△ABC的中位线,
∴OE=BC=1,
∴DE=﹣1.
22.解:(1)作BH⊥AC于H,如图,
设AH=x,则CH=6﹣x,
在Rt△ABH中,BH2+x2=52,
在Rt△CBH中,BH2+(6﹣x)2=72,
解得x=1,BH=2,
在Rt△ABH中,sinA==;
在Rt△CBH中,sinC==;
即sinA=,sinC=;
(2)作DE⊥AB于E,DF⊥BC于F,如图,设⊙D的半径为r,
∵⊙D与边AB、BC都相切,
∴DE=DF=r,
在Rt△ADE中,sinA==,
∴DA=r,
在Rt△CDF中,sinC==,
∴DA=r,
∵DA+DC=AC,
∴r+r=6,
解得r=,
即⊙D的半径为.
23.解:(1).
证明:延长DO交⊙O于E,
∵AC∥OD
∴
∵∠1=∠2
∴
∴;
(2)仍成立.
证明:延长DO交⊙O于点E,连接AD,
∵,
∴
∴∠3=∠D
∴AC∥OD.
24.证明:∵O为的中点,
∴OA=OB,
∴点O为所在圆的圆心,
连接AC、BD,则有AC=CD=BD,
∵∠AOC=∠COD,OA=OC=OD,
∴△ACO≌△DCO.
∴∠ACO=∠OCD.
∵∠OEF=∠OAE+∠AOE=45°+30°=75°,∠OCD==75°,
∴∠OEF=∠OCD,
∴CD∥AB,
∴∠AEC=∠OCD,
∴∠ACO=∠AEC.
故AC=AE,
同理,BF=BD.
又∵AC=CD=BD
∴AE=CD=BF.
25.证明:∵OC=OP,
∴∠1=∠2.
∵CP平分∠OCD,
∴∠2=∠3,
∴∠3=∠1,
∴CD∥OP,
∵CD⊥AB,
∴OP⊥AB.
∴=,
∴PA=PB.
26.解:由图可知,将△OAC顺时针旋转90°后可与△ODB重合,
∴S△OAC=S△OBD;
因此S阴影=S扇形OAB+S△OBD﹣S△OAC﹣S扇形OCD=S扇形OAB﹣S扇形OCD=π×(9﹣1)=2πcm2.
即阴影部分的面积是2πcm2.
27.解:∵正六边形的半径等于边长,
∴正六边形的边长a=2cm;
正六边形的周长l=6a=12cm;
正六边形的面积S=6××2×=.
故答案为:2cm,12cm,6cm2.
