2020-2021学年湘教新版九年级下册数学《第1章 二次函数》单元测试卷(word版含解析)
文档属性
| 名称 | 2020-2021学年湘教新版九年级下册数学《第1章 二次函数》单元测试卷(word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 177.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-28 00:00:00 | ||
图片预览




文档简介
2020-2021学年湘教新版九年级下册数学《第1章 二次函数》单元测试卷
一.选择题
1.下列各式中,y是关于x的二次函数的是( )
A.x2y+x=1 B.x2﹣xy=5 C.y2=x2+2 D.x2+y+2=0
2.形状与抛物线y=﹣x2﹣2相同,对称轴是x=﹣2,且过点(0,3)的抛物线是( )
A.y=x2+4x+3
B.y=﹣x2﹣4x+3
C.y=﹣x2+4x+3
D.y=x2+4x+3或y=﹣x2﹣4x+3
3.根据抛物线y=x2+3x﹣1与x轴的交点的坐标,可以求出下列方程中哪个方程的近似解( )
A.x2﹣1=﹣3x B.x2+3x+1=0 C.3x2+x﹣1=0 D.x2﹣3x+1=0
4.如果二次函数y=ax2+m的值恒大于0,那么必有( )
A.a>0,m取任意实数 B.a>0,m>0
C.a<0,m>0 D.a,m均可取任意实数
5.对于抛物线y=x2和y=﹣x2在同一坐标系里的位置,下列说法错误的是( )
A.两条抛物线关于x轴对称
B.两条抛物线关于原点对称
C.两条抛物线关于y轴对称
D.两条抛物线的交点为原点
6.某超市将进货单价为l8元的商品按每件20元销售时,每日可销售100件,如果每件提价1元,日销售就要减少10件,那么把商品的售出价定为多少元时,才能使每天获得的利润最大?( )
A.22元 B.24元 C.26元 D.28元
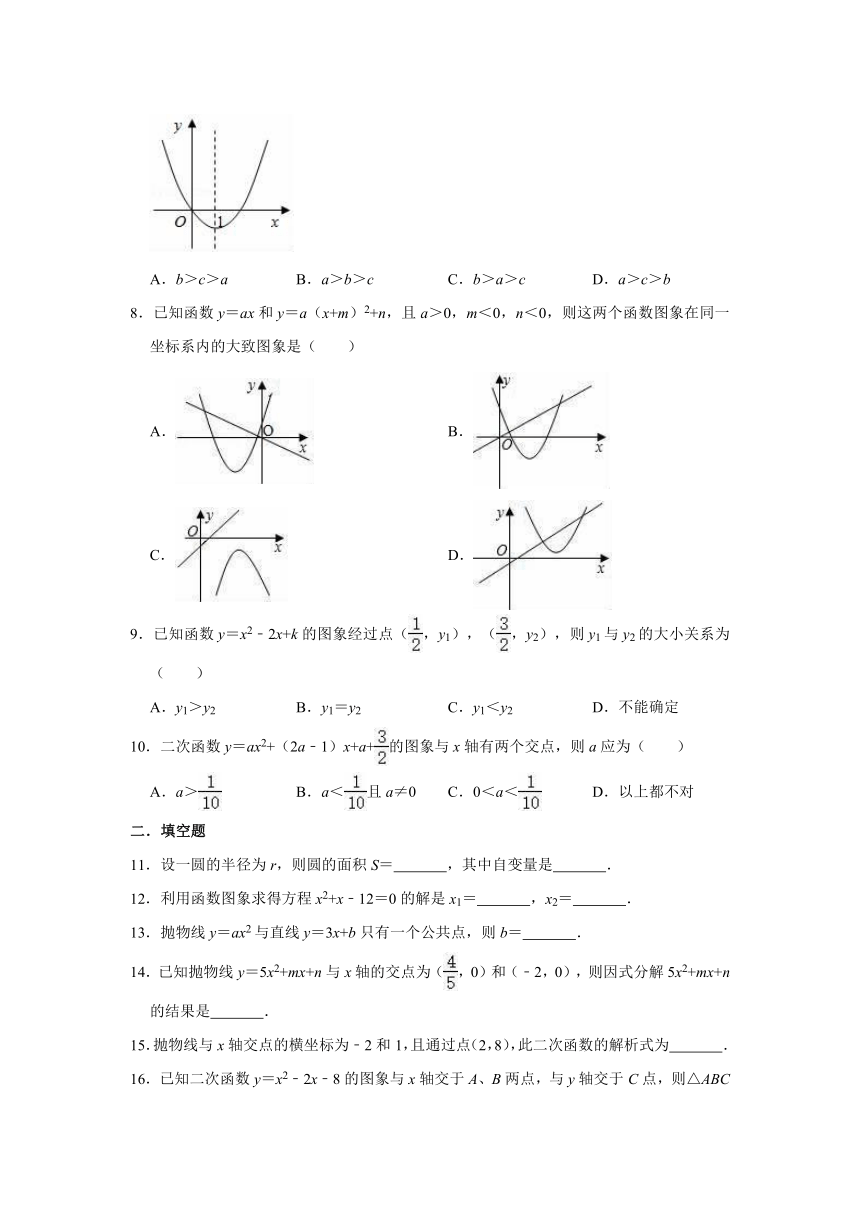
7.若二次函数y=ax2+bx+c(a≠0)的图象如图所示.则实数a,b,c的大小关系是( )
A.b>c>a B.a>b>c C.b>a>c D.a>c>b
8.已知函数y=ax和y=a(x+m)2+n,且a>0,m<0,n<0,则这两个函数图象在同一坐标系内的大致图象是( )
A. B.
C. D.
9.已知函数y=x2﹣2x+k的图象经过点(,y1),(,y2),则y1与y2的大小关系为( )
A.y1>y2 B.y1=y2 C.y1<y2 D.不能确定
10.二次函数y=ax2+(2a﹣1)x+a+的图象与x轴有两个交点,则a应为( )
A.a> B.a<且a≠0 C.0<a< D.以上都不对
二.填空题
11.设一圆的半径为r,则圆的面积S= ,其中自变量是 .
12.利用函数图象求得方程x2+x﹣12=0的解是x1= ,x2= .
13.抛物线y=ax2与直线y=3x+b只有一个公共点,则b= .
14.已知抛物线y=5x2+mx+n与x轴的交点为(,0)和(﹣2,0),则因式分解5x2+mx+n的结果是 .
15.抛物线与x轴交点的横坐标为﹣2和1,且通过点(2,8),此二次函数的解析式为 .
16.已知二次函数y=x2﹣2x﹣8的图象与x轴交于A、B两点,与y轴交于C点,则△ABC的面积为 .
17.已知二次函数y=x2﹣2x﹣3的函数值y<0,则x的取值范围为 .
18.已知点(1,y1),(2,y2),(4,y3)在函数y=x2﹣4x+3的图象上,那么y1,y2,y3的大小关系是 .
19.若函数y=(m2﹣1)x3+(m+1)x2的图象是抛物线,则m= .
20.如图,一小孩将一只皮球从A处抛出去,它所经过的路线是某个二次函数图象的一部分,如果他的出手处A距地面的距离OA为1 m,球路的最高点B(8,9),则小孩将球抛出了约 米(精确到0.1 m).
三.解答题
21.已知抛物线经过三个点A(2,6),B(﹣1,0),C(3,0),那么二次函数的解析式是?它的顶点坐标是?
22.已知抛物线y=2x2﹣3x+m(m为常数)与x轴交于A,B两点,且线段AB的长为.
(1)求m的值;
(2)若该抛物线的顶点为P,求△ABP的面积.
23.已知是x的二次函数,求出它的解析式.
24.对于抛物线y=x2+bx+c,给出以下陈述:
①它的对称轴为x=2;
②它与x轴有两个交点为A、B;
③△APB的面积不小于27(P为抛物线的顶点).
求①、②、③得以同时成立时,常数b、c的取值范围.
25.已知二次函数y=﹣2x2,怎样平移这个函数的图象,才能使它经过(0,1)和(1,3)两点?写出平移后的函数解析式.
26.某果园有100棵橙子树,每一棵树均结600个橙子.现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子.
(1)假设果园增种x棵橙子树,那么果园共有多少棵橙子树?这时平均每棵树结多少个橙子?
(2)如果果园橙子的总产量为y个,那么请你写出y与x之间的关系式.
27.已知二次函数y=﹣x2+bx+c的图象经过点A(﹣3,﹣6),并与x轴交于点B(﹣1,0)和点C,顶点为P.
(1)求二次函数的解析式;
(2)设点M为线段OC上一点,且∠MPC=∠BAC,求点M的坐标;
说明:若(2)你经历反复探索没有获得解题思路,请你在不改变点M的位置的情况下添加一个条件解答此题,此时(2)最高得分为3分.
参考答案与试题解析
一.选择题
1.解:A、整理后,不符合二次函数的一般形式,错误;
B、整理后,不符合二次函数的一般形式,错误;
C、这里,y的指数是2,不是函数,错误;
D、整理为y=﹣x2﹣2,是二次函数,正确.
故选:D.
2.解:设所求抛物线的函数关系式为y=ax2+bx+c,由抛物线过点(0,3),可得:c=3,
由抛物线形状与y=﹣x2﹣2相同,
分为两种情况:①开口向下,则a<0,
又∵对称轴x=﹣2,则x=﹣=﹣2.则b<0,
由此可得出B选项符合题意.
②开口向下,则a>0,
又∵对称轴x=﹣2,则x=﹣=﹣2.则b>0,
由此可得出A选项符合题意,
综合上述,符合条件的是选项D,
故选:D.
3.解:∵抛物线y=x2+3x﹣1与x轴的交点的横坐标就是方程x2+3x﹣1=0的根,
∴可以求出方程x2+3x﹣1=0的根,
方程x2﹣1=﹣3x与方程x2+3x﹣1=0等价,
∴可以求出方程x2﹣1=﹣3x的根.
故选:A.
4.解:由题意得:二次函数y=ax2+m的最小值大于0,
∴a>0,m>0,
故选:B.
5.解:两个函数的顶点坐标都是(0,0),二次项的系数互为相反数,说明一个开口向上,一个开口向下.
故两条抛物线的交点为原点,两条抛物线关于x轴对称且两条抛物线关于原点对称.
故选:C.
6.解:设利润为y,售价定为每件x元,
由题意得,y=(x﹣18)×[100﹣10(x﹣20)],
整理得:y=﹣10x2+480x﹣5400=﹣10(x﹣24)2+360,
∵﹣10<0,
∴开口向下,
故当x=24时,y有最大值.
故选:B.
7.解:∵图象开口向上,经过原点,对称轴在y轴右侧,
∴a>0,c=0,﹣=1,
∴b=﹣2a<0,
∴a>c>b,
故选:D.
8.解:由解析式y=a(x+m)2+n可知,a>0,图象开口向上,其顶点坐标为(﹣m,n),又因为m<0,n<0;所以顶点坐标在第四象限,排除A、D;
C中,由二次函数图象可知a<0,而由一次函数的图象可知a>0,两者相矛盾,排除C;选项B正确.
故选:B.
9.解:∵对称轴为x=﹣=1,
∴点(,y1)的对称点的横坐标为,即称点坐标为(,y2),
∴y1=y2.
故选:B.
10.解:∵二次函数y=ax2+(2a﹣1)x+a+的图象与x轴有两个交点,
∴b2﹣4ac=(2a﹣1)2﹣4×a×(a+)=4a2+1﹣4a﹣4a2﹣6a=1﹣10a>0,
∴a<且a≠0,
故选:B.
二.填空题
11.解:由圆的面积公式得:
S=πr2,自变量是r.
12.解:∵方程x2+x﹣12=0的解就是函数y=x2+x﹣12的图象与x轴的交点的横坐标,
而y=x2+x﹣12的图象如图所示:
∴y=x2+x﹣12的图象与x轴的交点坐标为(﹣4,0)、(3,0),
∴方程x2+x﹣12=0的解是x1=﹣4,x2=3.
13.解:∵抛物线y=ax2与直线y=3x+b只有一个公共点,
∴ax2=3x+b只有一个解,
即ax2﹣3x﹣b=0只有一个解,
∴△=9+4ab=0.
解得b=﹣.
14.解:∵抛物线y=5x2+mx+n与x轴的交点为(,0)和(﹣2,0),a=5,
∴抛物线的解析式用交点式表示为y=5(x+2)(x﹣)
即:5x2+mx+n=5(x+2)(x﹣).
15.解:根据题意设y=a(x+2)(x﹣1)(a≠0),
将(2,8)代入得:a(2+2)(2﹣1)=8,即4a=8,
解得:a=2,
则二次函数解析式为y=2(x+2)(x﹣1)=2x2+2x﹣4.
故答案为:y=2x2+2x﹣4
16.解:根据二次函数y=x2﹣2x﹣8,可得A、B两点的横坐标为﹣2,4;
C的纵坐标为﹣8;
则△ABC的面积为×8×6=24.
17.解:当y=0时,即x2﹣2x﹣3=0,
∴x1=﹣1,x2=3,
∴图象与x轴的交点是(﹣1,0),(3,0),
当y<0时,图象在x轴的下方,
此时﹣1<x<3.
故填空答案:﹣1<x<3.
18.解:因为函数y=x2﹣4x+3对称轴是x=2,且开口向上,
所以,距离对称轴越近,函数值越小;反之也成立.
比较可得:(2,y2)最近,而(4,y3)最远;
故有y2<y1<y3.
19.解:根据题意,由m+1≠0,得m≠﹣1
且m2﹣1=0,得m=±1
所以m=1.
20.解:根据题意,设二次函数顶点式:y=a(x﹣8)2+9
把A(0,1)代入得a=﹣,
∴y=﹣(x﹣8)2+9,
当y=0时,解得x1=8+6≈16.5,x2=8﹣6<0(舍去).
∴小孩将球抛出了约16.5米.
三.解答题
21.解:设二次函数解析式为y=ax2+bx+c,
根据题意得,
解得.
所以二次函数的解析式为y=﹣2x2+4x+6,
∵y=﹣2x2+4x+6=﹣2(x﹣1)2+8,
∴抛物线的顶点坐标为(1,8).
22.解:(1)设抛物线与x轴交点的横坐标为x1,x2,
∴关于x的方程2x2﹣3x+m=0,
∴△=(﹣3)2﹣8m=9﹣8m>0,
解得m<,
∵x1+x2=,x1?x2=,
∴AB=|x1﹣x2|==,
又∵AB=,
∴=,
∴m=1;
(2)∵m=1,
∴y=2x2﹣3x+1,
∴==﹣,
∵AB=,
∴S△ABP=×=.
23.解:由二次函数的定义,可知m2+m≠0,即m≠0,m≠﹣1
又因为m2﹣2m﹣1=2,m2﹣2m﹣3=0
解得m=3或m=﹣1(不合题意,舍去)
所以m=3
故y=12x2+9.
24.解:∵抛物线y=x2+bx+c=(x+)2+,抛物线y=x2+bx+c的对称轴为x=2,
∴﹣=2,则b=﹣4,
∴P点的纵坐标是=c﹣4,
又∵它与x轴有两个交点为A、B,
∴△=b2﹣4ac=16﹣4c>0,且AB===2
解得 c<4,①
又△APB的面积不小于27,
∴×2×|c﹣4|≥27,即×|c﹣4|≥27②
由①②解得 c≤﹣5.
综上所述,b的值是﹣4,c的取值范围是c≤﹣5.
25.解:设y=﹣2x2+bx+c,把(0,1)(1,3)代入,
得c=1,﹣2+b+c=3,
解得b=4.
∴平移后的函数解析式为y=﹣2x2+4x+1=﹣2(x﹣1)2+3.
∵原抛物线的顶点为(0,0),
∴新抛物线的顶点为(1,3).
∴将原二次函数y=﹣2x2先向右平移1个单位,再向上平移3个单位,可得y=﹣2x2+4x+1的图象.
26.解:(1)假设果园增种x棵橙子树,那么果园共有(x+100)棵橙子树,
∵每多种一棵树,平均每棵树就会少结5个橙子,
∴这时平均每棵树就会少结5x个橙子,
则平均每棵树结(600﹣5x)个橙子.
答:假设果园增种x棵橙子树,那么果园共有(x+100)棵橙子树,这时平均每棵树结(600﹣5x)个橙子.
(2)如果果园橙子的总产量为y,
则y=(x+100)(600﹣5x)
=﹣5x2+100x+60000.
27.解:把两点代入求解得:
﹣3b+c=0,
b﹣c+=0,
解得:b=1,c=,
代入原函数解析式得:y=﹣x2+x+.
(2)如图所示:M点在OC上,
由题目可知∠MPC=∠BAC,点P的坐标为(1,2),
由已知个点坐标可以求得:CP=,AC=6,BC=4,∠PCM=∠ACB=45°;
由以上可以知道△PCM与△ACB相似,
所以有:,
解得:CM=,所以M点的坐标为(),
答:M点的坐标为().
一.选择题
1.下列各式中,y是关于x的二次函数的是( )
A.x2y+x=1 B.x2﹣xy=5 C.y2=x2+2 D.x2+y+2=0
2.形状与抛物线y=﹣x2﹣2相同,对称轴是x=﹣2,且过点(0,3)的抛物线是( )
A.y=x2+4x+3
B.y=﹣x2﹣4x+3
C.y=﹣x2+4x+3
D.y=x2+4x+3或y=﹣x2﹣4x+3
3.根据抛物线y=x2+3x﹣1与x轴的交点的坐标,可以求出下列方程中哪个方程的近似解( )
A.x2﹣1=﹣3x B.x2+3x+1=0 C.3x2+x﹣1=0 D.x2﹣3x+1=0
4.如果二次函数y=ax2+m的值恒大于0,那么必有( )
A.a>0,m取任意实数 B.a>0,m>0
C.a<0,m>0 D.a,m均可取任意实数
5.对于抛物线y=x2和y=﹣x2在同一坐标系里的位置,下列说法错误的是( )
A.两条抛物线关于x轴对称
B.两条抛物线关于原点对称
C.两条抛物线关于y轴对称
D.两条抛物线的交点为原点
6.某超市将进货单价为l8元的商品按每件20元销售时,每日可销售100件,如果每件提价1元,日销售就要减少10件,那么把商品的售出价定为多少元时,才能使每天获得的利润最大?( )
A.22元 B.24元 C.26元 D.28元
7.若二次函数y=ax2+bx+c(a≠0)的图象如图所示.则实数a,b,c的大小关系是( )
A.b>c>a B.a>b>c C.b>a>c D.a>c>b
8.已知函数y=ax和y=a(x+m)2+n,且a>0,m<0,n<0,则这两个函数图象在同一坐标系内的大致图象是( )
A. B.
C. D.
9.已知函数y=x2﹣2x+k的图象经过点(,y1),(,y2),则y1与y2的大小关系为( )
A.y1>y2 B.y1=y2 C.y1<y2 D.不能确定
10.二次函数y=ax2+(2a﹣1)x+a+的图象与x轴有两个交点,则a应为( )
A.a> B.a<且a≠0 C.0<a< D.以上都不对
二.填空题
11.设一圆的半径为r,则圆的面积S= ,其中自变量是 .
12.利用函数图象求得方程x2+x﹣12=0的解是x1= ,x2= .
13.抛物线y=ax2与直线y=3x+b只有一个公共点,则b= .
14.已知抛物线y=5x2+mx+n与x轴的交点为(,0)和(﹣2,0),则因式分解5x2+mx+n的结果是 .
15.抛物线与x轴交点的横坐标为﹣2和1,且通过点(2,8),此二次函数的解析式为 .
16.已知二次函数y=x2﹣2x﹣8的图象与x轴交于A、B两点,与y轴交于C点,则△ABC的面积为 .
17.已知二次函数y=x2﹣2x﹣3的函数值y<0,则x的取值范围为 .
18.已知点(1,y1),(2,y2),(4,y3)在函数y=x2﹣4x+3的图象上,那么y1,y2,y3的大小关系是 .
19.若函数y=(m2﹣1)x3+(m+1)x2的图象是抛物线,则m= .
20.如图,一小孩将一只皮球从A处抛出去,它所经过的路线是某个二次函数图象的一部分,如果他的出手处A距地面的距离OA为1 m,球路的最高点B(8,9),则小孩将球抛出了约 米(精确到0.1 m).
三.解答题
21.已知抛物线经过三个点A(2,6),B(﹣1,0),C(3,0),那么二次函数的解析式是?它的顶点坐标是?
22.已知抛物线y=2x2﹣3x+m(m为常数)与x轴交于A,B两点,且线段AB的长为.
(1)求m的值;
(2)若该抛物线的顶点为P,求△ABP的面积.
23.已知是x的二次函数,求出它的解析式.
24.对于抛物线y=x2+bx+c,给出以下陈述:
①它的对称轴为x=2;
②它与x轴有两个交点为A、B;
③△APB的面积不小于27(P为抛物线的顶点).
求①、②、③得以同时成立时,常数b、c的取值范围.
25.已知二次函数y=﹣2x2,怎样平移这个函数的图象,才能使它经过(0,1)和(1,3)两点?写出平移后的函数解析式.
26.某果园有100棵橙子树,每一棵树均结600个橙子.现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子.
(1)假设果园增种x棵橙子树,那么果园共有多少棵橙子树?这时平均每棵树结多少个橙子?
(2)如果果园橙子的总产量为y个,那么请你写出y与x之间的关系式.
27.已知二次函数y=﹣x2+bx+c的图象经过点A(﹣3,﹣6),并与x轴交于点B(﹣1,0)和点C,顶点为P.
(1)求二次函数的解析式;
(2)设点M为线段OC上一点,且∠MPC=∠BAC,求点M的坐标;
说明:若(2)你经历反复探索没有获得解题思路,请你在不改变点M的位置的情况下添加一个条件解答此题,此时(2)最高得分为3分.
参考答案与试题解析
一.选择题
1.解:A、整理后,不符合二次函数的一般形式,错误;
B、整理后,不符合二次函数的一般形式,错误;
C、这里,y的指数是2,不是函数,错误;
D、整理为y=﹣x2﹣2,是二次函数,正确.
故选:D.
2.解:设所求抛物线的函数关系式为y=ax2+bx+c,由抛物线过点(0,3),可得:c=3,
由抛物线形状与y=﹣x2﹣2相同,
分为两种情况:①开口向下,则a<0,
又∵对称轴x=﹣2,则x=﹣=﹣2.则b<0,
由此可得出B选项符合题意.
②开口向下,则a>0,
又∵对称轴x=﹣2,则x=﹣=﹣2.则b>0,
由此可得出A选项符合题意,
综合上述,符合条件的是选项D,
故选:D.
3.解:∵抛物线y=x2+3x﹣1与x轴的交点的横坐标就是方程x2+3x﹣1=0的根,
∴可以求出方程x2+3x﹣1=0的根,
方程x2﹣1=﹣3x与方程x2+3x﹣1=0等价,
∴可以求出方程x2﹣1=﹣3x的根.
故选:A.
4.解:由题意得:二次函数y=ax2+m的最小值大于0,
∴a>0,m>0,
故选:B.
5.解:两个函数的顶点坐标都是(0,0),二次项的系数互为相反数,说明一个开口向上,一个开口向下.
故两条抛物线的交点为原点,两条抛物线关于x轴对称且两条抛物线关于原点对称.
故选:C.
6.解:设利润为y,售价定为每件x元,
由题意得,y=(x﹣18)×[100﹣10(x﹣20)],
整理得:y=﹣10x2+480x﹣5400=﹣10(x﹣24)2+360,
∵﹣10<0,
∴开口向下,
故当x=24时,y有最大值.
故选:B.
7.解:∵图象开口向上,经过原点,对称轴在y轴右侧,
∴a>0,c=0,﹣=1,
∴b=﹣2a<0,
∴a>c>b,
故选:D.
8.解:由解析式y=a(x+m)2+n可知,a>0,图象开口向上,其顶点坐标为(﹣m,n),又因为m<0,n<0;所以顶点坐标在第四象限,排除A、D;
C中,由二次函数图象可知a<0,而由一次函数的图象可知a>0,两者相矛盾,排除C;选项B正确.
故选:B.
9.解:∵对称轴为x=﹣=1,
∴点(,y1)的对称点的横坐标为,即称点坐标为(,y2),
∴y1=y2.
故选:B.
10.解:∵二次函数y=ax2+(2a﹣1)x+a+的图象与x轴有两个交点,
∴b2﹣4ac=(2a﹣1)2﹣4×a×(a+)=4a2+1﹣4a﹣4a2﹣6a=1﹣10a>0,
∴a<且a≠0,
故选:B.
二.填空题
11.解:由圆的面积公式得:
S=πr2,自变量是r.
12.解:∵方程x2+x﹣12=0的解就是函数y=x2+x﹣12的图象与x轴的交点的横坐标,
而y=x2+x﹣12的图象如图所示:
∴y=x2+x﹣12的图象与x轴的交点坐标为(﹣4,0)、(3,0),
∴方程x2+x﹣12=0的解是x1=﹣4,x2=3.
13.解:∵抛物线y=ax2与直线y=3x+b只有一个公共点,
∴ax2=3x+b只有一个解,
即ax2﹣3x﹣b=0只有一个解,
∴△=9+4ab=0.
解得b=﹣.
14.解:∵抛物线y=5x2+mx+n与x轴的交点为(,0)和(﹣2,0),a=5,
∴抛物线的解析式用交点式表示为y=5(x+2)(x﹣)
即:5x2+mx+n=5(x+2)(x﹣).
15.解:根据题意设y=a(x+2)(x﹣1)(a≠0),
将(2,8)代入得:a(2+2)(2﹣1)=8,即4a=8,
解得:a=2,
则二次函数解析式为y=2(x+2)(x﹣1)=2x2+2x﹣4.
故答案为:y=2x2+2x﹣4
16.解:根据二次函数y=x2﹣2x﹣8,可得A、B两点的横坐标为﹣2,4;
C的纵坐标为﹣8;
则△ABC的面积为×8×6=24.
17.解:当y=0时,即x2﹣2x﹣3=0,
∴x1=﹣1,x2=3,
∴图象与x轴的交点是(﹣1,0),(3,0),
当y<0时,图象在x轴的下方,
此时﹣1<x<3.
故填空答案:﹣1<x<3.
18.解:因为函数y=x2﹣4x+3对称轴是x=2,且开口向上,
所以,距离对称轴越近,函数值越小;反之也成立.
比较可得:(2,y2)最近,而(4,y3)最远;
故有y2<y1<y3.
19.解:根据题意,由m+1≠0,得m≠﹣1
且m2﹣1=0,得m=±1
所以m=1.
20.解:根据题意,设二次函数顶点式:y=a(x﹣8)2+9
把A(0,1)代入得a=﹣,
∴y=﹣(x﹣8)2+9,
当y=0时,解得x1=8+6≈16.5,x2=8﹣6<0(舍去).
∴小孩将球抛出了约16.5米.
三.解答题
21.解:设二次函数解析式为y=ax2+bx+c,
根据题意得,
解得.
所以二次函数的解析式为y=﹣2x2+4x+6,
∵y=﹣2x2+4x+6=﹣2(x﹣1)2+8,
∴抛物线的顶点坐标为(1,8).
22.解:(1)设抛物线与x轴交点的横坐标为x1,x2,
∴关于x的方程2x2﹣3x+m=0,
∴△=(﹣3)2﹣8m=9﹣8m>0,
解得m<,
∵x1+x2=,x1?x2=,
∴AB=|x1﹣x2|==,
又∵AB=,
∴=,
∴m=1;
(2)∵m=1,
∴y=2x2﹣3x+1,
∴==﹣,
∵AB=,
∴S△ABP=×=.
23.解:由二次函数的定义,可知m2+m≠0,即m≠0,m≠﹣1
又因为m2﹣2m﹣1=2,m2﹣2m﹣3=0
解得m=3或m=﹣1(不合题意,舍去)
所以m=3
故y=12x2+9.
24.解:∵抛物线y=x2+bx+c=(x+)2+,抛物线y=x2+bx+c的对称轴为x=2,
∴﹣=2,则b=﹣4,
∴P点的纵坐标是=c﹣4,
又∵它与x轴有两个交点为A、B,
∴△=b2﹣4ac=16﹣4c>0,且AB===2
解得 c<4,①
又△APB的面积不小于27,
∴×2×|c﹣4|≥27,即×|c﹣4|≥27②
由①②解得 c≤﹣5.
综上所述,b的值是﹣4,c的取值范围是c≤﹣5.
25.解:设y=﹣2x2+bx+c,把(0,1)(1,3)代入,
得c=1,﹣2+b+c=3,
解得b=4.
∴平移后的函数解析式为y=﹣2x2+4x+1=﹣2(x﹣1)2+3.
∵原抛物线的顶点为(0,0),
∴新抛物线的顶点为(1,3).
∴将原二次函数y=﹣2x2先向右平移1个单位,再向上平移3个单位,可得y=﹣2x2+4x+1的图象.
26.解:(1)假设果园增种x棵橙子树,那么果园共有(x+100)棵橙子树,
∵每多种一棵树,平均每棵树就会少结5个橙子,
∴这时平均每棵树就会少结5x个橙子,
则平均每棵树结(600﹣5x)个橙子.
答:假设果园增种x棵橙子树,那么果园共有(x+100)棵橙子树,这时平均每棵树结(600﹣5x)个橙子.
(2)如果果园橙子的总产量为y,
则y=(x+100)(600﹣5x)
=﹣5x2+100x+60000.
27.解:把两点代入求解得:
﹣3b+c=0,
b﹣c+=0,
解得:b=1,c=,
代入原函数解析式得:y=﹣x2+x+.
(2)如图所示:M点在OC上,
由题目可知∠MPC=∠BAC,点P的坐标为(1,2),
由已知个点坐标可以求得:CP=,AC=6,BC=4,∠PCM=∠ACB=45°;
由以上可以知道△PCM与△ACB相似,
所以有:,
解得:CM=,所以M点的坐标为(),
答:M点的坐标为().
