旋转对称图形导学案
图片预览
文档简介
旋转对称图形导学案 备课人 李建朋
班级 姓名 2011年11月20日
学习目标:1.进一步巩固图形的平移、旋转等概念,并能运用相关知识解决问题;
2.理解旋转对称图形的概念,能够熟练判断图形是否旋转对称图形,能够说出旋转对称图形形成的过程.
学习重点:旋转对称图形的概念.
学习难点:综合运用变换知识解决有关问题.
学习过程:
一、课前练习
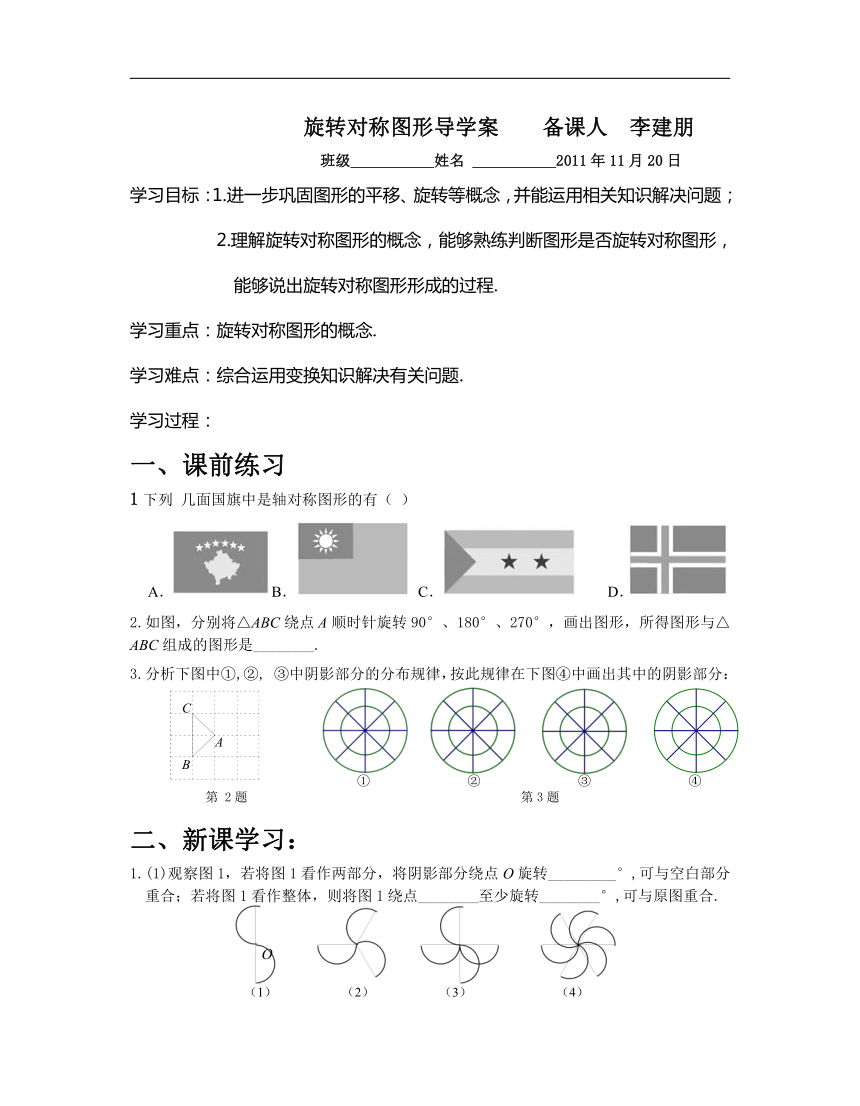
1下列 几面国旗中是轴对称图形的有( )
A.B. C. D.
2.如图,分别将△ABC绕点A顺时针旋转90°、180°、270°,画出图形,所得图形与△ABC组成的图形是________.
3.分析下图中①,②, ③中阴影部分的分布规律,按此规律在下图④中画出其中的阴影部分:
二、新课学习:
1.(1)观察图1,若将图1看作两部分,将阴影部分绕点O旋转_________°,可与空白部分重合;若将图1看作整体,则将图1绕点________至少旋转________°,可与原图重合.
(2)若将图2看作整体,则将图2绕点________至少旋转________°,可与原图重合.
(3)若将图3看作整体,则将图3绕点________至少旋转________°,可与原图重合.
(4)若将图4看作整体,则将图4绕点________至少旋转________°,可与原图重合.
结论:旋转对称图形的特征_______________________________________________.
以上图形中,_________________________是旋转对称图形.
比较:轴对称图形与旋转对称图形有何异同?
(1)相同点:
(2)不同点:
三应用迁移:
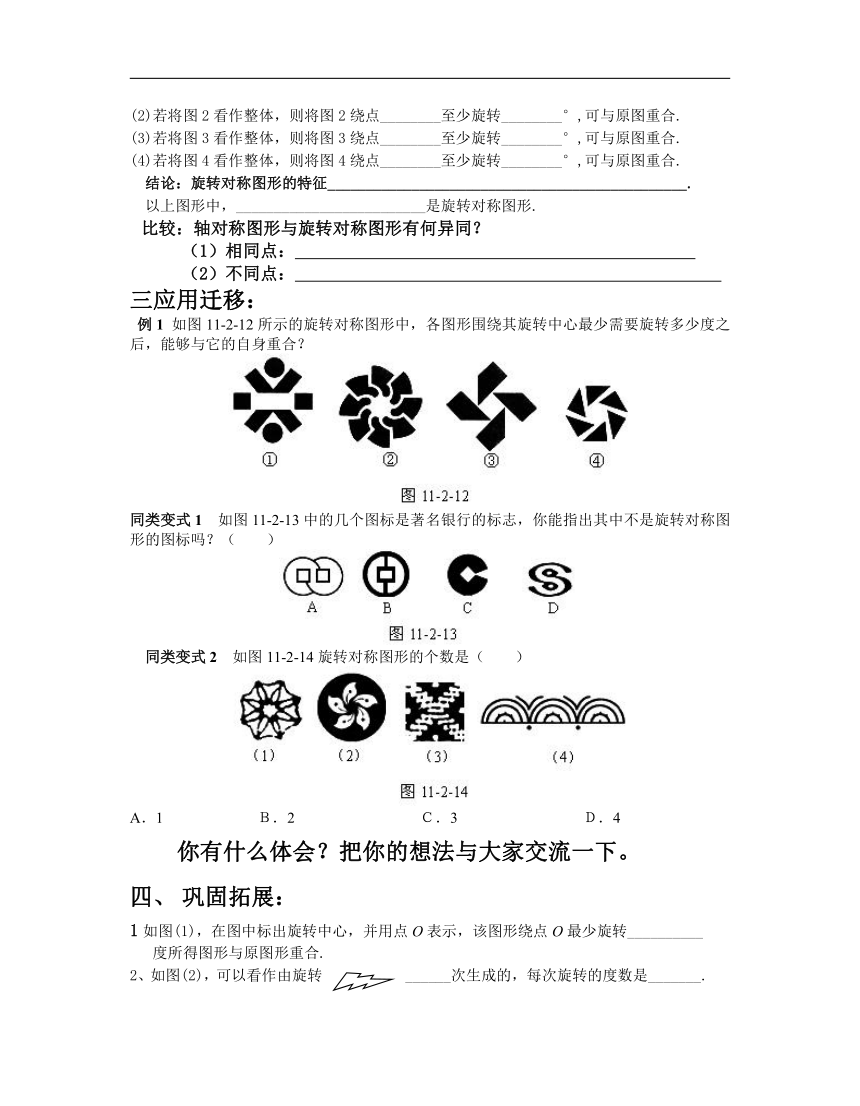
例1 如图11-2-12所示的旋转对称图形中,各图形围绕其旋转中心最少需要旋转多少度之后,能够与它的自身重合?
同类变式1 如图11-2-13中的几个图标是著名银行的标志,你能指出其中不是旋转对称图形的图标吗?( )
同类变式2 如图11-2-14旋转对称图形的个数是( )
A.1 B.2 C.3 D.4
你有什么体会?把你的想法与大家交流一下。
巩固拓展:
1如图(1),在图中标出旋转中心,并用点O表示,该图形绕点O最少旋转__________
度所得图形与原图形重合.
2、如图(2),可以看作由旋转______次生成的,每次旋转的度数是_______.
3、 ①找出各图形的旋转中心,并分别用字母A、B、C、D表示;
②正三角形绕其旋转中心最少旋转_________度,所得图形与原图重合;
正四边形绕其旋转中心最少旋转_________度,所得图形与原图重合;
正五边形绕其旋转中心最少旋转_________度,所得图形与原图重合;
正六边形绕其旋转中心最少旋转_________度,所得图形与原图重合;
③由②中的结论,你可以总结出规律________________________________________.
4、请你设计一个旋转40°后可以与原图重合的旋转对称图形.
五:课堂测试达标
1、下列是旋转对称图形的是 ( )
①电风扇;②家庭用的剪子;③机械上的齿轮;④国旗上的一个五角星
A.①②③ B.②③④ C.①③④ D.①②④
2、如图所示,不是旋转对称图形的有 ( )
A.0个 B.1个 C.2个 D.3个
3、正六边形绕其旋转中心旋转旋转m度后可以与原图形重合,则m的值不能是( )
A.300 B.150 C.120 D.180
4、在下列多边形中,旋转10°、20°、30°……90°、180°都能与原图重合的是 ( )
A. 正方形 B.正十边形 C.正二十边形 D.正三十六边形
5、五角星绕其旋转中心最少旋转___________后才能与自身重合.
.
6、如图,可以看作是由 旋转_____次生成的,每次旋转的度数是______.
7、如图1,绕其旋转中心最少旋转_________度,即可与原图重合.
如图2,绕其旋转中心最少旋转_________度,即可与原图重合.
8、给出下列图形:①线段;②平行四边形;③等边三角形;④长方形;⑤正方形⑥120°的角. 其中,轴对称图形有________;旋转对称图形有________.
9、如图,扇形AOB的度数为,四边形OCDE是边长为1的正方形,
点C、E、D分别在OA、OB、及弧AB上,过A作AF⊥ED交ED的
延长线于点F,那么图中阴影部分的面积为 .
10、如图,是一个边长为4米的正六边形喷水池,请你设计一个方案:
在池中安装13盏灯,使得相临两盏灯之间的距离在1米到2米
之间,请用点表示每一盏灯,画出你的设计方案.
六:畅所欲言
本节课你学到了什么?
① ② ③ ④
第 2题 第3题
(1) (2) (3) (4)
O
(1) (2) (3)
(1) (2)
班级 姓名 2011年11月20日
学习目标:1.进一步巩固图形的平移、旋转等概念,并能运用相关知识解决问题;
2.理解旋转对称图形的概念,能够熟练判断图形是否旋转对称图形,能够说出旋转对称图形形成的过程.
学习重点:旋转对称图形的概念.
学习难点:综合运用变换知识解决有关问题.
学习过程:
一、课前练习
1下列 几面国旗中是轴对称图形的有( )
A.B. C. D.
2.如图,分别将△ABC绕点A顺时针旋转90°、180°、270°,画出图形,所得图形与△ABC组成的图形是________.
3.分析下图中①,②, ③中阴影部分的分布规律,按此规律在下图④中画出其中的阴影部分:
二、新课学习:
1.(1)观察图1,若将图1看作两部分,将阴影部分绕点O旋转_________°,可与空白部分重合;若将图1看作整体,则将图1绕点________至少旋转________°,可与原图重合.
(2)若将图2看作整体,则将图2绕点________至少旋转________°,可与原图重合.
(3)若将图3看作整体,则将图3绕点________至少旋转________°,可与原图重合.
(4)若将图4看作整体,则将图4绕点________至少旋转________°,可与原图重合.
结论:旋转对称图形的特征_______________________________________________.
以上图形中,_________________________是旋转对称图形.
比较:轴对称图形与旋转对称图形有何异同?
(1)相同点:
(2)不同点:
三应用迁移:
例1 如图11-2-12所示的旋转对称图形中,各图形围绕其旋转中心最少需要旋转多少度之后,能够与它的自身重合?
同类变式1 如图11-2-13中的几个图标是著名银行的标志,你能指出其中不是旋转对称图形的图标吗?( )
同类变式2 如图11-2-14旋转对称图形的个数是( )
A.1 B.2 C.3 D.4
你有什么体会?把你的想法与大家交流一下。
巩固拓展:
1如图(1),在图中标出旋转中心,并用点O表示,该图形绕点O最少旋转__________
度所得图形与原图形重合.
2、如图(2),可以看作由旋转______次生成的,每次旋转的度数是_______.
3、 ①找出各图形的旋转中心,并分别用字母A、B、C、D表示;
②正三角形绕其旋转中心最少旋转_________度,所得图形与原图重合;
正四边形绕其旋转中心最少旋转_________度,所得图形与原图重合;
正五边形绕其旋转中心最少旋转_________度,所得图形与原图重合;
正六边形绕其旋转中心最少旋转_________度,所得图形与原图重合;
③由②中的结论,你可以总结出规律________________________________________.
4、请你设计一个旋转40°后可以与原图重合的旋转对称图形.
五:课堂测试达标
1、下列是旋转对称图形的是 ( )
①电风扇;②家庭用的剪子;③机械上的齿轮;④国旗上的一个五角星
A.①②③ B.②③④ C.①③④ D.①②④
2、如图所示,不是旋转对称图形的有 ( )
A.0个 B.1个 C.2个 D.3个
3、正六边形绕其旋转中心旋转旋转m度后可以与原图形重合,则m的值不能是( )
A.300 B.150 C.120 D.180
4、在下列多边形中,旋转10°、20°、30°……90°、180°都能与原图重合的是 ( )
A. 正方形 B.正十边形 C.正二十边形 D.正三十六边形
5、五角星绕其旋转中心最少旋转___________后才能与自身重合.
.
6、如图,可以看作是由 旋转_____次生成的,每次旋转的度数是______.
7、如图1,绕其旋转中心最少旋转_________度,即可与原图重合.
如图2,绕其旋转中心最少旋转_________度,即可与原图重合.
8、给出下列图形:①线段;②平行四边形;③等边三角形;④长方形;⑤正方形⑥120°的角. 其中,轴对称图形有________;旋转对称图形有________.
9、如图,扇形AOB的度数为,四边形OCDE是边长为1的正方形,
点C、E、D分别在OA、OB、及弧AB上,过A作AF⊥ED交ED的
延长线于点F,那么图中阴影部分的面积为 .
10、如图,是一个边长为4米的正六边形喷水池,请你设计一个方案:
在池中安装13盏灯,使得相临两盏灯之间的距离在1米到2米
之间,请用点表示每一盏灯,画出你的设计方案.
六:畅所欲言
本节课你学到了什么?
① ② ③ ④
第 2题 第3题
(1) (2) (3) (4)
O
(1) (2) (3)
(1) (2)
