2020-2021学年八年级数学人教版下册第十八章《平行四边形》培优练习(五)(word版含解析)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册第十八章《平行四边形》培优练习(五)(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 206.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-27 00:00:00 | ||
图片预览


文档简介
八年级下册第十八章《平行四边形》
培优练习(五)
1.如图,四边形AOBC为正方形,E为AC的中点,连接OE,OE=.
(1)求点C的坐标;
(2)F为AC上一点,∠FOB=2∠AOE,
①求点F的坐标;
②作点A关于OF的对称点H,连接AH和BH,则∠AHB的度数为
;BH的长度为
.(直接写出结果)
2.如图,在?ABCD中,对角线AC,BD交于点O,E是AD上一点,连接EO并延长,交BC于点F.连接AF,CE,EF平分∠AEC.
(1)求证:四边形AFCE是菱形;
(2)若∠DAC=60°,AC=2,求四边形AFCE的面积.
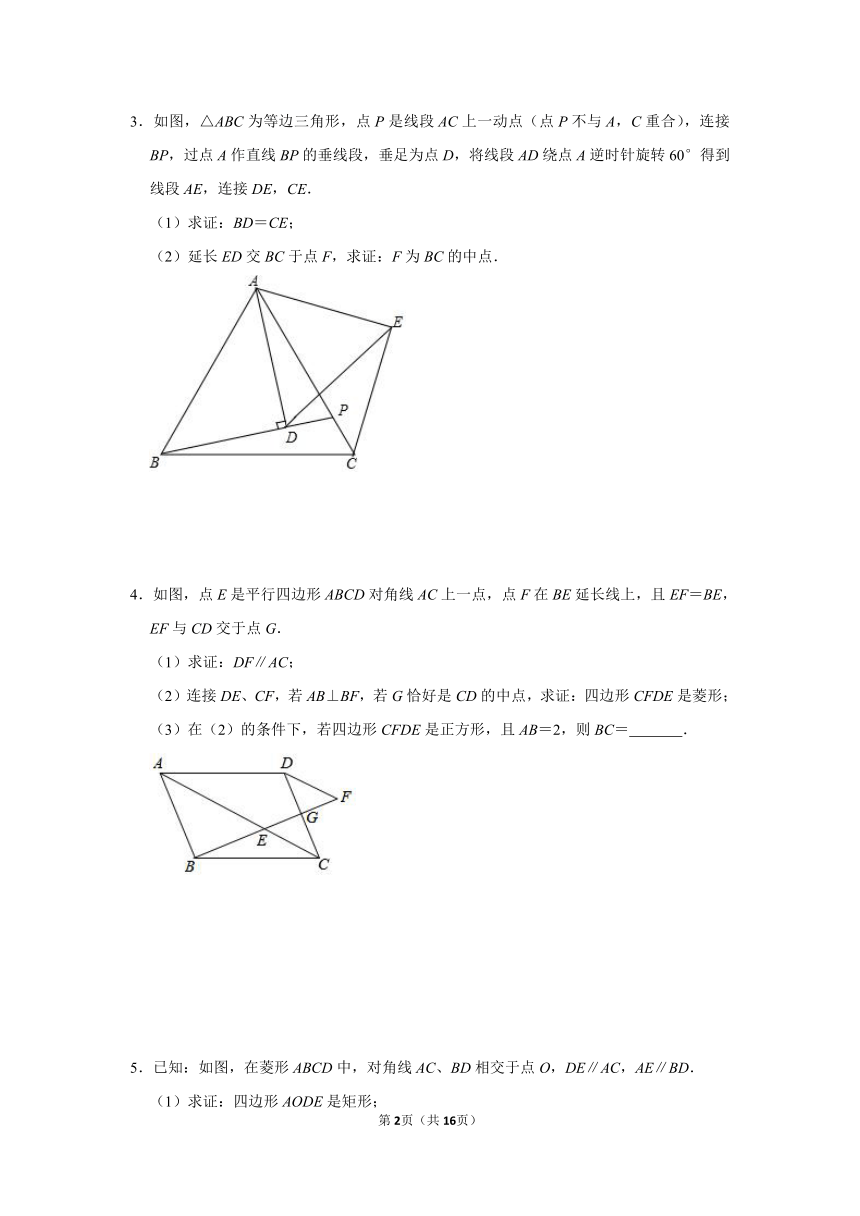
3.如图,△ABC为等边三角形,点P是线段AC上一动点(点P不与A,C重合),连接BP,过点A作直线BP的垂线段,垂足为点D,将线段AD绕点A逆时针旋转60°得到线段AE,连接DE,CE.
(1)求证:BD=CE;
(2)延长ED交BC于点F,求证:F为BC的中点.
4.如图,点E是平行四边形ABCD对角线AC上一点,点F在BE延长线上,且EF=BE,EF与CD交于点G.
(1)求证:DF∥AC;
(2)连接DE、CF,若AB⊥BF,若G恰好是CD的中点,求证:四边形CFDE是菱形;
(3)在(2)的条件下,若四边形CFDE是正方形,且AB=2,则BC=
.
5.已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=4,∠BCD=120°,求菱形ABCD的面积.
6.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=OC,连接CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为4,∠ABC=60°,求AE的长.
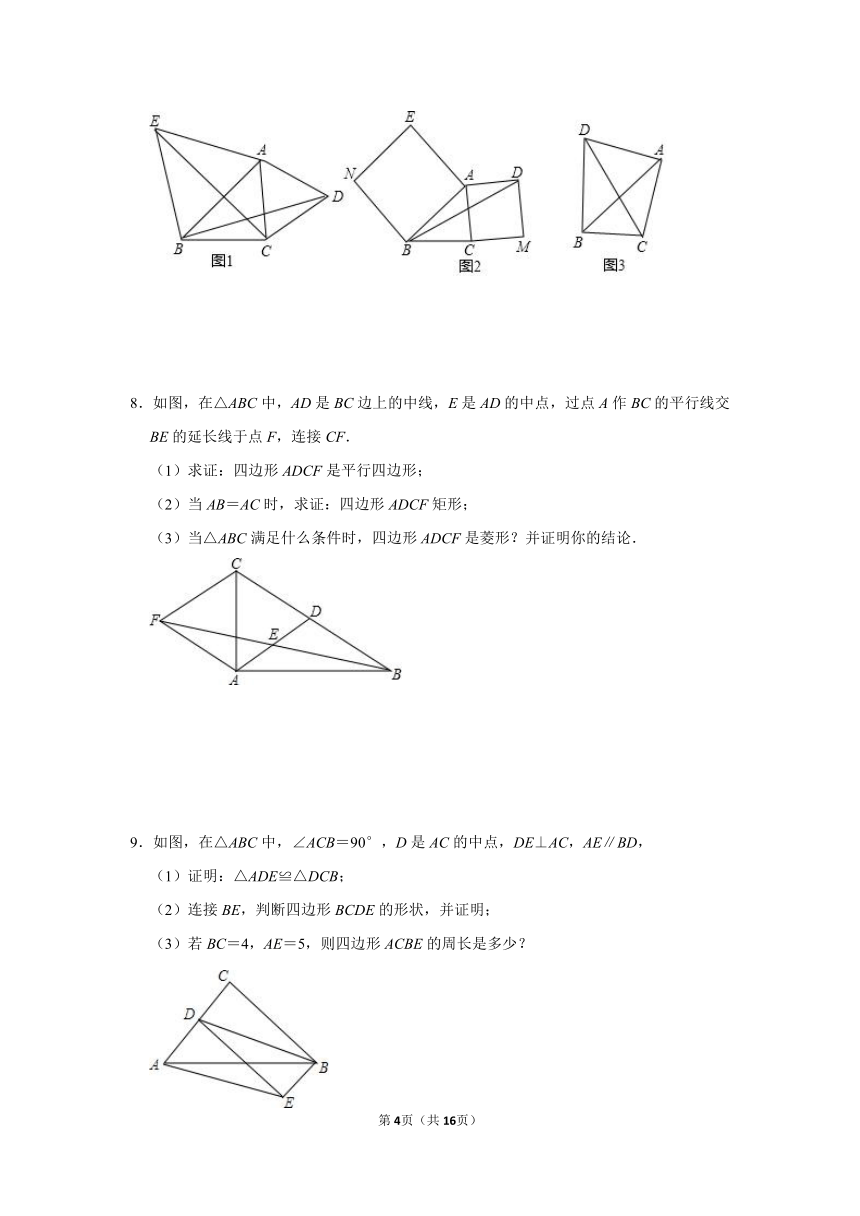
7.(1)如图1,锐角△ABC中,分别以AB、AC为边向外作等边△ABE和等边△ACD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.
【深入探究】
(2)如图2,△ABC中,∠ABC=45°,AB=5cm,BC=3cm,分别以AB、AC为边向外作正方形ABNE和正方形ACMD,连接BD,求BD的长.
(3)如图3,在(2)的条件下,以AC为直角边在线段AC的左侧作等腰直角△ACD,求BD的长.
8.如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:四边形ADCF是平行四边形;
(2)当AB=AC时,求证:四边形ADCF矩形;
(3)当△ABC满足什么条件时,四边形ADCF是菱形?并证明你的结论.
9.如图,在△ABC中,∠ACB=90°,D是AC的中点,DE⊥AC,AE∥BD,
(1)证明:△ADE≌△DCB;
(2)连接BE,判断四边形BCDE的形状,并证明;
(3)若BC=4,AE=5,则四边形ACBE的周长是多少?
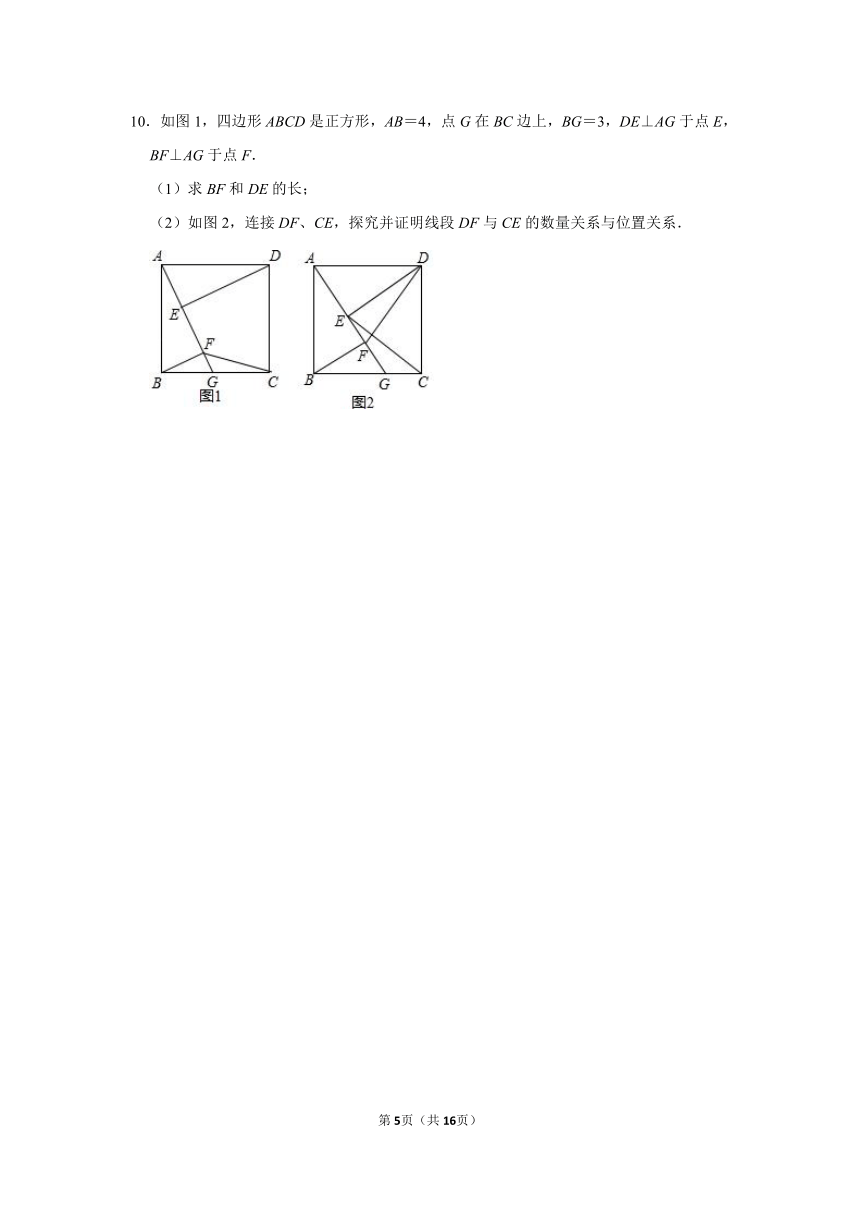
10.如图1,四边形ABCD是正方形,AB=4,点G在BC边上,BG=3,DE⊥AG于点E,BF⊥AG于点F.
(1)求BF和DE的长;
(2)如图2,连接DF、CE,探究并证明线段DF与CE的数量关系与位置关系.
参考答案
1.解:(1)∵四边形AOBC为正方形,
∴OA=AC=CB=BO,∠OAC=∠ACB=∠CBO=∠BOA=90°,
∵E为AC的中点,
∴AE=EC=x,则AC=AO=2x,
在Rt△AOE中:,解得:x=1,
∴OA=AC=2,
∴C(2,2).
(2)①取BC中点M,延长OM交AC延长线于点N,
∵OA=OB,∠OAE=∠OBM,AE=BM,
∴△AOE≌△OBM(SAS),
∴∠AOE=∠BOM
又∵∠FOB=2∠AOE,
∴∠FOM=∠BOM=∠AOE,
又∵CN∥OB,
∴∠BOM=∠CNM,
∴∠FOM=∠FNO,
∴FO=FN,
∵BM=MC,∠MCN=∠MBO=90°,∠BOM=∠CNM,
∴△CMN≌△BMO(AAS),
∴CN=OB=2,
设CF=x,则AF=2﹣x,NF=2+x=FO,
在Rt△AOF中:AF2+AO2=OF2,
∴(2﹣x)2+22=(2+x)2,解得:x=0.5,
∴F(1.5,2).
②如图2,连接OH,AB,则AB=AC=2.
∵A与H关于AF对称,
∴∠AOF=∠HOF,OH=OA=OB,OF垂直平分AH,
作OP⊥BH于P,则∠BOP=∠HOP,
∵∠AOH+∠BOH=∠AOB=90°,
∴∠FOP=45°,
∵∠OQH=∠OPH=90°,
∴∠AHB=180°﹣∠FOP=135°,
∵F(1.5,2),
∴AF=1.5,
∴OF=2.5,
∴AH=2AQ===,
作BN⊥AH于N,则∠BHN=∠HBN=45°,
∴BN=HN=x,
∴BH=x,AN=AH+HN=+x,
在Rt△ANB中:AB2=AN2+BN2,
∴8=+x2,解得,(舍),
∴BH=.
2.(1)证明:∵四边形ABCD是平行四边形
∴AD∥BC,AO=CO,
∴∠AEF=∠CFE,
在△AOE和△COF中,,
∴△AOE≌△COF(AAS),
∴OF=OE,
∵AO=CO,
∴四边形AFCE是平行四边形;
∵EF平分∠AEC,
∴∠AEF=∠CEF,
∴∠CFE=∠CEF,
∴CE=CF,
∴四边形AFCE是菱形;
(2)解:由(1)得:四边形AFCE是菱形,
∴AC⊥EF,AO=CO=AC=1,
∴∠AOE=90°,
∵∠DAC=60°,
∴∠AEO=30°,
∴OE=AO=,
∴EF=2OE=2,
∴四边形AFCE的面积=AC×EF=×2×2=2.
3.(1)证明:∵线段AD绕点A逆时针旋转60°得到线段AE,
∴△ADE是等边三角形,
在等边△ABC和等边△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=CE.
(2)证明:如图,过点C作CG∥BP交DF的延长线于点G.
∴∠G=∠BDF,
∵∠ADE=60°,∠ADB=90°,
∴∠BDF=30°,
∴∠G=30°,
由(1)可知,BD=CE,∠CEA=∠BDA,
∵AD⊥BP,
∴∠BDA=90°,
∴∠CEA=90°,
∵∠AED=60°,
∴∠CED=30°=∠G,
∴CE=CG,
∴BD=CG,
在△BDF和△CGF中,
,
∴△BDF≌△CGF(AAS),
∴BF=FC,
即F为BC的中点.
4.(1)证明:连接BD,交AC于点O,如图所示:
∵四边形ABCD是平行四边形,
∴BO=DO,
∵BE=EF,
∴OE是△BDF的中位线,
∴OE∥DF,即DF∥AC;
(2)证明:如图所示:
由(1)得:DF∥AC,
∴∠F=∠CEG,∠GDF=∠GCE,
∵G是CD的中点,
∴DG=CG,
∴△DFG≌△CEG(AAS),
∴FG=EG,
∴四边形CFDE是平行四边形,
∵四边形ABCD是平行四边形,
∴AB∥CD,
又∵AB⊥BF,
∴CD⊥BF,
∴平行四边形CFDE是菱形;
(3)解:∵四边形ABCD是平行四边形,
∴BC=AD,CD=AB=2,
∵四边形CFDE是正方形,
∴DE=CE=CD=,BE=EF=CD=2,∠DEC=90°,
∴∠AED=90°,
∵AB⊥BF,
∴∠ABE=90°,
∴AE===2,
∴AD===,
∴BC=,
故答案为:.
5.(1)证明:∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∵在菱形ABCD中,AC⊥BD,
∴∠AOD=90°,
∴四边形AODE是矩形;
(2)∵∠BCD=120°,AB∥CD,
∴∠ABC=180°﹣120°=60°,
∵AB=BC=AC,
∴△ABC是等边三角形,
∴OA=×4=2,OB=,
∵四边形ABCD是菱形,
∴四边形ABCD的面积=.
6.(1)证明:∵DE=OC,DE∥AC,
∴四边形OCED是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠COD=90°,
∴平行四边形OCED是矩形.
∴OE=CD.
(2)解:在菱形ABCD中,∠ABC=60°,
∴AC=AB=4,
∴在矩形OCED中,CE=OD==2,
∴在△ACE中,AE==2.
7.解:(1)BD=CE,
理由是:∵△ABE和△ACD是等边三角形,
∴AE=AB,AC=AD,∠BAE=∠CAD=60°,
∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD,
在△EAC和△BAD中,
,
∴△EAC≌△BAD(SAS)
∴BD=CE;
(2)如图2,连接EB、EC,
∵四边形ACMD和四边形ABNE是正方形,
∴AE=AB,AD=AC,∠EAB=∠DAC=90°
∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD,
在△EAC和△BAD中,
,
∴△EAC≌△BAD,
∴BD=CE.
∵∠EBA=∠ABC=45°
∴∠EBC=90°
∵AE=AB=5,∠EAB=90°,
∴BE=5,
∵BC=3
∴EC===,
∴BD=EC=;
(3)如图3,在线段AC的右侧过点A作AE⊥AB于点A,交BC的延长线于点E,连接BE.
∵AE⊥AB,
∴∠BAE=90°,
又∵∠ABC=45°,
∴∠E=∠ABC=45°,
∴AE=AB=5,BE=5,
又∵∠BAE=∠DAC=90°,
∴∠BAE﹣∠BAC=∠DAC﹣∠BAC,即∠EAC=∠BAD,
在△EAC和△BAD中,
,
∴△EAC≌△BAD,
∴BD=CE,
∵BC=3,
∴BD=CE=(5﹣3)cm.
8.解:
(1)证明:∵AF∥BC,
∴∠FAE=∠EDB,∠AFE=∠EBD.
∵E是AD的中点,
∴AE=DE,
在△AEF和△DEB中,
,
∴△AEF≌△DEB(AAS),
∴AF=DB,
又∵BD=DC,
∴AF=DC,
∴四边形ADCF为平行四边形;
(2)证明:∵AB=AC,且AD为BC边上的中线,
∴AD⊥CD,
即∠ADB=90°,
∴四边形ADCF为矩形;
(3)解:当△ABC满足∠BAC=90°时,则四边形ADCF是菱形,
理由如下:
∵∠BAC=90°,AD是BC边的中线,
∴AD=DC=BC,
又∵四边形ADCF为平行四边形,
∴四边形ADCF是菱形.
9.(1)证明:∵AE∥BD,
∴∠CDB=∠DAE,
∵∠ACB=90°,DE⊥AC,
∴∠C=∠ADE=90°,
∴DE∥BC,
∵D为AC中点,
∴AD=CD,
在△ADE和△DCB中,,
∴△ADE≌△DCB(ASA);
(2)解:四边形BCDE是矩形;理由如下:
由(1)得:△ADE≌△DCB,
∴DE=BC=4,BD=AE=5,
又∵∠ACB=90°,DE⊥AC,
∴DE∥BC,
∴四边形BCDE是矩形;
(3)解:在Rt△DCB中,BC=4,BD=5,
由勾股定理得:CD==3,
∴AD=CD=3,
∵四边形BCDE是矩形,
∴CD=BE=3,
∴四边形ACBE的周长是AC+BC+BE+AE=3+3+4+3+5=18.
10.解:(1)如图1,
∵四边形ABCD是正方形,
∴AD=AB=4,∠BAD=90°,
∵DE⊥AG,BF⊥AG,
∴∠AED=∠BFA=90°,
在Rt△ABG中,AG==5,
∵?AG?BF=?AB?BG,
∴BF==,
∴AF===,
∵∠BAF+∠ABF=90°,∠BAF+∠DAE=90°,
∴∠ABF=∠DAE,
在△ABF和△DAE中
,
∴△ABF≌△DAE,
∴DE=AF=;
(2)DF=CE,DF⊥CE.理由如下:
作CH⊥DE于H,如图2,
∵△ABF≌△DAE,
∴AE=BF=,
∴EF=AF﹣AE=,
与(1)的证明方法一样可得△CDH≌△DAE,
∴CH=DE=,DH=AE=,
∴EH=DE﹣DH=,
∴EH=EF,
在△DEF和△CHE中
,
∴△DEF≌△CHE,
∴DF=CE,∠EDF=∠HCE,
∵∠1=∠2,
∴∠3=∠CHD=90°,
∴DF⊥CE.
第1页(共1页)
培优练习(五)
1.如图,四边形AOBC为正方形,E为AC的中点,连接OE,OE=.
(1)求点C的坐标;
(2)F为AC上一点,∠FOB=2∠AOE,
①求点F的坐标;
②作点A关于OF的对称点H,连接AH和BH,则∠AHB的度数为
;BH的长度为
.(直接写出结果)
2.如图,在?ABCD中,对角线AC,BD交于点O,E是AD上一点,连接EO并延长,交BC于点F.连接AF,CE,EF平分∠AEC.
(1)求证:四边形AFCE是菱形;
(2)若∠DAC=60°,AC=2,求四边形AFCE的面积.
3.如图,△ABC为等边三角形,点P是线段AC上一动点(点P不与A,C重合),连接BP,过点A作直线BP的垂线段,垂足为点D,将线段AD绕点A逆时针旋转60°得到线段AE,连接DE,CE.
(1)求证:BD=CE;
(2)延长ED交BC于点F,求证:F为BC的中点.
4.如图,点E是平行四边形ABCD对角线AC上一点,点F在BE延长线上,且EF=BE,EF与CD交于点G.
(1)求证:DF∥AC;
(2)连接DE、CF,若AB⊥BF,若G恰好是CD的中点,求证:四边形CFDE是菱形;
(3)在(2)的条件下,若四边形CFDE是正方形,且AB=2,则BC=
.
5.已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=4,∠BCD=120°,求菱形ABCD的面积.
6.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=OC,连接CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为4,∠ABC=60°,求AE的长.
7.(1)如图1,锐角△ABC中,分别以AB、AC为边向外作等边△ABE和等边△ACD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.
【深入探究】
(2)如图2,△ABC中,∠ABC=45°,AB=5cm,BC=3cm,分别以AB、AC为边向外作正方形ABNE和正方形ACMD,连接BD,求BD的长.
(3)如图3,在(2)的条件下,以AC为直角边在线段AC的左侧作等腰直角△ACD,求BD的长.
8.如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:四边形ADCF是平行四边形;
(2)当AB=AC时,求证:四边形ADCF矩形;
(3)当△ABC满足什么条件时,四边形ADCF是菱形?并证明你的结论.
9.如图,在△ABC中,∠ACB=90°,D是AC的中点,DE⊥AC,AE∥BD,
(1)证明:△ADE≌△DCB;
(2)连接BE,判断四边形BCDE的形状,并证明;
(3)若BC=4,AE=5,则四边形ACBE的周长是多少?
10.如图1,四边形ABCD是正方形,AB=4,点G在BC边上,BG=3,DE⊥AG于点E,BF⊥AG于点F.
(1)求BF和DE的长;
(2)如图2,连接DF、CE,探究并证明线段DF与CE的数量关系与位置关系.
参考答案
1.解:(1)∵四边形AOBC为正方形,
∴OA=AC=CB=BO,∠OAC=∠ACB=∠CBO=∠BOA=90°,
∵E为AC的中点,
∴AE=EC=x,则AC=AO=2x,
在Rt△AOE中:,解得:x=1,
∴OA=AC=2,
∴C(2,2).
(2)①取BC中点M,延长OM交AC延长线于点N,
∵OA=OB,∠OAE=∠OBM,AE=BM,
∴△AOE≌△OBM(SAS),
∴∠AOE=∠BOM
又∵∠FOB=2∠AOE,
∴∠FOM=∠BOM=∠AOE,
又∵CN∥OB,
∴∠BOM=∠CNM,
∴∠FOM=∠FNO,
∴FO=FN,
∵BM=MC,∠MCN=∠MBO=90°,∠BOM=∠CNM,
∴△CMN≌△BMO(AAS),
∴CN=OB=2,
设CF=x,则AF=2﹣x,NF=2+x=FO,
在Rt△AOF中:AF2+AO2=OF2,
∴(2﹣x)2+22=(2+x)2,解得:x=0.5,
∴F(1.5,2).
②如图2,连接OH,AB,则AB=AC=2.
∵A与H关于AF对称,
∴∠AOF=∠HOF,OH=OA=OB,OF垂直平分AH,
作OP⊥BH于P,则∠BOP=∠HOP,
∵∠AOH+∠BOH=∠AOB=90°,
∴∠FOP=45°,
∵∠OQH=∠OPH=90°,
∴∠AHB=180°﹣∠FOP=135°,
∵F(1.5,2),
∴AF=1.5,
∴OF=2.5,
∴AH=2AQ===,
作BN⊥AH于N,则∠BHN=∠HBN=45°,
∴BN=HN=x,
∴BH=x,AN=AH+HN=+x,
在Rt△ANB中:AB2=AN2+BN2,
∴8=+x2,解得,(舍),
∴BH=.
2.(1)证明:∵四边形ABCD是平行四边形
∴AD∥BC,AO=CO,
∴∠AEF=∠CFE,
在△AOE和△COF中,,
∴△AOE≌△COF(AAS),
∴OF=OE,
∵AO=CO,
∴四边形AFCE是平行四边形;
∵EF平分∠AEC,
∴∠AEF=∠CEF,
∴∠CFE=∠CEF,
∴CE=CF,
∴四边形AFCE是菱形;
(2)解:由(1)得:四边形AFCE是菱形,
∴AC⊥EF,AO=CO=AC=1,
∴∠AOE=90°,
∵∠DAC=60°,
∴∠AEO=30°,
∴OE=AO=,
∴EF=2OE=2,
∴四边形AFCE的面积=AC×EF=×2×2=2.
3.(1)证明:∵线段AD绕点A逆时针旋转60°得到线段AE,
∴△ADE是等边三角形,
在等边△ABC和等边△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=CE.
(2)证明:如图,过点C作CG∥BP交DF的延长线于点G.
∴∠G=∠BDF,
∵∠ADE=60°,∠ADB=90°,
∴∠BDF=30°,
∴∠G=30°,
由(1)可知,BD=CE,∠CEA=∠BDA,
∵AD⊥BP,
∴∠BDA=90°,
∴∠CEA=90°,
∵∠AED=60°,
∴∠CED=30°=∠G,
∴CE=CG,
∴BD=CG,
在△BDF和△CGF中,
,
∴△BDF≌△CGF(AAS),
∴BF=FC,
即F为BC的中点.
4.(1)证明:连接BD,交AC于点O,如图所示:
∵四边形ABCD是平行四边形,
∴BO=DO,
∵BE=EF,
∴OE是△BDF的中位线,
∴OE∥DF,即DF∥AC;
(2)证明:如图所示:
由(1)得:DF∥AC,
∴∠F=∠CEG,∠GDF=∠GCE,
∵G是CD的中点,
∴DG=CG,
∴△DFG≌△CEG(AAS),
∴FG=EG,
∴四边形CFDE是平行四边形,
∵四边形ABCD是平行四边形,
∴AB∥CD,
又∵AB⊥BF,
∴CD⊥BF,
∴平行四边形CFDE是菱形;
(3)解:∵四边形ABCD是平行四边形,
∴BC=AD,CD=AB=2,
∵四边形CFDE是正方形,
∴DE=CE=CD=,BE=EF=CD=2,∠DEC=90°,
∴∠AED=90°,
∵AB⊥BF,
∴∠ABE=90°,
∴AE===2,
∴AD===,
∴BC=,
故答案为:.
5.(1)证明:∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∵在菱形ABCD中,AC⊥BD,
∴∠AOD=90°,
∴四边形AODE是矩形;
(2)∵∠BCD=120°,AB∥CD,
∴∠ABC=180°﹣120°=60°,
∵AB=BC=AC,
∴△ABC是等边三角形,
∴OA=×4=2,OB=,
∵四边形ABCD是菱形,
∴四边形ABCD的面积=.
6.(1)证明:∵DE=OC,DE∥AC,
∴四边形OCED是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠COD=90°,
∴平行四边形OCED是矩形.
∴OE=CD.
(2)解:在菱形ABCD中,∠ABC=60°,
∴AC=AB=4,
∴在矩形OCED中,CE=OD==2,
∴在△ACE中,AE==2.
7.解:(1)BD=CE,
理由是:∵△ABE和△ACD是等边三角形,
∴AE=AB,AC=AD,∠BAE=∠CAD=60°,
∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD,
在△EAC和△BAD中,
,
∴△EAC≌△BAD(SAS)
∴BD=CE;
(2)如图2,连接EB、EC,
∵四边形ACMD和四边形ABNE是正方形,
∴AE=AB,AD=AC,∠EAB=∠DAC=90°
∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD,
在△EAC和△BAD中,
,
∴△EAC≌△BAD,
∴BD=CE.
∵∠EBA=∠ABC=45°
∴∠EBC=90°
∵AE=AB=5,∠EAB=90°,
∴BE=5,
∵BC=3
∴EC===,
∴BD=EC=;
(3)如图3,在线段AC的右侧过点A作AE⊥AB于点A,交BC的延长线于点E,连接BE.
∵AE⊥AB,
∴∠BAE=90°,
又∵∠ABC=45°,
∴∠E=∠ABC=45°,
∴AE=AB=5,BE=5,
又∵∠BAE=∠DAC=90°,
∴∠BAE﹣∠BAC=∠DAC﹣∠BAC,即∠EAC=∠BAD,
在△EAC和△BAD中,
,
∴△EAC≌△BAD,
∴BD=CE,
∵BC=3,
∴BD=CE=(5﹣3)cm.
8.解:
(1)证明:∵AF∥BC,
∴∠FAE=∠EDB,∠AFE=∠EBD.
∵E是AD的中点,
∴AE=DE,
在△AEF和△DEB中,
,
∴△AEF≌△DEB(AAS),
∴AF=DB,
又∵BD=DC,
∴AF=DC,
∴四边形ADCF为平行四边形;
(2)证明:∵AB=AC,且AD为BC边上的中线,
∴AD⊥CD,
即∠ADB=90°,
∴四边形ADCF为矩形;
(3)解:当△ABC满足∠BAC=90°时,则四边形ADCF是菱形,
理由如下:
∵∠BAC=90°,AD是BC边的中线,
∴AD=DC=BC,
又∵四边形ADCF为平行四边形,
∴四边形ADCF是菱形.
9.(1)证明:∵AE∥BD,
∴∠CDB=∠DAE,
∵∠ACB=90°,DE⊥AC,
∴∠C=∠ADE=90°,
∴DE∥BC,
∵D为AC中点,
∴AD=CD,
在△ADE和△DCB中,,
∴△ADE≌△DCB(ASA);
(2)解:四边形BCDE是矩形;理由如下:
由(1)得:△ADE≌△DCB,
∴DE=BC=4,BD=AE=5,
又∵∠ACB=90°,DE⊥AC,
∴DE∥BC,
∴四边形BCDE是矩形;
(3)解:在Rt△DCB中,BC=4,BD=5,
由勾股定理得:CD==3,
∴AD=CD=3,
∵四边形BCDE是矩形,
∴CD=BE=3,
∴四边形ACBE的周长是AC+BC+BE+AE=3+3+4+3+5=18.
10.解:(1)如图1,
∵四边形ABCD是正方形,
∴AD=AB=4,∠BAD=90°,
∵DE⊥AG,BF⊥AG,
∴∠AED=∠BFA=90°,
在Rt△ABG中,AG==5,
∵?AG?BF=?AB?BG,
∴BF==,
∴AF===,
∵∠BAF+∠ABF=90°,∠BAF+∠DAE=90°,
∴∠ABF=∠DAE,
在△ABF和△DAE中
,
∴△ABF≌△DAE,
∴DE=AF=;
(2)DF=CE,DF⊥CE.理由如下:
作CH⊥DE于H,如图2,
∵△ABF≌△DAE,
∴AE=BF=,
∴EF=AF﹣AE=,
与(1)的证明方法一样可得△CDH≌△DAE,
∴CH=DE=,DH=AE=,
∴EH=DE﹣DH=,
∴EH=EF,
在△DEF和△CHE中
,
∴△DEF≌△CHE,
∴DF=CE,∠EDF=∠HCE,
∵∠1=∠2,
∴∠3=∠CHD=90°,
∴DF⊥CE.
第1页(共1页)
