2020-2021学年人教版九年级下册26.1.2反比例函数的图象和性质课件(18张)
文档属性
| 名称 | 2020-2021学年人教版九年级下册26.1.2反比例函数的图象和性质课件(18张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 226.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-27 00:00:00 | ||
图片预览




文档简介
26.1.2 反比例函数的图象和性质
人 教 版 九 年 级 数 学 下 册 《 第 二 十 六 章 反 比 例 函 数 》
九 下 数 学 课 堂
反比例函数
本课学习目标:
1.会画反比例函数的图象,理解反比例函数的图象和性质.
2.感悟“数形结合”、“变化与对应”和“转化”的数学思想,并能应用数形结合和转化思想根据反比例函数的图象探究其性质.
3.能够初步应用反比例函数的图象和性质解决问题.
九 下 数 学 课 堂
反比例函数
一、问题引入,认识新知
问题 1 正比例函数的图象是什么样的?它有哪些性质?我们是如何研究的?
{5940675A-B579-460E-94D1-54222C63F5DA}函数
图象形状
所在象限
变化趋势
函数的增减性
一条直线
一条直线
一、三象限
二、四象限
从左向右
上升
y 随 x 的增大而增大
从左向右
下降
y 随 x 的增大而减小
研究方法:画出图象,观察,猜想 ,验证.
反比例函数
九 下 数 学 课 堂
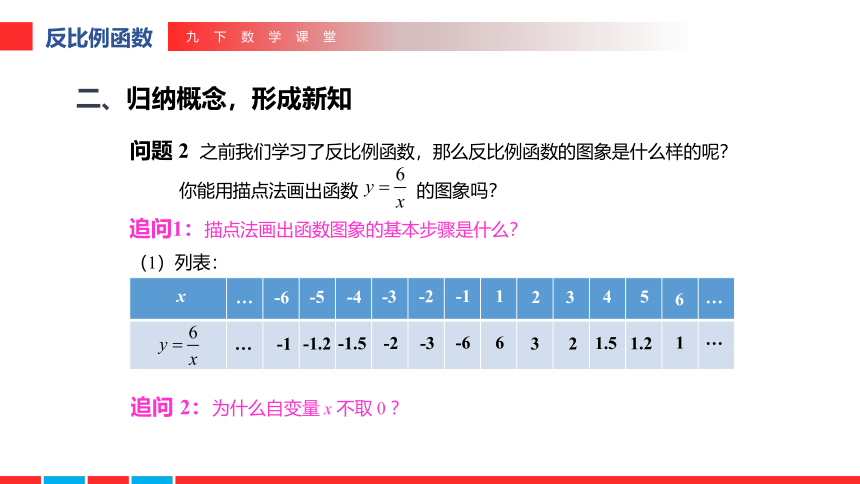
问题 2 之前我们学习了反比例函数,那么反比例函数的图象是什么样的呢?
你能用描点法画出函数 的图象吗?
追问 2:为什么自变量 x 不取 0 ?
{7DF18680-E054-41AD-8BC1-D1AEF772440D}
x
1
-1
-2
-3
-4
-5
-6
…
6
5
4
3
2
…
6
-6
-3
-2
-1.5
-1.2
-1
…
1
1.2
1.5
2
3
…
追问1:描点法画出函数图象的基本步骤是什么?
(1)列表:
二、归纳概念,形成新知
反比例函数
九 下 数 学 课 堂
-4
-6
-2
-4
-6
-2
O
{7DF18680-E054-41AD-8BC1-D1AEF772440D}
x
-1
-2
-3
-4
-5
-6
…
-6
-3
-2
-1.5
-1
…
(2)描点:
{7DF18680-E054-41AD-8BC1-D1AEF772440D}
1
6
5
4
3
2
…
6
1
1.5
2
3
…
x
反比例函数
九 下 数 学 课 堂
-4
-6
-2
-4
-6
-2
O
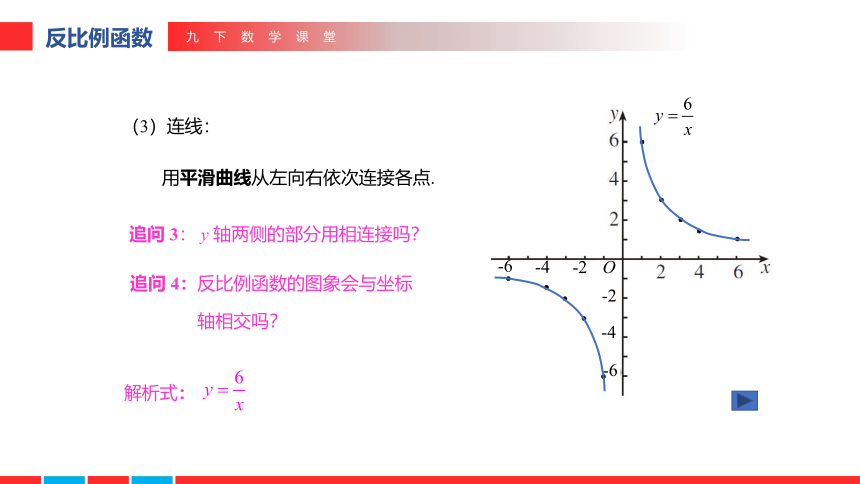
(3)连线:
用平滑曲线从左向右依次连接各点.
追问 3: y 轴两侧的部分用相连接吗?
追问 4:反比例函数的图象会与坐标
轴相交吗?
解析式:
反比例函数
九 下 数 学 课 堂
-4
-6
-2
-4
-6
-2
O
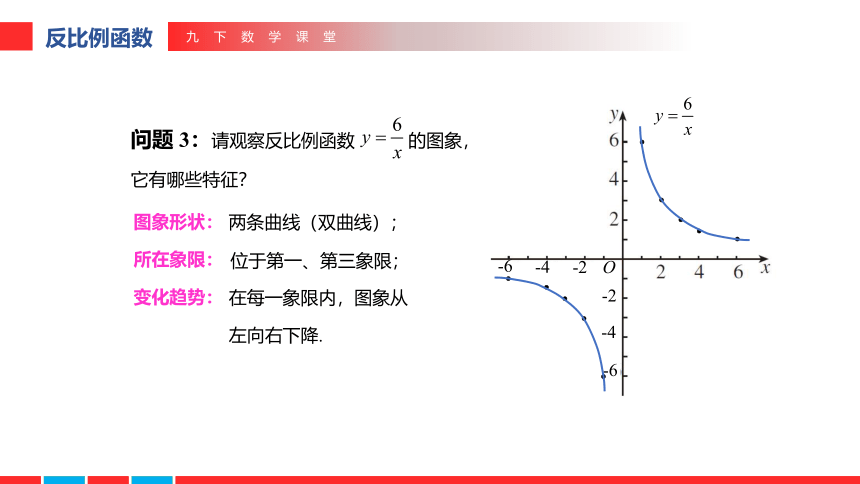
问题 3:请观察反比例函数 的图象,
它有哪些特征?
图象形状:
所在象限:
变化趋势:
两条曲线(双曲线);
位于第一、第三象限;
在每一象限内,图象从
左向右下降.
反比例函数
九 下 数 学 课 堂
-4
-6
-2
-4
-6
-2
O
问题 3:请观察反比例函数 的图象,
它有哪些特征?
当 x < 0 或 x > 0 时,y 随 x 的增大而减小.
追问 1: 你能根据图象的变化趋势得到反比例函数的性质吗?
反比例函数
九 下 数 学 课 堂
-4
-6
-2
-4
-6
-2
O
问题 3:请观察反比例函数 的图象,
它有哪些特征?
当 x < 0 或 x > 0 时,y 随 x 的增大而减小.
图象形状:
所在象限:
变化趋势:
函数的增减性:
两条曲线(双曲线);
位于第一、第三象限;
在每一象限内,图象从
左向右下降.
-4
-6
-2
-4
-6
-2
O
反比例函数
九 下 数 学 课 堂
问题 4:是不是所有的反比例函数的图象都
具有这样的特征呢?画出反比例函数
的图象,并说出它的图象特征.
图象形状:
所在象限:
变化趋势:
函数性质:
两条曲线(双曲线);
位于第二、第四象限;
在每一象限内,图象从左向右上升;
当 x < 0 或 x > 0 时,y 随 x 的增大而增大.
反比例函数
九 下 数 学 课 堂
问题 5:你能概括一下反比例函数的图象性质吗?
(1) 当 k > 0 时,双曲线的两支分别位于第一、第三象限,在每一个象限内,y 随 x 的增大而减小;
一般地,反比例函数 的图象是双曲线,
(2) 当 k < 0 时,双曲线的两支分别位于第二、第四象限,在每一个象限内,y 随 x 的增大而增大.
反比例函数
三、巩固提高,应用新知
九 下 数 学 课 堂
例 1 下列图象中,可以是反比例函数的图象的是( ).
C
反比例函数
九 下 数 学 课 堂
例 2 已知反比例函数 的图象如图所示,则 k 0,
且在图象的每一支上,y 随 x 的增大而 .
<
增大
例 3 已知反比例函数 的图象经过点(2,1),
则它的图象位于 象限,则 k 0 .
提示:因为函数图象经过点(2,1),即当 x=2 时,y=1 ,
所以 ,解得 k=2.
一、三
>
反比例函数
九 下 数 学 课 堂
例 4 已知反比例函数 的图象上有两点 A (x1, y1) 和 B (x2, y2) , 且
x1< x2 < 0 , 则 y1- y2 的值是( )
B
(A)正数
(B)负数
(C)非正数
(D)非负数
提示:当 k < 0 时,在每一个象限内,y 随 x 的增大而增大.
A
B
∵ x1< x2 < 0 ,∴ y1 < y2 ,即 y1 - y2 < 0.
反比例函数
四、归纳总结,提升新知
九 下 数 学 课 堂
回顾本课的学习,回答以下问题?
1. 反比例函数的图象有什么特征?
(1) 当 k > 0 时,双曲线的两支分别位于第一、第三象限,在每一个象限内,y 随 x 的增大而减小;
一般的,反比例函数 的图象是双曲线,
(2) 当 k < 0 时,双曲线的两支分别位于第二、第四象限,在每一个象限内,y 随 x 的增大而增大.
反比例函数
四、归纳总结,提升新知
九 下 数 学 课 堂
回顾本课的学习,回答以下问题?
2. 反比例函数有哪些性质?
3. 我们是如何研究反比例函数的图象与性质的?
(1) 当 k > 0 时,在 x < 0 或 x > 0 时,y 随 x 的增大而减小;
(2) 当 k < 0 时,在 x < 0 或 x > 0 时,y 随 x 的增大而增大.
描点绘图,观察图象、猜想结论、验证规律,注意数形结合解决问题;
探究函数的图象性质:图象的形状,图象所在位置,图象的变化趋势,以及函数的增减性等.
反比例函数
五、课后作业
教材 P8 页,习题 26.1 的第 3 题;
教材 P9 页,习题 26.1 的第 5 题、第 8 题.
九 下 数 学 课 堂
九 下 数 学 课 堂
反比例函数
谢 谢 观 看 !
人 教 版 九 年 级 数 学 下 册 《 第 二 十 六 章 反 比 例 函 数 》
九 下 数 学 课 堂
反比例函数
本课学习目标:
1.会画反比例函数的图象,理解反比例函数的图象和性质.
2.感悟“数形结合”、“变化与对应”和“转化”的数学思想,并能应用数形结合和转化思想根据反比例函数的图象探究其性质.
3.能够初步应用反比例函数的图象和性质解决问题.
九 下 数 学 课 堂
反比例函数
一、问题引入,认识新知
问题 1 正比例函数的图象是什么样的?它有哪些性质?我们是如何研究的?
{5940675A-B579-460E-94D1-54222C63F5DA}函数
图象形状
所在象限
变化趋势
函数的增减性
一条直线
一条直线
一、三象限
二、四象限
从左向右
上升
y 随 x 的增大而增大
从左向右
下降
y 随 x 的增大而减小
研究方法:画出图象,观察,猜想 ,验证.
反比例函数
九 下 数 学 课 堂
问题 2 之前我们学习了反比例函数,那么反比例函数的图象是什么样的呢?
你能用描点法画出函数 的图象吗?
追问 2:为什么自变量 x 不取 0 ?
{7DF18680-E054-41AD-8BC1-D1AEF772440D}
x
1
-1
-2
-3
-4
-5
-6
…
6
5
4
3
2
…
6
-6
-3
-2
-1.5
-1.2
-1
…
1
1.2
1.5
2
3
…
追问1:描点法画出函数图象的基本步骤是什么?
(1)列表:
二、归纳概念,形成新知
反比例函数
九 下 数 学 课 堂
-4
-6
-2
-4
-6
-2
O
{7DF18680-E054-41AD-8BC1-D1AEF772440D}
x
-1
-2
-3
-4
-5
-6
…
-6
-3
-2
-1.5
-1
…
(2)描点:
{7DF18680-E054-41AD-8BC1-D1AEF772440D}
1
6
5
4
3
2
…
6
1
1.5
2
3
…
x
反比例函数
九 下 数 学 课 堂
-4
-6
-2
-4
-6
-2
O
(3)连线:
用平滑曲线从左向右依次连接各点.
追问 3: y 轴两侧的部分用相连接吗?
追问 4:反比例函数的图象会与坐标
轴相交吗?
解析式:
反比例函数
九 下 数 学 课 堂
-4
-6
-2
-4
-6
-2
O
问题 3:请观察反比例函数 的图象,
它有哪些特征?
图象形状:
所在象限:
变化趋势:
两条曲线(双曲线);
位于第一、第三象限;
在每一象限内,图象从
左向右下降.
反比例函数
九 下 数 学 课 堂
-4
-6
-2
-4
-6
-2
O
问题 3:请观察反比例函数 的图象,
它有哪些特征?
当 x < 0 或 x > 0 时,y 随 x 的增大而减小.
追问 1: 你能根据图象的变化趋势得到反比例函数的性质吗?
反比例函数
九 下 数 学 课 堂
-4
-6
-2
-4
-6
-2
O
问题 3:请观察反比例函数 的图象,
它有哪些特征?
当 x < 0 或 x > 0 时,y 随 x 的增大而减小.
图象形状:
所在象限:
变化趋势:
函数的增减性:
两条曲线(双曲线);
位于第一、第三象限;
在每一象限内,图象从
左向右下降.
-4
-6
-2
-4
-6
-2
O
反比例函数
九 下 数 学 课 堂
问题 4:是不是所有的反比例函数的图象都
具有这样的特征呢?画出反比例函数
的图象,并说出它的图象特征.
图象形状:
所在象限:
变化趋势:
函数性质:
两条曲线(双曲线);
位于第二、第四象限;
在每一象限内,图象从左向右上升;
当 x < 0 或 x > 0 时,y 随 x 的增大而增大.
反比例函数
九 下 数 学 课 堂
问题 5:你能概括一下反比例函数的图象性质吗?
(1) 当 k > 0 时,双曲线的两支分别位于第一、第三象限,在每一个象限内,y 随 x 的增大而减小;
一般地,反比例函数 的图象是双曲线,
(2) 当 k < 0 时,双曲线的两支分别位于第二、第四象限,在每一个象限内,y 随 x 的增大而增大.
反比例函数
三、巩固提高,应用新知
九 下 数 学 课 堂
例 1 下列图象中,可以是反比例函数的图象的是( ).
C
反比例函数
九 下 数 学 课 堂
例 2 已知反比例函数 的图象如图所示,则 k 0,
且在图象的每一支上,y 随 x 的增大而 .
<
增大
例 3 已知反比例函数 的图象经过点(2,1),
则它的图象位于 象限,则 k 0 .
提示:因为函数图象经过点(2,1),即当 x=2 时,y=1 ,
所以 ,解得 k=2.
一、三
>
反比例函数
九 下 数 学 课 堂
例 4 已知反比例函数 的图象上有两点 A (x1, y1) 和 B (x2, y2) , 且
x1< x2 < 0 , 则 y1- y2 的值是( )
B
(A)正数
(B)负数
(C)非正数
(D)非负数
提示:当 k < 0 时,在每一个象限内,y 随 x 的增大而增大.
A
B
∵ x1< x2 < 0 ,∴ y1 < y2 ,即 y1 - y2 < 0.
反比例函数
四、归纳总结,提升新知
九 下 数 学 课 堂
回顾本课的学习,回答以下问题?
1. 反比例函数的图象有什么特征?
(1) 当 k > 0 时,双曲线的两支分别位于第一、第三象限,在每一个象限内,y 随 x 的增大而减小;
一般的,反比例函数 的图象是双曲线,
(2) 当 k < 0 时,双曲线的两支分别位于第二、第四象限,在每一个象限内,y 随 x 的增大而增大.
反比例函数
四、归纳总结,提升新知
九 下 数 学 课 堂
回顾本课的学习,回答以下问题?
2. 反比例函数有哪些性质?
3. 我们是如何研究反比例函数的图象与性质的?
(1) 当 k > 0 时,在 x < 0 或 x > 0 时,y 随 x 的增大而减小;
(2) 当 k < 0 时,在 x < 0 或 x > 0 时,y 随 x 的增大而增大.
描点绘图,观察图象、猜想结论、验证规律,注意数形结合解决问题;
探究函数的图象性质:图象的形状,图象所在位置,图象的变化趋势,以及函数的增减性等.
反比例函数
五、课后作业
教材 P8 页,习题 26.1 的第 3 题;
教材 P9 页,习题 26.1 的第 5 题、第 8 题.
九 下 数 学 课 堂
九 下 数 学 课 堂
反比例函数
谢 谢 观 看 !
