1.9带电粒子在电场中的运动(共31张ppt)
文档属性
| 名称 | 1.9带电粒子在电场中的运动(共31张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 913.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-02-27 16:27:27 | ||
图片预览








文档简介
(共31张PPT)
带电粒子在电场中的运动
复习提问
1牛顿第二定律的表达式是什么?
2动能定理的表达式?
3.电场力做功的计算公式?
4.匀变速直线运动的基本公式有哪些?
速度公式
位移公式
导出公式
V=v0+at
x=v0t+1/2at2
v2-vo2=2ax
5.平抛运动的相关知识点。
G
3、某些带电体是否考虑重力,要根据题目暗示或运动状态来判定
电场中的带电粒子一般可分为两类:
1、带电的基本粒子:如电子e,质子11H,α粒子,正负离子等。这些粒子所受重力和电场力相比在小得多,除非有说明或明确的暗示以外,一般都不考虑重力。(但并不能忽略质量)。
2、带电微粒:如带电小球、液滴、尘埃等。除非有说明或明确的暗示以外,一般都考虑重力。
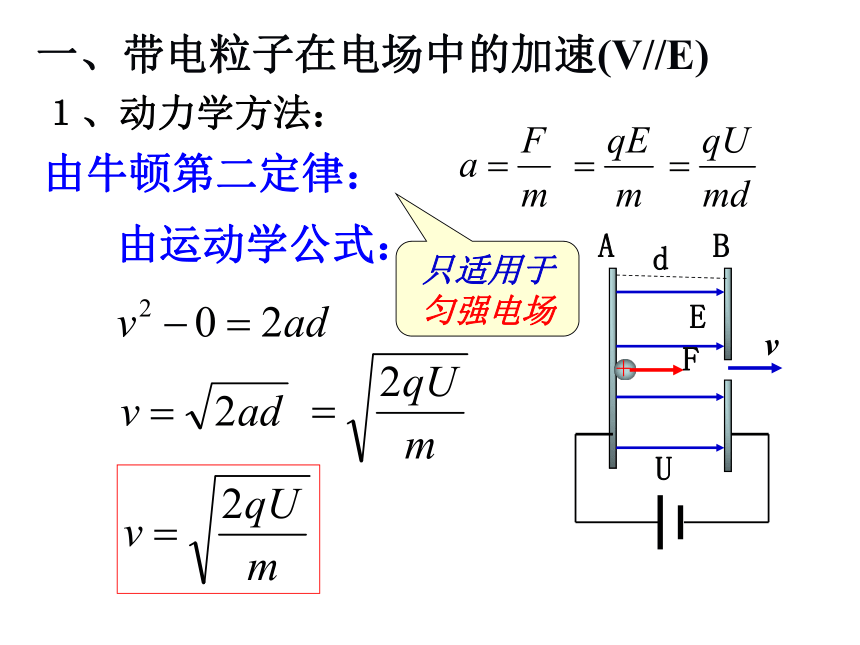
1、动力学方法:
一、带电粒子在电场中的加速(V//E)
A
B
U
d
E
+
F
v
由牛顿第二定律:
由运动学公式:
只适用于匀强电场
2、动能定理:
A
B
U
d
E
+
v
由动能定理:
也适用于非匀强电场
一、带电粒子在电场中的加速
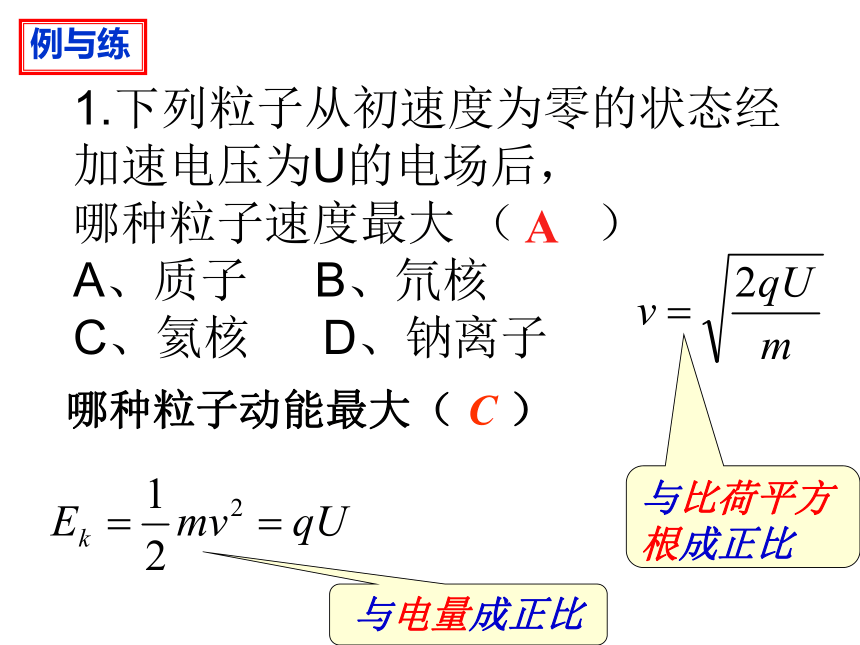
1.下列粒子从初速度为零的状态经加速电压为U的电场后,
哪种粒子速度最大
(
)
A、质子
B、氘核
C、氦核
D、钠离子
A
哪种粒子动能最大(
)
C
例与练
与电量成正比
与比荷平方根成正比
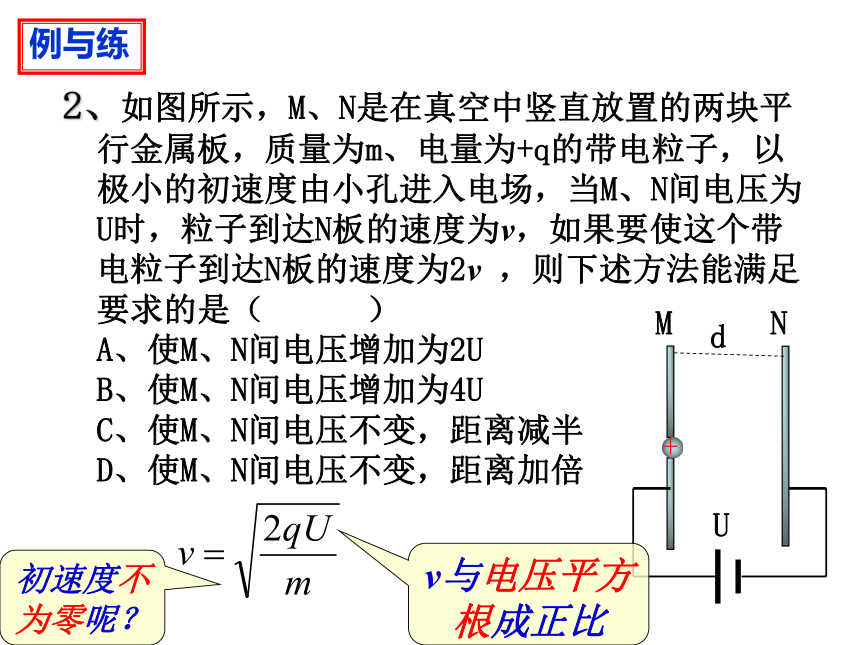
2、如图所示,M、N是在真空中竖直放置的两块平行金属板,质量为m、电量为+q的带电粒子,以极小的初速度由小孔进入电场,当M、N间电压为U时,粒子到达N板的速度为v,如果要使这个带电粒子到达N板的速度为2v
,则下述方法能满足要求的是(
)
A、使M、N间电压增加为2U
B、使M、N间电压增加为4U
C、使M、N间电压不变,距离减半
D、使M、N间电压不变,距离加倍
例与练
M
N
U
d
+
v与电压平方根成正比
初速度不为零呢?
3、如图所示的电场中有A、B两点,A、B的电势差UAB=100V,一个质量为m=2.0×10-12kg、电量为q=-5.0×10-8C的带电粒子,以初速度v0
=3.0×103m/s由A点运动到B点,求粒子到达B点时的速率。(不计粒子重力)
例与练
A
-
v0
B
q为负
解:带电粒子在非匀强电场中只受电场力由动能定理得:
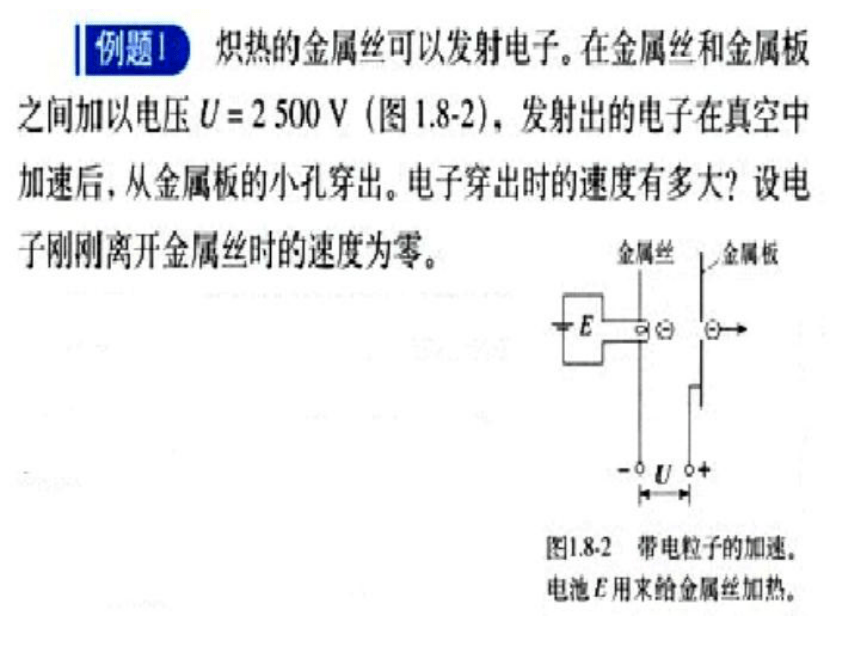
例题2:如图所示,水平放置的A、B两平行板相距h,上板A带正电。现有质量为m,带电量为+q的小球在B板下方距离为H处,以初速度V0竖直向上从B板小孔进入板间电场,欲使小球刚好打到A板,A、B间电势差UAB应为多少?
解:将动能定理用于运动全过程,由W合=△Ek得
-mg(H+h)-qUAB=0-
mV2
0
1
2
整理可得
UAB=
m〔V2-2g(H+h)〕
2q
h
A
B
V0
H
+
+++++++++++++
-
-
-
-
-
-
-
-
-
-
-
-
-
带电粒子
在电场中的运动
(第二课时)
课前小测
一初速度为零的带电粒子经电压为U0=4.0×103V匀强电场加速后获得v=5.0×103m/s的速度,粒子通过
加速电场的时间t=1.0×10-4s,不计
重力作用,则:
(1)带电粒子的荷质比(q/m)为多大?
(2)匀强电场的场强为多大?
(3)粒子通过电场过程中的位移为多大?
v
二、带电粒子在匀强电场中的偏转(V0⊥E)
l
d
+
-
-
-
-
-
-
-
-
-
-
-
+
+
+
+
+
+
+
+
+
+
+
U
v0
q、m
F
平抛运动水平方向和竖直方向个做什么运动呢?
二、带电粒子在匀强电场中的偏转
l
d
+
-
-
-
-
-
-
-
-
-
-
-
+
+
+
+
+
+
+
+
+
+
+
U
v0
q、m
F
+
v
v0
vy
y
θ
偏转角
侧移
1.沿初速度V0方向:做匀速直线运动:
2.垂直V0方向:做初速度为零的匀加速直线运动:
Vy=at
Y=
at2
1
2
类平抛运动
Vx=V0
X=V0t
二、带电粒子在匀强电场中的偏转
类平抛运动
与粒子比荷q/m成正比
与粒子初速度v0平方成反比
与电场的属性U、l、d有关
二、带电粒子在匀强电场中的偏转
与粒子比荷q/m成正比
与粒子初速度v0平方成反比
与电场的属性U、l、d有关
类平抛运动
4、质量为m、带电量为q的粒子以初速度v从中线垂直进入偏转电场,刚好离开电场,它在离开电场后偏转角正切为0.5,则下列说法中正确的是(
)
A、如果偏转电场的电压为原来的一半,则粒子离开电场后的偏转角正切为0.25
B、如果带电粒子的比荷为原来的一半,则粒子离开电场后的偏转角正切为0.25
C、如果带电粒子的初速度为原来的2倍,则粒子离开电场后的偏转角正切为0.25
D、如果带电粒子的初动能为原来的2倍,则粒子离开电场后的偏转角正切为0.25
例与练
偏转角正切与比荷成正比
偏转角正切与初动能成反比
偏转角正切与电压成正比
5、质子(质量为m、电量为e)和二价氦离子(质量为4m、电量为2e)以相同的初动能垂直射入同一偏转电场中,离开电场后,它们的偏转角正切之比为
,侧移之比为
。
例与练
与电量成正比
与电量成正比
6、三个电子在同一地点沿同一直线垂直飞入偏转电场,如图所示。则由此可判断(
)
A、
b和c同时飞离电场
B、在b飞离电场的瞬间,a刚好打在下极板上
C、进入电场时,c速度最大,a速度最小
D、c的动能增量最小,
a和b的动能增量一样大
例与练
析与解
7、如图,电子在电势差为U1的加速电场中由静止开始加速,然后射入电势差为U2的两块平行极板间的电场中,入射方向跟极板平行。整个装置处在真空中,重力可忽略。在满足电子能射出平行板区的条件下,下述四种情况中,一定能使电子的偏转角θ变大的是
(
)
A、U1变大、U2变大
B、U1变小、U2变大
C、U1变大、U2变小
D、U1变小、U2变小
例与练
析与解
对加速过程由动能定理:
对偏转过程由偏转角正切公式:
与粒子的电量q、质量m无关
8、如图所示,二价氦离子和质子的混合体,经同一加速电场加速后,垂直射入同一偏转电场中,偏转后,打在同一荧光屏上,则它们(
)
A、侧移相同
B、偏转角相同
C、到达屏上同一点
D、到达屏上不同点
例与练
与粒子的电量q、质量m无关
9、试证明:带电粒子垂直进入偏转电场,离开电场时就好象是从初速度所在直线的中点沿直线离开电场的。
例与练
θ
x
10、如图所示,有一电子(电量为e、质量为m)经电压U0加速后,沿平行金属板A、B中心线进入两板,A、B板间距为d、长度为L,
A、B板间电压为U,屏CD足够大,距离A、B板右边缘2L,AB板的中心线过屏CD的中心且与屏CD垂直。试求电子束打在屏上的位置到屏中心间的距离。
例与练
析与解
电子离开电场,就好象从中点沿直线离开的:
θ
对加速过程由动能定理:
11、质量为1×10-25kg、电量为1×10-16C的带电粒子以2×106m/s速度从水平放置的平行金属板A、B中央沿水平方向飞入板间,如图所示。已知板长L=10cm,间距d=2cm,当AB间电压在
范围内时,此带电粒子能从板间飞出。
例与练
v0
+
+
+
+
+
-
-
-
-
-
v0
+
+
+
+
+
-
-
-
-
-
θ
析与解
对偏转过程由偏转角正切公式:
或对偏转过程由侧移公式:
带电粒子在电场中的运动
复习提问
1牛顿第二定律的表达式是什么?
2动能定理的表达式?
3.电场力做功的计算公式?
4.匀变速直线运动的基本公式有哪些?
速度公式
位移公式
导出公式
V=v0+at
x=v0t+1/2at2
v2-vo2=2ax
5.平抛运动的相关知识点。
G
3、某些带电体是否考虑重力,要根据题目暗示或运动状态来判定
电场中的带电粒子一般可分为两类:
1、带电的基本粒子:如电子e,质子11H,α粒子,正负离子等。这些粒子所受重力和电场力相比在小得多,除非有说明或明确的暗示以外,一般都不考虑重力。(但并不能忽略质量)。
2、带电微粒:如带电小球、液滴、尘埃等。除非有说明或明确的暗示以外,一般都考虑重力。
1、动力学方法:
一、带电粒子在电场中的加速(V//E)
A
B
U
d
E
+
F
v
由牛顿第二定律:
由运动学公式:
只适用于匀强电场
2、动能定理:
A
B
U
d
E
+
v
由动能定理:
也适用于非匀强电场
一、带电粒子在电场中的加速
1.下列粒子从初速度为零的状态经加速电压为U的电场后,
哪种粒子速度最大
(
)
A、质子
B、氘核
C、氦核
D、钠离子
A
哪种粒子动能最大(
)
C
例与练
与电量成正比
与比荷平方根成正比
2、如图所示,M、N是在真空中竖直放置的两块平行金属板,质量为m、电量为+q的带电粒子,以极小的初速度由小孔进入电场,当M、N间电压为U时,粒子到达N板的速度为v,如果要使这个带电粒子到达N板的速度为2v
,则下述方法能满足要求的是(
)
A、使M、N间电压增加为2U
B、使M、N间电压增加为4U
C、使M、N间电压不变,距离减半
D、使M、N间电压不变,距离加倍
例与练
M
N
U
d
+
v与电压平方根成正比
初速度不为零呢?
3、如图所示的电场中有A、B两点,A、B的电势差UAB=100V,一个质量为m=2.0×10-12kg、电量为q=-5.0×10-8C的带电粒子,以初速度v0
=3.0×103m/s由A点运动到B点,求粒子到达B点时的速率。(不计粒子重力)
例与练
A
-
v0
B
q为负
解:带电粒子在非匀强电场中只受电场力由动能定理得:
例题2:如图所示,水平放置的A、B两平行板相距h,上板A带正电。现有质量为m,带电量为+q的小球在B板下方距离为H处,以初速度V0竖直向上从B板小孔进入板间电场,欲使小球刚好打到A板,A、B间电势差UAB应为多少?
解:将动能定理用于运动全过程,由W合=△Ek得
-mg(H+h)-qUAB=0-
mV2
0
1
2
整理可得
UAB=
m〔V2-2g(H+h)〕
2q
h
A
B
V0
H
+
+++++++++++++
-
-
-
-
-
-
-
-
-
-
-
-
-
带电粒子
在电场中的运动
(第二课时)
课前小测
一初速度为零的带电粒子经电压为U0=4.0×103V匀强电场加速后获得v=5.0×103m/s的速度,粒子通过
加速电场的时间t=1.0×10-4s,不计
重力作用,则:
(1)带电粒子的荷质比(q/m)为多大?
(2)匀强电场的场强为多大?
(3)粒子通过电场过程中的位移为多大?
v
二、带电粒子在匀强电场中的偏转(V0⊥E)
l
d
+
-
-
-
-
-
-
-
-
-
-
-
+
+
+
+
+
+
+
+
+
+
+
U
v0
q、m
F
平抛运动水平方向和竖直方向个做什么运动呢?
二、带电粒子在匀强电场中的偏转
l
d
+
-
-
-
-
-
-
-
-
-
-
-
+
+
+
+
+
+
+
+
+
+
+
U
v0
q、m
F
+
v
v0
vy
y
θ
偏转角
侧移
1.沿初速度V0方向:做匀速直线运动:
2.垂直V0方向:做初速度为零的匀加速直线运动:
Vy=at
Y=
at2
1
2
类平抛运动
Vx=V0
X=V0t
二、带电粒子在匀强电场中的偏转
类平抛运动
与粒子比荷q/m成正比
与粒子初速度v0平方成反比
与电场的属性U、l、d有关
二、带电粒子在匀强电场中的偏转
与粒子比荷q/m成正比
与粒子初速度v0平方成反比
与电场的属性U、l、d有关
类平抛运动
4、质量为m、带电量为q的粒子以初速度v从中线垂直进入偏转电场,刚好离开电场,它在离开电场后偏转角正切为0.5,则下列说法中正确的是(
)
A、如果偏转电场的电压为原来的一半,则粒子离开电场后的偏转角正切为0.25
B、如果带电粒子的比荷为原来的一半,则粒子离开电场后的偏转角正切为0.25
C、如果带电粒子的初速度为原来的2倍,则粒子离开电场后的偏转角正切为0.25
D、如果带电粒子的初动能为原来的2倍,则粒子离开电场后的偏转角正切为0.25
例与练
偏转角正切与比荷成正比
偏转角正切与初动能成反比
偏转角正切与电压成正比
5、质子(质量为m、电量为e)和二价氦离子(质量为4m、电量为2e)以相同的初动能垂直射入同一偏转电场中,离开电场后,它们的偏转角正切之比为
,侧移之比为
。
例与练
与电量成正比
与电量成正比
6、三个电子在同一地点沿同一直线垂直飞入偏转电场,如图所示。则由此可判断(
)
A、
b和c同时飞离电场
B、在b飞离电场的瞬间,a刚好打在下极板上
C、进入电场时,c速度最大,a速度最小
D、c的动能增量最小,
a和b的动能增量一样大
例与练
析与解
7、如图,电子在电势差为U1的加速电场中由静止开始加速,然后射入电势差为U2的两块平行极板间的电场中,入射方向跟极板平行。整个装置处在真空中,重力可忽略。在满足电子能射出平行板区的条件下,下述四种情况中,一定能使电子的偏转角θ变大的是
(
)
A、U1变大、U2变大
B、U1变小、U2变大
C、U1变大、U2变小
D、U1变小、U2变小
例与练
析与解
对加速过程由动能定理:
对偏转过程由偏转角正切公式:
与粒子的电量q、质量m无关
8、如图所示,二价氦离子和质子的混合体,经同一加速电场加速后,垂直射入同一偏转电场中,偏转后,打在同一荧光屏上,则它们(
)
A、侧移相同
B、偏转角相同
C、到达屏上同一点
D、到达屏上不同点
例与练
与粒子的电量q、质量m无关
9、试证明:带电粒子垂直进入偏转电场,离开电场时就好象是从初速度所在直线的中点沿直线离开电场的。
例与练
θ
x
10、如图所示,有一电子(电量为e、质量为m)经电压U0加速后,沿平行金属板A、B中心线进入两板,A、B板间距为d、长度为L,
A、B板间电压为U,屏CD足够大,距离A、B板右边缘2L,AB板的中心线过屏CD的中心且与屏CD垂直。试求电子束打在屏上的位置到屏中心间的距离。
例与练
析与解
电子离开电场,就好象从中点沿直线离开的:
θ
对加速过程由动能定理:
11、质量为1×10-25kg、电量为1×10-16C的带电粒子以2×106m/s速度从水平放置的平行金属板A、B中央沿水平方向飞入板间,如图所示。已知板长L=10cm,间距d=2cm,当AB间电压在
范围内时,此带电粒子能从板间飞出。
例与练
v0
+
+
+
+
+
-
-
-
-
-
v0
+
+
+
+
+
-
-
-
-
-
θ
析与解
对偏转过程由偏转角正切公式:
或对偏转过程由侧移公式:
