_2020-2021学年苏科版七年级下册7.4.1 三角形的概念、分类、三边关系课件(24z2ppt )
文档属性
| 名称 | _2020-2021学年苏科版七年级下册7.4.1 三角形的概念、分类、三边关系课件(24z2ppt ) |

|
|
| 格式 | pptx | ||
| 文件大小 | 167.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-28 00:00:00 | ||
图片预览


文档简介
7.4.1 三角形的概念、分类、三边关系
学习目标:
1.掌握三角形的概念(已经学过);
2.三角形的表示方法;
2.三角形的分类(已经学过);
3.三角形的性质(重难点);
重难点:
三角形的三边关系在题目中的应用;
一.三角形的定义:
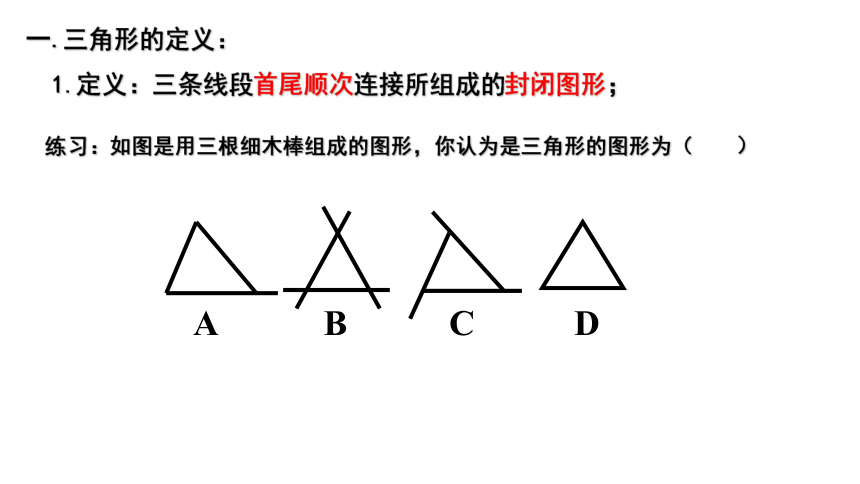
1.定义:三条线段首尾顺次连接所组成的封闭图形;
练习:如图是用三根细木棒组成的图形,你认为是三角形的图形为( )
D
A
B
C
一.三角形的定义:
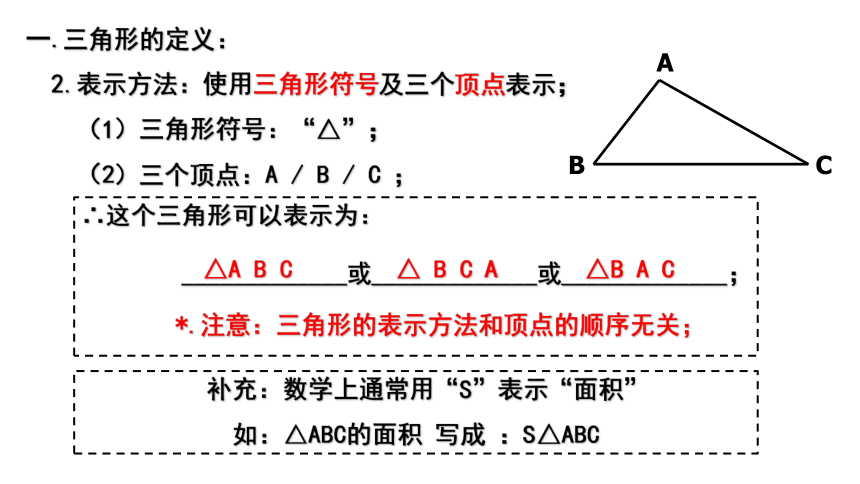
2.表示方法:使用三角形符号及三个顶点表示;
(1)三角形符号:“△”;
(2)三个顶点:A / B / C ;
A
B
C
∴这个三角形可以表示为:
_____________或_____________或_____________;
△A B C
△B A C
△ B C A
*.注意:三角形的表示方法和顶点的顺序无关;
补充:数学上通常用“S”表示“面积”
如:△ABC的面积 写成 :S△ABC
练习:
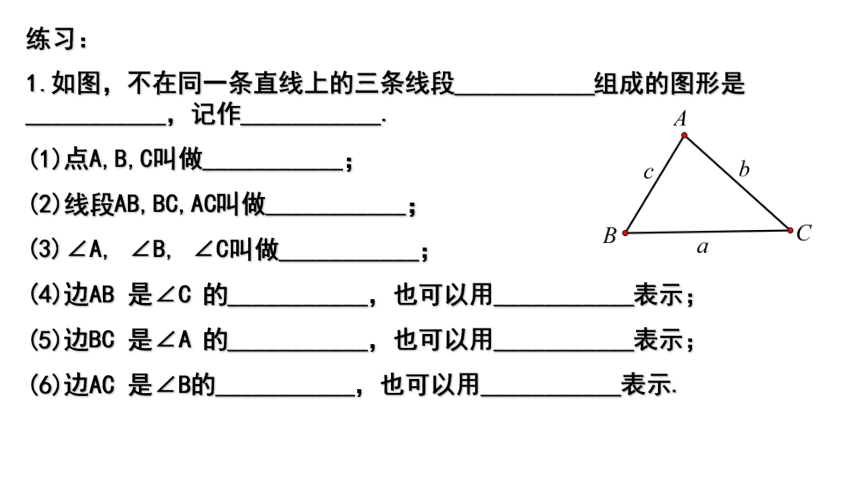
1.如图,不在同一条直线上的三条线段___________组成的图形是___________,记作___________.
(1)点A,B,C叫做___________;
(2)线段AB,BC,AC叫做___________;
(3)∠A, ∠B, ∠C叫做___________;
(4)边AB 是∠C 的___________,也可以用___________表示;
(5)边BC 是∠A 的___________,也可以用___________表示;
(6)边AC 是∠B的___________,也可以用___________表示.
二.三角形的分类:
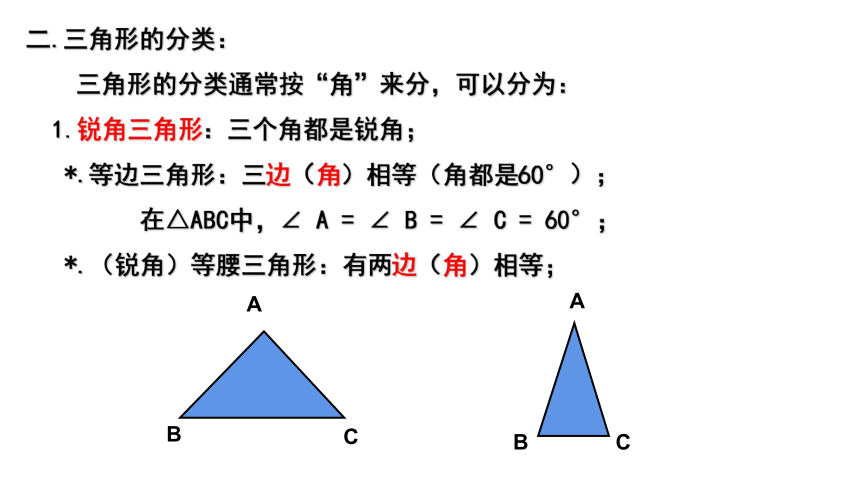
三角形的分类通常按“角”来分,可以分为:
1.锐角三角形:三个角都是锐角;
*.等边三角形:三边(角)相等(角都是60°);
在△ABC中,∠ A = ∠ B = ∠ C = 60°;
*.(锐角)等腰三角形:有两边(角)相等;
A
C
B
A
C
B
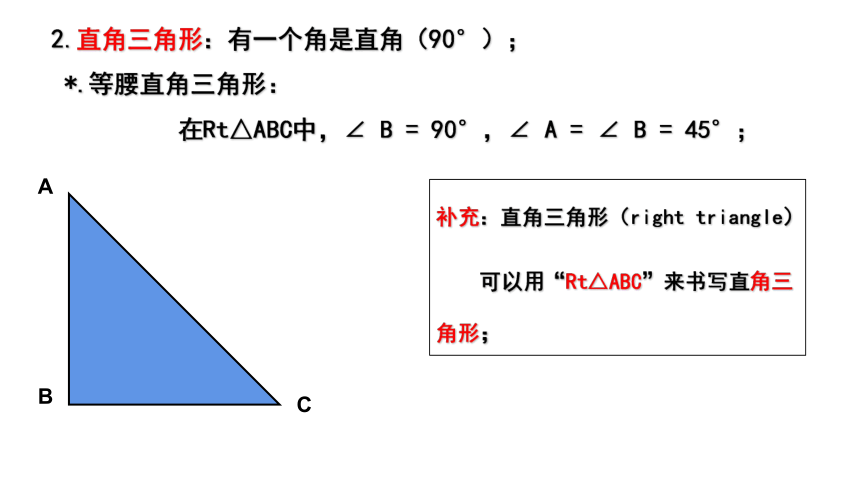
2.直角三角形:有一个角是直角(90°);
*.等腰直角三角形:
在Rt△ABC中,∠ B = 90°,∠ A = ∠ B = 45°;
A
B
C
补充:直角三角形(right triangle)
可以用“Rt△ABC”来书写直角三角形;
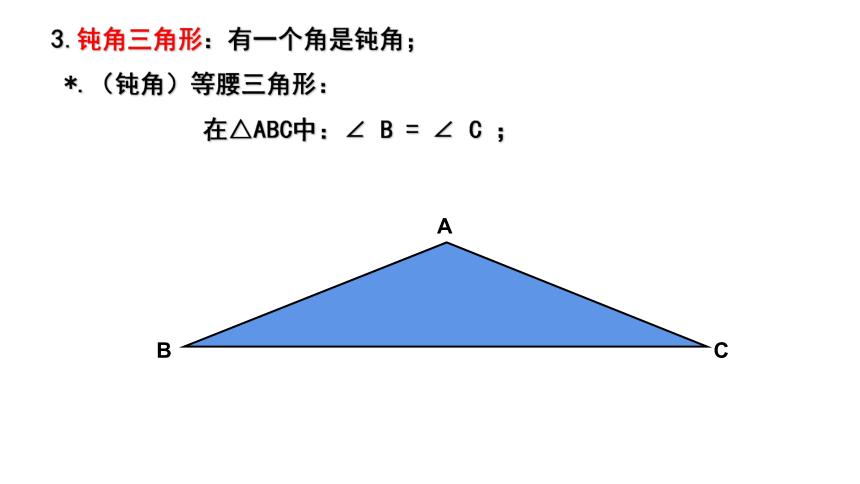
3.钝角三角形:有一个角是钝角;
*.(钝角)等腰三角形:
在△ABC中:∠ B = ∠ C ;
A
B
C
练习:
1.如图,思考下列问题:
(1)△ABD的边是________________;
(2)△ABD的角是_____________________;
(3)∠B的对边是_______________________;
(4)以AD为边的三角形是____________________________;
(5)写出2个直角三角形是____________________________;
(6)以AD为边的钝角三角形是____________________________.
练习:
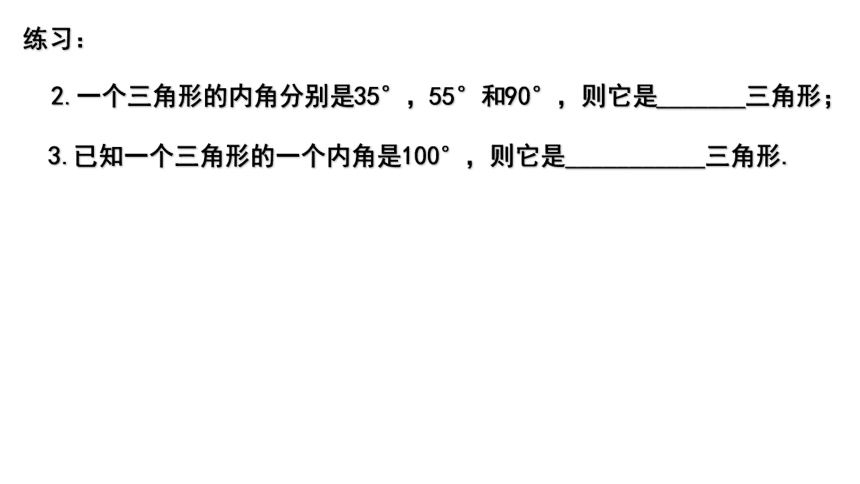
2.一个三角形的内角分别是35°,55°和90°,则它是_______三角形;
3.已知一个三角形的一个内角是100°,则它是___________三角形.
三.三角形的性质(重点):
*.预备知识:
1.内角:三角形内部的角;
*.在△ABC中:∠A ;∠B; ∠C是内角;
2.外角:三角形内角的邻补角;
3.角的对边:三角形中每一个角都对应着一条边;
*.在△ABC中:
∠A 的对边是_____; ∠B 的对边是_____; ∠C 的对边是_____;
A
B
C
b
a
c
c
b
a
三.三角形的性质(重点):
(一)关于“角”的性质(下一节课学习):
1.三角形的内角和是180°;
即:∠ A + ∠ B + ∠ C =180°
2.三角形的外角和360°;
A
B
C
b
a
c
A
B
C
*.思考:如果用“两点之间线段最短”说面三角形三边关系?
(二)关于“边”的性质(难点):
1.三角形的两边之和大于第三边
a+b>c a+c>b b+c>a
a-b<c a-c<b b-c<a
A
B
C
c-b<a b-a<c a-c<b
移项
2.三角形的两边之差小于第三边
c
a
b
*.若不满足以上条件即,构不成三角形!
练习:
1.有两根长度分别为4cm和7cm的木棒搭三角形,
(1)第三边的范围是:________________________________.
(2)如果第三边长是奇数,那么第三边可能是_______________;
(3)如果周长是奇数,那么第三边可能是________________________.
练习:
2.等腰三角形两边长分别为3和5,则这个三角形的周长为__________;
3.等腰三角形两边长分别为5和11,则这个三角形的周长为_________.
4.下列长度的三条线段,能组成三角形的是( )
A.2,2,5 B.2,4,5 C.3,3,6 D.4,2,1
5.等腰三角形两边长分别为4和9,则这个三角形的周长为________;
6.等腰三角形的周长为16,其中一边长为4,则其腰长为________;
练习:
7.下列说法:
①三角形按边分类可分为三边不等的三角形、等腰三角形和等边三角形;
②等边三角形是特殊的等腰三角形;
③等腰三角形是特殊的等边三角形;
④有两边相等的三角形一定是等腰三角形;
其中,说法正确的是__________________;
(三)三角形的“高线”:
从三角形的一个顶点向它的对边作垂线,顶点与垂足之间的线段叫“高线”,也就是我们平时所说的“高”;
A
B
C
b
a
c
*.注意:
∵a边上的高是:_________;
∴________⊥________;
∵b边上的高是:_________;
∴________⊥________;
∵c边上的高是:_________;
∴________⊥________;
M
Q
N
线段AN
线段BM
线段CQ
AN
BC
BM
CM
CQ
BQ
锐角三角形 直角三角形 钝角三角形
一定在内部
一定在顶点
一定在外部
*.结论:(1)锐角三角形的三条高的延长线的交点一定在内部;
(2)直角三角形的三条高的延长线的交点一定在顶点;
(3)钝角三角形的三条高的延长线的交点一定在外部;
练习:
1.下列四个图形中,线段BE是△ABC的高的是?
练习:
3.如图,在△ABC中,∠ACB=90°,CD⊥AD,垂足为点D,下列说法:
①点A与点B的距离是线段AB的长;
②点A到直线CD的距离是线段AD的长;
③线段CD是△ABC边AB上的高;
④线段CD是△BCD边BD上的高.
正确的_____________________;
(四)三角形的“角平分线”:
一个内角的平分线与这个角的对边相交,这个角的顶点与交点的线段(简化:三角形内角的角平分线段);
A
B
C
b
a
c
*.注意:
∵∠A的角平分线是:_________;
∴________=________;
∵∠B的角平分线是:_________;
∴________=________;
∵∠C的角平分线是:_________;
∴________=________;
M
Q
N
*.结论:
三角形的三条角平分线的延长线的交点一定在三角形内部;
线段AN
∠BAN
线段BM
线段CQ
∠CAN
∠ABM
∠CBM
∠ACQ
∠BCQ
(五)三角形的“中线”:
连接一个顶点与它对边中点的线段;
A
B
C
b
a
c
*.注意:
∵a的中线是:_________;
∴________=________;
∵b的中线是:_________;
∴________=________;
∵c的中线是:_________;
∴________=________;
M
Q
N
*.结论:
三角形的三条角中线的延长线的交点一定在三角形内部;
线段AN
线段BM
线段CQ
BN CN
CM AM
AQ BQ
练习:
1.若线段AM、AN分别是△ABC中BC边上的高线和中线,则( )
A.AM>AN B.AM>AN或AM=AN
C.AM<AN D.AM<AN或AM=AN
2.如图,AE是△ABC的中线,已知EC=4,DE=2,则BD的长为( )
A.2 B.3 C.4 D.6
练习:
3.如图,已知AD是△ABC的边BC上的中线,CE是△ADC的边AD上的中线,若△ABD的面积为16cm2,则△CDE的面积为( )
A.32 cm2 B.16cm2 C.8cm2 D.4cm2
三.三角形的性质:
总结:
1.三角形的中线、高线、角平分线一定都是_________;
2.任意的一个三角形都具有:
_____条中线,_____条高线,_____条角平分线;
3.三角形的中线、角平分线一定在三角形______,但高线不一定;
4.“中线”平分边,“角平分线”平分角,“高线”垂直边;
线段
3 3 3
内部
学习目标:
1.掌握三角形的概念(已经学过);
2.三角形的表示方法;
2.三角形的分类(已经学过);
3.三角形的性质(重难点);
重难点:
三角形的三边关系在题目中的应用;
一.三角形的定义:
1.定义:三条线段首尾顺次连接所组成的封闭图形;
练习:如图是用三根细木棒组成的图形,你认为是三角形的图形为( )
D
A
B
C
一.三角形的定义:
2.表示方法:使用三角形符号及三个顶点表示;
(1)三角形符号:“△”;
(2)三个顶点:A / B / C ;
A
B
C
∴这个三角形可以表示为:
_____________或_____________或_____________;
△A B C
△B A C
△ B C A
*.注意:三角形的表示方法和顶点的顺序无关;
补充:数学上通常用“S”表示“面积”
如:△ABC的面积 写成 :S△ABC
练习:
1.如图,不在同一条直线上的三条线段___________组成的图形是___________,记作___________.
(1)点A,B,C叫做___________;
(2)线段AB,BC,AC叫做___________;
(3)∠A, ∠B, ∠C叫做___________;
(4)边AB 是∠C 的___________,也可以用___________表示;
(5)边BC 是∠A 的___________,也可以用___________表示;
(6)边AC 是∠B的___________,也可以用___________表示.
二.三角形的分类:
三角形的分类通常按“角”来分,可以分为:
1.锐角三角形:三个角都是锐角;
*.等边三角形:三边(角)相等(角都是60°);
在△ABC中,∠ A = ∠ B = ∠ C = 60°;
*.(锐角)等腰三角形:有两边(角)相等;
A
C
B
A
C
B
2.直角三角形:有一个角是直角(90°);
*.等腰直角三角形:
在Rt△ABC中,∠ B = 90°,∠ A = ∠ B = 45°;
A
B
C
补充:直角三角形(right triangle)
可以用“Rt△ABC”来书写直角三角形;
3.钝角三角形:有一个角是钝角;
*.(钝角)等腰三角形:
在△ABC中:∠ B = ∠ C ;
A
B
C
练习:
1.如图,思考下列问题:
(1)△ABD的边是________________;
(2)△ABD的角是_____________________;
(3)∠B的对边是_______________________;
(4)以AD为边的三角形是____________________________;
(5)写出2个直角三角形是____________________________;
(6)以AD为边的钝角三角形是____________________________.
练习:
2.一个三角形的内角分别是35°,55°和90°,则它是_______三角形;
3.已知一个三角形的一个内角是100°,则它是___________三角形.
三.三角形的性质(重点):
*.预备知识:
1.内角:三角形内部的角;
*.在△ABC中:∠A ;∠B; ∠C是内角;
2.外角:三角形内角的邻补角;
3.角的对边:三角形中每一个角都对应着一条边;
*.在△ABC中:
∠A 的对边是_____; ∠B 的对边是_____; ∠C 的对边是_____;
A
B
C
b
a
c
c
b
a
三.三角形的性质(重点):
(一)关于“角”的性质(下一节课学习):
1.三角形的内角和是180°;
即:∠ A + ∠ B + ∠ C =180°
2.三角形的外角和360°;
A
B
C
b
a
c
A
B
C
*.思考:如果用“两点之间线段最短”说面三角形三边关系?
(二)关于“边”的性质(难点):
1.三角形的两边之和大于第三边
a+b>c a+c>b b+c>a
a-b<c a-c<b b-c<a
A
B
C
c-b<a b-a<c a-c<b
移项
2.三角形的两边之差小于第三边
c
a
b
*.若不满足以上条件即,构不成三角形!
练习:
1.有两根长度分别为4cm和7cm的木棒搭三角形,
(1)第三边的范围是:________________________________.
(2)如果第三边长是奇数,那么第三边可能是_______________;
(3)如果周长是奇数,那么第三边可能是________________________.
练习:
2.等腰三角形两边长分别为3和5,则这个三角形的周长为__________;
3.等腰三角形两边长分别为5和11,则这个三角形的周长为_________.
4.下列长度的三条线段,能组成三角形的是( )
A.2,2,5 B.2,4,5 C.3,3,6 D.4,2,1
5.等腰三角形两边长分别为4和9,则这个三角形的周长为________;
6.等腰三角形的周长为16,其中一边长为4,则其腰长为________;
练习:
7.下列说法:
①三角形按边分类可分为三边不等的三角形、等腰三角形和等边三角形;
②等边三角形是特殊的等腰三角形;
③等腰三角形是特殊的等边三角形;
④有两边相等的三角形一定是等腰三角形;
其中,说法正确的是__________________;
(三)三角形的“高线”:
从三角形的一个顶点向它的对边作垂线,顶点与垂足之间的线段叫“高线”,也就是我们平时所说的“高”;
A
B
C
b
a
c
*.注意:
∵a边上的高是:_________;
∴________⊥________;
∵b边上的高是:_________;
∴________⊥________;
∵c边上的高是:_________;
∴________⊥________;
M
Q
N
线段AN
线段BM
线段CQ
AN
BC
BM
CM
CQ
BQ
锐角三角形 直角三角形 钝角三角形
一定在内部
一定在顶点
一定在外部
*.结论:(1)锐角三角形的三条高的延长线的交点一定在内部;
(2)直角三角形的三条高的延长线的交点一定在顶点;
(3)钝角三角形的三条高的延长线的交点一定在外部;
练习:
1.下列四个图形中,线段BE是△ABC的高的是?
练习:
3.如图,在△ABC中,∠ACB=90°,CD⊥AD,垂足为点D,下列说法:
①点A与点B的距离是线段AB的长;
②点A到直线CD的距离是线段AD的长;
③线段CD是△ABC边AB上的高;
④线段CD是△BCD边BD上的高.
正确的_____________________;
(四)三角形的“角平分线”:
一个内角的平分线与这个角的对边相交,这个角的顶点与交点的线段(简化:三角形内角的角平分线段);
A
B
C
b
a
c
*.注意:
∵∠A的角平分线是:_________;
∴________=________;
∵∠B的角平分线是:_________;
∴________=________;
∵∠C的角平分线是:_________;
∴________=________;
M
Q
N
*.结论:
三角形的三条角平分线的延长线的交点一定在三角形内部;
线段AN
∠BAN
线段BM
线段CQ
∠CAN
∠ABM
∠CBM
∠ACQ
∠BCQ
(五)三角形的“中线”:
连接一个顶点与它对边中点的线段;
A
B
C
b
a
c
*.注意:
∵a的中线是:_________;
∴________=________;
∵b的中线是:_________;
∴________=________;
∵c的中线是:_________;
∴________=________;
M
Q
N
*.结论:
三角形的三条角中线的延长线的交点一定在三角形内部;
线段AN
线段BM
线段CQ
BN CN
CM AM
AQ BQ
练习:
1.若线段AM、AN分别是△ABC中BC边上的高线和中线,则( )
A.AM>AN B.AM>AN或AM=AN
C.AM<AN D.AM<AN或AM=AN
2.如图,AE是△ABC的中线,已知EC=4,DE=2,则BD的长为( )
A.2 B.3 C.4 D.6
练习:
3.如图,已知AD是△ABC的边BC上的中线,CE是△ADC的边AD上的中线,若△ABD的面积为16cm2,则△CDE的面积为( )
A.32 cm2 B.16cm2 C.8cm2 D.4cm2
三.三角形的性质:
总结:
1.三角形的中线、高线、角平分线一定都是_________;
2.任意的一个三角形都具有:
_____条中线,_____条高线,_____条角平分线;
3.三角形的中线、角平分线一定在三角形______,但高线不一定;
4.“中线”平分边,“角平分线”平分角,“高线”垂直边;
线段
3 3 3
内部
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
