湘教版数学八年级下册1.2.3直角三角形性质和判定二课件(15张PPT)
文档属性
| 名称 | 湘教版数学八年级下册1.2.3直角三角形性质和判定二课件(15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-28 12:38:38 | ||
图片预览






文档简介
1.2.3 直角三角形的性质判定二
勾股定理逆定理
直角三角形两直角边a, b的平方和, 等于斜边c的平方.
在 Rt ?ABC中 a2 + b2 = c2
1、勾股定理的内容:
a
b
c
A
B
C
知识回顾
a
b
c
A
B
C
若已知a、b,则 c=
若已知a、c , 则 b=
若已知b、c,则 a=
2、使用勾股定理求边时常用下面三个式子:
知识回顾
如图1-19,在△ABC 中,AB = c,BC = a,AC = b,
且a2+ b2 =c2 , 那么△ABC是直角三角形吗?
图1-19
如果我们能构造一个直角三角形, 然后证明△ABC 与所构造的直角三角
形全等, 即可得△ABC 是直角三角形.
新知探究
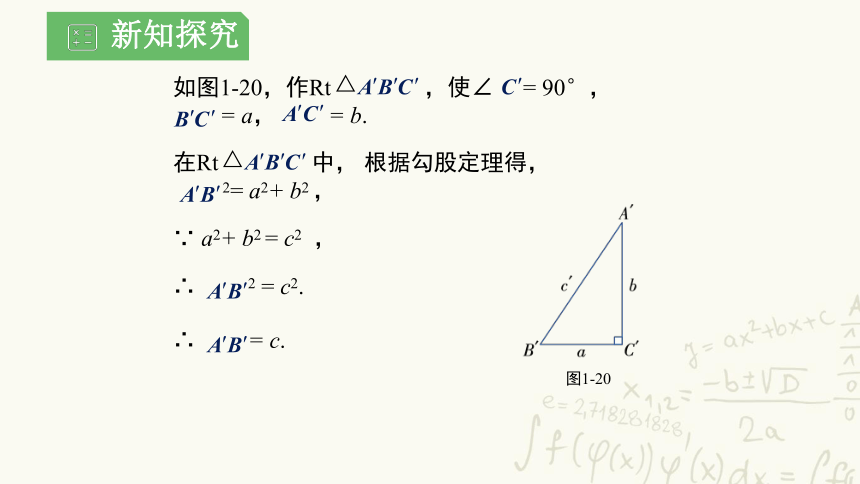
∵ a2+ b2 = c2 ,
图1-20
∴ = c.
如图1-20,作Rt ,使∠ = 90°,
= a, = b.
△
在Rt 中, 根据勾股定理得,
2= a2+ b2 ,
△
∴ 2 = c2.
新知探究
∴ △ABC是直角三角形.
先构造满足某些条件的
图形,然后根据所求证的图
形与所构造图形之间的关系,
完成证明,这也是常用的问
题解决策略.
在△ABC和 中,
∵ BC = = a,AC = = b,
AB = = c,
△
∴ △ABC≌
△
∴ ∠C =∠ = 90°.
新知探究
如果三角形的三条边长a,b,c 满足关系:
,那么这个三角形是直角三角形.
由此得到直角三角形的判定定理:
上述定理被称为勾股定理的逆定理.
新知探究
分析 根据勾股定理的逆定理, 判断一个三角形是不是直角三角形, 只要看两条较短边长的平方和是否等于最长边的平方.
例
判断由线段a,b,c组成的三角形是不是直角三角形.
(1)a = 6,b = 8,c = 10;
(2)a = 12,b = 15,c = 20.
找最长边
例题讲解
满足a2+ b2 = c2的
三个正整数称为勾股
数.
(2) ∵ 122 + 152 = 369, 202 = 400,
∴ 122 + 152≠202.
∴ 这个三角形不是直角三角形.
(1) ∵ 62 + 82 = 100, 102 = 100,
∴ 62 + 82 = 100.
∴这个三角形是直角三角形.
解
(1)a = 6,b = 8,c = 10;
(2)a = 12,b = 15,c = 20.
例题讲解
常见勾股数.
3.4.5
7.24.25
5.12.13
9.40.41
6.8.10
新知探究
解:(1)∵12+( )2=1+3=4, 22=4,
∴ 12+( )2=22.
∴这个三角形是直角三角形.
(1)a=1,b=2,c= ; (2)a:b:c=3:4:5.
判断由a、b、c组成的三角形是不是直角三角形:
(2)设a=3x, b=4x, c=5x,则
∵(3x)2+(4x )2=25x2, (5x)2= 25x2,
∴ (3x)2+(4x )2 = (5x)2.
∴这个三角形是直角三角形
随堂练习
例
如图1-21,在△ABC 中,已知AB = 10,BD = 6, AD = 8,AC = 17. 求DC的长.
在△ABD中,AB = 10,BD = 6,AD = 8,
∵ 62 + 82 = 102 ,
解
即AD2 + BD2 = AB2 ,
∴ △ADB为直角三角形.
∴ ∠ADB = 90°.
∴ ∠ADC = 180°-∠ADB = 90°.
在Rt△ADC中,DC2 = AC2 - AD2 ,
∴
图1-21
例题讲解
(8-x)
x
10
10
A
B
C
D
F
E
8
6
4
x
解:设DE为x,则CE为 (8-x).
CE2+CF2=EF2
(8-x)2+42=x2
x=5
分析:在Rt?AEF中,求AE
矩形ABCD如图折叠,使点D落在BC边上的点F处,已知AB=8,BC=10,求折痕AE的长。
即:EF=5.
在Rt?AEF中,AE= = =5
√
5
√
AF2+EF2
√
102+52
例题讲解
勾股定理的逆定理
如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形.且边C所对的角为直角.
a2 + b2 = c2
课堂总结
16页习题1.2 A组第2题
作业布置
勾股定理逆定理
直角三角形两直角边a, b的平方和, 等于斜边c的平方.
在 Rt ?ABC中 a2 + b2 = c2
1、勾股定理的内容:
a
b
c
A
B
C
知识回顾
a
b
c
A
B
C
若已知a、b,则 c=
若已知a、c , 则 b=
若已知b、c,则 a=
2、使用勾股定理求边时常用下面三个式子:
知识回顾
如图1-19,在△ABC 中,AB = c,BC = a,AC = b,
且a2+ b2 =c2 , 那么△ABC是直角三角形吗?
图1-19
如果我们能构造一个直角三角形, 然后证明△ABC 与所构造的直角三角
形全等, 即可得△ABC 是直角三角形.
新知探究
∵ a2+ b2 = c2 ,
图1-20
∴ = c.
如图1-20,作Rt ,使∠ = 90°,
= a, = b.
△
在Rt 中, 根据勾股定理得,
2= a2+ b2 ,
△
∴ 2 = c2.
新知探究
∴ △ABC是直角三角形.
先构造满足某些条件的
图形,然后根据所求证的图
形与所构造图形之间的关系,
完成证明,这也是常用的问
题解决策略.
在△ABC和 中,
∵ BC = = a,AC = = b,
AB = = c,
△
∴ △ABC≌
△
∴ ∠C =∠ = 90°.
新知探究
如果三角形的三条边长a,b,c 满足关系:
,那么这个三角形是直角三角形.
由此得到直角三角形的判定定理:
上述定理被称为勾股定理的逆定理.
新知探究
分析 根据勾股定理的逆定理, 判断一个三角形是不是直角三角形, 只要看两条较短边长的平方和是否等于最长边的平方.
例
判断由线段a,b,c组成的三角形是不是直角三角形.
(1)a = 6,b = 8,c = 10;
(2)a = 12,b = 15,c = 20.
找最长边
例题讲解
满足a2+ b2 = c2的
三个正整数称为勾股
数.
(2) ∵ 122 + 152 = 369, 202 = 400,
∴ 122 + 152≠202.
∴ 这个三角形不是直角三角形.
(1) ∵ 62 + 82 = 100, 102 = 100,
∴ 62 + 82 = 100.
∴这个三角形是直角三角形.
解
(1)a = 6,b = 8,c = 10;
(2)a = 12,b = 15,c = 20.
例题讲解
常见勾股数.
3.4.5
7.24.25
5.12.13
9.40.41
6.8.10
新知探究
解:(1)∵12+( )2=1+3=4, 22=4,
∴ 12+( )2=22.
∴这个三角形是直角三角形.
(1)a=1,b=2,c= ; (2)a:b:c=3:4:5.
判断由a、b、c组成的三角形是不是直角三角形:
(2)设a=3x, b=4x, c=5x,则
∵(3x)2+(4x )2=25x2, (5x)2= 25x2,
∴ (3x)2+(4x )2 = (5x)2.
∴这个三角形是直角三角形
随堂练习
例
如图1-21,在△ABC 中,已知AB = 10,BD = 6, AD = 8,AC = 17. 求DC的长.
在△ABD中,AB = 10,BD = 6,AD = 8,
∵ 62 + 82 = 102 ,
解
即AD2 + BD2 = AB2 ,
∴ △ADB为直角三角形.
∴ ∠ADB = 90°.
∴ ∠ADC = 180°-∠ADB = 90°.
在Rt△ADC中,DC2 = AC2 - AD2 ,
∴
图1-21
例题讲解
(8-x)
x
10
10
A
B
C
D
F
E
8
6
4
x
解:设DE为x,则CE为 (8-x).
CE2+CF2=EF2
(8-x)2+42=x2
x=5
分析:在Rt?AEF中,求AE
矩形ABCD如图折叠,使点D落在BC边上的点F处,已知AB=8,BC=10,求折痕AE的长。
即:EF=5.
在Rt?AEF中,AE= = =5
√
5
√
AF2+EF2
√
102+52
例题讲解
勾股定理的逆定理
如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形.且边C所对的角为直角.
a2 + b2 = c2
课堂总结
16页习题1.2 A组第2题
作业布置
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
