第2章 图形与变换

2.1图形的平移
1. 在平面内，将线段AB沿某个方向平移距离为a㎝，那么图形上的每个点都沿此方向移动了 ㎝，平移不改变线段的 和 。
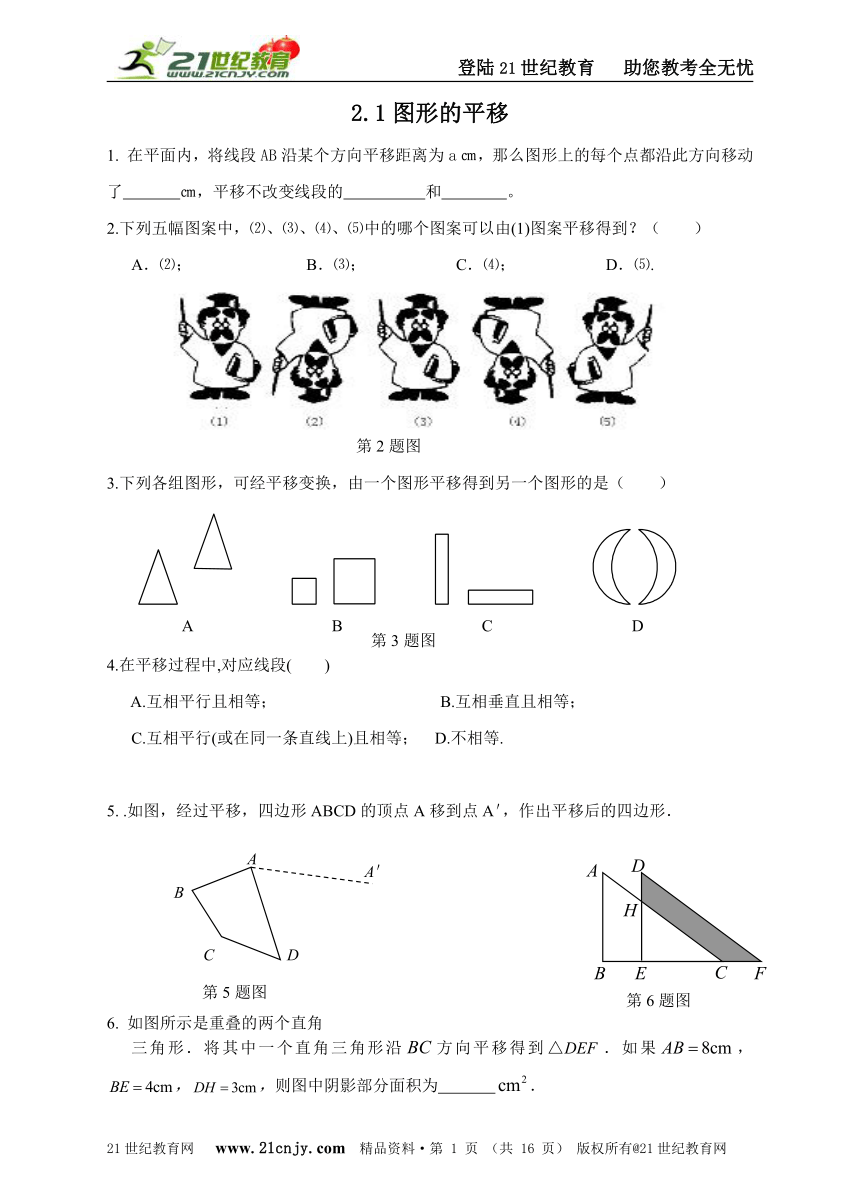
2.下列五幅图案中，⑵、⑶、⑷、⑸中的哪个图案可以由(1)图案平移得到？（ ）
A．⑵； B．⑶； C．⑷； D．⑸.
3.下列各组图形，可经平移变换，由一个图形平移得到另一个图形的是（ ）
4.在平移过程中,对应线段( )
A.互相平行且相等； B.互相垂直且相等；
C.互相平行(或在同一条直线上)且相等； D.不相等.
5. .如图，经过平移，四边形ABCD的顶点A移到点A＇，作出平移后的四边形．
6. 如图所示是重叠的两个直角
三角形．将其中一个直角三角形沿方向平移得到．如果，，，则图中阴影部分面积为 ．
2.2 图形的旋转
1.一条线段绕其上一点旋转90°与原来的线段位置关系是 ．
2．下列大写字母A，B，C，D，E，F，G，H，I，J，K，L，M，N，O，P，Q，R，S，T，U，V，W，X，Y，Z旋转180°和原来形状一样的有 ．
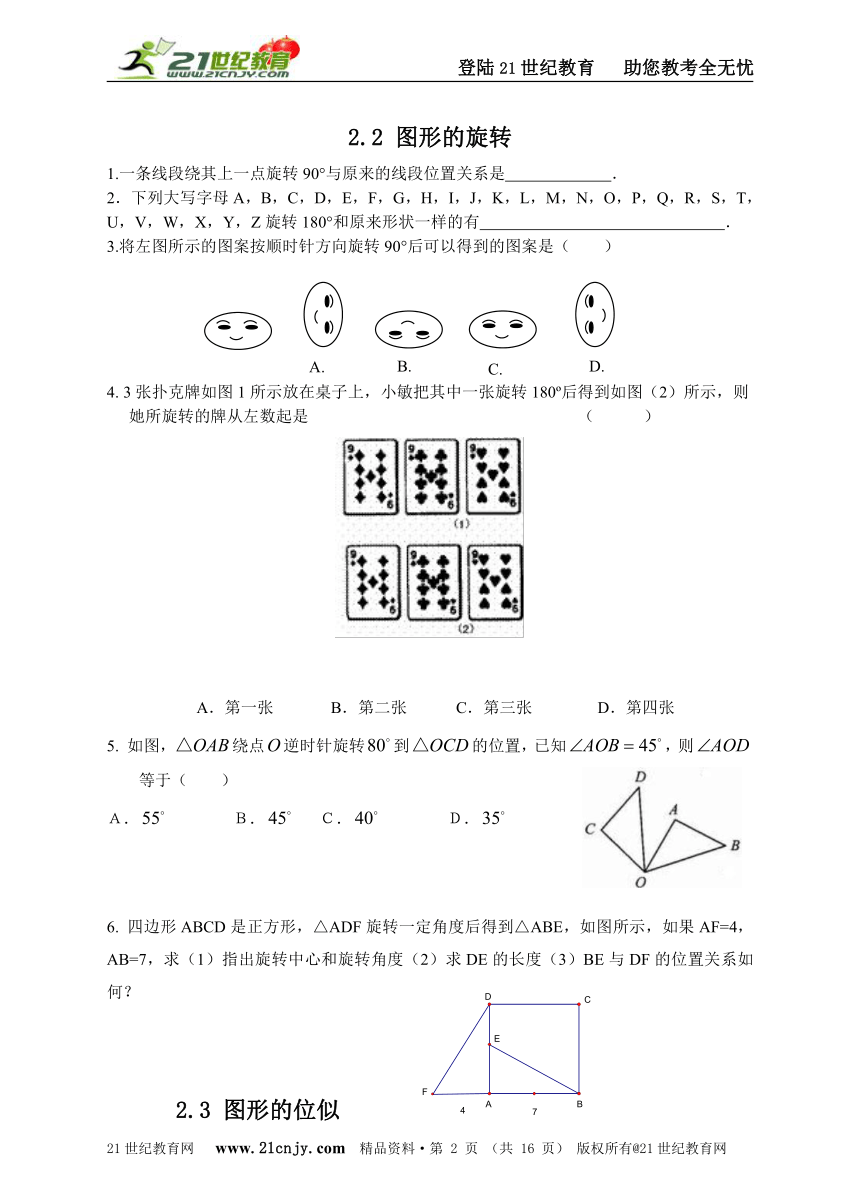
3.将左图所示的图案按顺时针方向旋转90°后可以得到的图案是（ ）
4. 3张扑克牌如图1所示放在桌子上，小敏把其中一张旋转180o后得到如图（2）所示，则她所旋转的牌从左数起是 （ ）
A．第一张 B．第二张 C．第三张 D．第四张
5. 如图，绕点逆时针旋转到的位置，已知，则等于（　　）
Ａ．　 Ｂ．　 Ｃ．　 Ｄ．
6. 四边形ABCD是正方形，△ADF旋转一定角度后得到△ABE，如图所示，如果AF=4，AB=7，求（1）指出旋转中心和旋转角度（2）求DE的长度（3）BE与DF的位置关系如何？
2.3 图形的位似
1. 下列说法不正确的是 （ ）
A．位似图形一定是相似图形
B. 相似图形不一定是位似图形
C. 位似图形上任意一对对应点到位似中心的距离之比等于位似比
D. 位似图形中每组对应点所在的直线必相互平行
2. 把一个正多边形放大到原来的2.5倍，则原图与新图的相似比为________．
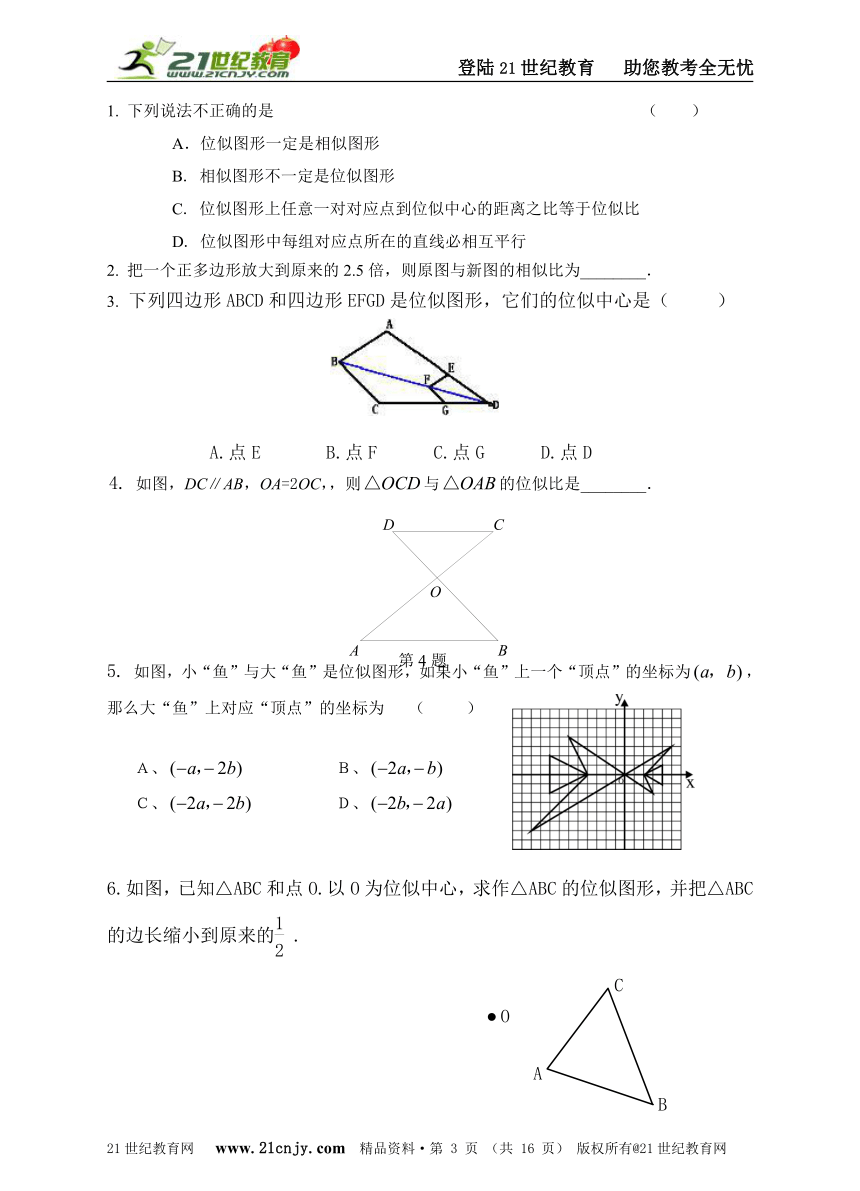
3. 下列四边形ABCD和四边形EFGD是位似图形，它们的位似中心是（ ）

A.点E B.点F C.点G D.点D
4. 如图，DC∥AB，OA=2OC，，则与的位似比是________．
5. 如图，小“鱼”与大“鱼”是位似图形，如果小“鱼”上一个“顶点”的坐标为，那么大“鱼”上对应“顶点”的坐标为 （ ）
Ａ、 Ｂ、
Ｃ、 Ｄ、
6.如图，已知△ABC和点O.以O为位似中心，求作△ABC的位似图形，并把△ABC的边长缩小到原来的.
《图形与变换》
45分钟基础测试+能力测试题
一.选择题(每小题4分,共24分)
1.下面的图形中，是中心对称图形的是 （　 　）

A． B． C． D．
2. 下面给出的是一些产品的商标图案，从几何图形的角度看(不考虑文字和字母)，既是轴对称图形又能旋转180°后与原图重合的是( )

3. 将一圆形纸片对折后再对折，得到图4，然后沿着图中的虚线剪开，
得到两部分，其中一部分展开后的平面图形是 ( )
?
4. 下列说法中正确的是 （ ）
角平分线上任意一点到角的两边的线段长相等
角是轴对称图形 ③线段不是轴对称图形
线段垂直平分线上的点到这条线段两个端点的距离相等
A.①②③④ B.①②③ C.②④ D.②③④
5. 如图，有一矩形纸片ABCD，AB=6，AD=8，将纸片折叠，使AB
落在AD边上，折痕为AE，再将△AEB以BE为折痕向右折叠，AE与DC交于点F，则的值是（ ）A．1 B． C． D．
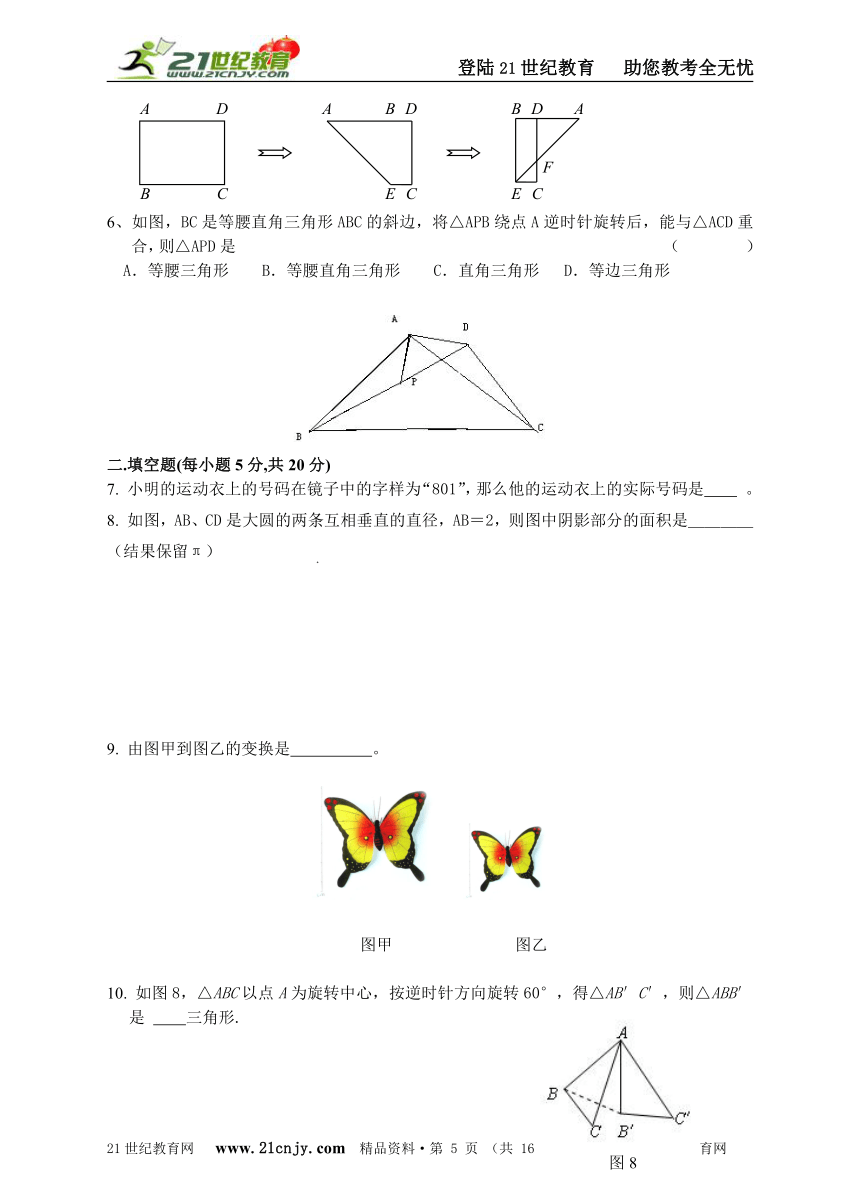
6、如图，BC是等腰直角三角形ABC的斜边，将△APB绕点A逆时针旋转后，能与△ACD重合，则△APD是 （ ）
A．等腰三角形 B．等腰直角三角形 C．直角三角形 D．等边三角形
二.填空题(每小题5分,共20分)
7. 小明的运动衣上的号码在镜子中的字样为“801”，那么他的运动衣上的实际号码是 。
8. 如图，AB、CD是大圆的两条互相垂直的直径，AB＝2，则图中阴影部分的面积是＿＿＿＿（结果保留π）
9. 由图甲到图乙的变换是 。

图甲 图乙
10. 如图8，△ABC以点A为旋转中心，按逆时针方向旋转60°，得△AB′C′，则△ABB′是 三角形.
三.解答题(共56分)
11. 如图12，四边形ABCD的∠BAD=∠C=90o,AB=AD,AE⊥BC于E,旋转后能与重合。（12分）
(1）旋转中心是哪一点?
(2）旋转了多少度?
(3）如果点A是旋转中心，那么点B经过旋转后，点B旋转到什么位置？
12. 如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，
连接DE，F为线段DE上一点，且∠AFE＝∠B.
求证：（1）△ADF∽△DEC（10分）
（2）若AB＝4,AD＝3,AE＝3,求AF的长.（10分）
13. 用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合，使三角尺的60°角的顶点与点A重合，两边分别与AB、AC重合.将三角尺绕点A按逆时针方向旋转.
（1）当三角尺的两边分别与菱形的两边BC、CD相交于点E、F时（如图所示），通过观察或测量BE、CF的长度，你能得出什么结论？并证明你的结论；（12分）
（2）当三角尺的两边分别与菱形的两边BC、CD的延长线相交于点E、F时（如图所示），你在（1）中得到的结论还成立吗？说明理由。（12分）
能力测试(选做题)
1. 如图4，C是线段BD上一点，分别以BC、CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F，BE交AC于G，则图中可通过旋转而相互得到的三角形对数有( )．
A．1对 B．2对 C．3对 D．4对
2. 如图3的方格纸中，左边图形到右边图形的变换是（　　）
A．向右平移7格
B．以AB的垂直平分线为对称轴作轴对称，再以AB为对称轴作轴对称
C．绕AB的中点旋转1800，再以AB为对称轴作轴对称
D．以AB为对称轴作轴对称，再向右平移7格
3. 如图，已知图中的每个小方格
都是边长为1的小正方形，每个小正方形的顶点称为格
点.若△ABC与△是位似图形，且顶点都在格点
上，则位似中心的坐标是 ．
4. 如图，在△ABC中，D是BC边上一点，E是AC边上一点，且满足AD=AB，∠ADE=∠C.（1）求证：∠AED=∠ADC，∠DEC=∠B；
（2）求证：AB2=AE·AC
九年级数学第一学期第二章测试题
时限：90分钟 分值：120分
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
一.选择题(每小题3分,共36分)
1.在以下现象中，① 温度计中，液柱的上升或下降；　　② 打气筒打气时，活塞的运动；③ 钟摆的摆动；　　④ 传送带上，瓶装饮料的移动：属于平移的是（　　 ）．　
A． ②④　 B．　①③　　 C．　②③ D．　①②　　
２．下列图形中，是由(1)仅通过平移得到的是(　　)
　　　　
3. 如图可以看作是一个等腰直角三角形旋转若干次而生成的则
每次旋转的度数可以是（　　）
A．900 B．600 C．450 D．300
4、如图，△ABC与△A＇B＇C＇关于点O成中心对称，则下列结论不成立的是（ ）
A、点A与点A＇是对称点　　　B、 BO=B＇O
C、AB∥A＇B＇ D、∠ACB= ∠C＇A＇B＇
5. 下列说法正确的是（ ）
平移不改变图形的形状和大小，而旋转则改变图形的形状和大小
平移和旋转的共同点是改变图形的位置
C、 图形可以向某方向平移一定距离，也可以向某方向旋转一定距离
D、 在平移和旋转图形中，对应角相等，对应线段相等且平行

6. 将 图形按顺时针方向旋转900后的图形是( )
A B C D
7. 下列说法正确的是 （ ）
A. 分别在△ABC的边AB，AC的反向延长线上取点D，E，使DE∥BC,则△ADE是△ABC放大后的图形
B. 两位似图形的面积之比等于位似比
C. 位似多边形中对应对角线之比等于位似比
D. 位似图形的周长之比等于位似比的平方
8. 如图，点分别是各边的中点，下列说法中，错误的是（ ）
A. 平分 B. C. 与互相平分 D.△DEF是△ABC的位似图形
9. 用作位似图形的方法，可以将一个图形放大或缩小，位似中心 （ ）
A. 只能选在原图形的外部 B. 只能选在原图形的内部
C. 只能选在原图形的边上 D．可以选择任意位置
10.如图已知BC∥DE，则下列说法中不正确的是 （ ）
A．两个三角形是位似图形 B．点A是两个三角形的位似中心
C．AE︰Ac是位似比 D．点B与点E、点C与点D是对应位似点
11. 如图，以A为位似中心，将△ADE放大2倍后，得位似图形△ABC，若 表示△ADE的面积，表示四边形DBCE的面积，则= （ ）
A． 1︰2 B．1︰3 C．1︰4 D．2︰3
12. 如图，在正方形ABCD中，E为DC边上的点，连结BE，将△BCE绕点C顺时针方向旋转900得到△DCF，连结EF，若∠BEC=600，则∠EFD的度数为（ ）A、100 B、150 C、200 D、250
第12题图
二.填空题(每小题3分,共15分)
13. 平移不改变图形的 和 　，只改变图形的 。
14.△ABC和△DCE是等边三角形，则在此图中，△ACE绕着c点 旋转 度可得到△BCD.
（第14题图） （第15题图）
15. 如图，将三角尺ABC（其中∠ABC＝60°，∠C＝90°）绕B点按顺时针方向转动一个角度到A1BC1的位置，使得点A，B，C1在同一条直线上，那么这个角度等于 。
16已知△ABC，以点A为位似中心，作出△ADE，使△ADE是△ABC放大2倍的图形，这样的图形可以作出 个。 .
17. 如图，所示是重叠的两个直角三角形．将其中一个直角三角形沿方向平移得到．如果，，，则图中阴影部分面积为 ．
三.解答题(共69分)
18. 平移方格纸中的图形，使A点平移到A′点处，画出平移后的图形，并写上一句贴切、诙谐的解说词．

19. 经过平移,作出平移后的三角形.
20. 如图所示，已知正方形ABCD中的△DCF可以经过旋转得到△ECB。
（1）图中哪一个点是旋转中心？
（2）按什么方向旋转了多少度？
（3）如果CF=3cm，求EF的长。
21.试一试：某个学生为学校设计了一个直角三角形的绿化带，有一块是正方形草坪和两块直角三角形的花坛组成，现在只知道两个直角三角形的两条斜边长分别为3米和6米，你能求出花坛的面积是多少吗？
22. ．如图，方格纸中的每个小方格都是边长为1的正方形，我们把以格点间连线为边的三角形称为“格点三角形”，图中的是格点三角形．在建立平面直角坐标系后，点的坐标为（）．
（1）把向左平移8格后得到，画出的图形并写出点的坐标；
（2）把绕点按顺时针方向旋转后得到，画出的图形并写出点的坐标；
（3）把以点为位似中心放大，使放大前后对应边长的比为，画出的图形．
2.1图形的平移
参考答案
1、a 大小 形状 2、B 3、A 4、C
5、图形略 6、26
2.2 图形的旋转
参考答案
垂直 2、H I N O S X Z
3、A 4、A 5、D
6、旋转中心：点A 旋转角度：90°
DE=3 垂直关系
2.3 图形的位似
参考答案
1、D 2、2：5 3、D 4、1：2 5、C
6、画图略
《图形与变换》
45分钟基础测试+能力测试题（参考答案）
1、D
2、C
3、C
4、C
5、C
6、B
7、108
8、０.５Π
9、相似
10、等边
11、（1）点A, （2）90o，（3）点D
12、（1）证明：∵四边形ABCD是平行四边形
∴AD∥BC AB∥CD
∴∠ADF=∠CED ∠B+∠C=180°
∵∠AFE+∠AFD=180 ∠AFE=∠B
∴∠AFD=∠C
∴△ADF∽△DEC
(2)解：∵四边形ABCD是平行四边形
∴AD∥BC CD=AB=4
又∵AE⊥BC ∴ AE⊥AD
在Rt△ADE中，DE=
∵△ADF∽△DEC
∴ ∴ AF=
13、（１）ＢＥ＝ＣＦ，证明⊿ＡＢＥ≌⊿ＡＣＦ可得。
　　　　（２）、结论仍然成立，证明同（１）。
能力测试(选做题)
C
D
(9,0)
4、证明：（1）在△ADE和△ACD中
∵∠ADE=∠C，∠DAE=∠DAE
∴∠AED=180°—∠DAE—∠ADE
∠ADC=180°—∠ADE—∠C
∴∠AED=∠ADC
∵∠AED+∠DEC=180°
∠ADB+∠ADC=180°
∴∠DEC=∠ADB
又∵AB=AD
∴∠ADB=∠B
∴∠DEC=∠B
（2）在△ADE和△ACD中
由（1）知∠ADE=∠C，∠DAE=∠DAE
∴△ADE∽△ACD
∴
即AD2=AE·AC
又AB=AD
∴AB2=AE·AC
九年级数学第一学期第二章测试题
参考答案
1、A 2、C 3、C 4、D 5、B 6、D 7、D 8、A 9、D 10、D
11、C 12、B
13、形状 大小 位置
14、逆时针 60
15、120°
16、2个
17、26
18、画图略，解说词可酌情加分
19、画图略
20、（1）点C
（2）按逆时针方向旋转90度
（3）EF=
21、9平方米
22、（1）画图略，点的坐标为（）；
（2）画图略，点的坐标为（）；
（3）画图略．