五年级数学下册教案-第三单元 长方体和正方体的体积-- 用排水法求不规则物体的体积-人教版
文档属性
| 名称 | 五年级数学下册教案-第三单元 长方体和正方体的体积-- 用排水法求不规则物体的体积-人教版 | 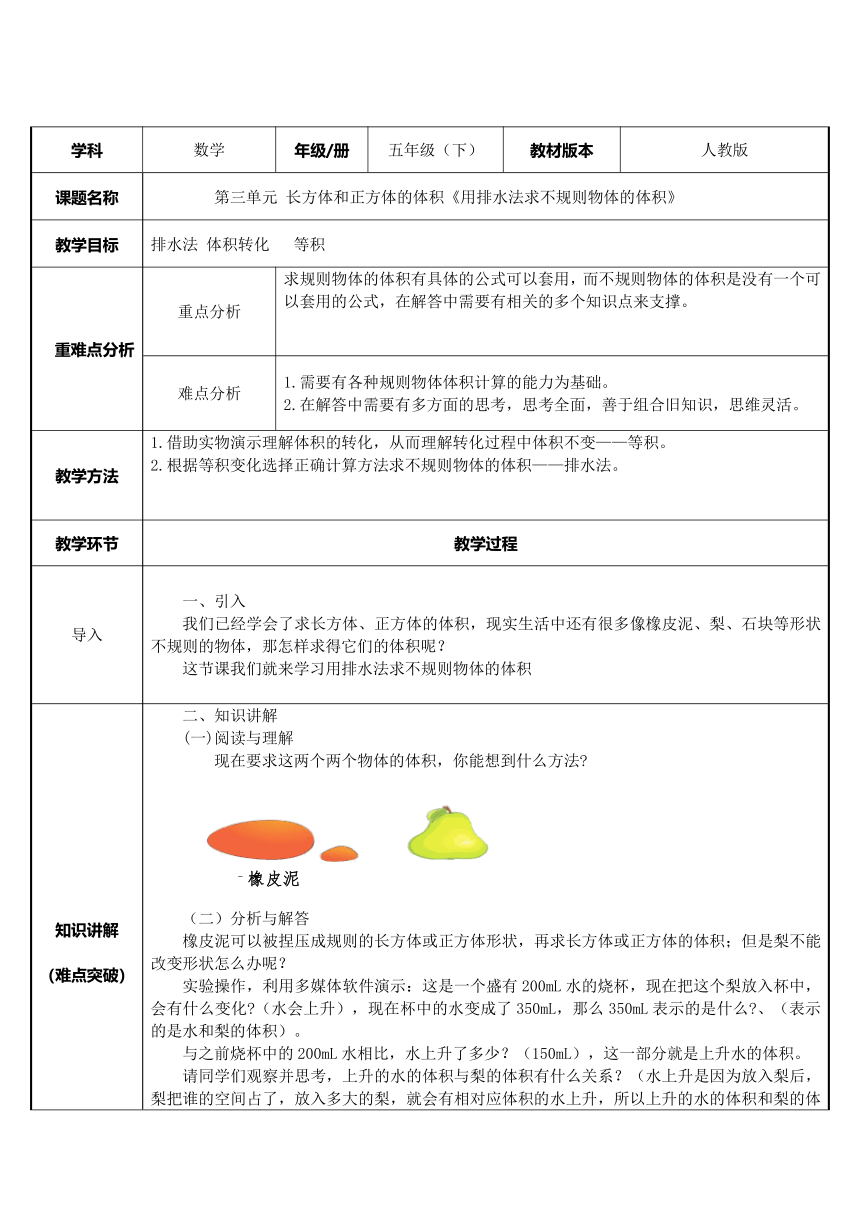 | |
| 格式 | zip | ||
| 文件大小 | 558.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-28 21:06:28 | ||
图片预览

文档简介
学科
数学
年级/册
五年级(下)
教材版本
人教版
课题名称
第三单元
长方体和正方体的体积《用排水法求不规则物体的体积》
教学目标
排水法
体积转化
等积
重难点分析
重点分析
求规则物体的体积有具体的公式可以套用,而不规则物体的体积是没有一个可以套用的公式,在解答中需要有相关的多个知识点来支撑。
难点分析
1.需要有各种规则物体体积计算的能力为基础。2.在解答中需要有多方面的思考,思考全面,善于组合旧知识,思维灵活。
教学方法
1.借助实物演示理解体积的转化,从而理解转化过程中体积不变——等积。2.根据等积变化选择正确计算方法求不规则物体的体积——排水法。
教学环节
教学过程
导入
一、引入我们已经学会了求长方体、正方体的体积,现实生活中还有很多像橡皮泥、梨、石块等形状不规则的物体,那怎样求得它们的体积呢?这节课我们就来学习用排水法求不规则物体的体积
知识讲解(难点突破)
知识讲解(一)阅读与理解
现在要求这两个两个物体的体积,你能想到什么方法?分析与解答橡皮泥可以被捏压成规则的长方体或正方体形状,再求长方体或正方体的体积;但是梨不能改变形状怎么办呢?实验操作,利用多媒体软件演示:这是一个盛有200mL水的烧杯,现在把这个梨放入杯中,会有什么变化?(水会上升),现在杯中的水变成了350mL,那么350mL表示的是什么?、(表示的是水和梨的体积)。与之前烧杯中的200mL水相比,水上升了多少?(150mL),这一部分就是上升水的体积。请同学们观察并思考,上升的水的体积与梨的体积有什么关系?(水上升是因为放入梨后,梨把谁的空间占了,放入多大的梨,就会有相对应体积的水上升,所以上升的水的体积和梨的体积相等)通过实验演示发现:上升的水的体积就是梨的体积,可以列式为350-200=150mL,也就是用水和梨的总体积减去原来水的体积,就是梨的体积。思考:如果容器没有体积刻度,换成是长方体容器,不规则物体的体积该如何算呢?这时我们就要量出(已知)容器的长、宽、原来水的高,以及放入不规则物体后,水的高度。变式拓展例:珊瑚石的体积是多少?方法一:
8×8×7-8×8×6=8×8×(7-6)=64(cm3)方法二:8×8×(7-6)=8×8×1=64(cm3)答:珊瑚石的体积是64cm3。通过刚才的学习,我们发现求不规则物体的体积计算方法有两种:1.水和不规则物体的总体积-原来水的体积=不规则物体的体积2.容器的长×容器的长宽×上升水的高度=不规则物体的体积两种方法,哪一种计算更简便呢?我们来试一试。
课堂练习(难点巩固)
一个长方体玻璃缸,从里面量长40厘米,宽2.5分米,缸内水深12厘米。把一块石头放进缸里,水面升到16厘米,求石头的体积。2.5dm=25cm方法一:
方法二:40×25×16-40×25×12
40×25×(16-12)=40×25×(16-12)
=1000×4=1000×4
=4000(cm3)=4000(cm3)答:石头的体积是4000cm3。两种方法,我认为方法二计算简便,在平时的解答中,两种方法都可以,你可以选择自己喜欢的方法进行解答。想一想:可以利用上面的方法测量乒乓球、冰块的体积吗?为什么?答:不能,因为兵乓球没有沉入水中,而冰块又与水融合在一起了。
小结
四、小结板书设计通过以上内容的学习,我们掌握了如何用排水法求不规则物体的体积,方法有两种:1.水和不规则物体的总体积-原来水的体积=不规则物体的体积;2.容器的长×容器的宽×上升的水的高度=不规则物体的体积。今后在遇到此类题,可以根据题意,选择一种自己喜欢的方法,找出已知条件,正确解答。
橡皮泥
橡皮泥
8cm
8cm
6cm
8cm
8cm
7cm
用排水法求不规则物体的体积
例题:珊瑚石的体积是多少?
8cm
8cm
6cm
8cm
8cm
7cm
8×8×7-8×8×6
=8×8×(7-6)
=64(cm3)
8×8×(7-6)
=8×8×1
=64(cm3)
答:珊瑚石的体积是64cm3。
1.水和不规则物体的总体积-原来水的体积=不规则物体的体积
2.容器的长×容器的宽×上升水的高度=不规则物体的体积
数学
年级/册
五年级(下)
教材版本
人教版
课题名称
第三单元
长方体和正方体的体积《用排水法求不规则物体的体积》
教学目标
排水法
体积转化
等积
重难点分析
重点分析
求规则物体的体积有具体的公式可以套用,而不规则物体的体积是没有一个可以套用的公式,在解答中需要有相关的多个知识点来支撑。
难点分析
1.需要有各种规则物体体积计算的能力为基础。2.在解答中需要有多方面的思考,思考全面,善于组合旧知识,思维灵活。
教学方法
1.借助实物演示理解体积的转化,从而理解转化过程中体积不变——等积。2.根据等积变化选择正确计算方法求不规则物体的体积——排水法。
教学环节
教学过程
导入
一、引入我们已经学会了求长方体、正方体的体积,现实生活中还有很多像橡皮泥、梨、石块等形状不规则的物体,那怎样求得它们的体积呢?这节课我们就来学习用排水法求不规则物体的体积
知识讲解(难点突破)
知识讲解(一)阅读与理解
现在要求这两个两个物体的体积,你能想到什么方法?分析与解答橡皮泥可以被捏压成规则的长方体或正方体形状,再求长方体或正方体的体积;但是梨不能改变形状怎么办呢?实验操作,利用多媒体软件演示:这是一个盛有200mL水的烧杯,现在把这个梨放入杯中,会有什么变化?(水会上升),现在杯中的水变成了350mL,那么350mL表示的是什么?、(表示的是水和梨的体积)。与之前烧杯中的200mL水相比,水上升了多少?(150mL),这一部分就是上升水的体积。请同学们观察并思考,上升的水的体积与梨的体积有什么关系?(水上升是因为放入梨后,梨把谁的空间占了,放入多大的梨,就会有相对应体积的水上升,所以上升的水的体积和梨的体积相等)通过实验演示发现:上升的水的体积就是梨的体积,可以列式为350-200=150mL,也就是用水和梨的总体积减去原来水的体积,就是梨的体积。思考:如果容器没有体积刻度,换成是长方体容器,不规则物体的体积该如何算呢?这时我们就要量出(已知)容器的长、宽、原来水的高,以及放入不规则物体后,水的高度。变式拓展例:珊瑚石的体积是多少?方法一:
8×8×7-8×8×6=8×8×(7-6)=64(cm3)方法二:8×8×(7-6)=8×8×1=64(cm3)答:珊瑚石的体积是64cm3。通过刚才的学习,我们发现求不规则物体的体积计算方法有两种:1.水和不规则物体的总体积-原来水的体积=不规则物体的体积2.容器的长×容器的长宽×上升水的高度=不规则物体的体积两种方法,哪一种计算更简便呢?我们来试一试。
课堂练习(难点巩固)
一个长方体玻璃缸,从里面量长40厘米,宽2.5分米,缸内水深12厘米。把一块石头放进缸里,水面升到16厘米,求石头的体积。2.5dm=25cm方法一:
方法二:40×25×16-40×25×12
40×25×(16-12)=40×25×(16-12)
=1000×4=1000×4
=4000(cm3)=4000(cm3)答:石头的体积是4000cm3。两种方法,我认为方法二计算简便,在平时的解答中,两种方法都可以,你可以选择自己喜欢的方法进行解答。想一想:可以利用上面的方法测量乒乓球、冰块的体积吗?为什么?答:不能,因为兵乓球没有沉入水中,而冰块又与水融合在一起了。
小结
四、小结板书设计通过以上内容的学习,我们掌握了如何用排水法求不规则物体的体积,方法有两种:1.水和不规则物体的总体积-原来水的体积=不规则物体的体积;2.容器的长×容器的宽×上升的水的高度=不规则物体的体积。今后在遇到此类题,可以根据题意,选择一种自己喜欢的方法,找出已知条件,正确解答。
橡皮泥
橡皮泥
8cm
8cm
6cm
8cm
8cm
7cm
用排水法求不规则物体的体积
例题:珊瑚石的体积是多少?
8cm
8cm
6cm
8cm
8cm
7cm
8×8×7-8×8×6
=8×8×(7-6)
=64(cm3)
8×8×(7-6)
=8×8×1
=64(cm3)
答:珊瑚石的体积是64cm3。
1.水和不规则物体的总体积-原来水的体积=不规则物体的体积
2.容器的长×容器的宽×上升水的高度=不规则物体的体积
