2020-2021学年北师大版八年级数学下册1.3.1 线段的垂直平分线 课件(16张ppt)
文档属性
| 名称 | 2020-2021学年北师大版八年级数学下册1.3.1 线段的垂直平分线 课件(16张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 365.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-28 22:25:28 | ||
图片预览






文档简介
你知道为什么吗?
问题引入
第一章 三角形的证明
1.3.1 线段的垂直平分线
八年级数学
主备人:
议课组:第2议课组
议课时间:. 2月 28日
授课时间:第二周 3月10日
学习目标(1分钟)
1.会证明线段垂直平分线的性质定理和判定定理.
2.会用线段垂直平分线的性质定理和判定定理解决问题
自学教材P22“想一想”之前的内容,完成下面问题:
自学指导1(1分钟)
学生自学,教师巡视(6分钟)
2、你能证明线段垂直平分线定理吗?你能用数学符号语言表达出来吗?
1、线段垂直平分线性质定理:
线段垂直平分线上的 到
的距离相等.
点
这条线段两个端点
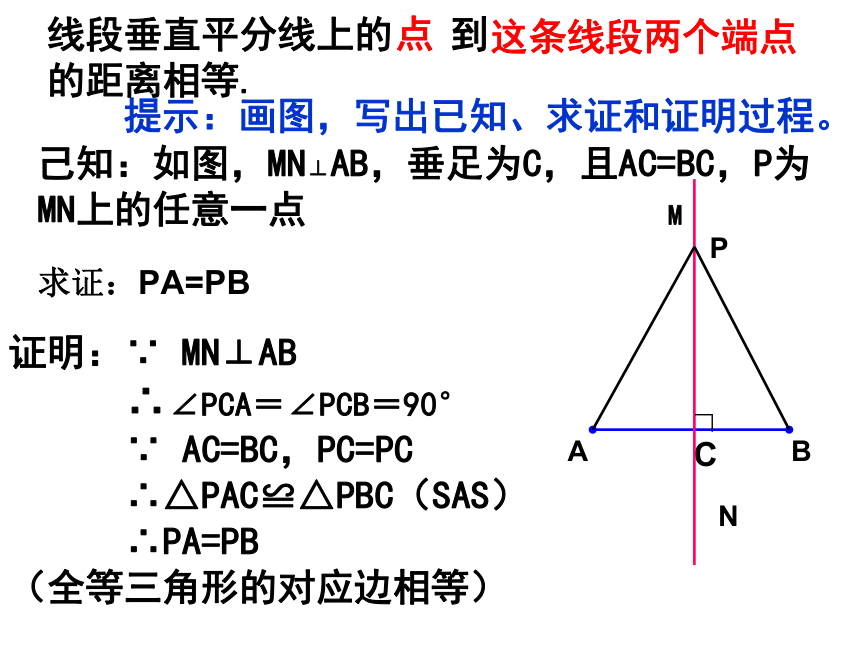
提示:画图,写出已知、求证和证明过程。
证明:∵ MN⊥AB
∴∠PCA=∠PCB=90°
∵ AC=BC,PC=PC
∴△PAC≌△PBC(SAS)
∴PA=PB
(全等三角形的对应边相等)
己知:如图,MN⊥AB,垂足为C,且AC=BC,P为MN上的任意一点
求证:PA=PB
C
A
B
∟
P
线段垂直平分线上的 到
的距离相等.
点
这条线段两个端点
M
N
自学检测1 (6分钟)
2、在△ABC中,PM,QN分别垂直平分AB,AC,
若BC=10cm,则△APQ的周长=___cm
若∠BAC=100°则∠PAQ=____
10
200
1.如图1,已知直线MN是线段AB的垂直平分线,垂足为D,点P是MN上一点,若AB=10cm,则BD = _______cm;若PA=10cm,则PB = ______cm.
5
10
自学教材P22-P23内容,完成下面问题:
自学指导2(1分钟)
学生自学,教师巡视(4分钟)
1、判定定理:
线段垂直平分线性质定理的逆命题是:
到________________距离相等的_____,
在这条线段的垂直平分线上。它是_____命题。
一条线段两个端点
点
真
2、认真阅读例1并思考:如何证明一条直线是
一条线段的垂直平分线?
证明:到一条线段两个端点距离相等
的点,在这条线段的垂直平分线上.
证明:过P作AB的垂线交AB于C,
在Rt △PAC和Rt △PBC中,
PA=PB,PC=PC
∴ Rt △PAC≌Rt △PBC
∴AC=BC
∴PC为AB的垂直平分线
即点P在线段AB的垂直平分线上
己知:如图,PA=PB
求证:点P在线段AB的垂直平分线上
C
A
B
∟
P
自学检测2 (6分钟)
1.判定定理:
线段垂直平分线性质定理的逆命题是:
到________________距离相等的 ,
在这条线段的垂直平分线上。它是 命题。
一条线段两个端点
点
真
2、如图,AB是线段CD的垂直平分线,
E,F是AB上的两点.
求证:∠ECF=∠EDF
A
F
D
E
B
C
证明:∵AB是线段CD的垂直平分线
∴CE=DE,CF=DF
∴∠ECD=∠EDC,∠FCD=∠FDC
∴ ∠ECD+∠FCD=∠EDC+∠FDC
即∠ECF=∠EDF
定理:线段垂直平分线上的点到这条线段两个端点的距离相等。
如图,
∵点P在线段AB的垂直平分线上
∴PA=PB
文字语言
符号语言
学生讨论,更正,老师点拨 (4分钟)
P
A
B
∟
线段垂直平分线的性质定理
图形语言
定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
如图,
∵ PA=PB
∴点P在线段AB的垂直平分线上
文字语言
符号语言
P
A
B
∟
线段垂直平分线的判定定理
C
图形语言
解决“问题引入”
学校
超市
H
当堂训练(15分钟)
1、已知MN是线段AB的垂直平分线,C,D是MN上的两点,
∠CAB=60°,∠DAB=20°,则∠CAD的度数为
2、习题1.7 T1 , T2,T3,T4
40°或80°
4. (选做题)如图,DE,DF分别是 △ABD和△ACD的高,
且DE﹦DF. 求证:AD垂直平分EF
O
F
E
D
C
B
A
当堂训练(15分钟)
T2:所有等腰三角形的顶点都在线段AB的垂 直平分线上。
T3:BC长为23.
T4:解:
.
.
.
∴点P为所求作
T1:60°
2、习题1.7 T1 ,T3,T4
A
B
如何作已知线段的中垂线?
P
T1.在三角形ABC中,AB=AC,∠BAC=120°,AB的垂直平分线
交AB于点E,交BC于点D,连接AF,求∠AFC的度数.
证明:∵在三角形ABC中,AB=AC,∠BAC=120?,
∴∠∠B=∠C=30?
∵EF为AB的垂直平分线
∴BF=AF,∠BAF=∠B=30?
∴∠CAF=90?
∵∠C=30?
∴ ∠AFC=60°
T3.如图,在△ABC中,已知AC=27,AB的垂直平分线交AB于
点D,交AC于点E,△BCE的周长等于50,求BC的长.
解:∵AB的垂直平分线交AB于点D,交AC于点E,
∴AE=BE,
∴AC=AE+EC=BE+EC=27.
∵ △BCE的周长等于50
∴BE+EC+BC=50
∴BC=50-27=23.
4. (选做题)如图,DE,DF分别是 △ABD和△ACD的高,
且DE﹦DF. 求证:AD垂直平分EF
证明:
∵DE⊥AB,DF⊥AC
∴△AED和△AFD是直角三角形
又∵DE=DF,AD=AD
∴Rt△AED≌Rt△AFD(HL)
∴AE=AF
∴点A在EF的垂直平分线上
∵DE=DF
∴点D在EF的垂直平分线上
∴AD垂直平分EF
O
F
E
D
C
B
A
板书设计
1、线段垂直平分线的性质定理
2、应用线段垂直平分线的判定定理
1.3.1线段的垂直平分线
问题引入
第一章 三角形的证明
1.3.1 线段的垂直平分线
八年级数学
主备人:
议课组:第2议课组
议课时间:. 2月 28日
授课时间:第二周 3月10日
学习目标(1分钟)
1.会证明线段垂直平分线的性质定理和判定定理.
2.会用线段垂直平分线的性质定理和判定定理解决问题
自学教材P22“想一想”之前的内容,完成下面问题:
自学指导1(1分钟)
学生自学,教师巡视(6分钟)
2、你能证明线段垂直平分线定理吗?你能用数学符号语言表达出来吗?
1、线段垂直平分线性质定理:
线段垂直平分线上的 到
的距离相等.
点
这条线段两个端点
提示:画图,写出已知、求证和证明过程。
证明:∵ MN⊥AB
∴∠PCA=∠PCB=90°
∵ AC=BC,PC=PC
∴△PAC≌△PBC(SAS)
∴PA=PB
(全等三角形的对应边相等)
己知:如图,MN⊥AB,垂足为C,且AC=BC,P为MN上的任意一点
求证:PA=PB
C
A
B
∟
P
线段垂直平分线上的 到
的距离相等.
点
这条线段两个端点
M
N
自学检测1 (6分钟)
2、在△ABC中,PM,QN分别垂直平分AB,AC,
若BC=10cm,则△APQ的周长=___cm
若∠BAC=100°则∠PAQ=____
10
200
1.如图1,已知直线MN是线段AB的垂直平分线,垂足为D,点P是MN上一点,若AB=10cm,则BD = _______cm;若PA=10cm,则PB = ______cm.
5
10
自学教材P22-P23内容,完成下面问题:
自学指导2(1分钟)
学生自学,教师巡视(4分钟)
1、判定定理:
线段垂直平分线性质定理的逆命题是:
到________________距离相等的_____,
在这条线段的垂直平分线上。它是_____命题。
一条线段两个端点
点
真
2、认真阅读例1并思考:如何证明一条直线是
一条线段的垂直平分线?
证明:到一条线段两个端点距离相等
的点,在这条线段的垂直平分线上.
证明:过P作AB的垂线交AB于C,
在Rt △PAC和Rt △PBC中,
PA=PB,PC=PC
∴ Rt △PAC≌Rt △PBC
∴AC=BC
∴PC为AB的垂直平分线
即点P在线段AB的垂直平分线上
己知:如图,PA=PB
求证:点P在线段AB的垂直平分线上
C
A
B
∟
P
自学检测2 (6分钟)
1.判定定理:
线段垂直平分线性质定理的逆命题是:
到________________距离相等的 ,
在这条线段的垂直平分线上。它是 命题。
一条线段两个端点
点
真
2、如图,AB是线段CD的垂直平分线,
E,F是AB上的两点.
求证:∠ECF=∠EDF
A
F
D
E
B
C
证明:∵AB是线段CD的垂直平分线
∴CE=DE,CF=DF
∴∠ECD=∠EDC,∠FCD=∠FDC
∴ ∠ECD+∠FCD=∠EDC+∠FDC
即∠ECF=∠EDF
定理:线段垂直平分线上的点到这条线段两个端点的距离相等。
如图,
∵点P在线段AB的垂直平分线上
∴PA=PB
文字语言
符号语言
学生讨论,更正,老师点拨 (4分钟)
P
A
B
∟
线段垂直平分线的性质定理
图形语言
定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
如图,
∵ PA=PB
∴点P在线段AB的垂直平分线上
文字语言
符号语言
P
A
B
∟
线段垂直平分线的判定定理
C
图形语言
解决“问题引入”
学校
超市
H
当堂训练(15分钟)
1、已知MN是线段AB的垂直平分线,C,D是MN上的两点,
∠CAB=60°,∠DAB=20°,则∠CAD的度数为
2、习题1.7 T1 , T2,T3,T4
40°或80°
4. (选做题)如图,DE,DF分别是 △ABD和△ACD的高,
且DE﹦DF. 求证:AD垂直平分EF
O
F
E
D
C
B
A
当堂训练(15分钟)
T2:所有等腰三角形的顶点都在线段AB的垂 直平分线上。
T3:BC长为23.
T4:解:
.
.
.
∴点P为所求作
T1:60°
2、习题1.7 T1 ,T3,T4
A
B
如何作已知线段的中垂线?
P
T1.在三角形ABC中,AB=AC,∠BAC=120°,AB的垂直平分线
交AB于点E,交BC于点D,连接AF,求∠AFC的度数.
证明:∵在三角形ABC中,AB=AC,∠BAC=120?,
∴∠∠B=∠C=30?
∵EF为AB的垂直平分线
∴BF=AF,∠BAF=∠B=30?
∴∠CAF=90?
∵∠C=30?
∴ ∠AFC=60°
T3.如图,在△ABC中,已知AC=27,AB的垂直平分线交AB于
点D,交AC于点E,△BCE的周长等于50,求BC的长.
解:∵AB的垂直平分线交AB于点D,交AC于点E,
∴AE=BE,
∴AC=AE+EC=BE+EC=27.
∵ △BCE的周长等于50
∴BE+EC+BC=50
∴BC=50-27=23.
4. (选做题)如图,DE,DF分别是 △ABD和△ACD的高,
且DE﹦DF. 求证:AD垂直平分EF
证明:
∵DE⊥AB,DF⊥AC
∴△AED和△AFD是直角三角形
又∵DE=DF,AD=AD
∴Rt△AED≌Rt△AFD(HL)
∴AE=AF
∴点A在EF的垂直平分线上
∵DE=DF
∴点D在EF的垂直平分线上
∴AD垂直平分EF
O
F
E
D
C
B
A
板书设计
1、线段垂直平分线的性质定理
2、应用线段垂直平分线的判定定理
1.3.1线段的垂直平分线
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
