3.5力的分解(共26张ppt)
文档属性
| 名称 | 3.5力的分解(共26张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-02-28 16:24:57 | ||
图片预览










文档简介
(共31张PPT)
1、合力和分力是等效替代关系(合力和分力不能同时作用在物体上)
2、合力和分力满足平行四边形定则,不存在必然的大小关系(2个力或3个力合力的范围)
3、验证平行四边形定则实验的步骤及
注意事项
一个力产生的效果跟几个力共同产生的效果相同,这个力叫做那几个力的合力。原来的几个力叫做分力。
求几个已知力的合力叫做力的合成。
力的合成
在实际问题中,就可以用这个力来代替那几个力,这就是力的等效代替。而不是物体又多受了一个合力。
力的合成就是找一个力去代替几个已知力,而不是改变其作用效果
实验步骤
1、把方木板放在桌上,用图钉把白纸钉在方木板上
2、用图钉把橡皮条的一端固定在方木板上A点,橡皮条的另一端B拴上两根细绳
3、用两把弹簧秤分别钩住两根细绳,沿两个不同方向拉橡皮条,使橡皮条的结点B伸长到某一位置O点,记下O点的位置、两把弹簧秤的读数和两根细绳的方向
4、用一把弹簧秤钩住一根细绳,使橡皮条的结点B拉到同样位置O点,记下弹簧秤的读数和细绳的方向
5、选定一个合适的标度,用力的图示法画出F1、F2和F的图示
为什么要记下细绳的方向?
为什么也要拉到同样的位置?
能否先做步骤4再做步骤3?
练习3
三个力的合力范围怎么求?
①3N、4N、5N;
②2N、5N、6N;
③8N、4N、3N;
④1N、5N、9N;
最大值:F合=F1+F2+F3
最小值:
①先求任两个力F1、F2合力大小范围:
︱F1-F2︱≤
F
≤F1+F2;
②若F3在此范围内,三个力的合力最小值为0。
③若F3不在此范围内,三个力的合力最大力减去另外两个的合力最大值。
①0N≤F≤12N;
②0N≤F≤13N;
③1N≤F≤15N;
④3N≤F≤15N;
例1、3N和4N,两个的合力那些是可能的?
A、1N
B、2N
C、3N
D、4N
E、5N F、6N
例2、(1)3N、4N和5N三个力,合力的最大值
和最小值是多大?
(2)3N、4N和3N三个力,合力的最大值
和最小值是多大?
(3)3N、4N和8N三个力,合力的最大值
和最小值是多大?
力的分解
F2
F1
F
F1
F2
·
F
什么是力的分解
★用几个分力来等效替代一个力
1
合力F
分力F1和F2
合成
分解
等效替代
★求一个力的分力叫做力的分解
一、力的分解法则
1.阅读课本
(1)、图中的拖拉机对耙的拉力起到了什么效果??
(2)、图中什么是分力?什么是合力?
(3)、力的分解遵循什么定则?为什么?
思考
2.探索
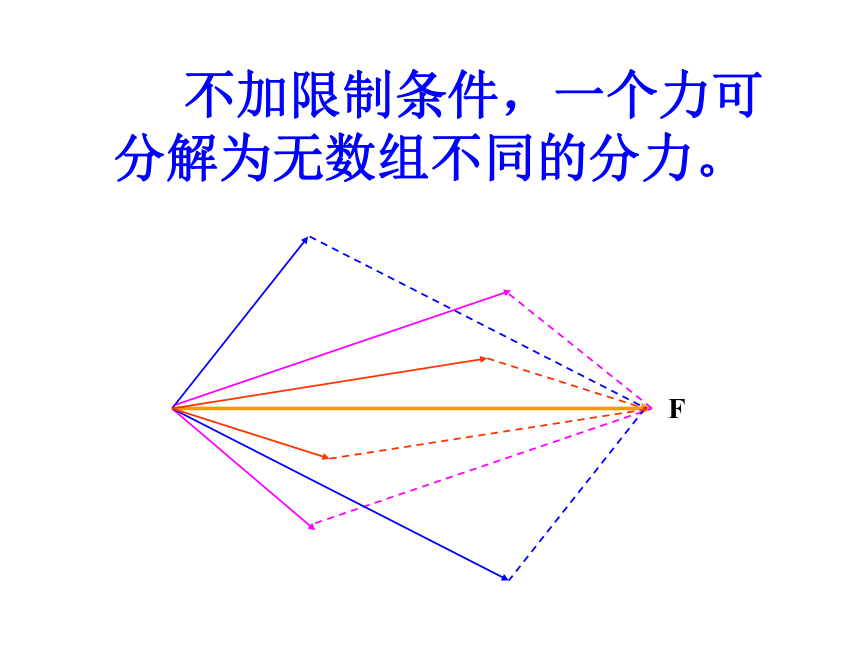
如果没有条件限制,同一条对角线可以作出几个不同的平行四边形??
不加限制条件,一个力可分解为无数组不同的分力。
F
二、力的分解原则
(1)由于分力和合力相互替代的前提是相同的作用效果,所以在分解力时其各个分力必须有各自的实际效果
(2)力的分解原则:将力按所
产生的实际作用效果进行分解
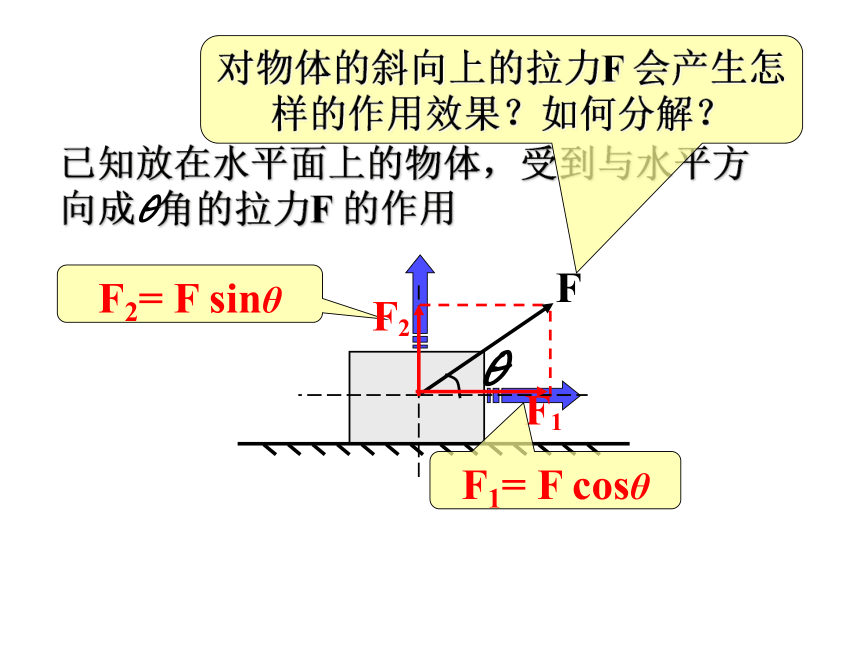
已知放在水平面上的物体,受到与水平方向成θ角的拉力F
的作用
对物体的斜向上的拉力F
会产生怎样的作用效果?如何分解?
F2=
F
sinθ
θ
F
F1
F2
F1=
F
cosθ
练习、如图所示,质量为m的木块在力F作用下在水平面上做匀速运动。木块与地面间的动摩擦因数为?,则物体受到的摩擦力为
(
)
?
F
?mg
?(mg+Fsin?)
?(mg-Fsin?)
Fcos?
BD
倾角为θ的斜面上放有一个物体,如图所示。该物体受到的重力G能对物体产生那些效果?应当怎样分解重力?分力的大小各是多大?
G2
G1
θ
G
θ
高大的桥要造很长的引桥,来减小桥面的倾角
已知放在斜面上的物体所受重力为G,斜面倾角为θ
θ
放在斜面上的物体所受重力G产生怎样的作用效果?如何分解?
F2=
G
cosθ
G
F1
F2
θ
θ
F1
F2
G
θ
F1=
G
sinθ
F1=
G
tanθ
F2=
G/cosθ
力分解的步骤:
4、据三角形知识求分力的大小和方向.
3、用平行四边形定则定分力的大小;
(把力F作为对角线,画平行四边形得分力)
1、分析力的作用效果;
2、据力的作用效果定分力的方向;
(画两个分力的方向)
M
G
T1
T2
O
N
370
530
T
把的物体挂在成角度的两根细绳MO,
NO上,易知物体对悬点O的拉力T等于物体所
受的重力G。如图所示,怎样把力T按其作用
效果分解?它的两个分力的大小、方向如何?
(sin370=0.6,
cos370=0.8)
370
用两根轻绳将物体悬挂起来。已知物体重力为G,轻绳AO与水平方向夹角为θ,AOB为直角
例3
F1=
G
cosθ
F2=
G
sinθ
悬挂着的物体所受重力G产生怎样的作用效果?如何分解?
θ
F1
F2
G
θ
A
B
O
T
T1
T2
θ
在竖直墙上固定一个轻支架,横杆OM垂直于墙壁,斜杆ON跟墙的夹角为θ,在支架的O点挂有一个重为G的物体,如图所示。怎样确定杆OM、ON的受力方向?
O
M
N
θ
讨论:
用一只钩码,能使细绳产生比钩码的重力大的拉力吗?
F1
F2
F
帆船为什么能逆风前进?
二、矢量相加的法则
1、平行四边形定则
[探求]
人从A到B,再到C的过程中,总位移与两段位移的关系。
A
B
C
X1
X2
X
二、力的分解的解法
2、已知合力和一个分力的大小和方向,求另一个分力的大小和方向。
1、已知合力和两个分力的方向,求两个分力的大小。
o
F
F1
F2
O
F
F1
F2
以上的解法唯一确定
3、已知合力及一个分力的大小和另一个分力的方向
F2
F1
F
θ
①当F2②当F2=Fsinθ时
③当Fsinθ④当F2>F时
讨论
无解
一组解
两组解
一组解
巩固练习
1、一个力,如果它的两个分力的作用线已经给定,分解结果可能有
种(注意:两分力作用线与该力作用线不重合)
1
2、一个水平向右的80N的力分解为两个分力,一个分力竖直向下大小为60N,求另一个分力的大小和方向。
F
0
F1
F2
3、有一个力大小为100N,将它分解为两个力,已知它的一个分力方向与该力方向的夹角为30°。那么,它的另一个分力的最小值是
N,与该力的夹角为
。
50
60°
30°
四、力的正交分解
在很多问题中,常把一个力分解为互相垂直的两个分力,特别是物体受多个力作用时,把物体受到的各个力都分解到互相垂直的两个方向上去,然后求两个方向上的力的合力,这样可把复杂问题简化,尤其是在求多个力的合力时,用正交分解的方法,先将力分解再合成非常简单.
怎样去选取坐标呢?原则上是任意的,实际问题中,让尽可能多的力落在这个方向上,这样就可以尽可能少分解力.
如图所示,将力F沿力x、y方向分解,可得:
放在水平面上的物体受到一个斜向上的拉力F的作用,该力与水平方向夹角为θ,这个力产生两个效果:水平向前拉物体,同时竖直向上提物体,因此力F可以分解为沿水平方向的分力F1和沿着竖直方向的分力F2
,力F1和力F2的大小为:
例题1
F1=Fcosθ F2=Fsinθ
θ
F
F
θ
F1
F2
X
Y
一、力的分解遵守平行四边形定则
1、定
解
条
件
(1)已知两分力的方向
(2)已知一个分力的大小和方向
2、效果分解法
(1)
据力的作用效果定分力的方向;
(2)
用平行四边形定则定分力的大小;
(3)据三角形知识求分力的大小和方向.
3、正交分解法:沿两互相垂直的方向分解
1、合力和分力是等效替代关系(合力和分力不能同时作用在物体上)
2、合力和分力满足平行四边形定则,不存在必然的大小关系(2个力或3个力合力的范围)
3、验证平行四边形定则实验的步骤及
注意事项
一个力产生的效果跟几个力共同产生的效果相同,这个力叫做那几个力的合力。原来的几个力叫做分力。
求几个已知力的合力叫做力的合成。
力的合成
在实际问题中,就可以用这个力来代替那几个力,这就是力的等效代替。而不是物体又多受了一个合力。
力的合成就是找一个力去代替几个已知力,而不是改变其作用效果
实验步骤
1、把方木板放在桌上,用图钉把白纸钉在方木板上
2、用图钉把橡皮条的一端固定在方木板上A点,橡皮条的另一端B拴上两根细绳
3、用两把弹簧秤分别钩住两根细绳,沿两个不同方向拉橡皮条,使橡皮条的结点B伸长到某一位置O点,记下O点的位置、两把弹簧秤的读数和两根细绳的方向
4、用一把弹簧秤钩住一根细绳,使橡皮条的结点B拉到同样位置O点,记下弹簧秤的读数和细绳的方向
5、选定一个合适的标度,用力的图示法画出F1、F2和F的图示
为什么要记下细绳的方向?
为什么也要拉到同样的位置?
能否先做步骤4再做步骤3?
练习3
三个力的合力范围怎么求?
①3N、4N、5N;
②2N、5N、6N;
③8N、4N、3N;
④1N、5N、9N;
最大值:F合=F1+F2+F3
最小值:
①先求任两个力F1、F2合力大小范围:
︱F1-F2︱≤
F
≤F1+F2;
②若F3在此范围内,三个力的合力最小值为0。
③若F3不在此范围内,三个力的合力最大力减去另外两个的合力最大值。
①0N≤F≤12N;
②0N≤F≤13N;
③1N≤F≤15N;
④3N≤F≤15N;
例1、3N和4N,两个的合力那些是可能的?
A、1N
B、2N
C、3N
D、4N
E、5N F、6N
例2、(1)3N、4N和5N三个力,合力的最大值
和最小值是多大?
(2)3N、4N和3N三个力,合力的最大值
和最小值是多大?
(3)3N、4N和8N三个力,合力的最大值
和最小值是多大?
力的分解
F2
F1
F
F1
F2
·
F
什么是力的分解
★用几个分力来等效替代一个力
1
合力F
分力F1和F2
合成
分解
等效替代
★求一个力的分力叫做力的分解
一、力的分解法则
1.阅读课本
(1)、图中的拖拉机对耙的拉力起到了什么效果??
(2)、图中什么是分力?什么是合力?
(3)、力的分解遵循什么定则?为什么?
思考
2.探索
如果没有条件限制,同一条对角线可以作出几个不同的平行四边形??
不加限制条件,一个力可分解为无数组不同的分力。
F
二、力的分解原则
(1)由于分力和合力相互替代的前提是相同的作用效果,所以在分解力时其各个分力必须有各自的实际效果
(2)力的分解原则:将力按所
产生的实际作用效果进行分解
已知放在水平面上的物体,受到与水平方向成θ角的拉力F
的作用
对物体的斜向上的拉力F
会产生怎样的作用效果?如何分解?
F2=
F
sinθ
θ
F
F1
F2
F1=
F
cosθ
练习、如图所示,质量为m的木块在力F作用下在水平面上做匀速运动。木块与地面间的动摩擦因数为?,则物体受到的摩擦力为
(
)
?
F
?mg
?(mg+Fsin?)
?(mg-Fsin?)
Fcos?
BD
倾角为θ的斜面上放有一个物体,如图所示。该物体受到的重力G能对物体产生那些效果?应当怎样分解重力?分力的大小各是多大?
G2
G1
θ
G
θ
高大的桥要造很长的引桥,来减小桥面的倾角
已知放在斜面上的物体所受重力为G,斜面倾角为θ
θ
放在斜面上的物体所受重力G产生怎样的作用效果?如何分解?
F2=
G
cosθ
G
F1
F2
θ
θ
F1
F2
G
θ
F1=
G
sinθ
F1=
G
tanθ
F2=
G/cosθ
力分解的步骤:
4、据三角形知识求分力的大小和方向.
3、用平行四边形定则定分力的大小;
(把力F作为对角线,画平行四边形得分力)
1、分析力的作用效果;
2、据力的作用效果定分力的方向;
(画两个分力的方向)
M
G
T1
T2
O
N
370
530
T
把的物体挂在成角度的两根细绳MO,
NO上,易知物体对悬点O的拉力T等于物体所
受的重力G。如图所示,怎样把力T按其作用
效果分解?它的两个分力的大小、方向如何?
(sin370=0.6,
cos370=0.8)
370
用两根轻绳将物体悬挂起来。已知物体重力为G,轻绳AO与水平方向夹角为θ,AOB为直角
例3
F1=
G
cosθ
F2=
G
sinθ
悬挂着的物体所受重力G产生怎样的作用效果?如何分解?
θ
F1
F2
G
θ
A
B
O
T
T1
T2
θ
在竖直墙上固定一个轻支架,横杆OM垂直于墙壁,斜杆ON跟墙的夹角为θ,在支架的O点挂有一个重为G的物体,如图所示。怎样确定杆OM、ON的受力方向?
O
M
N
θ
讨论:
用一只钩码,能使细绳产生比钩码的重力大的拉力吗?
F1
F2
F
帆船为什么能逆风前进?
二、矢量相加的法则
1、平行四边形定则
[探求]
人从A到B,再到C的过程中,总位移与两段位移的关系。
A
B
C
X1
X2
X
二、力的分解的解法
2、已知合力和一个分力的大小和方向,求另一个分力的大小和方向。
1、已知合力和两个分力的方向,求两个分力的大小。
o
F
F1
F2
O
F
F1
F2
以上的解法唯一确定
3、已知合力及一个分力的大小和另一个分力的方向
F2
F1
F
θ
①当F2
③当Fsinθ
讨论
无解
一组解
两组解
一组解
巩固练习
1、一个力,如果它的两个分力的作用线已经给定,分解结果可能有
种(注意:两分力作用线与该力作用线不重合)
1
2、一个水平向右的80N的力分解为两个分力,一个分力竖直向下大小为60N,求另一个分力的大小和方向。
F
0
F1
F2
3、有一个力大小为100N,将它分解为两个力,已知它的一个分力方向与该力方向的夹角为30°。那么,它的另一个分力的最小值是
N,与该力的夹角为
。
50
60°
30°
四、力的正交分解
在很多问题中,常把一个力分解为互相垂直的两个分力,特别是物体受多个力作用时,把物体受到的各个力都分解到互相垂直的两个方向上去,然后求两个方向上的力的合力,这样可把复杂问题简化,尤其是在求多个力的合力时,用正交分解的方法,先将力分解再合成非常简单.
怎样去选取坐标呢?原则上是任意的,实际问题中,让尽可能多的力落在这个方向上,这样就可以尽可能少分解力.
如图所示,将力F沿力x、y方向分解,可得:
放在水平面上的物体受到一个斜向上的拉力F的作用,该力与水平方向夹角为θ,这个力产生两个效果:水平向前拉物体,同时竖直向上提物体,因此力F可以分解为沿水平方向的分力F1和沿着竖直方向的分力F2
,力F1和力F2的大小为:
例题1
F1=Fcosθ F2=Fsinθ
θ
F
F
θ
F1
F2
X
Y
一、力的分解遵守平行四边形定则
1、定
解
条
件
(1)已知两分力的方向
(2)已知一个分力的大小和方向
2、效果分解法
(1)
据力的作用效果定分力的方向;
(2)
用平行四边形定则定分力的大小;
(3)据三角形知识求分力的大小和方向.
3、正交分解法:沿两互相垂直的方向分解
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
