7.7 动能和动能定理(共42张ppt)
文档属性
| 名称 | 7.7 动能和动能定理(共42张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-02-28 16:29:00 | ||
图片预览









文档简介
(共42张PPT)
7
动能和动能定理
动能和动能定理
7
1.知道动能的表达式,会根据动能的表达式计算运动物体的动能。
2.能用牛顿第二定律和运动学公式导出动能定理,理解动能定理的物理意义。
3.会用动能定理处理单个物体的有关问题,领会运用动能定理解题的优越性。
4.知道动能定理也可用于变力做功与曲线运动的情景,能用动能定理计算变力所做的功。
回顾:
动能的概念:
物体由于运动而具有的能量叫动能。
大胆猜测:动能跟哪些因素有关?
质量、速度
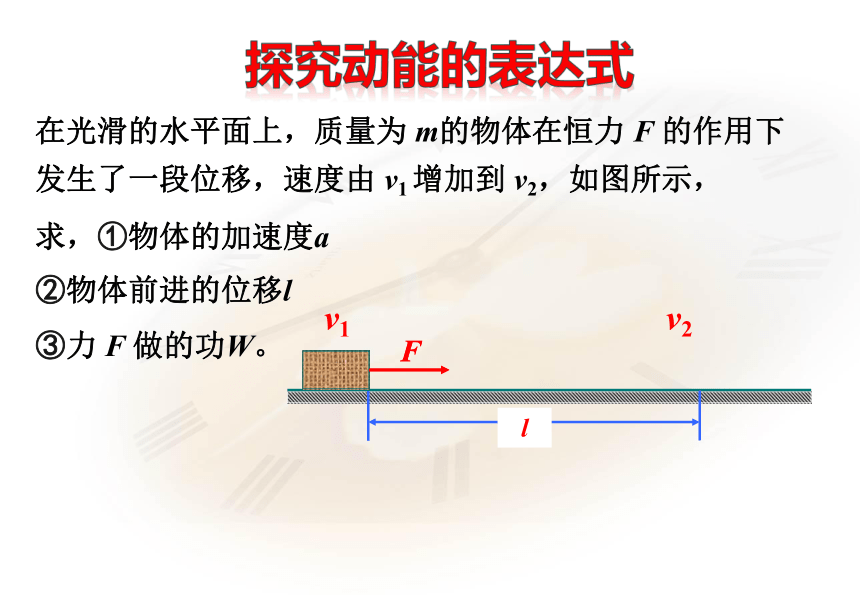
在光滑的水平面上,质量为
m的物体在恒力
F
的作用下发生了一段位移,速度由
v1
增加到
v2,如图所示,
求,①物体的加速度a
②物体前进的位移l
③力
F
做的功W。
F
F
l
v1
v2
说明:
①动能是标量,
②动能是状态量
③动能具有相对性
(与参考系的选择有关,
且只有正值。
(动能只与速度的大小有关,而与速度的方向无关)
一般选地面为参考系)
单位:焦(J)
随堂练习
下列关于一定质量的物体的速度和动能的说法中,正确的是(
)
A、速度变化,动能一定变化
B、速度不变,动能一定不变
C、动能变化,速度一定变化
D、动能不变,速度可能变化
BCD
内容:力在一个过程中对物体所做的功,等于物体在这个过程中动能的变化。
表达式
动能的增加
合力
说明:
①功是过程量,动能是状态量.涉及一个过程两个状态.
②标量式
③合力对物体做正功
合力对物体做正功
动能增加
物体动能减少
s
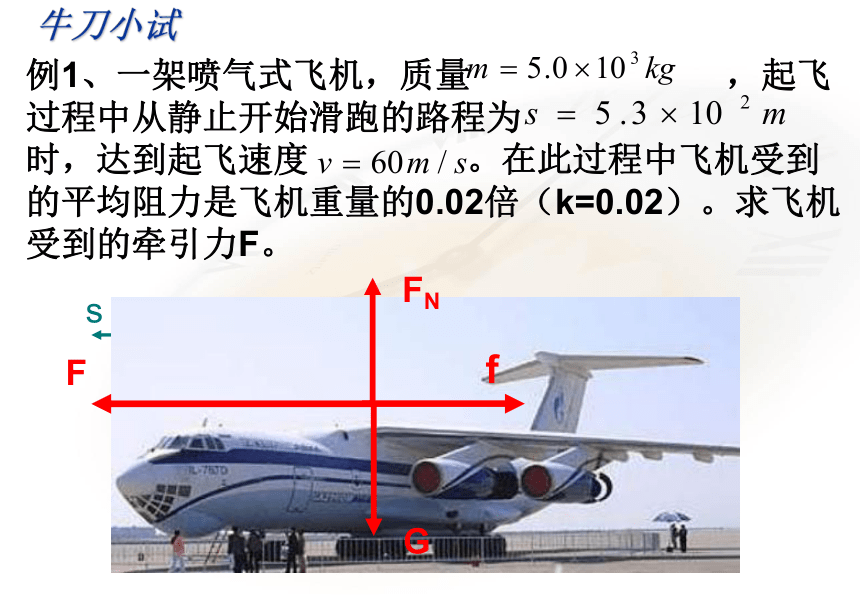
例1、一架喷气式飞机,质量
,起飞过程中从静止开始滑跑的路程为
时,达到起飞速度
。在此过程中飞机受到的平均阻力是飞机重量的0.02倍(k=0.02)。求飞机受到的牵引力F。
牛刀小试
G
FN
f
F
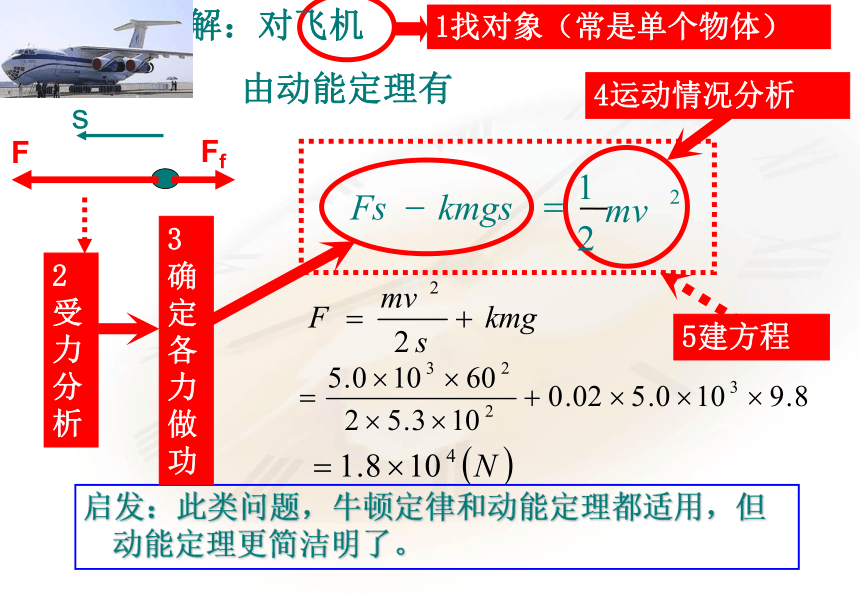
1找对象(常是单个物体)
解:对飞机
由动能定理有
启发:此类问题,牛顿定律和动能定理都适用,但动能定理更简洁明了。
s
F
Ff
3确定各力做功
4运动情况分析
5建方程
2受力分析
kmgs
Fs
1
2
2
mv
=
-
动能定理:
牛顿运动定律:
例题2:一架喷气式飞机,质量m=5.0×103kg,起飞过程中从静止开始滑跑。当位移达到l=5.3×102m时,速度达到起飞速度v=60m/s。在此过程中飞机受到的平均阻力是飞机重量的0.02倍。求飞机受到的牵引力。
F合=F-F阻=F-
kmg
=ma
②
分别用牛顿运动定律和动能定理求解
a=
2l
v2
由
v2-v02
=2al
得
①
由动能定理得
由
①②得F=
+
kmg
2l
mv2
∴F=
+
kmg
2l
mv2
W合=(F-F阻)l
=(F-kmg)l
=
mv2
1
2
既适用于恒力做功,也适用于变力做功;
既适用于直线运动,也适用于曲线运动。
适用范围:
应用动能定理解题的一般步骤:
①
明确研究对象,明确运动过程.
②分析研究对象的受力情况和各个力的做功情况:受哪些力?每个力是否做功,做正功还是做负功?做多少功?然后求各个力做功的代数和--W总
③
明确始末状态,确定其动能(EK2,
EK1)及动能变化量(△Ek)
(未知
量用符号表示),根据动能定理列出
方程:
W总=Ek2—Ek1
④
根据动能定理列方程求解并检验。
动能的表达式
合力在一个过程中对物体所做的功,等于物体在这个过程中动能的变化,这个结论叫做动能定理。
1.
合力做的功
2.
所有力做功的代数和
合力做的功
末状态动能
初状态动能
对应着一个过程
这一过程始末状态
动能的变化量
同一过程
1.当合力对物体做正功时,物体动能如何变化?
2.当合力对物体做负功时,物体动能如何变化?
物体动能增加
物体动能减少
1.
明确研究对象及所研究的物理过程。
2.
对研究对象进行受力分析,并确定各力所做的功,求出所有力的总功。
4.
求解方程、分析结果。
FN
例1.一架喷气式飞机,质量
m=1×104
kg,当起飞过程中从静止开始滑跑的路程为
l
=
5×102
m时,达到起飞速度
v
=
60
m/s,在此过程中飞机受到的平均阻力是飞机重量的
k
倍(
k
=0.02),求飞机受到的牵引力。
G
f
F
解:①常规方法
②动能定理法
例2.
一辆质量为
m,速度为
v0
的汽车,关闭发动机后在水平地面滑行了距离
l
后停下来,试求汽车受到的阻力。
动能定理不涉及物体运动过程中的加速度和时间,而只与物体的初末状态有关,因此用它处理问题有时比较方便。
动能定理对应的是一个过程,只涉及物体初、末状态的动能和整个过程合力做的总功,无需关心中间运动过程的细节,而且功和动能都是标量无方向性,计算方便,因此当题目中不涉及
a
和
t,而涉及
f、l、m、v、W、Ek
等物理量时,优先考虑使用动能定理。
适用范围广泛:
恒力做功、变力做功都可以适用
物体做直线运动、曲线运动也都可以适用
1.
一个小球从高处自由落下,则球在下落过程中的动能
(
)
A.
与它下落的距离成正比
B.
与它下落距离的平方成正比
C.
与它运动的时间成正比
D.
与它运动时间的平方成正比
AD
2.
如图所示是滑道压力测试的示意图,光滑圆弧轨道与光滑斜面相切,滑道底部
B
处安装一个压力传感器,其示数
N
表示该处所受压力的大小,某滑块从斜面上不同高度
h
处由静止下滑,通过
B
时,下列表述正确的有
(
)
A.
N
小于滑块重力
B.
N
大于滑块重力
C.
N
越大表明
h
越大
D.
N
越大表明
h
越小
BC
F
G
FN
f
3.
汽车在水平的高速公路上做匀加速直线运动,通过
100
m
的距离后,速度由
10
m/s
增加到
30
m/s,汽车的质量为2×103
kg,汽车前进时所受的阻力为车重的
0.02
倍,求汽车牵引力所做的功以及牵引力的大小。
8.4×105
J
8.4×103
N
4.
质量为
8
g
的子弹以
400
m/s的速度水平射入厚度为
5
cm
的钢板,射出后的速度为
100
m/s,求子弹克服阻力所做的功以及子弹受到的平均阻力。
─
600
J
1.2×104
N
v
v0
f
(6)适用范围:
(5)物理意义:
合力的功是动能变化的原因,
也是动能变化的量度。
既适用于恒力做功,也适用于变力做功;
既适用于直线运动,也适用于曲线运动。
例:一架喷气式飞机,质量m
=5×103kg,起飞过程中从静止开始滑跑的路程为s
=5.3×102m时,达到起飞的速度
v
=60m/s,在此过程中飞机受到的平均阻力是飞机重力的0.02倍(k=0.02),求飞机受到的牵引力。
v0=0m/s
v=60m/s
s=5.3×102m
F
f
N
G
v0=0m/s
v=60m/s
s=5.3×102m
F
f
N
G
s
例1、一架喷气式飞机,质量
,起飞过程中从静止开始滑跑的路程为
时,达到起飞速度
。在此过程中飞机受到的平均阻力是飞机重量的0.02倍(k=0.02)。求飞机受到的牵引力F。
应用1:恒力+直线运动
G
FN
f
F
1找对象(常是单个物体)
解:对飞机
由动能定理有
启发:此类问题,牛顿定律和动能定理都适用,但动能定理更简洁明了。
s
F
Ff
3确定各力做功
4运动情况分析
5建方程
2受力分析
kmgs
Fs
1
2
2
mv
=
-
3、应用动能定理解题的一般步骤
(尤其用于变力做功与曲线运动):
(1)明确对象和过程:
(2)做两方面的分析:
①受力分析,
②确定初、末状态,
(3)由动能定理列方程:
W合=
(通常是单个物体)
求各力的功及其正负,写出总功。
写出初、末态的动能。
mv22/2-mv12/2
足球运动员用力踢质量为0.3kg的静止足球,使足球以10m/s的速度飞出,假定脚踢足球时对足球的平均作用力为400N,球在水平面上运动了20m后停止,那么人对足球做的功为:
A、8000J
B、4000J
C、15J
D、无法确定
例4、在h高处,以初速度v0向水平方向抛出一小球,不计空气阻力,小球着地时速度大小为(
)
C
应用2:恒力+曲线运动
物理过程中不涉及到加速度和时间,而只与物体的初末状态有关的力学问题,优先应用动能定理。
一质量为?m的小球,用长为L的轻绳悬挂于O点。小球在水平拉力F作用下,从平衡位置P点很缓慢地移动到Q点,细线偏离竖直方向的角度为θ,如图所示。则拉力F做的功是:
A.
mgLcosθ
B.
mgL(1-cosθ)
C.
FLcosθ
D.
FL
应用3:变力做功
运动员用力将一质量为m的铅球从离地为h高处以初速度v0水平推出,当它落到地面时速度为v,则在此过程中铅球克服空气阻力所做的功等于:
A、mgh-mv2/2-mv02/2
B、mv2/2-mv02/2-mgh
C、mgh+mv02/2-mv2/2
D、mgh+mv2/2-mv02/2
G
H
h
应用4:多过程
一球从高出地面H处由静止自由落下,不考虑空气阻力,落到地面后并深入地面h深处停止,若球的质量为m,求:球在落入地面以下的过程中受到的平均阻力。
如图4所示,AB为1/4圆弧轨道,半径为R=0.8m,BC是水平轨道,长l=3m,BC处的摩擦系数为μ=1/15,今有质量m=1kg的物体,自A点从静止起下滑到C点刚好停止。求物体在轨道AB段所受的阻力对物体做的功。
高考是怎样考的
一物块由静止开始从粗糙斜面上的某点加速下滑到另一点,在此过程中重力对物块做的功等于(05辽宁):
A.物块动能的增加量
B.物块重力势能的减少量与物块克服摩擦力做的功之和
C.物块重力势能的减少量和物块动能的增加量以及物块克服摩擦力做的功之和
D.物块动能的增加量与物块克服摩擦力做的功之和
同一物体分别从高度相同,倾角不同的光滑斜面的顶端滑到底端时,相同的物理量是:
A.动能
B.速度
C.速率
D.重力所做的功
7
动能和动能定理
动能和动能定理
7
1.知道动能的表达式,会根据动能的表达式计算运动物体的动能。
2.能用牛顿第二定律和运动学公式导出动能定理,理解动能定理的物理意义。
3.会用动能定理处理单个物体的有关问题,领会运用动能定理解题的优越性。
4.知道动能定理也可用于变力做功与曲线运动的情景,能用动能定理计算变力所做的功。
回顾:
动能的概念:
物体由于运动而具有的能量叫动能。
大胆猜测:动能跟哪些因素有关?
质量、速度
在光滑的水平面上,质量为
m的物体在恒力
F
的作用下发生了一段位移,速度由
v1
增加到
v2,如图所示,
求,①物体的加速度a
②物体前进的位移l
③力
F
做的功W。
F
F
l
v1
v2
说明:
①动能是标量,
②动能是状态量
③动能具有相对性
(与参考系的选择有关,
且只有正值。
(动能只与速度的大小有关,而与速度的方向无关)
一般选地面为参考系)
单位:焦(J)
随堂练习
下列关于一定质量的物体的速度和动能的说法中,正确的是(
)
A、速度变化,动能一定变化
B、速度不变,动能一定不变
C、动能变化,速度一定变化
D、动能不变,速度可能变化
BCD
内容:力在一个过程中对物体所做的功,等于物体在这个过程中动能的变化。
表达式
动能的增加
合力
说明:
①功是过程量,动能是状态量.涉及一个过程两个状态.
②标量式
③合力对物体做正功
合力对物体做正功
动能增加
物体动能减少
s
例1、一架喷气式飞机,质量
,起飞过程中从静止开始滑跑的路程为
时,达到起飞速度
。在此过程中飞机受到的平均阻力是飞机重量的0.02倍(k=0.02)。求飞机受到的牵引力F。
牛刀小试
G
FN
f
F
1找对象(常是单个物体)
解:对飞机
由动能定理有
启发:此类问题,牛顿定律和动能定理都适用,但动能定理更简洁明了。
s
F
Ff
3确定各力做功
4运动情况分析
5建方程
2受力分析
kmgs
Fs
1
2
2
mv
=
-
动能定理:
牛顿运动定律:
例题2:一架喷气式飞机,质量m=5.0×103kg,起飞过程中从静止开始滑跑。当位移达到l=5.3×102m时,速度达到起飞速度v=60m/s。在此过程中飞机受到的平均阻力是飞机重量的0.02倍。求飞机受到的牵引力。
F合=F-F阻=F-
kmg
=ma
②
分别用牛顿运动定律和动能定理求解
a=
2l
v2
由
v2-v02
=2al
得
①
由动能定理得
由
①②得F=
+
kmg
2l
mv2
∴F=
+
kmg
2l
mv2
W合=(F-F阻)l
=(F-kmg)l
=
mv2
1
2
既适用于恒力做功,也适用于变力做功;
既适用于直线运动,也适用于曲线运动。
适用范围:
应用动能定理解题的一般步骤:
①
明确研究对象,明确运动过程.
②分析研究对象的受力情况和各个力的做功情况:受哪些力?每个力是否做功,做正功还是做负功?做多少功?然后求各个力做功的代数和--W总
③
明确始末状态,确定其动能(EK2,
EK1)及动能变化量(△Ek)
(未知
量用符号表示),根据动能定理列出
方程:
W总=Ek2—Ek1
④
根据动能定理列方程求解并检验。
动能的表达式
合力在一个过程中对物体所做的功,等于物体在这个过程中动能的变化,这个结论叫做动能定理。
1.
合力做的功
2.
所有力做功的代数和
合力做的功
末状态动能
初状态动能
对应着一个过程
这一过程始末状态
动能的变化量
同一过程
1.当合力对物体做正功时,物体动能如何变化?
2.当合力对物体做负功时,物体动能如何变化?
物体动能增加
物体动能减少
1.
明确研究对象及所研究的物理过程。
2.
对研究对象进行受力分析,并确定各力所做的功,求出所有力的总功。
4.
求解方程、分析结果。
FN
例1.一架喷气式飞机,质量
m=1×104
kg,当起飞过程中从静止开始滑跑的路程为
l
=
5×102
m时,达到起飞速度
v
=
60
m/s,在此过程中飞机受到的平均阻力是飞机重量的
k
倍(
k
=0.02),求飞机受到的牵引力。
G
f
F
解:①常规方法
②动能定理法
例2.
一辆质量为
m,速度为
v0
的汽车,关闭发动机后在水平地面滑行了距离
l
后停下来,试求汽车受到的阻力。
动能定理不涉及物体运动过程中的加速度和时间,而只与物体的初末状态有关,因此用它处理问题有时比较方便。
动能定理对应的是一个过程,只涉及物体初、末状态的动能和整个过程合力做的总功,无需关心中间运动过程的细节,而且功和动能都是标量无方向性,计算方便,因此当题目中不涉及
a
和
t,而涉及
f、l、m、v、W、Ek
等物理量时,优先考虑使用动能定理。
适用范围广泛:
恒力做功、变力做功都可以适用
物体做直线运动、曲线运动也都可以适用
1.
一个小球从高处自由落下,则球在下落过程中的动能
(
)
A.
与它下落的距离成正比
B.
与它下落距离的平方成正比
C.
与它运动的时间成正比
D.
与它运动时间的平方成正比
AD
2.
如图所示是滑道压力测试的示意图,光滑圆弧轨道与光滑斜面相切,滑道底部
B
处安装一个压力传感器,其示数
N
表示该处所受压力的大小,某滑块从斜面上不同高度
h
处由静止下滑,通过
B
时,下列表述正确的有
(
)
A.
N
小于滑块重力
B.
N
大于滑块重力
C.
N
越大表明
h
越大
D.
N
越大表明
h
越小
BC
F
G
FN
f
3.
汽车在水平的高速公路上做匀加速直线运动,通过
100
m
的距离后,速度由
10
m/s
增加到
30
m/s,汽车的质量为2×103
kg,汽车前进时所受的阻力为车重的
0.02
倍,求汽车牵引力所做的功以及牵引力的大小。
8.4×105
J
8.4×103
N
4.
质量为
8
g
的子弹以
400
m/s的速度水平射入厚度为
5
cm
的钢板,射出后的速度为
100
m/s,求子弹克服阻力所做的功以及子弹受到的平均阻力。
─
600
J
1.2×104
N
v
v0
f
(6)适用范围:
(5)物理意义:
合力的功是动能变化的原因,
也是动能变化的量度。
既适用于恒力做功,也适用于变力做功;
既适用于直线运动,也适用于曲线运动。
例:一架喷气式飞机,质量m
=5×103kg,起飞过程中从静止开始滑跑的路程为s
=5.3×102m时,达到起飞的速度
v
=60m/s,在此过程中飞机受到的平均阻力是飞机重力的0.02倍(k=0.02),求飞机受到的牵引力。
v0=0m/s
v=60m/s
s=5.3×102m
F
f
N
G
v0=0m/s
v=60m/s
s=5.3×102m
F
f
N
G
s
例1、一架喷气式飞机,质量
,起飞过程中从静止开始滑跑的路程为
时,达到起飞速度
。在此过程中飞机受到的平均阻力是飞机重量的0.02倍(k=0.02)。求飞机受到的牵引力F。
应用1:恒力+直线运动
G
FN
f
F
1找对象(常是单个物体)
解:对飞机
由动能定理有
启发:此类问题,牛顿定律和动能定理都适用,但动能定理更简洁明了。
s
F
Ff
3确定各力做功
4运动情况分析
5建方程
2受力分析
kmgs
Fs
1
2
2
mv
=
-
3、应用动能定理解题的一般步骤
(尤其用于变力做功与曲线运动):
(1)明确对象和过程:
(2)做两方面的分析:
①受力分析,
②确定初、末状态,
(3)由动能定理列方程:
W合=
(通常是单个物体)
求各力的功及其正负,写出总功。
写出初、末态的动能。
mv22/2-mv12/2
足球运动员用力踢质量为0.3kg的静止足球,使足球以10m/s的速度飞出,假定脚踢足球时对足球的平均作用力为400N,球在水平面上运动了20m后停止,那么人对足球做的功为:
A、8000J
B、4000J
C、15J
D、无法确定
例4、在h高处,以初速度v0向水平方向抛出一小球,不计空气阻力,小球着地时速度大小为(
)
C
应用2:恒力+曲线运动
物理过程中不涉及到加速度和时间,而只与物体的初末状态有关的力学问题,优先应用动能定理。
一质量为?m的小球,用长为L的轻绳悬挂于O点。小球在水平拉力F作用下,从平衡位置P点很缓慢地移动到Q点,细线偏离竖直方向的角度为θ,如图所示。则拉力F做的功是:
A.
mgLcosθ
B.
mgL(1-cosθ)
C.
FLcosθ
D.
FL
应用3:变力做功
运动员用力将一质量为m的铅球从离地为h高处以初速度v0水平推出,当它落到地面时速度为v,则在此过程中铅球克服空气阻力所做的功等于:
A、mgh-mv2/2-mv02/2
B、mv2/2-mv02/2-mgh
C、mgh+mv02/2-mv2/2
D、mgh+mv2/2-mv02/2
G
H
h
应用4:多过程
一球从高出地面H处由静止自由落下,不考虑空气阻力,落到地面后并深入地面h深处停止,若球的质量为m,求:球在落入地面以下的过程中受到的平均阻力。
如图4所示,AB为1/4圆弧轨道,半径为R=0.8m,BC是水平轨道,长l=3m,BC处的摩擦系数为μ=1/15,今有质量m=1kg的物体,自A点从静止起下滑到C点刚好停止。求物体在轨道AB段所受的阻力对物体做的功。
高考是怎样考的
一物块由静止开始从粗糙斜面上的某点加速下滑到另一点,在此过程中重力对物块做的功等于(05辽宁):
A.物块动能的增加量
B.物块重力势能的减少量与物块克服摩擦力做的功之和
C.物块重力势能的减少量和物块动能的增加量以及物块克服摩擦力做的功之和
D.物块动能的增加量与物块克服摩擦力做的功之和
同一物体分别从高度相同,倾角不同的光滑斜面的顶端滑到底端时,相同的物理量是:
A.动能
B.速度
C.速率
D.重力所做的功
