2020-2021学年人教版七年级下册数学:5.1.2垂线课件(22张ppt)
文档属性
| 名称 | 2020-2021学年人教版七年级下册数学:5.1.2垂线课件(22张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-28 00:00:00 | ||
图片预览





文档简介
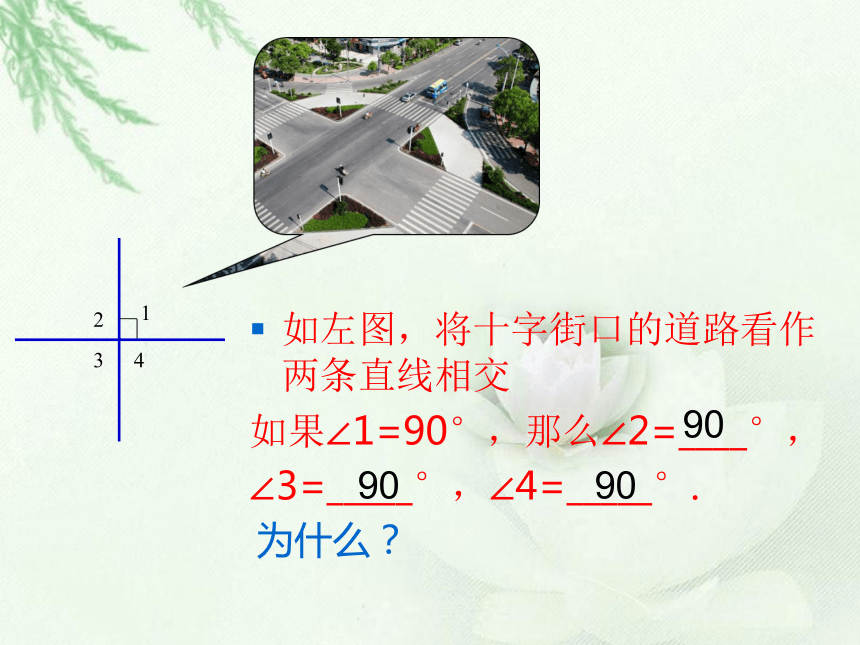
情景引入---在观察中感受:
如左图,将十字街口的道路看作两条直线相交
如果∠1=90°,那么∠2=____°,
∠3=_____°,∠4=_____°.
1
2
3
4
为什么?
90
90
90
垂直
一类特殊的相交关系
1、了解垂直的相关概念,能在生活中找到互相垂直的例子。
2、会用三角尺和折纸的方法过一点画一条直线垂直于已知直线。
3、经历探究垂线的基本事实的过程,锻炼归纳能力。
本节课学习目标
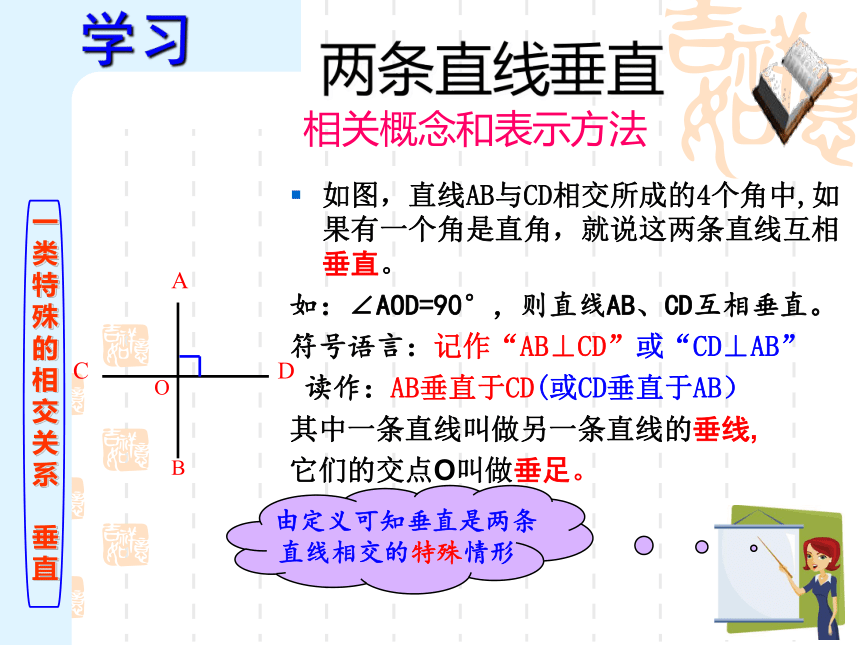
两条直线垂直
相关概念和表示方法
D
B
C
如图,直线AB与CD相交所成的4个角中,如果有一个角是直角,就说这两条直线互相垂直。
如:∠AOD=90°,则直线AB、CD互相垂直。
符号语言:记作“AB⊥CD”或“CD⊥AB”
读作:AB垂直于CD(或CD垂直于AB)
其中一条直线叫做另一条直线的垂线,
它们的交点O叫做垂足。
学习
由定义可知垂直是两条
直线相交的特殊情形
A
O
你能举一些生活中见到的垂直的实例吗?
活动探究---在实践中收获:
【动动手】如何过一点画已知直线的垂线?
P
收获1:过直线外一点有且只有一条直线与已知直线垂直。
【操作1】过直线 L外一点P画已知
直线的垂线? 如右图
1、用三角尺画垂线:
操作
别忘记画上
直角符号
回忆:点与直线有几种位置关系。
1、点在直线外
2、点在直线上
P
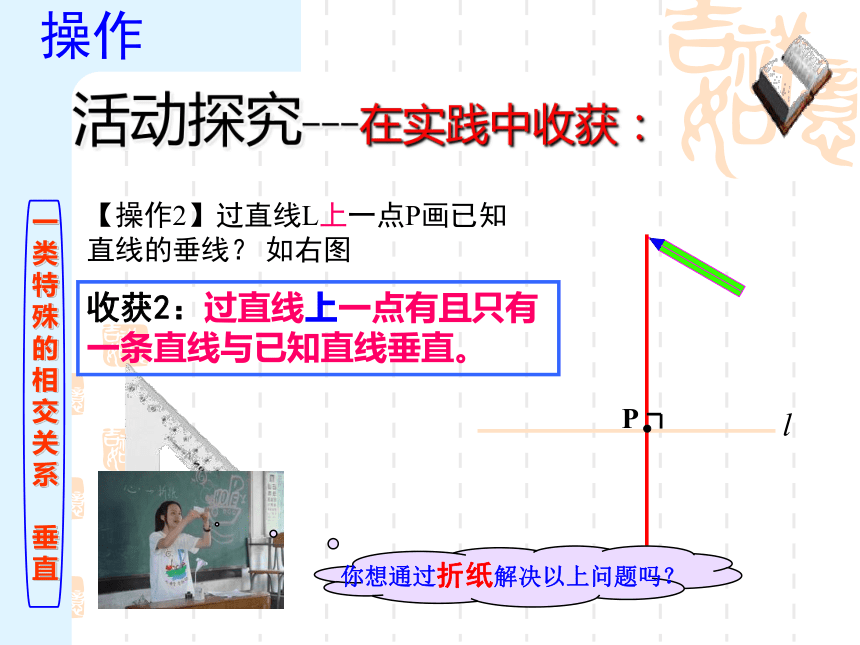
【操作2】过直线L上一点P画已知
直线的垂线? 如右图
收获2:过直线上一点有且只有一条直线与已知直线垂直。
操作
活动探究---在实践中收获:
你想通过折纸解决以上问题吗?
操作
活动探究---在实践中收获:
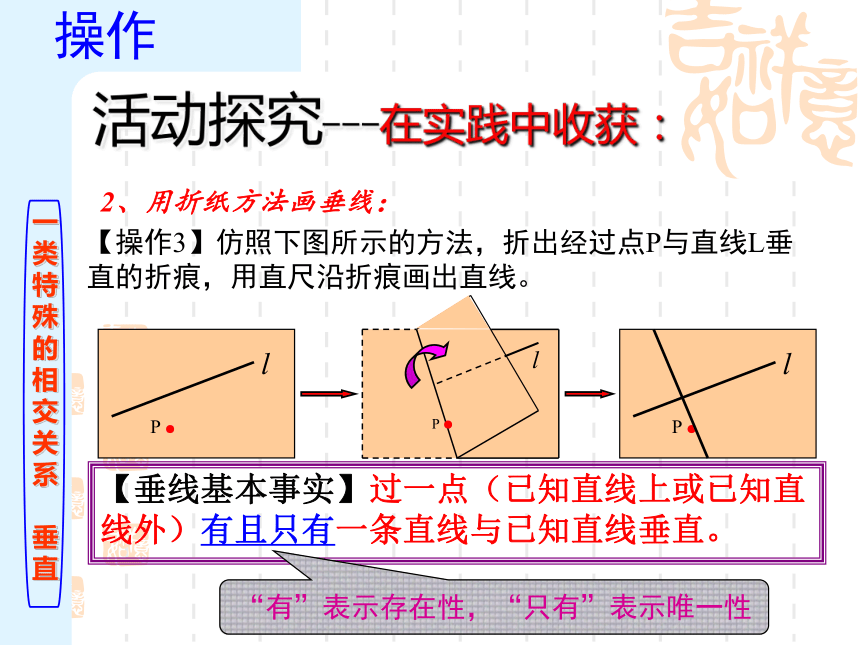
【操作3】仿照下图所示的方法,折出经过点P与直线L垂直的折痕,用直尺沿折痕画出直线。
P ●
P ●
P ●
2、用折纸方法画垂线:
【垂线基本事实】过一点(已知直线上或已知直线外)有且只有一条直线与已知直线垂直。
“有”表示存在性,“只有”表示唯一性
有时,我们说线段、射线与某一条直线互相垂直是指线段所在的直线、射线所在的直线与该直线垂直。如下图:
注意:
A
B
O
A
过P点画出线段AB的垂线、过Q点画出射线OA的垂线。
A
B
P
Q
O
A
注意:画线段(或射线)的垂线时,有时要将线段延长(或将射线反向延长)后再画垂线.
O
M
作图示范
练一练---在应用中提升:
4、如图,过点P画出∠AOB两边的垂线。
A
O
B
P
3、过点P 向线段AB 所在直线引垂线,正确的是( )
A B C D
C
练一练---在应用中提升:
P
A
B
O
A
B
点到射线或线段的垂线指的是点到射线或线段所在直线的垂线
例题解读---在应用中提升:
解:
∵∠1=35°,∠2=55°(已知)
垂直( OE⊥AB )
∴ ∠AOE=180°-∠1-∠2
= 180°-35°-55°
=90°
∴OE⊥AB (垂直的定义)
如图,已知直线AB、CD都经过O点,OE为射线,若∠1=35° ∠2=55°,则OE与AB的位置关系是________________
C
D
A
B
O
E
1
2
练一练---在应用中提升:
如图 ,已知AB. CD相交于O, OE⊥CD
于O,∠AOC=36°,则∠BOE= 。
(A)36°
(B) 64°
(C)144°
(D) 54°
A
B
O
C
D
E
54°
想一想
有人不慎掉入有鳄鱼的湖中。如图,他在P点,应选择怎样的路线才能尽快游到岸边m呢?
合作探究
(一)如图,连接直线l外一点P与直线l上各点O、
A、B、C、……
其中 ,PO为连接直线外一点与垂足形成的线段,我们称PO为点P到直线l的垂线段。
比较线段PO、PA、PB、PC……的长短,这些线段中,哪一条最短?
垂线性质2 连接直线外一点
与直线上各点的所有线段中,
垂线段最短。
简单说成: 垂线段最短。
(三)例 题
如图,一辆汽车在直线形公路AB上由A
向B行驶,M,N分别是位于公路两侧的村庄,
设汽车行驶到点P位置时,距离村庄M最近,
行驶到点Q位置时,距离村庄N最近,请在图
中公路AB上分别画出P,Q两点位置。
解:如图,过M、N两点分别作MP⊥AB,NQ⊥AB,垂足分别为P、Q,则点P、Q即为所求。
拓展应用
如图:在铁路旁边有一张庄,现在要建一火车站,为了使张庄人乘火车最方便(即距离最近),请你在铁路上选一点来建火车站,并说明理由。
张庄
∟
垂线段最短
(二)点到直线的距离
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
如图,PO的长度叫做点 P到直线l 的距离。
例题:
如图,沙坑中留下一位同学跳远的足印,如何测量这位同学的跳远成绩?为什么这样量?
∟
A
B
O
C
D
如图:已知∠ACB=90°,若BC=8,AC=6,AB=10,那么B到AC得距离是_ _ _ ,A到BC得距离是_ _ _ ,AB两点之间的距离是 _ _ _ 。
A
B
C
练 习 :
拓展---在应用中提升:
【拓展思考】如图,OA ⊥OB, ∠AOC= ∠BOD,
试分析OC与OD的位置关系?你能说明你的结论
吗?
A
B
C
D
O
如左图,将十字街口的道路看作两条直线相交
如果∠1=90°,那么∠2=____°,
∠3=_____°,∠4=_____°.
1
2
3
4
为什么?
90
90
90
垂直
一类特殊的相交关系
1、了解垂直的相关概念,能在生活中找到互相垂直的例子。
2、会用三角尺和折纸的方法过一点画一条直线垂直于已知直线。
3、经历探究垂线的基本事实的过程,锻炼归纳能力。
本节课学习目标
两条直线垂直
相关概念和表示方法
D
B
C
如图,直线AB与CD相交所成的4个角中,如果有一个角是直角,就说这两条直线互相垂直。
如:∠AOD=90°,则直线AB、CD互相垂直。
符号语言:记作“AB⊥CD”或“CD⊥AB”
读作:AB垂直于CD(或CD垂直于AB)
其中一条直线叫做另一条直线的垂线,
它们的交点O叫做垂足。
学习
由定义可知垂直是两条
直线相交的特殊情形
A
O
你能举一些生活中见到的垂直的实例吗?
活动探究---在实践中收获:
【动动手】如何过一点画已知直线的垂线?
P
收获1:过直线外一点有且只有一条直线与已知直线垂直。
【操作1】过直线 L外一点P画已知
直线的垂线? 如右图
1、用三角尺画垂线:
操作
别忘记画上
直角符号
回忆:点与直线有几种位置关系。
1、点在直线外
2、点在直线上
P
【操作2】过直线L上一点P画已知
直线的垂线? 如右图
收获2:过直线上一点有且只有一条直线与已知直线垂直。
操作
活动探究---在实践中收获:
你想通过折纸解决以上问题吗?
操作
活动探究---在实践中收获:
【操作3】仿照下图所示的方法,折出经过点P与直线L垂直的折痕,用直尺沿折痕画出直线。
P ●
P ●
P ●
2、用折纸方法画垂线:
【垂线基本事实】过一点(已知直线上或已知直线外)有且只有一条直线与已知直线垂直。
“有”表示存在性,“只有”表示唯一性
有时,我们说线段、射线与某一条直线互相垂直是指线段所在的直线、射线所在的直线与该直线垂直。如下图:
注意:
A
B
O
A
过P点画出线段AB的垂线、过Q点画出射线OA的垂线。
A
B
P
Q
O
A
注意:画线段(或射线)的垂线时,有时要将线段延长(或将射线反向延长)后再画垂线.
O
M
作图示范
练一练---在应用中提升:
4、如图,过点P画出∠AOB两边的垂线。
A
O
B
P
3、过点P 向线段AB 所在直线引垂线,正确的是( )
A B C D
C
练一练---在应用中提升:
P
A
B
O
A
B
点到射线或线段的垂线指的是点到射线或线段所在直线的垂线
例题解读---在应用中提升:
解:
∵∠1=35°,∠2=55°(已知)
垂直( OE⊥AB )
∴ ∠AOE=180°-∠1-∠2
= 180°-35°-55°
=90°
∴OE⊥AB (垂直的定义)
如图,已知直线AB、CD都经过O点,OE为射线,若∠1=35° ∠2=55°,则OE与AB的位置关系是________________
C
D
A
B
O
E
1
2
练一练---在应用中提升:
如图 ,已知AB. CD相交于O, OE⊥CD
于O,∠AOC=36°,则∠BOE= 。
(A)36°
(B) 64°
(C)144°
(D) 54°
A
B
O
C
D
E
54°
想一想
有人不慎掉入有鳄鱼的湖中。如图,他在P点,应选择怎样的路线才能尽快游到岸边m呢?
合作探究
(一)如图,连接直线l外一点P与直线l上各点O、
A、B、C、……
其中 ,PO为连接直线外一点与垂足形成的线段,我们称PO为点P到直线l的垂线段。
比较线段PO、PA、PB、PC……的长短,这些线段中,哪一条最短?
垂线性质2 连接直线外一点
与直线上各点的所有线段中,
垂线段最短。
简单说成: 垂线段最短。
(三)例 题
如图,一辆汽车在直线形公路AB上由A
向B行驶,M,N分别是位于公路两侧的村庄,
设汽车行驶到点P位置时,距离村庄M最近,
行驶到点Q位置时,距离村庄N最近,请在图
中公路AB上分别画出P,Q两点位置。
解:如图,过M、N两点分别作MP⊥AB,NQ⊥AB,垂足分别为P、Q,则点P、Q即为所求。
拓展应用
如图:在铁路旁边有一张庄,现在要建一火车站,为了使张庄人乘火车最方便(即距离最近),请你在铁路上选一点来建火车站,并说明理由。
张庄
∟
垂线段最短
(二)点到直线的距离
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
如图,PO的长度叫做点 P到直线l 的距离。
例题:
如图,沙坑中留下一位同学跳远的足印,如何测量这位同学的跳远成绩?为什么这样量?
∟
A
B
O
C
D
如图:已知∠ACB=90°,若BC=8,AC=6,AB=10,那么B到AC得距离是_ _ _ ,A到BC得距离是_ _ _ ,AB两点之间的距离是 _ _ _ 。
A
B
C
练 习 :
拓展---在应用中提升:
【拓展思考】如图,OA ⊥OB, ∠AOC= ∠BOD,
试分析OC与OD的位置关系?你能说明你的结论
吗?
A
B
C
D
O
