24.1 旋转的概念和性质(第1课时) 课件(共35张PPT)
文档属性
| 名称 | 24.1 旋转的概念和性质(第1课时) 课件(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-28 00:00:00 | ||
图片预览







文档简介
24.1 旋转
第1课时 旋转的概念和性质
24章 圆
2020-2021学年度沪科版九年级下册
1. 掌握旋转的有关概念及基本性质.(重点)
2. 能够根据旋转的基本性质解决实际问题和进行简单 作图.(难点)
学习目标
这些运动有什么共同的特点?
新课导入
旋转的概念
B
O
A
45
°
问题 观察下面的现象,它有什么特点?
观察与思考
探究新知
钟表的指针在不停地转动,从12时到4时,时针转动了______度.
120
把时针当成一个图形,那么它可以绕着中心固定点转动一定角度.
思考:怎样来定义这种图形变换?
风车风轮的每个叶片在风的吹动下转动到新的位置.
怎样来定义这种图形变换?
把叶片当成一个平面图形,那么它可以绕着平面内中心固定点转动一定角度.
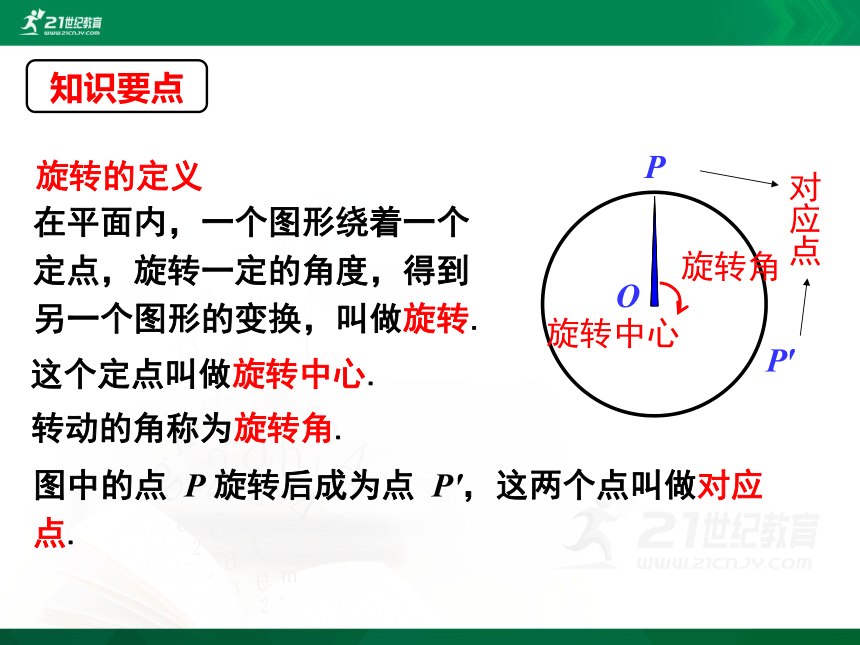
在平面内,一个图形绕着一个定点,旋转一定的角度,得到另一个图形的变换,叫做旋转.
O
P′
P
旋转中心
旋转角
对
应
点
旋转的定义
这个定点叫做旋转中心.
转动的角称为旋转角.
图中的点 P 旋转后成为点 P',这两个点叫做对应点.
知识要点
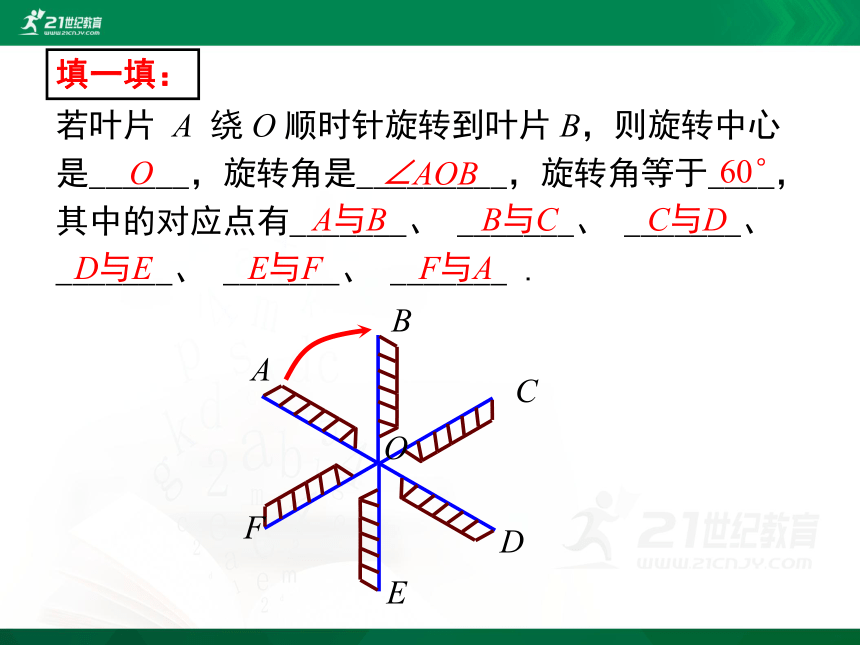
若叶片 A 绕 O 顺时针旋转到叶片 B,则旋转中心是______,旋转角是_________,旋转角等于____,其中的对应点有_______、 _______、 _______、 _______、 _______、 _______ .
O
∠AOB
60°
F与A
A与B
B与C
C与D
D与E
E与F
填一填:
A
C
D
E
F
B
O
旋转中心
旋转角
旋转方向
必须明确
确定一次图形的旋转时,
注意:①旋转的范围是“平面内”,其中“旋转中心、
旋转方向、旋转角度”称为旋转的三要素;
②旋转变换同样属于全等变换.
归纳:
A.30°
B.45°
C.90°
D.135°
例1 如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点O按逆时针方向旋转到△COD的位置,则旋转的角度为 ( )
解析:对应点与旋转中心的连线的夹角,就是旋转角,由图可知,OB、OD是对应边,∠BOD是旋转角,所以,旋转角为90°.故选C.
C
C
D
A
B
O
例题讲解
旋转的性质
A
B
B′
A′
C
.
M′
M
.
.
.
.
45°
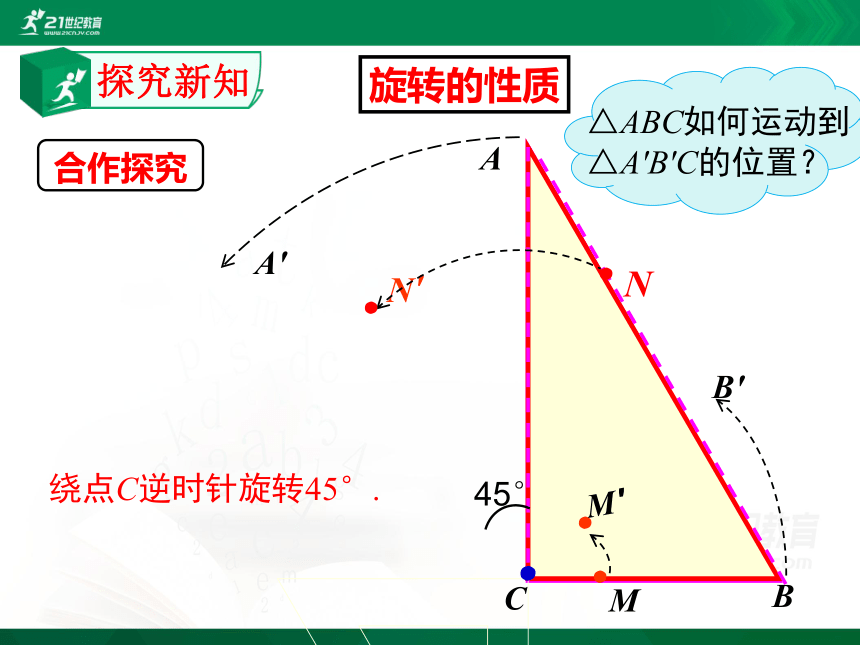
绕点C逆时针旋转45°.
△ABC如何运动到△A′B′C的位置?
合作探究
探究新知
旋转中心是点__________;
图中对应点有
;
图中对应线段有_____________________________________.
每对对应线段的长度有怎样的关系?
图中旋转角等于________.
C
点A与点A′,点B与点B′,点M与点M′,点N与点N′
线段CA与CA′、CB与CB′、AB与A′B′
45°
相等
根据上图填空.
B'
A'
C'
A
B
C
O
线段: AO=A'O ,BO=B'O ,CO =C'O
角:∠AOA'=∠BOB' =∠COC'
观察下图,你能找到相等的角和线段吗?
D
E
A
B
F
C
O
1. 对应点到旋转中心的距离相等;
2. 两组对应点分别与旋转中心的连线所成的角相等,
都等于旋转角;
3. 旋转中心是唯一不动的点.
旋转的性质
知识要点
A
B
O
例2 下图为 4×4 的正方形网格,每个小正方形的边长均为 1,将 △OAB 绕点 O 逆时针旋转 90°,你能画出
△OAB 旋转后的图形 △O′A′B′ 吗?
A′
B′
例3 如图,点E是正方形ABCD内一点,连接AE,BE,CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置,若AE=1,BE=2,CE=3,则∠BE′C=________度.
解析:连接EE′.
由旋转性质知BE=BE′,∠EBE′=90°,
∴∠BE'E=45°,
EE′
在△EE′C中,E′C=1,CE=3,
EE′
由勾股定理逆定理可知∠EE′C = 90°,
∴∠BE′C=∠BE′E+∠EE′C = 135°.
135
D
A
B
C
E
E′
例4 如图,将等腰△ABC绕顶点B逆时针方向旋转α°到△A1BC1的位置,AB与A1C1相交于点D,AC与A1C1,BC1分别交于点E,F.
(1)求证:△BA1D≌△BCF;
(2)当∠C=α°时,判定四边形A1BCE的形状,并说 明理由.
A
C
B
A1
C1
E
D
F
(1)证明:∵△ABC是等腰三角形,
∴AB=BC,∠A=∠C.
由旋转的性质,可得
A1B=AB=BC,∠A=∠A1=∠C,∠A1BD=∠CBF,
在△BA1D与△BCF中,
△BA1D≌△BCF.
A
C
B
A1
C1
E
D
F
(2)解:四边形A1BCE是菱形,理由如下:
∵∠FBC=∠C=α°,∠C=∠C1=α°,
∴∠FBC=∠C1,A1C1∥BC,
∴∠C1EC=∠C.
又∵△ABC,△A1BC1为等腰三角形,
∴∠A1=∠C1=∠C,∠A1=∠C1EC,
∴A1B∥CE,
∴四边形A1BCE是平行四边形,
又∵ A1B=BC,
∴□A1BCE是菱形.
A
C
B
A1
C1
E
D
F
旋转对称图形
活动 如图,在硬纸板上剪下两张如下图形,然后将它们叠放在一起,在其中心钉上一枚图钉,然后旋转上面的硬纸板,旋转一定角度后,它能与下面的硬纸板重合吗?
合作探究
探究新知
在平面内,一个图形绕着一个定点旋转一定的角度 θ (0°<θ<360°)后,能够与原图形重合,这样的图形叫做旋转对称图形,这个定点就是旋转中心.
知识要点
做一做
下图中不是旋转对称图形的是 ( )
B
例5 如图是一个标准的五角星,若将它绕旋转中心旋转一定角度后能与自身重合,则至少应将它旋转的度数是 ( )
A.60° B.72° C.90° D.144°
解析:如图,点O是五角星的中心,
则∠AOB=∠BOC=∠COD=∠DOE=
∠AOE,
∵它们都是旋转角,且它们的和为360°,
∴至少将它绕中心顺时针旋转360÷5=72°,
才能使正五角星旋转后与自身重合.故选B.
B
O
A
B
D
E
C
一个菱形绕它的两条对角线的交点旋转,使它和原来的菱形重合,那么旋转的角度至少是 ( )
A.360° B.270° C.180° D.90°
解析:∵菱形是中心对称图形,∴把菱形绕它的中心旋转,使它与原来的菱形重合,旋转角为180°的整数倍,∴旋转角至少是180°.故选C.
C
练一练
1. 下列事件中,属于旋转运动的是 ( )
A.小明向北走了4米
B.小朋友们在荡秋千时做的运动
C.电梯从1楼上升到12楼
D.一物体从高空坠下
B
课堂练习
2. 下列图形中,旋转对称图形的个数为 ( )
A.1 B.2 C.3 D.4
C
3. 要使下图中的图形旋转后与自身重合,至少应将它
绕中心按逆时针方向旋转的度数为 ( )
A.30°
B.60°
C.120°
D.180°
解析:图形可看作是正六边形被平分成六部分,故每部分被分成的角是60°,故旋转60°的整数倍就可以与自身重合.故选B.
B
4. △A′OB′是△AOB绕点O按逆时针方向旋转得到的.
已知∠AOB =20 °,∠ A′OB =24°,AB=3,OA=5,
则A′B′ = ,OA ′ = ,旋转角为 °.
3
5
44
5. 如图,正方形A′B′C′D′是由正方形ABCD按顺时针方向
旋转45°而成的.
(1)若AB=4,则S正方形A′B′C′D′ = ;
(2) ∠BAB′= ,∠B′AD= .
(3)若连接BB′,则∠ABB′= .
16
45°
45°
67.5°
A
B
C
D
E
6. 如图,将 Rt△ABC 绕点 A 按顺时针方向旋转一定
角度得 Rt△ADE,点 B 的对应点 D 恰好落在 BC
边上.若 AC = ,∠B = 60 °,则 CD 的长为 .
1
解析:∵Rt△ABC 中,
AC = ,∠B = 60 °,
∴ AB=1,BC=2.
由旋转得,AD=AB,
∴△ABD为等边三角形,∴BD=AB=1,
∴CD=BC-BD=2-1=1.
7. 在图中,将大写字母 A 绕它上侧的顶点按逆时针方
向旋转90°,作出旋转后的图案,同时作出字母 A
向左平移 5 个单位的图案.
A
C
B
E
D
C1
B1
D1
E1
A2
C2
B2
E2
D2
8. K 是正方形 ABCD 内一点,以 AK 为一边作正方形
AKLM,使 L、M 在 AK 的同旁,连接 BK 和 DM,
试用旋转的思想说明线段BK与DM的数量关系和位
置关系.
解:BK=DM,BK ⊥DM.
简要思路:由题意知,△ABK绕点 A逆时针旋转 90°得到△ADM,由旋转性质可知 BK=DM,BK ⊥DM.
A
B
C
D
K
L
M
定义
三要素:旋转中心、旋转方向和旋转角度
性质
①对应点到旋转中心的距离相等;
②两组对应点分别与旋转中心的连线所成
的角相等,都等于旋转角;
③旋转中心是唯一不动的点.
旋转对称图形
旋转的概念和性质
课堂小结
谢谢聆听
第1课时 旋转的概念和性质
24章 圆
2020-2021学年度沪科版九年级下册
1. 掌握旋转的有关概念及基本性质.(重点)
2. 能够根据旋转的基本性质解决实际问题和进行简单 作图.(难点)
学习目标
这些运动有什么共同的特点?
新课导入
旋转的概念
B
O
A
45
°
问题 观察下面的现象,它有什么特点?
观察与思考
探究新知
钟表的指针在不停地转动,从12时到4时,时针转动了______度.
120
把时针当成一个图形,那么它可以绕着中心固定点转动一定角度.
思考:怎样来定义这种图形变换?
风车风轮的每个叶片在风的吹动下转动到新的位置.
怎样来定义这种图形变换?
把叶片当成一个平面图形,那么它可以绕着平面内中心固定点转动一定角度.
在平面内,一个图形绕着一个定点,旋转一定的角度,得到另一个图形的变换,叫做旋转.
O
P′
P
旋转中心
旋转角
对
应
点
旋转的定义
这个定点叫做旋转中心.
转动的角称为旋转角.
图中的点 P 旋转后成为点 P',这两个点叫做对应点.
知识要点
若叶片 A 绕 O 顺时针旋转到叶片 B,则旋转中心是______,旋转角是_________,旋转角等于____,其中的对应点有_______、 _______、 _______、 _______、 _______、 _______ .
O
∠AOB
60°
F与A
A与B
B与C
C与D
D与E
E与F
填一填:
A
C
D
E
F
B
O
旋转中心
旋转角
旋转方向
必须明确
确定一次图形的旋转时,
注意:①旋转的范围是“平面内”,其中“旋转中心、
旋转方向、旋转角度”称为旋转的三要素;
②旋转变换同样属于全等变换.
归纳:
A.30°
B.45°
C.90°
D.135°
例1 如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点O按逆时针方向旋转到△COD的位置,则旋转的角度为 ( )
解析:对应点与旋转中心的连线的夹角,就是旋转角,由图可知,OB、OD是对应边,∠BOD是旋转角,所以,旋转角为90°.故选C.
C
C
D
A
B
O
例题讲解
旋转的性质
A
B
B′
A′
C
.
M′
M
.
.
.
.
45°
绕点C逆时针旋转45°.
△ABC如何运动到△A′B′C的位置?
合作探究
探究新知
旋转中心是点__________;
图中对应点有
;
图中对应线段有_____________________________________.
每对对应线段的长度有怎样的关系?
图中旋转角等于________.
C
点A与点A′,点B与点B′,点M与点M′,点N与点N′
线段CA与CA′、CB与CB′、AB与A′B′
45°
相等
根据上图填空.
B'
A'
C'
A
B
C
O
线段: AO=A'O ,BO=B'O ,CO =C'O
角:∠AOA'=∠BOB' =∠COC'
观察下图,你能找到相等的角和线段吗?
D
E
A
B
F
C
O
1. 对应点到旋转中心的距离相等;
2. 两组对应点分别与旋转中心的连线所成的角相等,
都等于旋转角;
3. 旋转中心是唯一不动的点.
旋转的性质
知识要点
A
B
O
例2 下图为 4×4 的正方形网格,每个小正方形的边长均为 1,将 △OAB 绕点 O 逆时针旋转 90°,你能画出
△OAB 旋转后的图形 △O′A′B′ 吗?
A′
B′
例3 如图,点E是正方形ABCD内一点,连接AE,BE,CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置,若AE=1,BE=2,CE=3,则∠BE′C=________度.
解析:连接EE′.
由旋转性质知BE=BE′,∠EBE′=90°,
∴∠BE'E=45°,
EE′
在△EE′C中,E′C=1,CE=3,
EE′
由勾股定理逆定理可知∠EE′C = 90°,
∴∠BE′C=∠BE′E+∠EE′C = 135°.
135
D
A
B
C
E
E′
例4 如图,将等腰△ABC绕顶点B逆时针方向旋转α°到△A1BC1的位置,AB与A1C1相交于点D,AC与A1C1,BC1分别交于点E,F.
(1)求证:△BA1D≌△BCF;
(2)当∠C=α°时,判定四边形A1BCE的形状,并说 明理由.
A
C
B
A1
C1
E
D
F
(1)证明:∵△ABC是等腰三角形,
∴AB=BC,∠A=∠C.
由旋转的性质,可得
A1B=AB=BC,∠A=∠A1=∠C,∠A1BD=∠CBF,
在△BA1D与△BCF中,
△BA1D≌△BCF.
A
C
B
A1
C1
E
D
F
(2)解:四边形A1BCE是菱形,理由如下:
∵∠FBC=∠C=α°,∠C=∠C1=α°,
∴∠FBC=∠C1,A1C1∥BC,
∴∠C1EC=∠C.
又∵△ABC,△A1BC1为等腰三角形,
∴∠A1=∠C1=∠C,∠A1=∠C1EC,
∴A1B∥CE,
∴四边形A1BCE是平行四边形,
又∵ A1B=BC,
∴□A1BCE是菱形.
A
C
B
A1
C1
E
D
F
旋转对称图形
活动 如图,在硬纸板上剪下两张如下图形,然后将它们叠放在一起,在其中心钉上一枚图钉,然后旋转上面的硬纸板,旋转一定角度后,它能与下面的硬纸板重合吗?
合作探究
探究新知
在平面内,一个图形绕着一个定点旋转一定的角度 θ (0°<θ<360°)后,能够与原图形重合,这样的图形叫做旋转对称图形,这个定点就是旋转中心.
知识要点
做一做
下图中不是旋转对称图形的是 ( )
B
例5 如图是一个标准的五角星,若将它绕旋转中心旋转一定角度后能与自身重合,则至少应将它旋转的度数是 ( )
A.60° B.72° C.90° D.144°
解析:如图,点O是五角星的中心,
则∠AOB=∠BOC=∠COD=∠DOE=
∠AOE,
∵它们都是旋转角,且它们的和为360°,
∴至少将它绕中心顺时针旋转360÷5=72°,
才能使正五角星旋转后与自身重合.故选B.
B
O
A
B
D
E
C
一个菱形绕它的两条对角线的交点旋转,使它和原来的菱形重合,那么旋转的角度至少是 ( )
A.360° B.270° C.180° D.90°
解析:∵菱形是中心对称图形,∴把菱形绕它的中心旋转,使它与原来的菱形重合,旋转角为180°的整数倍,∴旋转角至少是180°.故选C.
C
练一练
1. 下列事件中,属于旋转运动的是 ( )
A.小明向北走了4米
B.小朋友们在荡秋千时做的运动
C.电梯从1楼上升到12楼
D.一物体从高空坠下
B
课堂练习
2. 下列图形中,旋转对称图形的个数为 ( )
A.1 B.2 C.3 D.4
C
3. 要使下图中的图形旋转后与自身重合,至少应将它
绕中心按逆时针方向旋转的度数为 ( )
A.30°
B.60°
C.120°
D.180°
解析:图形可看作是正六边形被平分成六部分,故每部分被分成的角是60°,故旋转60°的整数倍就可以与自身重合.故选B.
B
4. △A′OB′是△AOB绕点O按逆时针方向旋转得到的.
已知∠AOB =20 °,∠ A′OB =24°,AB=3,OA=5,
则A′B′ = ,OA ′ = ,旋转角为 °.
3
5
44
5. 如图,正方形A′B′C′D′是由正方形ABCD按顺时针方向
旋转45°而成的.
(1)若AB=4,则S正方形A′B′C′D′ = ;
(2) ∠BAB′= ,∠B′AD= .
(3)若连接BB′,则∠ABB′= .
16
45°
45°
67.5°
A
B
C
D
E
6. 如图,将 Rt△ABC 绕点 A 按顺时针方向旋转一定
角度得 Rt△ADE,点 B 的对应点 D 恰好落在 BC
边上.若 AC = ,∠B = 60 °,则 CD 的长为 .
1
解析:∵Rt△ABC 中,
AC = ,∠B = 60 °,
∴ AB=1,BC=2.
由旋转得,AD=AB,
∴△ABD为等边三角形,∴BD=AB=1,
∴CD=BC-BD=2-1=1.
7. 在图中,将大写字母 A 绕它上侧的顶点按逆时针方
向旋转90°,作出旋转后的图案,同时作出字母 A
向左平移 5 个单位的图案.
A
C
B
E
D
C1
B1
D1
E1
A2
C2
B2
E2
D2
8. K 是正方形 ABCD 内一点,以 AK 为一边作正方形
AKLM,使 L、M 在 AK 的同旁,连接 BK 和 DM,
试用旋转的思想说明线段BK与DM的数量关系和位
置关系.
解:BK=DM,BK ⊥DM.
简要思路:由题意知,△ABK绕点 A逆时针旋转 90°得到△ADM,由旋转性质可知 BK=DM,BK ⊥DM.
A
B
C
D
K
L
M
定义
三要素:旋转中心、旋转方向和旋转角度
性质
①对应点到旋转中心的距离相等;
②两组对应点分别与旋转中心的连线所成
的角相等,都等于旋转角;
③旋转中心是唯一不动的点.
旋转对称图形
旋转的概念和性质
课堂小结
谢谢聆听
