24.1 旋转的应用(第3课时) 课件(共29张PPT)
文档属性
| 名称 | 24.1 旋转的应用(第3课时) 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-28 00:00:00 | ||
图片预览





文档简介
第3课时
旋转的应用
24.1 旋转
24章 圆
2020-2021学年度沪科版九年级下册
1. 理解并掌握旋转变化的特点,能够解决坐标平面内的旋转变换问题.(重点、难点)
2. 能够运用旋转、轴对称或平移进行简单的图案设计. (难点)
学习目标
你能找出图案中的全等图形吗?
这幅图案可看成是怎样制作的呢?
新课导入
运动美
★
★
★
★
★
★
★
★
★
★
★
★
组合美
坐标平面内的旋转变换
A
B
1
2
2
-1
-2
-2
x
y
O
1
-1
合作探究
C
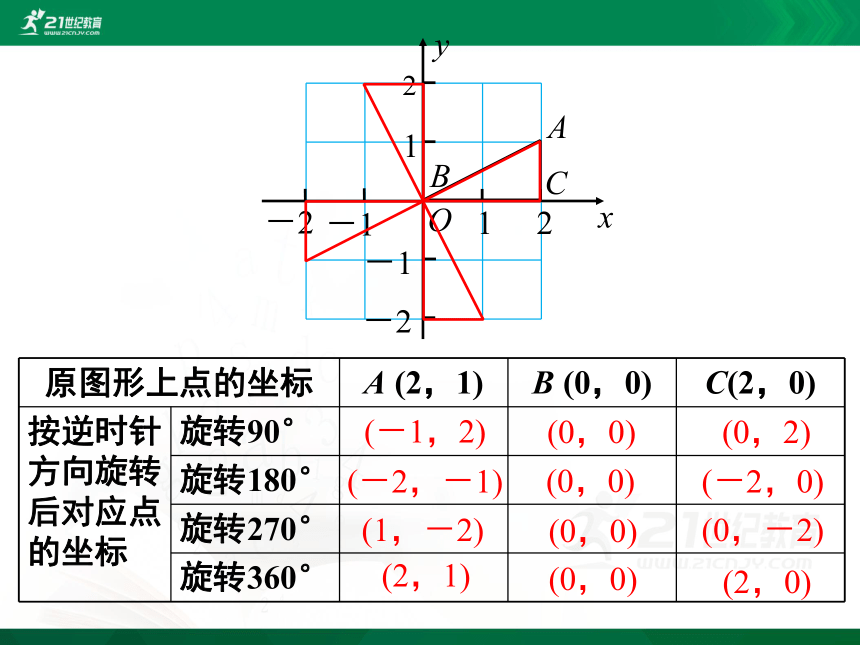
如图,△ABC 的顶点坐标分别是 A (2,1),B (0,0).
(1) 分别画出△ABC 以原点为旋转中心,逆时针旋转90°、180°、270°、360°而得到的△A′B′C′,并填写表格.
探究新知
A
B
1
2
2
-1
-2
-2
x
y
O
1
-1
C
原图形上点的坐标
A (2,1)
B (0,0)
C(2,0)
按逆时针方向旋转后对应点的坐标
旋转90°
旋转180°
旋转270°
旋转360°
(-1,2)
(-2,-1)
(1,-2)
(2,1)
(0,0)
(0,2)
(0,0)
(0,0)
(0,0)
(-2,0)
(0,-2)
(2,0)
(2) 分别比较点 A′ 与点 A、点 B′ 与点 B、点 C 与点 C′的坐标,能得到怎样的结论?
通过作图、分析能看到,把一个图形以坐标原点为旋转中心作几个特殊角度的旋转,可得如下结果:
原图形上任一点的坐标
以点O为旋转中心按逆时针方向旋转后对应点坐标
(x,y)
(-y,x)
(-x,-y)
(y,-x)
(x,y)
旋转90°
旋转180°
旋转270°
旋转360°
练一练
1. 如图,在方格纸上建立的平面直角坐标系中,将△ABO
绕点 O 按顺时针方向旋转 90°,得 △A′B′O,则点 A′的
坐标为 .
解析:根据网格结构找出点A、B旋转后的对应点A′、B′的位置,然后与点O顺次连接即可,再根据平面直角坐标系写出点A′的坐标.如图,点A′的坐标为(1,3).
(1,3)
2. 填空:
(1) 在平面直角坐标系中,点 P(2,-3) 关于原点对
称的点 P′ 的坐标是________.
(2) 点 M(3,-5) 绕原点旋转180°后到达的位置是
________.
(3)点P(2,n)与点Q(m,-3)关于原点对称,则(m+
n)2017=________.
解析:因为点 P(2,n) 与点 Q(m,-3) 关于原点对称,所以m=-2,n=3,则(m+n)2017=(-2+3)2017=1.
(-2,3)
1
(-3,5)
例1 如图,在平面直角坐标系中,点B的坐标是(1,0),若点 A 的坐标为(a,b),将线段BA绕点B顺时针旋转90°得到线段BA′,则点A′的坐标是 (b+1,-a+1) .
例题讲解
解析:过点 A 作 AC⊥x 轴,过点 A′ 作 A′D ⊥ x 轴,垂足分别为 C、D,显然
Rt △ABC ≌ Rt △BA′D. ∵点 A 的坐标为 (a,b),点 B 的坐标是 (1,0),∴OD=OB+BD=OB+AC=1+b,A′D=BC=OC-OB=a-1. ∵点 A′ 在第四象限,∴点A′的坐标是(b+1,-a+1).故答案为(b+1,-a+1).
动态图形的操作与图案设计
试说出构成下列图形的基本图形.
观察与思考
(1)
(2)
(3)
(4)
探究新知
基本图案
图案的形成过程
分析图案的形成过程
基本图案
图案的形成过程
分析图案的形成过程
归纳:图形的变换可以通过选择不同的变换方式得到,可能需要旋转、轴对称、平移等多种变换组合才能得到完美的图案.
例2 用四块如图(1)所示的正方形卡片拼成一个新的正方形,使拼成的图案是一个轴对称图形,请你在图(2)、图(3)、图(4)中各画出一种拼法(要求三种画法各不相同,且其中至少有一个既是轴对称图形,又是中心对称图形).
解:如图所示.(答案不唯一)
例3 如图,是一个4×4的正方形网格,每个小正方形的边长为1.请你在网格中以左上角的三角形为基本图形,通过平移、轴对称或旋转变换,设计一个精美图案,使其满足:①既是轴对称图形,又是以点O为对称中心的中心对称图形;②所作图案用阴影标识,且阴影部分面积为4.
分析:所给左上角的三角形的面积为 1×1÷2=0.5,故设计图案总共需要三角形 4÷0.5=8 (个).
解:答案不唯一,以下图案供参考.
1. 在下列某品牌T恤的四个洗涤说明图案的设计中,没
有运用旋转或轴对称知识的是 ( )
A B C D
C
课堂练习
3. 若点 A(m,-2),B(1,n)关于原点对称,则 m =___,
n =___ .
-1
2
2. 将点 P(2,-3) 绕原点逆时针旋转270°得到的点 P′
的坐标为 ( )
A. (-2,-3) B. (-3,2)
C. (-3,-2) D. (2,3)
C
4. 在平面直角坐标系 xOy 中,已知点 A(-3,4),将OA
绕坐标原点 O 逆时针旋转 90°至 OA′,则点 A′ 的坐
标是 .
(-4,-3)
5. 已知 a<0,则点 P(-a2,-a+1) 关于原点的对称点
P′ 在 .
解析:∵点 P(-a2,-a+1) 关于原点的对称点 P′ 的坐标为 (a2,a-1),a<0,∴a2>0,a-1<0,∴点P′ 在第四象限.
第四象限
6. 如图,在边长为 1 个单位长度的正方形方格纸中建立
平面直角坐标系,△ABC各顶点的坐标为A(-5,4),
B(-1,1),C(-5,1).
(1) 将△ABC绕着原点O顺时针旋转90°得到△A′B′C′,
请在图中画出△A′B′C′;
(2) 写出点A′的坐标.
A′
B
x
y
O
C
B′
C′
A
解:(1) 如图.
(2) A′点的坐
标为(4,5).
7. 如图是五个小正方形在3×3的正方形网格中拼成的图
形,请你移动其中一个小正方形,重新拼成一个图形,
使得所拼成的图形满足下列条件,并分别画在图①、
图②、图③中(只需各画一个,内部涂上阴影).
①是轴对称图形,但不是中心对称图形;
②是中心对称图形,但不是轴对称图形;
③既是轴对称图形,又是中心对称图形.
图①
图②
图③
8.试写出直线 y = 3x-5 关于原点对称的直线的函数关
系式.
解:y = 3x+5.
旋转的应用
特征
P (x,y)关于原点的对称点为P′(-x,-y).
作图
作出关于原点对称的图形,先求出对称点的坐标,再描点画图.
坐标平面内的旋转
变换
动态图形的操作与图案设计
分析图案设计
分清基本图形
知道形成过程
设计方法
利用图形变换
轴对称
平 移
旋 转
课堂小结
谢谢聆听
旋转的应用
24.1 旋转
24章 圆
2020-2021学年度沪科版九年级下册
1. 理解并掌握旋转变化的特点,能够解决坐标平面内的旋转变换问题.(重点、难点)
2. 能够运用旋转、轴对称或平移进行简单的图案设计. (难点)
学习目标
你能找出图案中的全等图形吗?
这幅图案可看成是怎样制作的呢?
新课导入
运动美
★
★
★
★
★
★
★
★
★
★
★
★
组合美
坐标平面内的旋转变换
A
B
1
2
2
-1
-2
-2
x
y
O
1
-1
合作探究
C
如图,△ABC 的顶点坐标分别是 A (2,1),B (0,0).
(1) 分别画出△ABC 以原点为旋转中心,逆时针旋转90°、180°、270°、360°而得到的△A′B′C′,并填写表格.
探究新知
A
B
1
2
2
-1
-2
-2
x
y
O
1
-1
C
原图形上点的坐标
A (2,1)
B (0,0)
C(2,0)
按逆时针方向旋转后对应点的坐标
旋转90°
旋转180°
旋转270°
旋转360°
(-1,2)
(-2,-1)
(1,-2)
(2,1)
(0,0)
(0,2)
(0,0)
(0,0)
(0,0)
(-2,0)
(0,-2)
(2,0)
(2) 分别比较点 A′ 与点 A、点 B′ 与点 B、点 C 与点 C′的坐标,能得到怎样的结论?
通过作图、分析能看到,把一个图形以坐标原点为旋转中心作几个特殊角度的旋转,可得如下结果:
原图形上任一点的坐标
以点O为旋转中心按逆时针方向旋转后对应点坐标
(x,y)
(-y,x)
(-x,-y)
(y,-x)
(x,y)
旋转90°
旋转180°
旋转270°
旋转360°
练一练
1. 如图,在方格纸上建立的平面直角坐标系中,将△ABO
绕点 O 按顺时针方向旋转 90°,得 △A′B′O,则点 A′的
坐标为 .
解析:根据网格结构找出点A、B旋转后的对应点A′、B′的位置,然后与点O顺次连接即可,再根据平面直角坐标系写出点A′的坐标.如图,点A′的坐标为(1,3).
(1,3)
2. 填空:
(1) 在平面直角坐标系中,点 P(2,-3) 关于原点对
称的点 P′ 的坐标是________.
(2) 点 M(3,-5) 绕原点旋转180°后到达的位置是
________.
(3)点P(2,n)与点Q(m,-3)关于原点对称,则(m+
n)2017=________.
解析:因为点 P(2,n) 与点 Q(m,-3) 关于原点对称,所以m=-2,n=3,则(m+n)2017=(-2+3)2017=1.
(-2,3)
1
(-3,5)
例1 如图,在平面直角坐标系中,点B的坐标是(1,0),若点 A 的坐标为(a,b),将线段BA绕点B顺时针旋转90°得到线段BA′,则点A′的坐标是 (b+1,-a+1) .
例题讲解
解析:过点 A 作 AC⊥x 轴,过点 A′ 作 A′D ⊥ x 轴,垂足分别为 C、D,显然
Rt △ABC ≌ Rt △BA′D. ∵点 A 的坐标为 (a,b),点 B 的坐标是 (1,0),∴OD=OB+BD=OB+AC=1+b,A′D=BC=OC-OB=a-1. ∵点 A′ 在第四象限,∴点A′的坐标是(b+1,-a+1).故答案为(b+1,-a+1).
动态图形的操作与图案设计
试说出构成下列图形的基本图形.
观察与思考
(1)
(2)
(3)
(4)
探究新知
基本图案
图案的形成过程
分析图案的形成过程
基本图案
图案的形成过程
分析图案的形成过程
归纳:图形的变换可以通过选择不同的变换方式得到,可能需要旋转、轴对称、平移等多种变换组合才能得到完美的图案.
例2 用四块如图(1)所示的正方形卡片拼成一个新的正方形,使拼成的图案是一个轴对称图形,请你在图(2)、图(3)、图(4)中各画出一种拼法(要求三种画法各不相同,且其中至少有一个既是轴对称图形,又是中心对称图形).
解:如图所示.(答案不唯一)
例3 如图,是一个4×4的正方形网格,每个小正方形的边长为1.请你在网格中以左上角的三角形为基本图形,通过平移、轴对称或旋转变换,设计一个精美图案,使其满足:①既是轴对称图形,又是以点O为对称中心的中心对称图形;②所作图案用阴影标识,且阴影部分面积为4.
分析:所给左上角的三角形的面积为 1×1÷2=0.5,故设计图案总共需要三角形 4÷0.5=8 (个).
解:答案不唯一,以下图案供参考.
1. 在下列某品牌T恤的四个洗涤说明图案的设计中,没
有运用旋转或轴对称知识的是 ( )
A B C D
C
课堂练习
3. 若点 A(m,-2),B(1,n)关于原点对称,则 m =___,
n =___ .
-1
2
2. 将点 P(2,-3) 绕原点逆时针旋转270°得到的点 P′
的坐标为 ( )
A. (-2,-3) B. (-3,2)
C. (-3,-2) D. (2,3)
C
4. 在平面直角坐标系 xOy 中,已知点 A(-3,4),将OA
绕坐标原点 O 逆时针旋转 90°至 OA′,则点 A′ 的坐
标是 .
(-4,-3)
5. 已知 a<0,则点 P(-a2,-a+1) 关于原点的对称点
P′ 在 .
解析:∵点 P(-a2,-a+1) 关于原点的对称点 P′ 的坐标为 (a2,a-1),a<0,∴a2>0,a-1<0,∴点P′ 在第四象限.
第四象限
6. 如图,在边长为 1 个单位长度的正方形方格纸中建立
平面直角坐标系,△ABC各顶点的坐标为A(-5,4),
B(-1,1),C(-5,1).
(1) 将△ABC绕着原点O顺时针旋转90°得到△A′B′C′,
请在图中画出△A′B′C′;
(2) 写出点A′的坐标.
A′
B
x
y
O
C
B′
C′
A
解:(1) 如图.
(2) A′点的坐
标为(4,5).
7. 如图是五个小正方形在3×3的正方形网格中拼成的图
形,请你移动其中一个小正方形,重新拼成一个图形,
使得所拼成的图形满足下列条件,并分别画在图①、
图②、图③中(只需各画一个,内部涂上阴影).
①是轴对称图形,但不是中心对称图形;
②是中心对称图形,但不是轴对称图形;
③既是轴对称图形,又是中心对称图形.
图①
图②
图③
8.试写出直线 y = 3x-5 关于原点对称的直线的函数关
系式.
解:y = 3x+5.
旋转的应用
特征
P (x,y)关于原点的对称点为P′(-x,-y).
作图
作出关于原点对称的图形,先求出对称点的坐标,再描点画图.
坐标平面内的旋转
变换
动态图形的操作与图案设计
分析图案设计
分清基本图形
知道形成过程
设计方法
利用图形变换
轴对称
平 移
旋 转
课堂小结
谢谢聆听
