24.2.4 圆的确定 课件(共29张PPT)
文档属性
| 名称 | 24.2.4 圆的确定 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-28 20:17:05 | ||
图片预览




文档简介
第4课时 圆的确定
24.2 圆的基本性质
24章 圆
2020-2021学年度沪科版九年级下册
1. 理解并掌握三点确定圆的条件并会应用. (重点)
2. 理解并掌握三角形的外接圆及外心的概念. (难点)
3. 了解反证法的证明思想.
学习目标
一位考古学家在长沙马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家画出这个碎片所在的整圆,以便于进行深入的研究吗?
要确定一个圆必须
满足几个条件?
新课导入
过不共线三点作圆
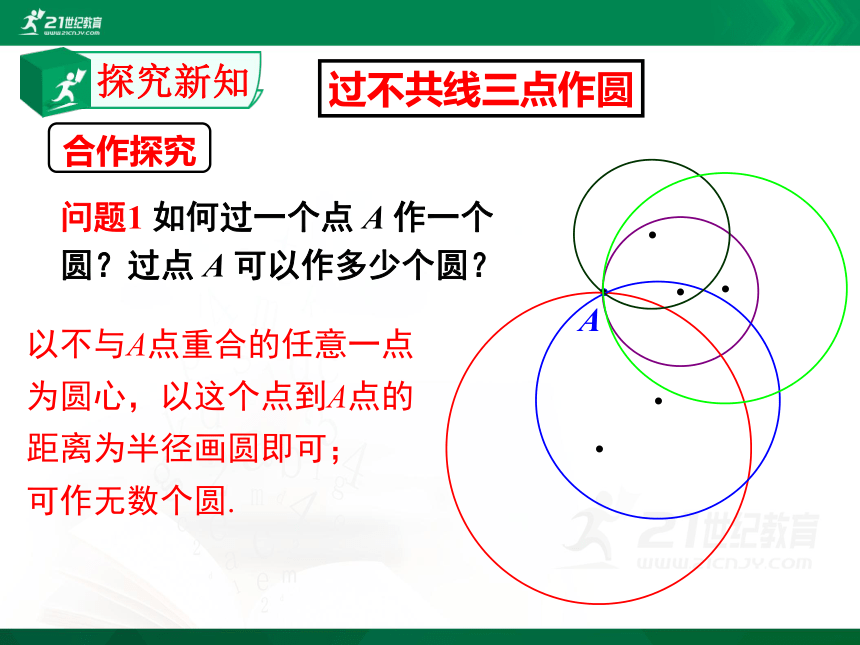
问题1 如何过一个点 A 作一个圆?过点 A 可以作多少个圆?
合作探究
·
·
·
·
·
以不与A点重合的任意一点为圆心,以这个点到A点的距离为半径画圆即可;
可作无数个圆.
A
探究新知
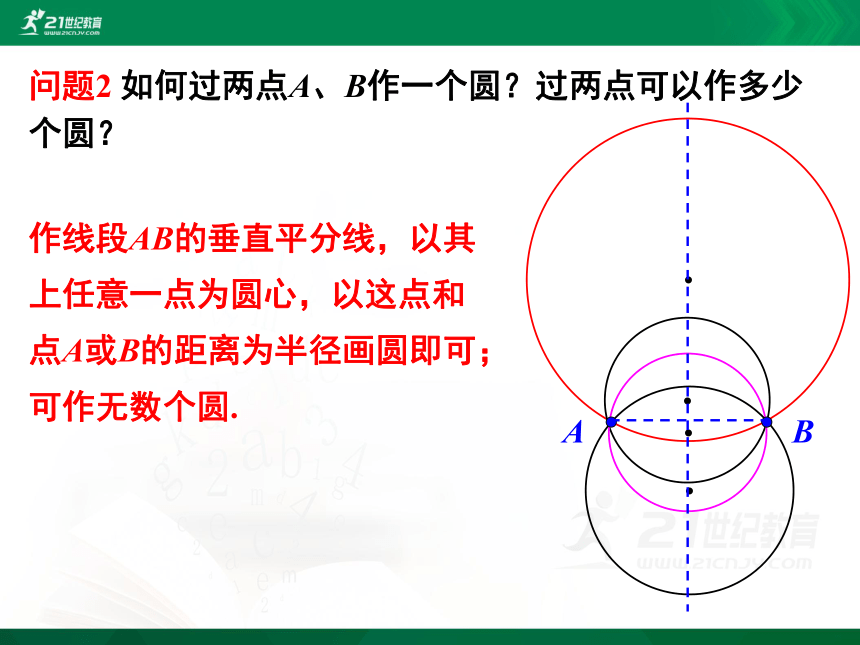
问题2 如何过两点A、B作一个圆?过两点可以作多少
个圆?
·
·
·
·
A
B
作线段AB的垂直平分线,以其上任意一点为圆心,以这点和点A或B的距离为半径画圆即可;
可作无数个圆.
问题3 过不在同一直线上的三点能不能确定一个圆?
A
B
C
D
E
G
F
O
经过B,C两点的圆的圆心在线段BC的垂直平分线上.
?经过A,B,C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.
经过A,B两点的圆的圆心在线段AB的垂直平分线上.
这个圆的圆心需要满足什么条件?
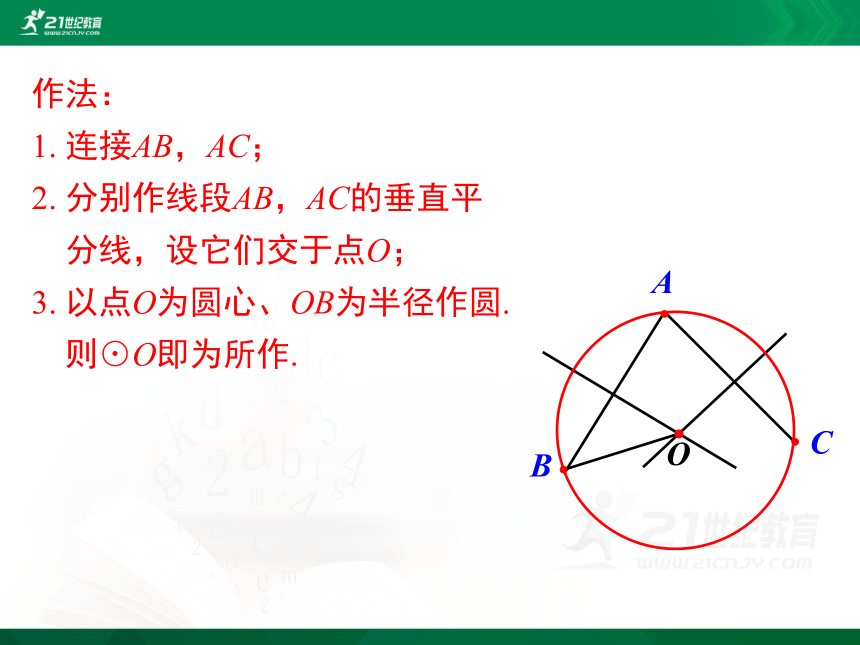
作法:
1. 连接AB,AC;
2. 分别作线段AB,AC的垂直平
分线,设它们交于点O;
3. 以点O为圆心、OB为半径作圆.
则⊙O即为所作.
O
A
B
C
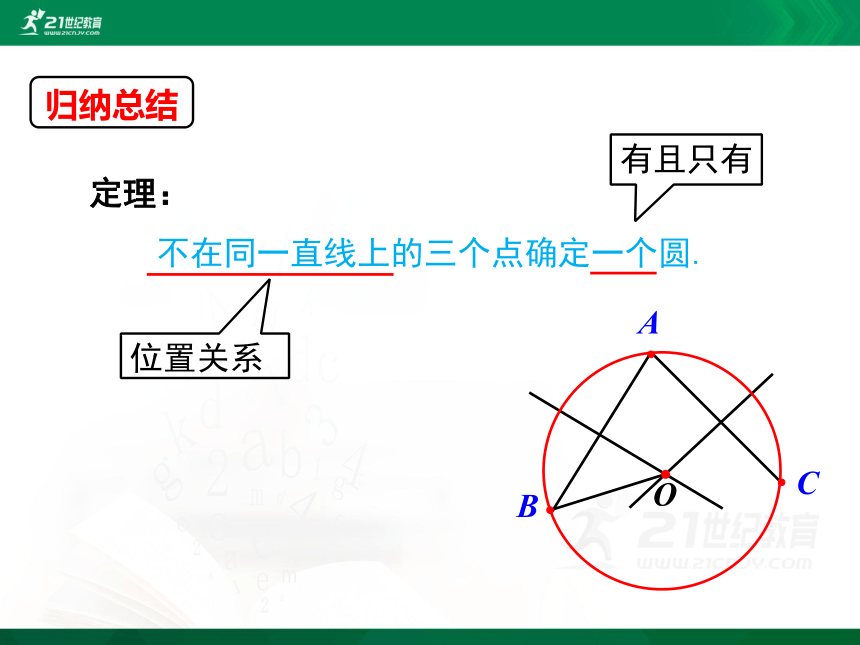
定理:
不在同一直线上的三个点确定一个圆.
有且只有
位置关系
归纳总结
O
A
B
C
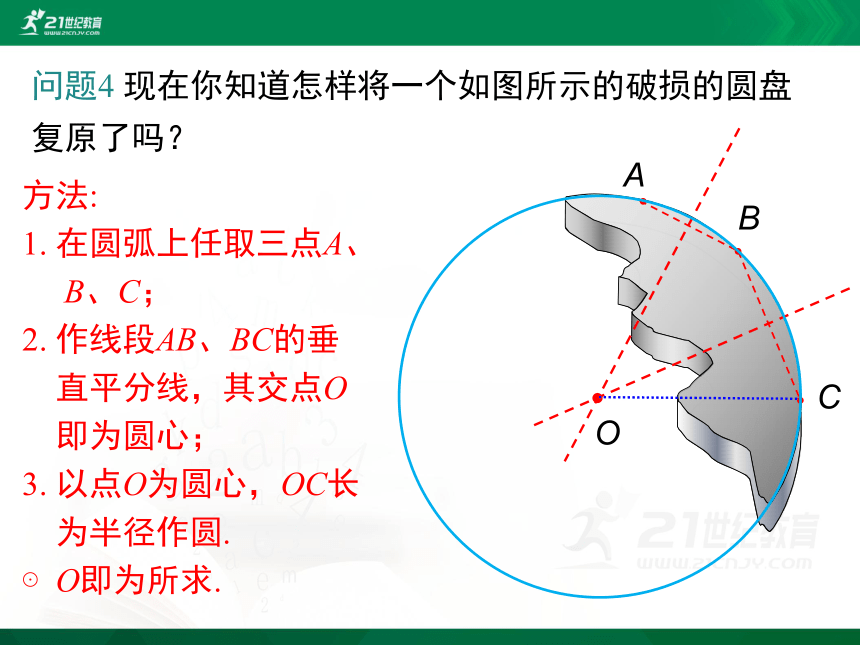
问题4 现在你知道怎样将一个如图所示的破损的圆盘复原了吗?
方法:
1. 在圆弧上任取三点A、
B、C;
2. 作线段AB、BC的垂
直平分线,其交点O
即为圆心;
3. 以点O为圆心,OC长
为半径作圆.
⊙O即为所求.
A
B
C
O
某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等.请问同学们这所中学建在哪个位置?你怎么确定这个位置呢?
●
●
●
B
A
C
练一练
根据前面学习的定理,若已知△ABC,我们可以用直尺与圆规作出过这个三角形三个顶点的圆.
A
B
C
O
三角形的外接圆及外心
概念学习
探究新知
这个三角形叫做圆的内接三角形.
经过三角形三个顶点的圆叫做三角形的外接圆,
外接圆的圆心叫做三角形的外心.
●O
A
B
C
三角形的外心到三角形的三个顶点距离相等.
判断:
(1) 任意的一个三角形一定有一个外接圆 ( )
(2) 任意一个圆有且只有一个内接三角形 ( )
(3) 经过三点一定可以确定一个圆 ( )
(4) 三角形的外心到三角形各顶点的距离相等 ( )
√
×
×
√
练一练
画一画:分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
锐角三角形的外心位于三角形内;
直角三角形的外心位于直角三角形斜边的中点;
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
例1 如图,△ABC的外接圆的圆心坐标是 .
解析:由图可知 △ABC 外接圆的圆心在 BC的垂直平分线上,即外接圆圆心在直线 y=-1 上,也在线段 AB的垂直平分线上,即外接圆圆心在直线 y = x+1 上,将上面两个式子联立,解得 x=-2,y=-1,则两线交点坐标即圆心坐标为(-2,-1).
(-2,-1)
例题讲解
例2 如图,在△ABC中,O是它的外心,BC=24cm,O到BC的距离是5cm,求△ABC的外接圆的半径.
解:连接OB,过点O作OD⊥BC,如图.
D
则OD = 5cm,
在Rt△OBD中,
即△ABC的外接圆的半径为13cm.
经过同一条直线上的三个点能作出一个圆吗?
A
B
C
反证法
观察与思考
l
探究新知
l1
l2
A
B
C
P
如图,假设经过直线l上的三点A、B、C可以作圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上.
这样,经过点P便有两条直线l1,l2都垂直于直线l,这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾,所以过同一条直线上的三点不能作圆.
l
上面的证明不是直接从题设推出结论,而是先假设命题结论不成立,然后经过推理,得出矛盾的结果,最后断言结论一定成立,这样的证明方法叫做反证法.
①反设:假设命题的结论不成立;
②推理:从这个假设出发,经过推理,得出矛盾;
③结论:由矛盾判定假设不成立,从而肯定命题的结
论成立.
知识要点
反证法的一般步骤
例3 已知:如图,直线AB∥CD,直线EF分别交AB,CD于点O1,O2.
求证:∠EO1B=∠EO2D.
A
B
C
D
E
F
O1
O2
证明:假设∠EO1B≠∠EO2D,过点O1作直线A'B',使∠EO1B'=∠EO2D,
∴A'B'∥CD.
这样,过点O1就有两条直线AB,A′B′平行于直线CD,这与“过直线外一点有且只有一条直线与这条直线平行”相矛盾,即∠EO1B≠∠EO2D的假设不成立.
∴∠EO1B=∠EO2D.
A'
B'
1.判断:
(1)经过三点一定可以作圆 ( )
(2)三角形的外心就是这个三角形两边垂直平分线的
交点 ( )
(3)三角形的外心到三边的距离相等 ( )
(4)等腰三角形的外心一定在这个三角形内 ( )
√
×
×
×
课堂练习
2. 小明不慎把家里的圆形玻璃打碎了,其中四块碎片
如图所示,为配到与原来大小一样的圆形玻璃,小
明带到商店去的一块玻璃碎片应该是 ( )
A.第①块 B.第④块
C.第③块 D.第②块
D
3. 如图,在5×5正方形网格中,一条圆弧经过A,B,C
三点,那么这条圆弧所在圆的圆心是 ( )
M
R
Q
A
B
C
P
A.点P B.点Q
C.点R D.点M
B
4. 如图,△ABC的外接圆的圆心坐标为 .
(6,2)
O
5. 已知:在 Rt△ABC 中,∠C=90°,AC=6,BC=8,
则它的外接圆半径= .
5
6. 如图,在△ABC中,点O在边AB上,且点O为△ABC
的外心,求∠ACB的度数.
解:∵点O为△ABC的外心,
∴OA=OB=OC,
∴∠OAC=∠OCA,∠OCB=∠OBC.
∵∠OAC+∠OCA+∠OCB+∠OBC=180°,
∴∠OCA+∠OCB=90°,
即∠ACB=90°.
7. 用反证法证明:一个圆只有一个圆心.
证明:假设⊙O有两个圆心O及O′,
在圆内任作一弦AB,设弦AB的中点为P,
连结OP,O′P,则OP⊥AB,O′P⊥AB,
过直线AB上一点P,同时有两条直线OP,O′P都垂直于AB,与垂线的性质矛盾,
故一个圆只有一个圆心.
圆的确定
圆的确定
三角形的外接圆
反证法
不在同一直线上的三个点确定一个圆
外接圆
外心
内接三角形
三角形外心的到三角形的三个顶点距离相等
课堂小结
谢谢聆听
24.2 圆的基本性质
24章 圆
2020-2021学年度沪科版九年级下册
1. 理解并掌握三点确定圆的条件并会应用. (重点)
2. 理解并掌握三角形的外接圆及外心的概念. (难点)
3. 了解反证法的证明思想.
学习目标
一位考古学家在长沙马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家画出这个碎片所在的整圆,以便于进行深入的研究吗?
要确定一个圆必须
满足几个条件?
新课导入
过不共线三点作圆
问题1 如何过一个点 A 作一个圆?过点 A 可以作多少个圆?
合作探究
·
·
·
·
·
以不与A点重合的任意一点为圆心,以这个点到A点的距离为半径画圆即可;
可作无数个圆.
A
探究新知
问题2 如何过两点A、B作一个圆?过两点可以作多少
个圆?
·
·
·
·
A
B
作线段AB的垂直平分线,以其上任意一点为圆心,以这点和点A或B的距离为半径画圆即可;
可作无数个圆.
问题3 过不在同一直线上的三点能不能确定一个圆?
A
B
C
D
E
G
F
O
经过B,C两点的圆的圆心在线段BC的垂直平分线上.
?经过A,B,C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.
经过A,B两点的圆的圆心在线段AB的垂直平分线上.
这个圆的圆心需要满足什么条件?
作法:
1. 连接AB,AC;
2. 分别作线段AB,AC的垂直平
分线,设它们交于点O;
3. 以点O为圆心、OB为半径作圆.
则⊙O即为所作.
O
A
B
C
定理:
不在同一直线上的三个点确定一个圆.
有且只有
位置关系
归纳总结
O
A
B
C
问题4 现在你知道怎样将一个如图所示的破损的圆盘复原了吗?
方法:
1. 在圆弧上任取三点A、
B、C;
2. 作线段AB、BC的垂
直平分线,其交点O
即为圆心;
3. 以点O为圆心,OC长
为半径作圆.
⊙O即为所求.
A
B
C
O
某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等.请问同学们这所中学建在哪个位置?你怎么确定这个位置呢?
●
●
●
B
A
C
练一练
根据前面学习的定理,若已知△ABC,我们可以用直尺与圆规作出过这个三角形三个顶点的圆.
A
B
C
O
三角形的外接圆及外心
概念学习
探究新知
这个三角形叫做圆的内接三角形.
经过三角形三个顶点的圆叫做三角形的外接圆,
外接圆的圆心叫做三角形的外心.
●O
A
B
C
三角形的外心到三角形的三个顶点距离相等.
判断:
(1) 任意的一个三角形一定有一个外接圆 ( )
(2) 任意一个圆有且只有一个内接三角形 ( )
(3) 经过三点一定可以确定一个圆 ( )
(4) 三角形的外心到三角形各顶点的距离相等 ( )
√
×
×
√
练一练
画一画:分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
锐角三角形的外心位于三角形内;
直角三角形的外心位于直角三角形斜边的中点;
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
例1 如图,△ABC的外接圆的圆心坐标是 .
解析:由图可知 △ABC 外接圆的圆心在 BC的垂直平分线上,即外接圆圆心在直线 y=-1 上,也在线段 AB的垂直平分线上,即外接圆圆心在直线 y = x+1 上,将上面两个式子联立,解得 x=-2,y=-1,则两线交点坐标即圆心坐标为(-2,-1).
(-2,-1)
例题讲解
例2 如图,在△ABC中,O是它的外心,BC=24cm,O到BC的距离是5cm,求△ABC的外接圆的半径.
解:连接OB,过点O作OD⊥BC,如图.
D
则OD = 5cm,
在Rt△OBD中,
即△ABC的外接圆的半径为13cm.
经过同一条直线上的三个点能作出一个圆吗?
A
B
C
反证法
观察与思考
l
探究新知
l1
l2
A
B
C
P
如图,假设经过直线l上的三点A、B、C可以作圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上.
这样,经过点P便有两条直线l1,l2都垂直于直线l,这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾,所以过同一条直线上的三点不能作圆.
l
上面的证明不是直接从题设推出结论,而是先假设命题结论不成立,然后经过推理,得出矛盾的结果,最后断言结论一定成立,这样的证明方法叫做反证法.
①反设:假设命题的结论不成立;
②推理:从这个假设出发,经过推理,得出矛盾;
③结论:由矛盾判定假设不成立,从而肯定命题的结
论成立.
知识要点
反证法的一般步骤
例3 已知:如图,直线AB∥CD,直线EF分别交AB,CD于点O1,O2.
求证:∠EO1B=∠EO2D.
A
B
C
D
E
F
O1
O2
证明:假设∠EO1B≠∠EO2D,过点O1作直线A'B',使∠EO1B'=∠EO2D,
∴A'B'∥CD.
这样,过点O1就有两条直线AB,A′B′平行于直线CD,这与“过直线外一点有且只有一条直线与这条直线平行”相矛盾,即∠EO1B≠∠EO2D的假设不成立.
∴∠EO1B=∠EO2D.
A'
B'
1.判断:
(1)经过三点一定可以作圆 ( )
(2)三角形的外心就是这个三角形两边垂直平分线的
交点 ( )
(3)三角形的外心到三边的距离相等 ( )
(4)等腰三角形的外心一定在这个三角形内 ( )
√
×
×
×
课堂练习
2. 小明不慎把家里的圆形玻璃打碎了,其中四块碎片
如图所示,为配到与原来大小一样的圆形玻璃,小
明带到商店去的一块玻璃碎片应该是 ( )
A.第①块 B.第④块
C.第③块 D.第②块
D
3. 如图,在5×5正方形网格中,一条圆弧经过A,B,C
三点,那么这条圆弧所在圆的圆心是 ( )
M
R
Q
A
B
C
P
A.点P B.点Q
C.点R D.点M
B
4. 如图,△ABC的外接圆的圆心坐标为 .
(6,2)
O
5. 已知:在 Rt△ABC 中,∠C=90°,AC=6,BC=8,
则它的外接圆半径= .
5
6. 如图,在△ABC中,点O在边AB上,且点O为△ABC
的外心,求∠ACB的度数.
解:∵点O为△ABC的外心,
∴OA=OB=OC,
∴∠OAC=∠OCA,∠OCB=∠OBC.
∵∠OAC+∠OCA+∠OCB+∠OBC=180°,
∴∠OCA+∠OCB=90°,
即∠ACB=90°.
7. 用反证法证明:一个圆只有一个圆心.
证明:假设⊙O有两个圆心O及O′,
在圆内任作一弦AB,设弦AB的中点为P,
连结OP,O′P,则OP⊥AB,O′P⊥AB,
过直线AB上一点P,同时有两条直线OP,O′P都垂直于AB,与垂线的性质矛盾,
故一个圆只有一个圆心.
圆的确定
圆的确定
三角形的外接圆
反证法
不在同一直线上的三个点确定一个圆
外接圆
外心
内接三角形
三角形外心的到三角形的三个顶点距离相等
课堂小结
谢谢聆听
