24.4.1直线与圆的位置关系 课件(共27张PPT)
文档属性
| 名称 | 24.4.1直线与圆的位置关系 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-28 00:00:00 | ||
图片预览



文档简介
24.4 直线与圆的位置关系
第1课时
直线与圆的位置关系
24章 圆
2020-2021学年度沪科版九年级下册
1. 理解直线与圆有相交、相切、相离三种位置关系.
2. 能根据圆心到直线的距离 d 和圆的半径 r 之间的数量关系,判断出直线与圆的位置关系. (重点)
学习目标
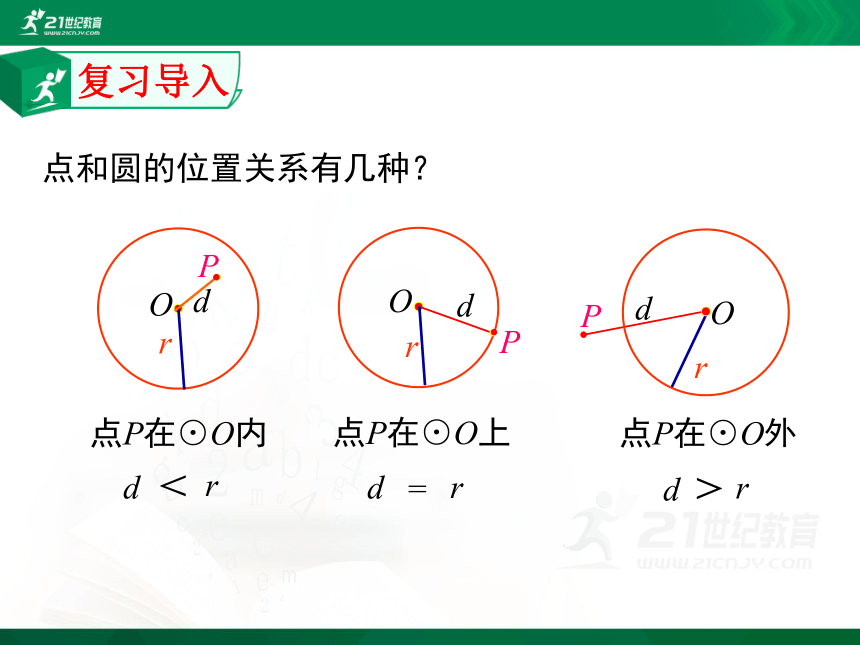
点和圆的位置关系有几种?
点P在⊙O内
r
P
d
d
<
r
P
r
d
点P在⊙O上
d
r
=
P
r
d
点P在⊙O外
d
>
r
O
O
O
复习导入
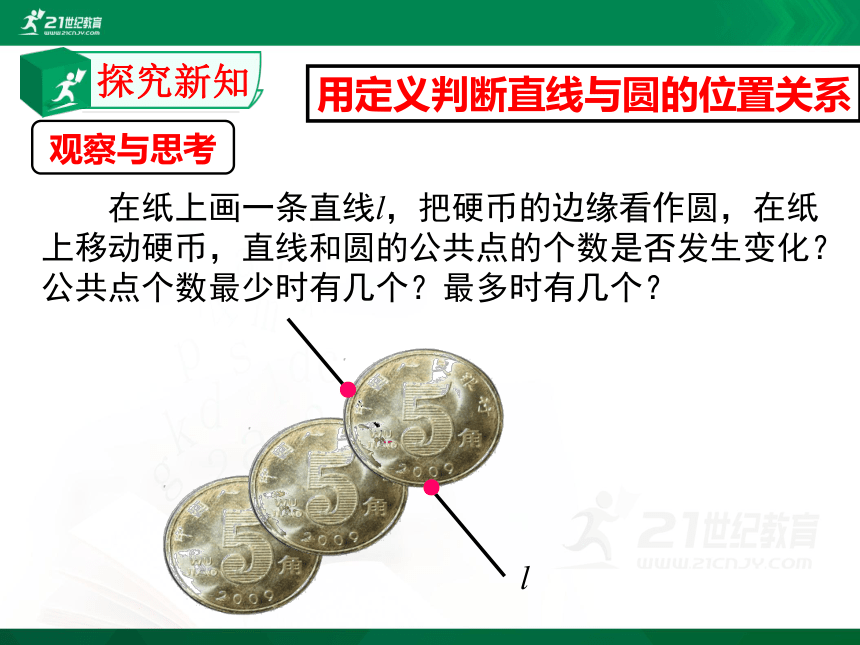
用定义判断直线与圆的位置关系
在纸上画一条直线l,把硬币的边缘看作圆,在纸上移动硬币,直线和圆的公共点的个数是否发生变化?公共点个数最少时有几个?最多时有几个?
●
●
●
l
观察与思考
探究新知
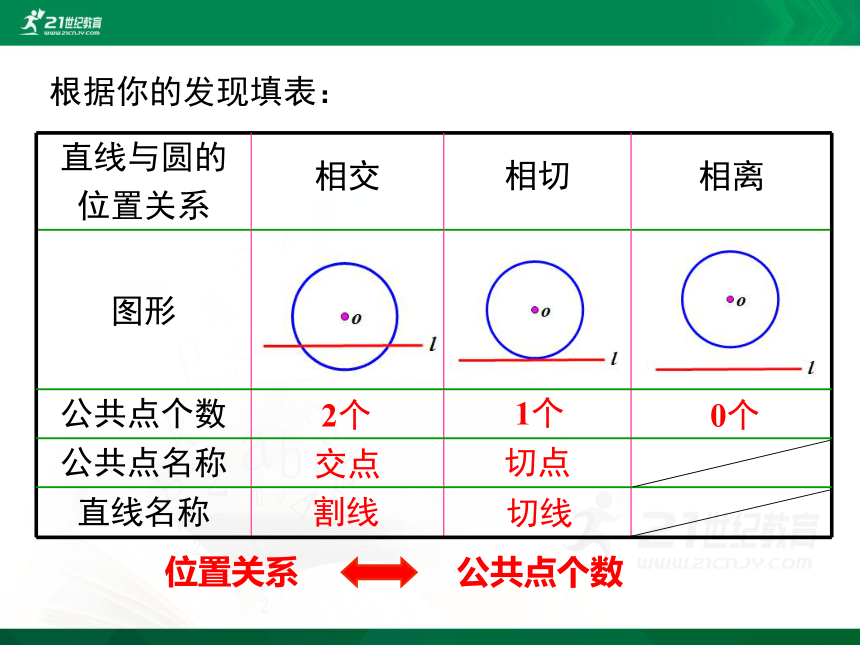
直线与圆的
位置关系
图形
公共点个数
公共点名称
直线名称
2个
交点
1个
切点
切线
0个
相离
相切
相交
位置关系
公共点个数
根据你的发现填表:
割线
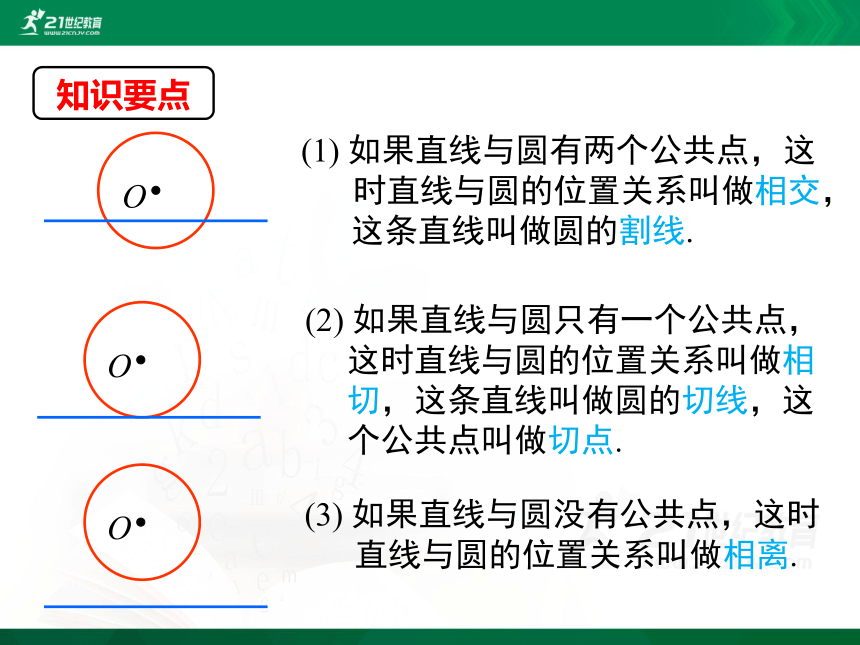
知识要点
(2) 如果直线与圆只有一个公共点,
这时直线与圆的位置关系叫做相
切,这条直线叫做圆的切线,这
个公共点叫做切点.
(1) 如果直线与圆有两个公共点,这
时直线与圆的位置关系叫做相交,
这条直线叫做圆的割线.
(3) 如果直线与圆没有公共点,这时
直线与圆的位置关系叫做相离.
O
O
O
1. 直线与圆最多有两个公共点.
2. 若直线与圆相交,则直线上的点都在圆上.
3. 若A是⊙O上一点,则直线AB与⊙O相切.
4. 若C为⊙O外一点,则过点C的直线与⊙O相交
或相离.
5. 直线a 和⊙O有公共点,则直线a与⊙O相交.
判断:
√
×
×
×
×
练一练
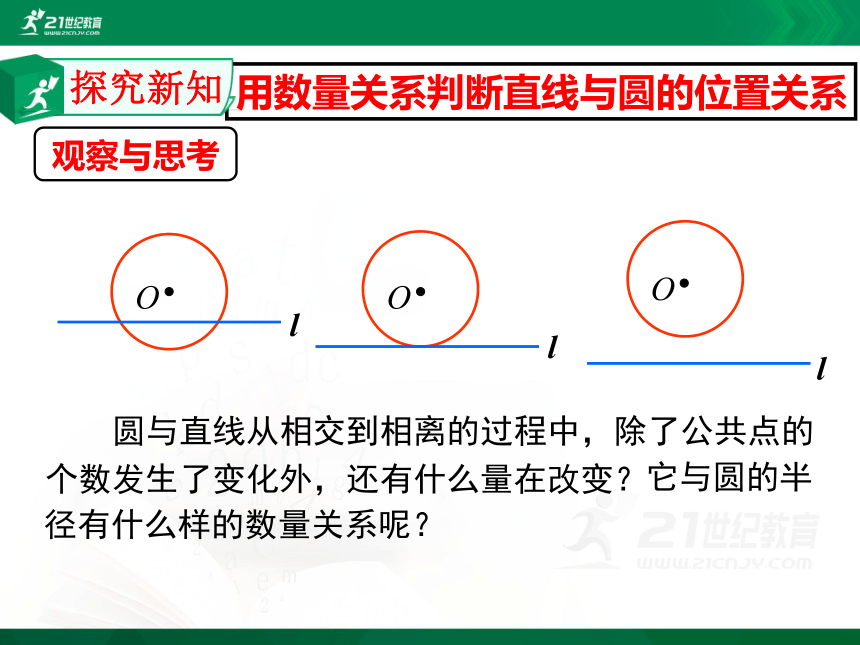
圆与直线从相交到相离的过程中,除了公共点的个数发生了变化外,还有什么量在改变?
用数量关系判断直线与圆的位置关系
观察与思考
它与圆的半径有什么样的数量关系呢?
O
O
O
l
l
l
探究新知
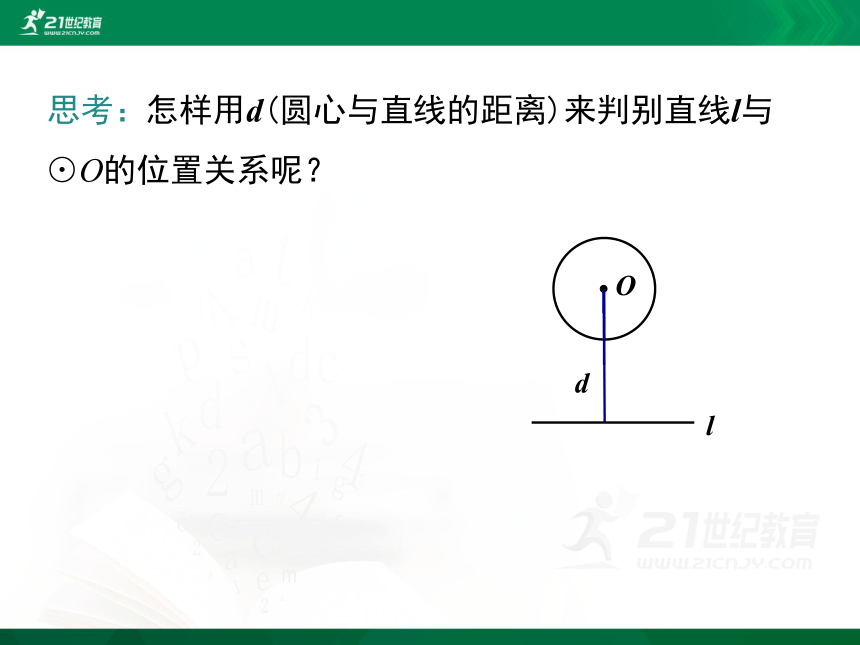
怎样用d(圆心与直线的距离)来判别直线l与⊙O的位置关系呢?
O
d
思考:
l
合作探究
直线和圆相交
d< r
直线和圆相切
d= r
直线和圆相离
d> r
r
d
r
d
r
d
位置关系
数量关系
用圆心 O 到直线l的距离 d 与圆的半径 r 的关系来判断直线与圆的位置关系:
o
o
o
知识要点
l
l
l
1. 已知圆的半径为6cm,设直线和圆心的距离为d :
(3) 若d=8cm,则直线与圆______,直线与圆有____个
公共点.
(2) 若d =6cm,则直线与圆______,直线与圆有____个
公共点;
(1) 若d =4cm,则直线与圆 ,直线与圆有____个
公共点;
相交
相切
相离
2
1
0
练一练
(3) 若AB和⊙O相交,则 .
2. 已知⊙O的半径为5cm,圆心O与直线AB的距离为d,
根据条件填写d的取值范围:
(1) 若AB和⊙O相离,则 ;
(2) 若AB和⊙O相切,则 ;
d > 5cm
d = 5cm
0 cm ≤ d < 5 cm
例1 如图,Rt△ABC的斜边AB=10cm,∠A=30°.
(1) 以点C为圆心,当半径为多少时,AB与☉C相切?
A
C
B
解: 过点C作边AB上的高CD.
D
∵∠A=30°,AB=10cm,
在Rt△BCD中,有
当半径为 时,AB与☉C相切.
∴∠B=60°,
例题讲解
(2) 以点C为圆心、半径 r 分别为 4cm 和 5cm 作两个圆,
这两个圆与斜边AB分别有怎样的位置关系?
A
C
B
D
当r =4cm时,d>r,⊙C与AB相离;
当r =5cm时,d<r,⊙C与AB相交.
解:由 (1) 可知圆心 C 到 AB 的距离
B
C
A
4
3
1. 在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以
C为圆心,r为半径的圆与AB有怎样的位置关系?
(1) r =2cm;(2) r =2.4cm;(3) r =3cm.
D
练一练
解:过C作CD⊥AB,垂足为D.
在△ABC中,
AB =
5.
根据三角形的面积公式有
∴
即圆心 C 到 AB 的距离 d = 2.4 cm.
∴ (1) 当r =2cm时,
有d >r,
因此,⊙C和AB相离.
(2) 当r =2.4cm时,有d = r,
因此,⊙C和AB相切.
(3) 当r=3cm时,有d < r,
因此,⊙C和AB相交.
A
B
C
A
D
4
5
3
2. Rt△ABC,∠C=90°,AC=3cm,BC=4cm,以C为
圆心画圆.
(1) 当半径r为何值时,⊙C与线段AB有一个公共点?
(2) 当半径r为何值时,⊙C与线段AB有两个公共点?
(3) 当半径r为何值时,⊙C与线段AB没有公共点?
(3) 当0cm<r<2.4cm或r>4cm时,⊙C与
线段AB没有公共点.
解:(1) 当r = 2.4cm或 3cm ≤ r<4cm时,
⊙C与线段AB有一个公共点.
(2) 当2.4cm<r≤3cm 时,⊙C与线段AB有两个公共点.
例2 如图,在平面直角坐标系中,⊙A 与 y 轴相切于原点 O,平行于 x 轴的直线交 ⊙A 于 M、N 两点.若点 M的坐标是 (-4,-2),则点 N 的坐标为 ( )
A.(-1,-2) B.(1,2)
C.(-1.5,-2) D.(1.5,-2)
解析:过点A作AQ⊥MN于点Q,连接AN,设半径为r,由垂径定理有MQ=NQ,所以AQ=2,AN=r,NQ=4-r,利用勾股定理得r2=4+(4-r)2,解得r=2.5,可以求出NQ=1.5,所以N点坐标为(-1,-2).故选A.
A
.O
.O
.O
.O
.O
1. 看图判断直线l与☉O的位置关系?
相离
相交
相切
相交
?
相交
l
l
l
l
l
课堂练习
2. 直线和圆相交,圆的半径为r,且圆心到直线的距离
为5,则有 ( )
A. r < 5 B. r > 5 C. r = 5 D. r ≥ 5
3. ☉O的半径为5,直线l上的一点P到圆心O的距离是5,
则直线 l 与☉O的位置关系是 ( )
A. 相交或相切 B. 相交或相离
C. 相切或相离 D. 上三种情况都有可能
B
A
解析:分两种情况讨论:(1)OP⊥直线l,则圆心到直线l的距离为5,此时直线l与⊙O相切;(2)若OP与直线l不垂直,则圆心到直线的距离小于5,此时直线l与⊙O相交.所以本题选A.
5. ☉O的最大弦长为 8,若圆心 O 到直线l的距离为d =
5,则直线l与☉O .
相离
4. 已知圆的半径等于 5,直线 l 与圆没有交点,则圆心
到直线 l 的距离 d 的取值范围是________.
d >5
6. 如图,∠ABC=80°,O为射线BC上一点,以点O为
圆心, OB长为半径作 ⊙O,要使射线BA与⊙O相
切,应将射线BA绕点B按顺时针方向旋转 ( )
A.40°或80°
B.50°或100°
C.50°或110°
D.60°或120°
C
7. 如图,M是OB上的一点,且OM = 5 cm,以M为圆心,
半径 r = 2.5cm 作⊙M. 试问:过 O 的射线 OA 与 OB
(OA 在 OB的上方)所夹的锐角α取什么值时射线OA
与⊙M (1)相离;(2)相切;(3)相交.
O
B
A
M
5
α
解:(1)30°<∠α<90°.
(2)∠α = 30°.
(3)∠α<30°.
8. 已知⊙O的半径为R,点O到直线m的距离为d,R、d
是方程 x2-2x+a=0 的两根,当直线m与⊙O相切时,
求a的值.
解:∵直线 m 与⊙O相切,
∴d =R,即方程 x2-2x+a=0 有两个相等的根,
∴Δ=4-4a=0,∴a=1.
直线与圆的位置关系
定义
性质
判定
相离
相切
相交
公共点的个数
d与r的数量关系
定义法
性质法
特别提醒:若图中没有d要先作出该垂线段
相离:0个
相切:1个
相交:2个
相离:d>r
相切:d=r
相交:d0个:相离;1个:相切;2个:相交
d>r:相离
d=r:相切
d课堂小结
谢谢聆听
第1课时
直线与圆的位置关系
24章 圆
2020-2021学年度沪科版九年级下册
1. 理解直线与圆有相交、相切、相离三种位置关系.
2. 能根据圆心到直线的距离 d 和圆的半径 r 之间的数量关系,判断出直线与圆的位置关系. (重点)
学习目标
点和圆的位置关系有几种?
点P在⊙O内
r
P
d
d
<
r
P
r
d
点P在⊙O上
d
r
=
P
r
d
点P在⊙O外
d
>
r
O
O
O
复习导入
用定义判断直线与圆的位置关系
在纸上画一条直线l,把硬币的边缘看作圆,在纸上移动硬币,直线和圆的公共点的个数是否发生变化?公共点个数最少时有几个?最多时有几个?
●
●
●
l
观察与思考
探究新知
直线与圆的
位置关系
图形
公共点个数
公共点名称
直线名称
2个
交点
1个
切点
切线
0个
相离
相切
相交
位置关系
公共点个数
根据你的发现填表:
割线
知识要点
(2) 如果直线与圆只有一个公共点,
这时直线与圆的位置关系叫做相
切,这条直线叫做圆的切线,这
个公共点叫做切点.
(1) 如果直线与圆有两个公共点,这
时直线与圆的位置关系叫做相交,
这条直线叫做圆的割线.
(3) 如果直线与圆没有公共点,这时
直线与圆的位置关系叫做相离.
O
O
O
1. 直线与圆最多有两个公共点.
2. 若直线与圆相交,则直线上的点都在圆上.
3. 若A是⊙O上一点,则直线AB与⊙O相切.
4. 若C为⊙O外一点,则过点C的直线与⊙O相交
或相离.
5. 直线a 和⊙O有公共点,则直线a与⊙O相交.
判断:
√
×
×
×
×
练一练
圆与直线从相交到相离的过程中,除了公共点的个数发生了变化外,还有什么量在改变?
用数量关系判断直线与圆的位置关系
观察与思考
它与圆的半径有什么样的数量关系呢?
O
O
O
l
l
l
探究新知
怎样用d(圆心与直线的距离)来判别直线l与⊙O的位置关系呢?
O
d
思考:
l
合作探究
直线和圆相交
d< r
直线和圆相切
d= r
直线和圆相离
d> r
r
d
r
d
r
d
位置关系
数量关系
用圆心 O 到直线l的距离 d 与圆的半径 r 的关系来判断直线与圆的位置关系:
o
o
o
知识要点
l
l
l
1. 已知圆的半径为6cm,设直线和圆心的距离为d :
(3) 若d=8cm,则直线与圆______,直线与圆有____个
公共点.
(2) 若d =6cm,则直线与圆______,直线与圆有____个
公共点;
(1) 若d =4cm,则直线与圆 ,直线与圆有____个
公共点;
相交
相切
相离
2
1
0
练一练
(3) 若AB和⊙O相交,则 .
2. 已知⊙O的半径为5cm,圆心O与直线AB的距离为d,
根据条件填写d的取值范围:
(1) 若AB和⊙O相离,则 ;
(2) 若AB和⊙O相切,则 ;
d > 5cm
d = 5cm
0 cm ≤ d < 5 cm
例1 如图,Rt△ABC的斜边AB=10cm,∠A=30°.
(1) 以点C为圆心,当半径为多少时,AB与☉C相切?
A
C
B
解: 过点C作边AB上的高CD.
D
∵∠A=30°,AB=10cm,
在Rt△BCD中,有
当半径为 时,AB与☉C相切.
∴∠B=60°,
例题讲解
(2) 以点C为圆心、半径 r 分别为 4cm 和 5cm 作两个圆,
这两个圆与斜边AB分别有怎样的位置关系?
A
C
B
D
当r =4cm时,d>r,⊙C与AB相离;
当r =5cm时,d<r,⊙C与AB相交.
解:由 (1) 可知圆心 C 到 AB 的距离
B
C
A
4
3
1. 在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以
C为圆心,r为半径的圆与AB有怎样的位置关系?
(1) r =2cm;(2) r =2.4cm;(3) r =3cm.
D
练一练
解:过C作CD⊥AB,垂足为D.
在△ABC中,
AB =
5.
根据三角形的面积公式有
∴
即圆心 C 到 AB 的距离 d = 2.4 cm.
∴ (1) 当r =2cm时,
有d >r,
因此,⊙C和AB相离.
(2) 当r =2.4cm时,有d = r,
因此,⊙C和AB相切.
(3) 当r=3cm时,有d < r,
因此,⊙C和AB相交.
A
B
C
A
D
4
5
3
2. Rt△ABC,∠C=90°,AC=3cm,BC=4cm,以C为
圆心画圆.
(1) 当半径r为何值时,⊙C与线段AB有一个公共点?
(2) 当半径r为何值时,⊙C与线段AB有两个公共点?
(3) 当半径r为何值时,⊙C与线段AB没有公共点?
(3) 当0cm<r<2.4cm或r>4cm时,⊙C与
线段AB没有公共点.
解:(1) 当r = 2.4cm或 3cm ≤ r<4cm时,
⊙C与线段AB有一个公共点.
(2) 当2.4cm<r≤3cm 时,⊙C与线段AB有两个公共点.
例2 如图,在平面直角坐标系中,⊙A 与 y 轴相切于原点 O,平行于 x 轴的直线交 ⊙A 于 M、N 两点.若点 M的坐标是 (-4,-2),则点 N 的坐标为 ( )
A.(-1,-2) B.(1,2)
C.(-1.5,-2) D.(1.5,-2)
解析:过点A作AQ⊥MN于点Q,连接AN,设半径为r,由垂径定理有MQ=NQ,所以AQ=2,AN=r,NQ=4-r,利用勾股定理得r2=4+(4-r)2,解得r=2.5,可以求出NQ=1.5,所以N点坐标为(-1,-2).故选A.
A
.O
.O
.O
.O
.O
1. 看图判断直线l与☉O的位置关系?
相离
相交
相切
相交
?
相交
l
l
l
l
l
课堂练习
2. 直线和圆相交,圆的半径为r,且圆心到直线的距离
为5,则有 ( )
A. r < 5 B. r > 5 C. r = 5 D. r ≥ 5
3. ☉O的半径为5,直线l上的一点P到圆心O的距离是5,
则直线 l 与☉O的位置关系是 ( )
A. 相交或相切 B. 相交或相离
C. 相切或相离 D. 上三种情况都有可能
B
A
解析:分两种情况讨论:(1)OP⊥直线l,则圆心到直线l的距离为5,此时直线l与⊙O相切;(2)若OP与直线l不垂直,则圆心到直线的距离小于5,此时直线l与⊙O相交.所以本题选A.
5. ☉O的最大弦长为 8,若圆心 O 到直线l的距离为d =
5,则直线l与☉O .
相离
4. 已知圆的半径等于 5,直线 l 与圆没有交点,则圆心
到直线 l 的距离 d 的取值范围是________.
d >5
6. 如图,∠ABC=80°,O为射线BC上一点,以点O为
圆心, OB长为半径作 ⊙O,要使射线BA与⊙O相
切,应将射线BA绕点B按顺时针方向旋转 ( )
A.40°或80°
B.50°或100°
C.50°或110°
D.60°或120°
C
7. 如图,M是OB上的一点,且OM = 5 cm,以M为圆心,
半径 r = 2.5cm 作⊙M. 试问:过 O 的射线 OA 与 OB
(OA 在 OB的上方)所夹的锐角α取什么值时射线OA
与⊙M (1)相离;(2)相切;(3)相交.
O
B
A
M
5
α
解:(1)30°<∠α<90°.
(2)∠α = 30°.
(3)∠α<30°.
8. 已知⊙O的半径为R,点O到直线m的距离为d,R、d
是方程 x2-2x+a=0 的两根,当直线m与⊙O相切时,
求a的值.
解:∵直线 m 与⊙O相切,
∴d =R,即方程 x2-2x+a=0 有两个相等的根,
∴Δ=4-4a=0,∴a=1.
直线与圆的位置关系
定义
性质
判定
相离
相切
相交
公共点的个数
d与r的数量关系
定义法
性质法
特别提醒:若图中没有d要先作出该垂线段
相离:0个
相切:1个
相交:2个
相离:d>r
相切:d=r
相交:d
d>r:相离
d=r:相切
d
谢谢聆听
