24.4.2切线的性质和判定 课件(共30张PPT)
文档属性
| 名称 | 24.4.2切线的性质和判定 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-28 20:24:50 | ||
图片预览






文档简介
第2课时
切线的性质和判定
24.4 直线与圆的位置关系
24章 圆
2020-2021学年度沪科版九年级下册
1. 会判定一条直线是否是圆的切线,并会过圆上一点作圆的切线.
2. 理解并掌握圆的切线的性质定理及判定定理.(重点)
3. 能运用圆的切线的性质定理和判定定理解决问题.(难点)
学习目标
转动雨伞时飞出的雨滴,用砂轮磨刀时擦出的火花,都是沿着什么方向飞出的?
都是沿切线方向飞出的.
生活中常看到切线的实例,如何判断一条直线是否为圆的切线呢?学完这节课,你就都会明白.
新课导入
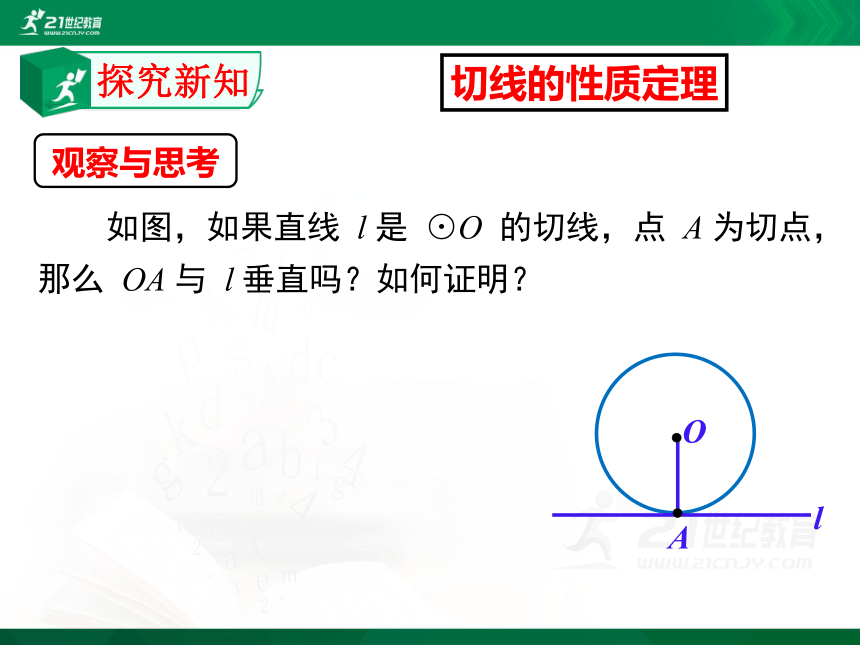
如图,如果直线 l 是 ⊙O 的切线,点 A 为切点,那么 OA 与 l 垂直吗?如何证明?
A
l
O
切线的性质定理
观察与思考
探究新知
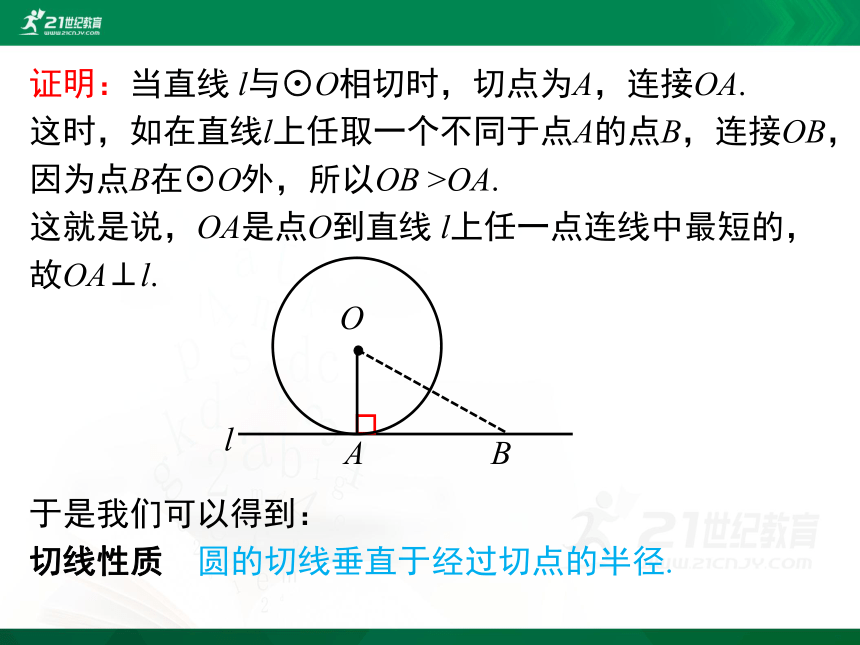
证明:当直线 l与⊙O相切时,切点为A,连接OA.
这时,如在直线l上任取一个不同于点A的点B,连接OB,
因为点B在⊙O外,所以OB >OA.
这就是说,OA是点O到直线 l上任一点连线中最短的,
故OA⊥l.
于是我们可以得到:
切线性质 圆的切线垂直于经过切点的半径.
B
A
O
l
A
l
O
∵直线l是⊙O 的切线,A是切点,
∴直线l ⊥OA.
切线性质:
圆的切线垂直于经过切点的半径.
应用格式:
知识要点
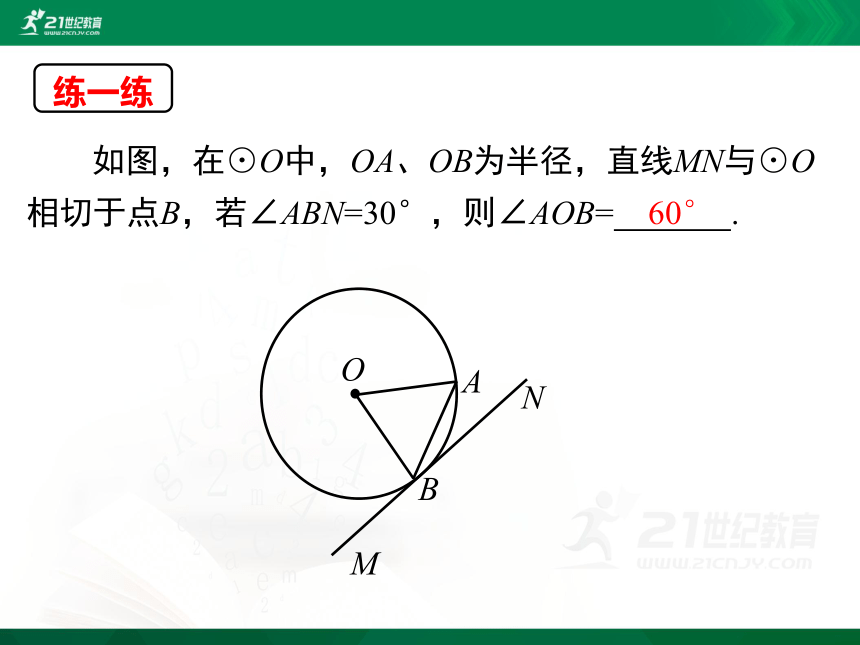
如图,在⊙O中,OA、OB为半径,直线MN与⊙O相切于点B,若∠ABN=30°,则∠AOB= .
60°
练一练
A
B
N
O
M
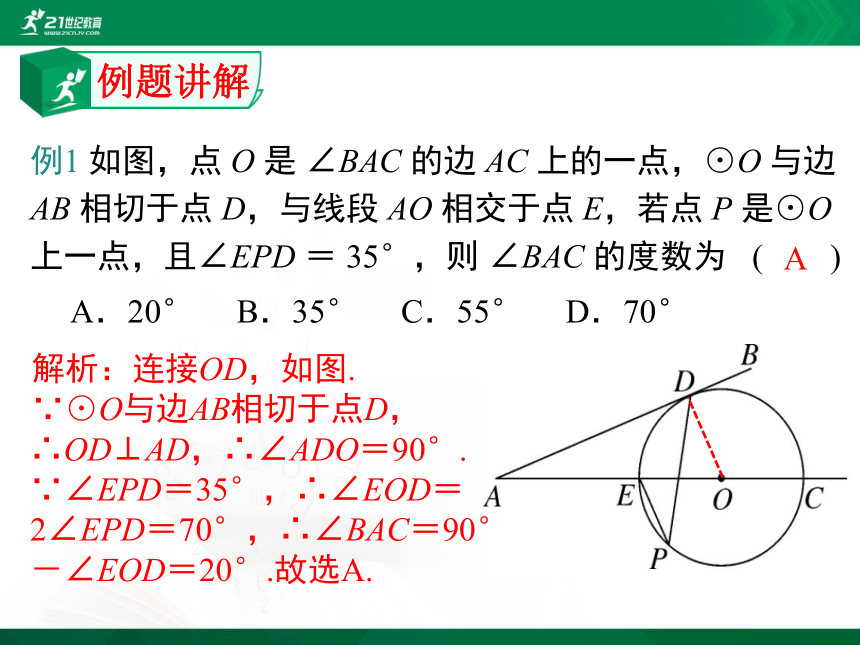
例1 如图,点 O 是 ∠BAC 的边 AC 上的一点,⊙O 与边 AB 相切于点 D,与线段 AO 相交于点 E,若点 P 是⊙O 上一点,且∠EPD = 35°,则 ∠BAC 的度数为 ( )
A.20° B.35° C.55° D.70°
解析:连接OD,如图.
∵⊙O与边AB相切于点D,∴OD⊥AD,∴∠ADO=90°. ∵∠EPD=35°,∴∠EOD=2∠EPD=70°,∴∠BAC=90°-∠EOD=20°.故选A.
A
例题讲解
例2 如图,PA为⊙O的切线,A为切点.直线PO与⊙O交于 B、C 两点,∠P=30°,连接AO、AB、AC.
(1) 求证:△ACB≌△APO;
O
A
B
P
C
在△ACB和△APO中,
∠BAC=∠OAP,AB=AO,∠ABO=∠AOB,
∴△ACB≌△APO.
证明:∵PA为⊙O的切线,A为切点,
又∵∠P=30°,OA,OB为半径,
∴∠AOB=60°,△AOB为等边三角形.
∴AB=AO,∠ABO=60°.
又∵BC为⊙O的直径,
∴∠BAC=90°.
∴∠OAP=90°.
(2) 若AP = ,求⊙O的半径.
∴ AO=1,
即⊙O的半径为1.
解:在Rt△AOP中,∠P=30°,AP= ,
O
A
B
P
C
A
B
C
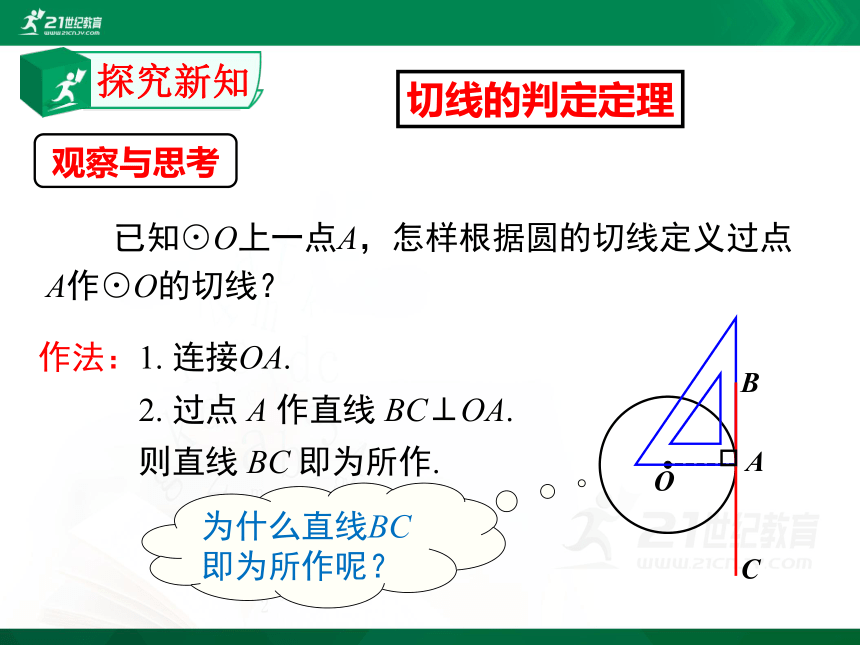
已知⊙O上一点A,怎样根据圆的切线定义过点 A作⊙O的切线?
作法:1. 连接OA.
2. 过点 A 作直线 BC⊥OA.
则直线 BC 即为所作.
切线的判定定理
O
观察与思考
为什么直线BC即为所作呢?
探究新知
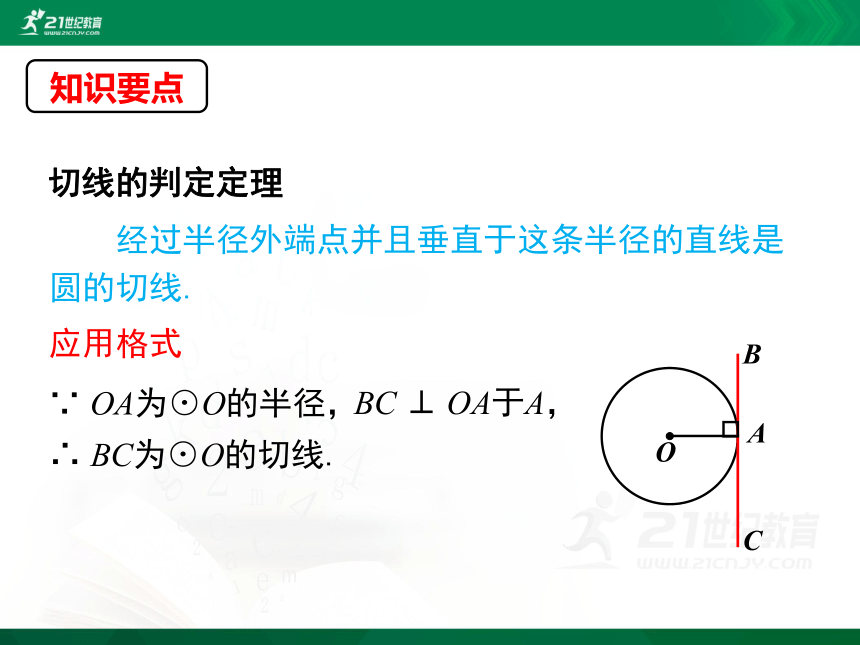
经过半径外端点并且垂直于这条半径的直线是圆的切线.
∵ OA为⊙O的半径,
BC ⊥ OA于A,
∴ BC为⊙O的切线.
A
B
C
切线的判定定理
应用格式
O
知识要点
利用切线判定定理,判断下列各直线是不是圆的切线?如果不是,请说明理由.
O.
O
O
(1)
(2)
(3)
(1) 不是,因为没有垂直.
(2),(3)不是,因为没有经过半径的外端点.
练一练
“经过半径的外端点”和“垂直于这条半径”,两个条件缺一不可,否则就不是圆的切线.
判断一条直线是一个圆的切线有三个方法:
1. 定义法:直线和圆只有一个公共点
时,我们说这条直线是圆的切线.
2. 数量关系法:圆心到这条直线的距
离等于半径 (即 d = r) 时,直线与
圆相切.
3. 判定定理:经过半径外端且垂直
于这条半径的直线是圆的切线.
l
A
l
O
l
r
d
知识要点
例3 如图,∠ABC=45°,AB是☉O的直径,AB=AC.
求证:AC是☉O的切线.
提示:直线AC经过半径的一端,因此只要证AB垂直于AC即可.
证明:∵AB =AC,∠ABC =45°,
∴∠ACB =∠ABC =45°.
∴∠BAC =180°-∠ABC-ACB =90°.
∵AB是☉O的直径,
∴ AC是☉O的切线.
A
O
C
B
例4 已知:直线 AB 经过 ☉O 上的点 C,并且OA=OB,CA = CB. 求证:直线AB是☉O的切线.
O
B
A
C
提示:由于AB过☉O上的点C,所以连接OC,只要证明OC⊥AB即可.
证明:连接OC,如图.
∵ OA=OB,CA=CB,
∴△OAB是等腰三角形,OC⊥AB.
∵ OC是⊙O的半径,
∴ AB是⊙O的切线.
例5 如图,△ABC 中,AB =AC ,O 是 BC 的中点,
⊙O 与 AB 相切于 E.求证:AC 是⊙O 的切线.
B
O
C
E
A
提示:根据切线的判定定理,要证明AC是⊙O的切线,只要证明由点O向AC所作的垂线段OF是⊙O的半径就可以了,而OE是⊙O的半径,因此只需要证明OF=OE.
F
证明:连接OE ,OA,过O 作OF ⊥AC,如图.
∵ ⊙O 与AB 相切于E,∴OE ⊥ AB.
又∵△ABC 中,AB =AC ,O 是BC 的中点.
∴AO 平分∠BAC.
F
B
O
C
E
A
∴ OE =OF.
∴ AC 是⊙O 的切线.
又∵ OE ⊥AB ,OF⊥AC.
∵OE为⊙O 半径,
∴OF为⊙O 半径.
如图,已知直线AB经过⊙O上的点C,并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线.
C
B
A
O
如图,OA=OB=5,AB=8, ⊙O的直径为6.
求证:直线AB是⊙O的切线.
C
B
A
O
通过对比,你能得出什么结论?
作垂直
连接
方法归纳
(1) 有交点,连半径,证垂直 (如:例4);
(2) 无交点,作垂直,证半径 (如:例5).
?证切线时辅助线的添加方法
?有切线时常用辅助线添加方法
见切点,连半径,得垂直 (如:例1).
要点归纳
1. 判断下列命题是否正确.
(1) 经过半径外端的直线是圆的切线. ( )
(2) 垂直于半径的直线是圆的切线. ( )
(3) 过直径的外端点并且垂直于这条直径的直线是圆
的切线. ( )
(4) 和圆只有一个公共点的直线是圆的切线. ( )
(5) 过直径一端点且垂直于直径的直线是圆的切线.
( )
×
×
√
√
√
课堂练习
3. 如图,在☉O 的内接四边形 ABCD 中,AB 是直径,
∠BCD =120°,过 D 点的切线 PD 与直线AB 交于
点P,则 ∠ADP 的度数为 ( )
A.40° B.35° C.30° D.45°
2. 如图,A 是☉O上一点,且 AO = 5,PO = 13, AP =
12,则 PA 与☉O 的位置关系是 .
A
P
O
第2题图
相切
C
P
O
第3题图
D
A
B
C
4. 如图,☉O切PB于点B,PB=4,PA=2,则☉O的半径
多少?
O
P
B
A
解:连接OB,如图.则∠OBP=90°.
设⊙O的半径为r,则
OA=OB=r,OP=OA+PA=r +2.
在Rt△OBP中,
OB2 + PB2=PO2,
即r2 + 42= (2+r)2.
解得 r=3,
即⊙O的半径为3.
O
A
B
C
E
P
5. 如图,△ABC中,AB=AC,以AB为直径的⊙O交边BC于P, PE⊥AC于E.
求证:PE是⊙O的切线.
证明:连接OP,如图.
∵AB=AC,∴∠B=∠C.
∵OB=OP,∴∠B=∠OPB,
∴∠OPB=∠C.
∴OP∥AC.
∵PE⊥AC,
∴PE⊥OP.
∴PE为⊙O的切线.
6. 如图,O 为正方形 ABCD 对角线 AC 上一点,以 O 为
圆心,OA 长为半径的 ⊙O 与 BC 相切于点 M.
求证:CD 与⊙O相切.
证明:连接OM,过点O作ON⊥CD于点N,如图.
∵ ⊙O与BC相切于点M,
∴OM⊥BC.
又∵ON⊥CD,O为正方形ABCD 对角线 AC 上一点,
∴OM=ON,
∴CD与⊙O相切.
M
N
7. 已知:△ABC内接于☉O,过点A作直线EF.
(1) 如图1,AB为直径,要使EF为☉O的切线,还需添
加的条件是(只需写出两种情况):
① _________ ;② _____________ .
(2) 如图2,AB是非直径的弦,∠CAE=∠B,求证:EF
是☉O的切线.
BA⊥EF
∠CAE=∠B
A
F
E
O
A
F
E
O
B
C
B
C
图1
图2
证明:如图,连接AO并延长交☉O于D,连接CD,则AD为☉O的直径.
∴ ∠D + ∠DAC=90 °,
∵ AC = AC ,
∴ ∠D= ∠B.
又∵ ∠CAE= ∠B,
∴ ∠D= ∠CAE,
∴ ∠CAE+ ∠DAC=90°,
即AD⊥EF,
∴ EF是☉O的切线.
A
F
E
O
B
C
图2
D
⌒
⌒
切线的
判定方法
定义法
数量关系法
判定定理
1个公共点,则相切
d=r,则相切
经过半径外端点并且垂直于这条半径的直线是圆的切线.
切线的
性质
证切线时常用辅助线添加方法:
①有公共点,连半径,证垂直;
②无公共点,作垂直,证半径.
有1个公共点
d=r
性质定理
圆的切线垂直于经过切点的半径
有切线时常用辅助线
添加方法:
见切线,连切点,得垂直.
课堂小结
谢谢聆听
切线的性质和判定
24.4 直线与圆的位置关系
24章 圆
2020-2021学年度沪科版九年级下册
1. 会判定一条直线是否是圆的切线,并会过圆上一点作圆的切线.
2. 理解并掌握圆的切线的性质定理及判定定理.(重点)
3. 能运用圆的切线的性质定理和判定定理解决问题.(难点)
学习目标
转动雨伞时飞出的雨滴,用砂轮磨刀时擦出的火花,都是沿着什么方向飞出的?
都是沿切线方向飞出的.
生活中常看到切线的实例,如何判断一条直线是否为圆的切线呢?学完这节课,你就都会明白.
新课导入
如图,如果直线 l 是 ⊙O 的切线,点 A 为切点,那么 OA 与 l 垂直吗?如何证明?
A
l
O
切线的性质定理
观察与思考
探究新知
证明:当直线 l与⊙O相切时,切点为A,连接OA.
这时,如在直线l上任取一个不同于点A的点B,连接OB,
因为点B在⊙O外,所以OB >OA.
这就是说,OA是点O到直线 l上任一点连线中最短的,
故OA⊥l.
于是我们可以得到:
切线性质 圆的切线垂直于经过切点的半径.
B
A
O
l
A
l
O
∵直线l是⊙O 的切线,A是切点,
∴直线l ⊥OA.
切线性质:
圆的切线垂直于经过切点的半径.
应用格式:
知识要点
如图,在⊙O中,OA、OB为半径,直线MN与⊙O相切于点B,若∠ABN=30°,则∠AOB= .
60°
练一练
A
B
N
O
M
例1 如图,点 O 是 ∠BAC 的边 AC 上的一点,⊙O 与边 AB 相切于点 D,与线段 AO 相交于点 E,若点 P 是⊙O 上一点,且∠EPD = 35°,则 ∠BAC 的度数为 ( )
A.20° B.35° C.55° D.70°
解析:连接OD,如图.
∵⊙O与边AB相切于点D,∴OD⊥AD,∴∠ADO=90°. ∵∠EPD=35°,∴∠EOD=2∠EPD=70°,∴∠BAC=90°-∠EOD=20°.故选A.
A
例题讲解
例2 如图,PA为⊙O的切线,A为切点.直线PO与⊙O交于 B、C 两点,∠P=30°,连接AO、AB、AC.
(1) 求证:△ACB≌△APO;
O
A
B
P
C
在△ACB和△APO中,
∠BAC=∠OAP,AB=AO,∠ABO=∠AOB,
∴△ACB≌△APO.
证明:∵PA为⊙O的切线,A为切点,
又∵∠P=30°,OA,OB为半径,
∴∠AOB=60°,△AOB为等边三角形.
∴AB=AO,∠ABO=60°.
又∵BC为⊙O的直径,
∴∠BAC=90°.
∴∠OAP=90°.
(2) 若AP = ,求⊙O的半径.
∴ AO=1,
即⊙O的半径为1.
解:在Rt△AOP中,∠P=30°,AP= ,
O
A
B
P
C
A
B
C
已知⊙O上一点A,怎样根据圆的切线定义过点 A作⊙O的切线?
作法:1. 连接OA.
2. 过点 A 作直线 BC⊥OA.
则直线 BC 即为所作.
切线的判定定理
O
观察与思考
为什么直线BC即为所作呢?
探究新知
经过半径外端点并且垂直于这条半径的直线是圆的切线.
∵ OA为⊙O的半径,
BC ⊥ OA于A,
∴ BC为⊙O的切线.
A
B
C
切线的判定定理
应用格式
O
知识要点
利用切线判定定理,判断下列各直线是不是圆的切线?如果不是,请说明理由.
O.
O
O
(1)
(2)
(3)
(1) 不是,因为没有垂直.
(2),(3)不是,因为没有经过半径的外端点.
练一练
“经过半径的外端点”和“垂直于这条半径”,两个条件缺一不可,否则就不是圆的切线.
判断一条直线是一个圆的切线有三个方法:
1. 定义法:直线和圆只有一个公共点
时,我们说这条直线是圆的切线.
2. 数量关系法:圆心到这条直线的距
离等于半径 (即 d = r) 时,直线与
圆相切.
3. 判定定理:经过半径外端且垂直
于这条半径的直线是圆的切线.
l
A
l
O
l
r
d
知识要点
例3 如图,∠ABC=45°,AB是☉O的直径,AB=AC.
求证:AC是☉O的切线.
提示:直线AC经过半径的一端,因此只要证AB垂直于AC即可.
证明:∵AB =AC,∠ABC =45°,
∴∠ACB =∠ABC =45°.
∴∠BAC =180°-∠ABC-ACB =90°.
∵AB是☉O的直径,
∴ AC是☉O的切线.
A
O
C
B
例4 已知:直线 AB 经过 ☉O 上的点 C,并且OA=OB,CA = CB. 求证:直线AB是☉O的切线.
O
B
A
C
提示:由于AB过☉O上的点C,所以连接OC,只要证明OC⊥AB即可.
证明:连接OC,如图.
∵ OA=OB,CA=CB,
∴△OAB是等腰三角形,OC⊥AB.
∵ OC是⊙O的半径,
∴ AB是⊙O的切线.
例5 如图,△ABC 中,AB =AC ,O 是 BC 的中点,
⊙O 与 AB 相切于 E.求证:AC 是⊙O 的切线.
B
O
C
E
A
提示:根据切线的判定定理,要证明AC是⊙O的切线,只要证明由点O向AC所作的垂线段OF是⊙O的半径就可以了,而OE是⊙O的半径,因此只需要证明OF=OE.
F
证明:连接OE ,OA,过O 作OF ⊥AC,如图.
∵ ⊙O 与AB 相切于E,∴OE ⊥ AB.
又∵△ABC 中,AB =AC ,O 是BC 的中点.
∴AO 平分∠BAC.
F
B
O
C
E
A
∴ OE =OF.
∴ AC 是⊙O 的切线.
又∵ OE ⊥AB ,OF⊥AC.
∵OE为⊙O 半径,
∴OF为⊙O 半径.
如图,已知直线AB经过⊙O上的点C,并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线.
C
B
A
O
如图,OA=OB=5,AB=8, ⊙O的直径为6.
求证:直线AB是⊙O的切线.
C
B
A
O
通过对比,你能得出什么结论?
作垂直
连接
方法归纳
(1) 有交点,连半径,证垂直 (如:例4);
(2) 无交点,作垂直,证半径 (如:例5).
?证切线时辅助线的添加方法
?有切线时常用辅助线添加方法
见切点,连半径,得垂直 (如:例1).
要点归纳
1. 判断下列命题是否正确.
(1) 经过半径外端的直线是圆的切线. ( )
(2) 垂直于半径的直线是圆的切线. ( )
(3) 过直径的外端点并且垂直于这条直径的直线是圆
的切线. ( )
(4) 和圆只有一个公共点的直线是圆的切线. ( )
(5) 过直径一端点且垂直于直径的直线是圆的切线.
( )
×
×
√
√
√
课堂练习
3. 如图,在☉O 的内接四边形 ABCD 中,AB 是直径,
∠BCD =120°,过 D 点的切线 PD 与直线AB 交于
点P,则 ∠ADP 的度数为 ( )
A.40° B.35° C.30° D.45°
2. 如图,A 是☉O上一点,且 AO = 5,PO = 13, AP =
12,则 PA 与☉O 的位置关系是 .
A
P
O
第2题图
相切
C
P
O
第3题图
D
A
B
C
4. 如图,☉O切PB于点B,PB=4,PA=2,则☉O的半径
多少?
O
P
B
A
解:连接OB,如图.则∠OBP=90°.
设⊙O的半径为r,则
OA=OB=r,OP=OA+PA=r +2.
在Rt△OBP中,
OB2 + PB2=PO2,
即r2 + 42= (2+r)2.
解得 r=3,
即⊙O的半径为3.
O
A
B
C
E
P
5. 如图,△ABC中,AB=AC,以AB为直径的⊙O交边BC于P, PE⊥AC于E.
求证:PE是⊙O的切线.
证明:连接OP,如图.
∵AB=AC,∴∠B=∠C.
∵OB=OP,∴∠B=∠OPB,
∴∠OPB=∠C.
∴OP∥AC.
∵PE⊥AC,
∴PE⊥OP.
∴PE为⊙O的切线.
6. 如图,O 为正方形 ABCD 对角线 AC 上一点,以 O 为
圆心,OA 长为半径的 ⊙O 与 BC 相切于点 M.
求证:CD 与⊙O相切.
证明:连接OM,过点O作ON⊥CD于点N,如图.
∵ ⊙O与BC相切于点M,
∴OM⊥BC.
又∵ON⊥CD,O为正方形ABCD 对角线 AC 上一点,
∴OM=ON,
∴CD与⊙O相切.
M
N
7. 已知:△ABC内接于☉O,过点A作直线EF.
(1) 如图1,AB为直径,要使EF为☉O的切线,还需添
加的条件是(只需写出两种情况):
① _________ ;② _____________ .
(2) 如图2,AB是非直径的弦,∠CAE=∠B,求证:EF
是☉O的切线.
BA⊥EF
∠CAE=∠B
A
F
E
O
A
F
E
O
B
C
B
C
图1
图2
证明:如图,连接AO并延长交☉O于D,连接CD,则AD为☉O的直径.
∴ ∠D + ∠DAC=90 °,
∵ AC = AC ,
∴ ∠D= ∠B.
又∵ ∠CAE= ∠B,
∴ ∠D= ∠CAE,
∴ ∠CAE+ ∠DAC=90°,
即AD⊥EF,
∴ EF是☉O的切线.
A
F
E
O
B
C
图2
D
⌒
⌒
切线的
判定方法
定义法
数量关系法
判定定理
1个公共点,则相切
d=r,则相切
经过半径外端点并且垂直于这条半径的直线是圆的切线.
切线的
性质
证切线时常用辅助线添加方法:
①有公共点,连半径,证垂直;
②无公共点,作垂直,证半径.
有1个公共点
d=r
性质定理
圆的切线垂直于经过切点的半径
有切线时常用辅助线
添加方法:
见切线,连切点,得垂直.
课堂小结
谢谢聆听
