2.2二次函数的图象(第5课时) 典型题型 课件(共25张PPT)
文档属性
| 名称 | 2.2二次函数的图象(第5课时) 典型题型 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-28 20:30:32 | ||
图片预览







文档简介
数学北师大版
九年级
九年级数学下册北师大
2.2二次函数的图象第5课时典型题型
1.若抛物线y=x2-2x+3不动,将平面直角坐标系xOy先沿水平方向向右平移一个单位长度,再沿铅直方向向上平移三个单位长度,则原抛物线的表达式应变为( )
A.y=(x-2)2+3 B.y=(x-2)2+5
C.y=x2-1 D.y=x2+4
C
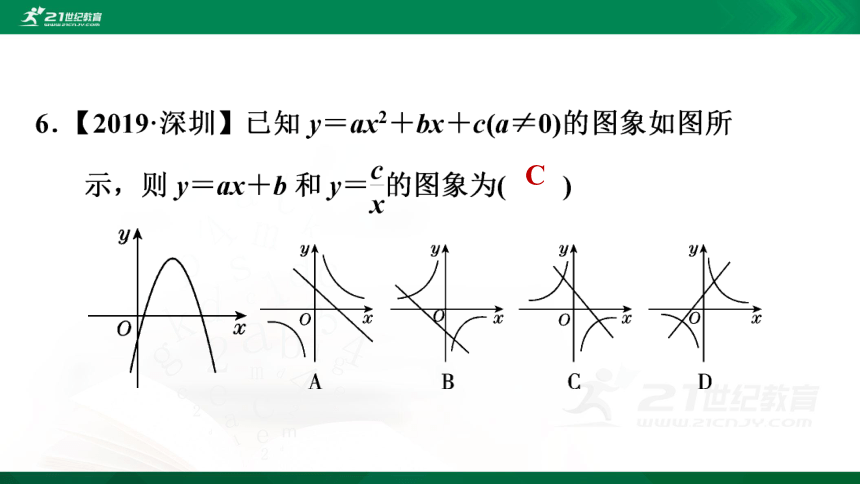
2.【2019?遂宁】二次函数y=x2-ax+b的图象如图所
示,对称轴为直线x=2,下列结论不正确的是( )
A.a=4
B.当b=-4时,顶点的坐标为(2,-8)
C.当x=-1时,b>-5
D.当x>3时,y随x的增大而增大
C
3.【2019?温州】已知二次函数y=x2-4x+2,关于该函数在-1≤x≤3的取值范围内,下列说法正确的是( )
A.有最大值-1,有最小值-2
B.有最大值0,有最小值-1
C.有最大值7,有最小值-1
D.有最大值7,有最小值-2
D
【答案】 D
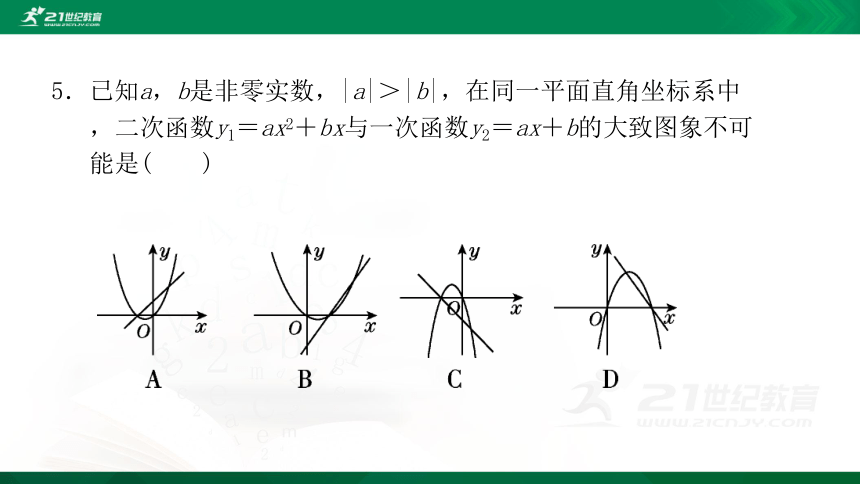
5.已知a,b是非零实数,|a|>|b|,在同一平面直角坐标系中,二次函数y1=ax2+bx与一次函数y2=ax+b的大致图象不可能是( )
【答案】 D
C
A
提示判别式小于等于0
8.已知直线l:y=kx+1与抛物线y=x2-4x.
(1)求证:直线l与该抛物线总有两个交点.
8.已知直线l:y=kx+1与抛物线y=x2-4x.
(2)设直线l与该抛物线的两个交点为A,B,O为原点,
当k=-2时,求△OAB的面积.
解:将点(-2,4)的坐标代入y=x2+bx+c,
得-2b+c=0,∴c=2b.
9.已知函数y=x2+bx+c(b,c为常数)的图象经过点(-2,4).
(1)求b,c满足的关系式;
(2)设该函数图象的顶点坐标是(m,n),当b的值变化时,求n关于m的函数表达式;
【点拨】将b的值分成几段进行分段讨论.
9已知函数y=x2+bx+c(b,c为常数)的图象经过点(-2,4).
(3)若该函数的图象不经过第三象限,当-5≤x≤1时,函数
的最大值与最小值之差为16,求b的值.
此时y=x2,当-5≤x≤1时,函数的最小值是0,最大值是25, ∴最大值与最小值之差是25(不合题意,舍去).
当b>0时,c>0,函数的图象不经过第三象限,
(2)指出二次函数y=a(x-h)2+k图象的开口方向、对称轴和顶点坐标.
解:二次函数y=a(x-h)2+k图象的开口向上,对称轴为直线x=1,顶点坐标为(1,-5).
11.【中考?天水】如图,排球运动员站在点O处练习发球,将球从O点正上方2 m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的水平距离为9 m,高度为2.43 m,
球场的边界距O点的水平距离为18 m.
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围).
解:∵球从O点正上方2 m的A处发出, ∴抛物线y=a(x-6)2+h过点(0,2). 又∵h=2.6,∴2=a(0-6)2+2.6.解得
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由.
(3)若球一定能越过球网,又不出边界,求h的取值范围.
12.如图,已知抛物线y=a(x-h)2+k与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),对称轴为直线x=1.
(1)求抛物线对应的函数表达式;
【点拨】根据等腰三角形的两腰相等,
利用分类讨论思想分成三种情况.①
MA=MB;②AB=AM;③AB=BM,
分别对这三种情况讨论.
(2)已知点M为y轴上的一个动点,当△ABM为等腰三角形时,求点M的坐标.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
九年级
九年级数学下册北师大
2.2二次函数的图象第5课时典型题型
1.若抛物线y=x2-2x+3不动,将平面直角坐标系xOy先沿水平方向向右平移一个单位长度,再沿铅直方向向上平移三个单位长度,则原抛物线的表达式应变为( )
A.y=(x-2)2+3 B.y=(x-2)2+5
C.y=x2-1 D.y=x2+4
C
2.【2019?遂宁】二次函数y=x2-ax+b的图象如图所
示,对称轴为直线x=2,下列结论不正确的是( )
A.a=4
B.当b=-4时,顶点的坐标为(2,-8)
C.当x=-1时,b>-5
D.当x>3时,y随x的增大而增大
C
3.【2019?温州】已知二次函数y=x2-4x+2,关于该函数在-1≤x≤3的取值范围内,下列说法正确的是( )
A.有最大值-1,有最小值-2
B.有最大值0,有最小值-1
C.有最大值7,有最小值-1
D.有最大值7,有最小值-2
D
【答案】 D
5.已知a,b是非零实数,|a|>|b|,在同一平面直角坐标系中,二次函数y1=ax2+bx与一次函数y2=ax+b的大致图象不可能是( )
【答案】 D
C
A
提示判别式小于等于0
8.已知直线l:y=kx+1与抛物线y=x2-4x.
(1)求证:直线l与该抛物线总有两个交点.
8.已知直线l:y=kx+1与抛物线y=x2-4x.
(2)设直线l与该抛物线的两个交点为A,B,O为原点,
当k=-2时,求△OAB的面积.
解:将点(-2,4)的坐标代入y=x2+bx+c,
得-2b+c=0,∴c=2b.
9.已知函数y=x2+bx+c(b,c为常数)的图象经过点(-2,4).
(1)求b,c满足的关系式;
(2)设该函数图象的顶点坐标是(m,n),当b的值变化时,求n关于m的函数表达式;
【点拨】将b的值分成几段进行分段讨论.
9已知函数y=x2+bx+c(b,c为常数)的图象经过点(-2,4).
(3)若该函数的图象不经过第三象限,当-5≤x≤1时,函数
的最大值与最小值之差为16,求b的值.
此时y=x2,当-5≤x≤1时,函数的最小值是0,最大值是25, ∴最大值与最小值之差是25(不合题意,舍去).
当b>0时,c>0,函数的图象不经过第三象限,
(2)指出二次函数y=a(x-h)2+k图象的开口方向、对称轴和顶点坐标.
解:二次函数y=a(x-h)2+k图象的开口向上,对称轴为直线x=1,顶点坐标为(1,-5).
11.【中考?天水】如图,排球运动员站在点O处练习发球,将球从O点正上方2 m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的水平距离为9 m,高度为2.43 m,
球场的边界距O点的水平距离为18 m.
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围).
解:∵球从O点正上方2 m的A处发出, ∴抛物线y=a(x-6)2+h过点(0,2). 又∵h=2.6,∴2=a(0-6)2+2.6.解得
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由.
(3)若球一定能越过球网,又不出边界,求h的取值范围.
12.如图,已知抛物线y=a(x-h)2+k与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),对称轴为直线x=1.
(1)求抛物线对应的函数表达式;
【点拨】根据等腰三角形的两腰相等,
利用分类讨论思想分成三种情况.①
MA=MB;②AB=AM;③AB=BM,
分别对这三种情况讨论.
(2)已知点M为y轴上的一个动点,当△ABM为等腰三角形时,求点M的坐标.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
