3.3 垂径定理 课件(共23张PPT)
文档属性
| 名称 | 3.3 垂径定理 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-01 07:27:08 | ||
图片预览





文档简介
数学北师大版
九年级
3.3 垂径定理
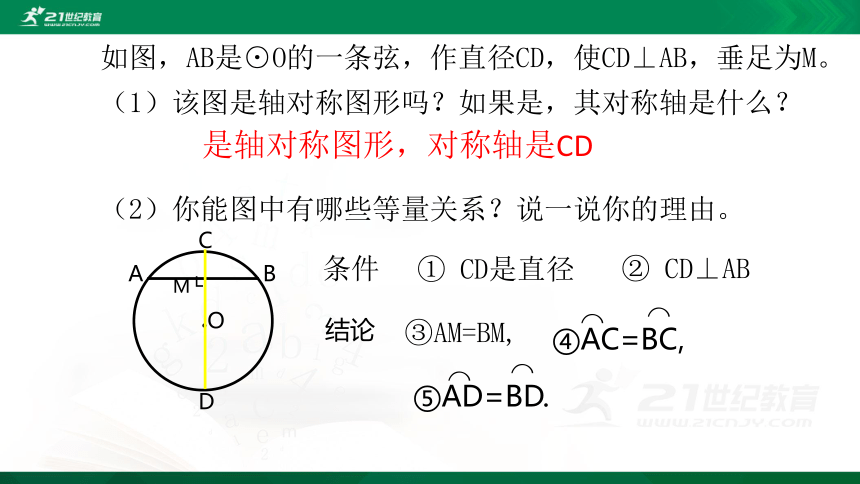
③AM=BM,
●O
A
B
C
D
M└
① CD是直径
② CD⊥AB
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
条件
结论
如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为M。
(1)该图是轴对称图形吗?如果是,其对称轴是什么?
(2)你能图中有哪些等量关系?说一说你的理由。
是轴对称图形,对称轴是CD
垂径定理
·
O
A
B
C
D
P
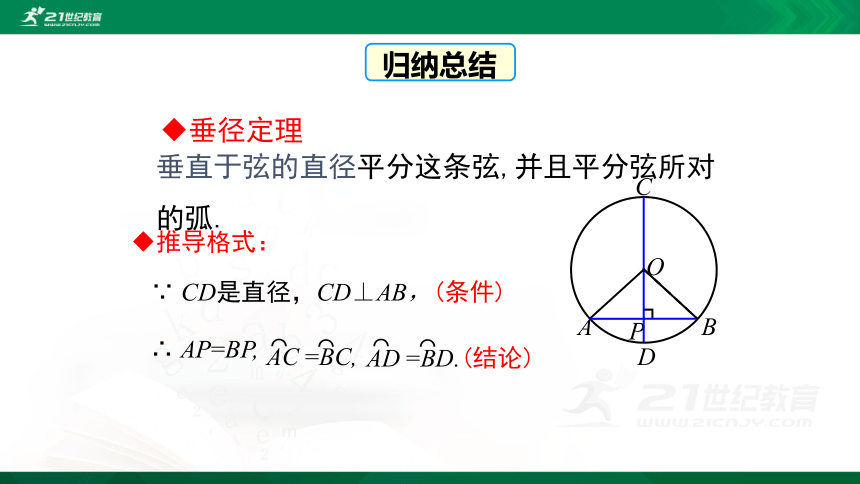
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
∵ CD是直径,CD⊥AB,(条件)
∴ AP=BP,
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.(结论)
归纳总结
推导格式:
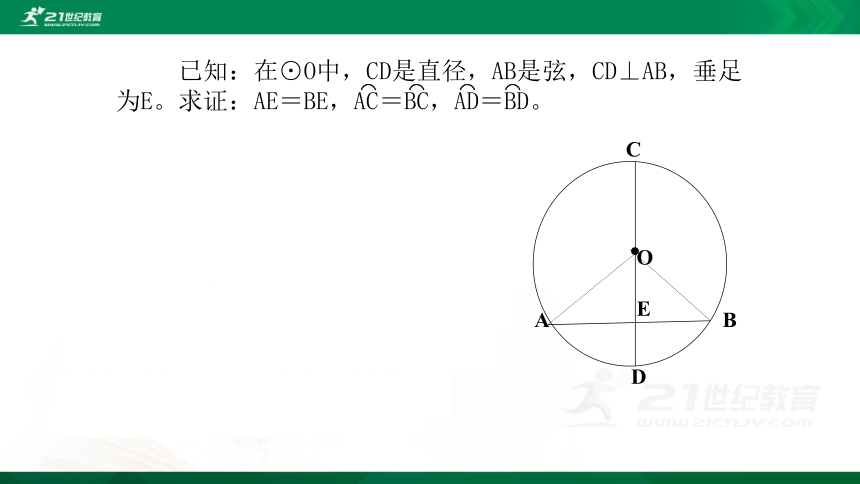
已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E。求证:AE=BE,AC=BC,AD=BD。
⌒
⌒
⌒
⌒
证明:连结OA、OB,则OA=OB。因为垂直于弦AB的直径CD所在的直线既是等腰三角形OAB的对称轴又是⊙ O的对称轴。所以,当把圆沿着直径CD折叠时,CD两侧的两个半圆重合,A点和B点重合,AE和BE重合,AC、AD分别和BC、BD重合。因此 AE=BE,AC=BC,AD=BD
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
C
.
O
A
E
B
D
∵CD⊥AB,
∴AM = BM,∠AOC = ∠BOC,
∴ = ,
∵∠AOD = 180°- ∠AOC,
∠BOD = 180°- ∠BOC,
∴ ∠AOD = ∠BOD
∴ = .
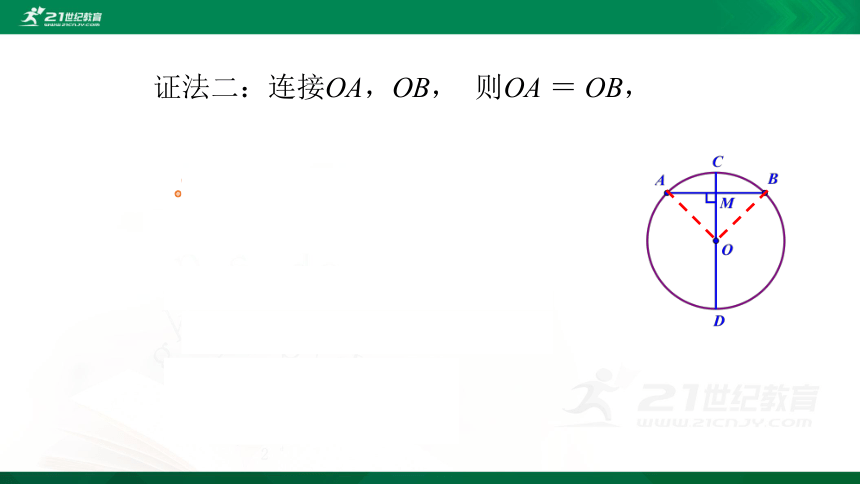
证法二:连接OA,OB, 则OA = OB,
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
几何语言叙述定理:
∵CD为⊙O的直径,且CD⊥AB,
∴AM=BM, = , = .
知识点一:垂径定理
如图,AB是⊙O的弦(不是直径),作一条平分AB的直径CD,交AB于点M.
(1)上图是轴对称图形吗?如果是,其对称轴是什么?
(2)你能发现图中有哪些等量关系?说一说你的理由.
上图是轴对称图形,对称轴是CD.
AM=BM
想一想:
求证:平分弦 (不是直径) 的直径垂直于弦,
并且平分弦所对的弧.
已知,如图,AB是⊙O的一条弦,CD是⊙O
的一条直径,CD交AB于点M,且AM=BM,
求证:CD⊥AB, = , = .
证明:连接OA,OB,则OA=OB,
∵ AM=BM ,∴ CD⊥AB ,∠AOC=∠BOC,
∴ = ,
∵∠AOD = 180°-∠AOC,∠BOD = 180°-∠BOC,
∴ ∠AOD = ∠BOD ∴ = .
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
几何语言叙述定理:
垂径定理的逆定理
∵AM = BM,CD为⊙O的直径,
∴CD⊥AB, = , = .
已知其中两个条件,就可推出其余三个结论。
如图,在同圆中,如果具备下列条件:
(1)CD是直径;
(2)CD⊥AB;
(3)AM = BM;
(4) = ;
(5) = ,
1.平分弦所对的弧 2.平分弦 (不是直径)3.垂直于弦 4.经过圆心
例如图,一 条公路的转弯处是一段弧(即
图中 ,点O是 所在圆的圆心).其中
CD=600m,E为 上一点,且OE⊥CD,垂足
为F,EF=90m.求这段弯路的半径.
解:连接OC,设弯路的半径为Rm,则:OF=(R-90)m,
∵OE⊥CD,∴CF= CD = ×600 = 300(m),
在Rt△OCF中,由勾股定理得:
OC2=CF2+OF2,∴R2=3002+(R-90)2
解得:R=545,
∴这段弯路的半径为545m.
例2 已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
求证:AC=BD。
则AE=BE,CE=DE。
AE-CE=BE-DE。
所以,AC=BD
E
.
A
C
D
B
O
证明:过O作OE⊥AB,垂足为E,
┐
练习.如果圆的两条弦互相平行,那么这两条弦所夹的弧相等吗?为什么?
提示:
这两条弦在圆中位置有两种情况。
(1)两条弦在圆心的同侧
(2)两条弦在圆心的两侧
1.两条弦在圆心的同侧
证明:连接OA、OB、OC、OD,
作直径MN⊥AB,则MN⊥CD,
由垂径定理,得:
= , = ,
∴∠AON =∠BON,∠CON = ∠DON
∴∠AON-∠CON = ∠BON - ∠DON
即 ∠AOC = ∠BOD
∴ =
2.两条弦在圆心的两侧
证明:连接OA、OB、OC、OD,
作直径MN⊥AB,则MN⊥CD,
由垂径定理,得:
= , = ,
∴∠AOM=∠BOM,∠CON=∠DON
∵∠AOM+∠AOC + ∠CON=180°
∠BOM + ∠BOD + ∠DON=180°
∴ ∠AOC=∠BOD
∴ =
圆的两条平行弦所夹的弧相等
1.圆的相关概念,弦、弧、优弧、劣弧.
2.垂径定理及推论、圆的对称性.
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
通过本课时的学习,需要我们掌握:
课后作业
1.如图是某风景区的一个圆拱形门,路面AB宽为2米,净高5米,求圆拱形门所在圆的半径是多少米.
2.如图所示,在一直径为8 m的圆形戏水池中搭有两座浮桥AB,CD.已知C是AB的中点,浮桥CD的长为4 m,设AB,CD交于点P,试求∠APC的度数.
3.如图,某地有一座圆弧形拱桥,圆心为0,桥下水面跨度为7.2m,过0作0C⊥AB于点D,交圆弧于点C,CD=2.4 m,现有一-艘宽3 m、船舱顶部为长方体并高出水面AB2m的货船要经过拱桥.问此货船能否顺利地通过这座拱桥?
解:连接0A,ON,设CD交MN于点H,AB=7.2m,CD=2.4m,EF=3m,
且D为AB,EF的中点,0C⊥AB,0C⊥MN,设OA=R,
则OD=0C-DC=R-2.4,
3.6m
在Rt△OAD中,有0A2 =AD2 + 0D2,即R2=3.62+(R-2.4)2,解得R=3.9m.
在Rt△ONH中,
∴FN = DH = OH- 0D=3.6-(3.9-2.4) =2.1m>2m.
∴货船可以顺利通过这座拱桥,但要非常小心。
如图,已知☉O中EF过圆心0,且垂直于弦AD,垂足为点F,B,C两点在直线DE上,且AD平分∠BAC.求证:DE2=BE●CE.
证明:连接AE.∵EF⊥AD,且EF过圆心O
∴EF垂直平分AD.∴AE=DE.∴∠CDA=∠EAD.
∵AD平分∠BAC,∴∠BAD=∠DAC.
∵∠ECA=∠CDA+∠CAD, ∠EAB=∠EAD+∠BAD,
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
九年级
3.3 垂径定理
③AM=BM,
●O
A
B
C
D
M└
① CD是直径
② CD⊥AB
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
条件
结论
如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为M。
(1)该图是轴对称图形吗?如果是,其对称轴是什么?
(2)你能图中有哪些等量关系?说一说你的理由。
是轴对称图形,对称轴是CD
垂径定理
·
O
A
B
C
D
P
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
∵ CD是直径,CD⊥AB,(条件)
∴ AP=BP,
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.(结论)
归纳总结
推导格式:
已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E。求证:AE=BE,AC=BC,AD=BD。
⌒
⌒
⌒
⌒
证明:连结OA、OB,则OA=OB。因为垂直于弦AB的直径CD所在的直线既是等腰三角形OAB的对称轴又是⊙ O的对称轴。所以,当把圆沿着直径CD折叠时,CD两侧的两个半圆重合,A点和B点重合,AE和BE重合,AC、AD分别和BC、BD重合。因此 AE=BE,AC=BC,AD=BD
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
C
.
O
A
E
B
D
∵CD⊥AB,
∴AM = BM,∠AOC = ∠BOC,
∴ = ,
∵∠AOD = 180°- ∠AOC,
∠BOD = 180°- ∠BOC,
∴ ∠AOD = ∠BOD
∴ = .
证法二:连接OA,OB, 则OA = OB,
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
几何语言叙述定理:
∵CD为⊙O的直径,且CD⊥AB,
∴AM=BM, = , = .
知识点一:垂径定理
如图,AB是⊙O的弦(不是直径),作一条平分AB的直径CD,交AB于点M.
(1)上图是轴对称图形吗?如果是,其对称轴是什么?
(2)你能发现图中有哪些等量关系?说一说你的理由.
上图是轴对称图形,对称轴是CD.
AM=BM
想一想:
求证:平分弦 (不是直径) 的直径垂直于弦,
并且平分弦所对的弧.
已知,如图,AB是⊙O的一条弦,CD是⊙O
的一条直径,CD交AB于点M,且AM=BM,
求证:CD⊥AB, = , = .
证明:连接OA,OB,则OA=OB,
∵ AM=BM ,∴ CD⊥AB ,∠AOC=∠BOC,
∴ = ,
∵∠AOD = 180°-∠AOC,∠BOD = 180°-∠BOC,
∴ ∠AOD = ∠BOD ∴ = .
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
几何语言叙述定理:
垂径定理的逆定理
∵AM = BM,CD为⊙O的直径,
∴CD⊥AB, = , = .
已知其中两个条件,就可推出其余三个结论。
如图,在同圆中,如果具备下列条件:
(1)CD是直径;
(2)CD⊥AB;
(3)AM = BM;
(4) = ;
(5) = ,
1.平分弦所对的弧 2.平分弦 (不是直径)3.垂直于弦 4.经过圆心
例如图,一 条公路的转弯处是一段弧(即
图中 ,点O是 所在圆的圆心).其中
CD=600m,E为 上一点,且OE⊥CD,垂足
为F,EF=90m.求这段弯路的半径.
解:连接OC,设弯路的半径为Rm,则:OF=(R-90)m,
∵OE⊥CD,∴CF= CD = ×600 = 300(m),
在Rt△OCF中,由勾股定理得:
OC2=CF2+OF2,∴R2=3002+(R-90)2
解得:R=545,
∴这段弯路的半径为545m.
例2 已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
求证:AC=BD。
则AE=BE,CE=DE。
AE-CE=BE-DE。
所以,AC=BD
E
.
A
C
D
B
O
证明:过O作OE⊥AB,垂足为E,
┐
练习.如果圆的两条弦互相平行,那么这两条弦所夹的弧相等吗?为什么?
提示:
这两条弦在圆中位置有两种情况。
(1)两条弦在圆心的同侧
(2)两条弦在圆心的两侧
1.两条弦在圆心的同侧
证明:连接OA、OB、OC、OD,
作直径MN⊥AB,则MN⊥CD,
由垂径定理,得:
= , = ,
∴∠AON =∠BON,∠CON = ∠DON
∴∠AON-∠CON = ∠BON - ∠DON
即 ∠AOC = ∠BOD
∴ =
2.两条弦在圆心的两侧
证明:连接OA、OB、OC、OD,
作直径MN⊥AB,则MN⊥CD,
由垂径定理,得:
= , = ,
∴∠AOM=∠BOM,∠CON=∠DON
∵∠AOM+∠AOC + ∠CON=180°
∠BOM + ∠BOD + ∠DON=180°
∴ ∠AOC=∠BOD
∴ =
圆的两条平行弦所夹的弧相等
1.圆的相关概念,弦、弧、优弧、劣弧.
2.垂径定理及推论、圆的对称性.
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
通过本课时的学习,需要我们掌握:
课后作业
1.如图是某风景区的一个圆拱形门,路面AB宽为2米,净高5米,求圆拱形门所在圆的半径是多少米.
2.如图所示,在一直径为8 m的圆形戏水池中搭有两座浮桥AB,CD.已知C是AB的中点,浮桥CD的长为4 m,设AB,CD交于点P,试求∠APC的度数.
3.如图,某地有一座圆弧形拱桥,圆心为0,桥下水面跨度为7.2m,过0作0C⊥AB于点D,交圆弧于点C,CD=2.4 m,现有一-艘宽3 m、船舱顶部为长方体并高出水面AB2m的货船要经过拱桥.问此货船能否顺利地通过这座拱桥?
解:连接0A,ON,设CD交MN于点H,AB=7.2m,CD=2.4m,EF=3m,
且D为AB,EF的中点,0C⊥AB,0C⊥MN,设OA=R,
则OD=0C-DC=R-2.4,
3.6m
在Rt△OAD中,有0A2 =AD2 + 0D2,即R2=3.62+(R-2.4)2,解得R=3.9m.
在Rt△ONH中,
∴FN = DH = OH- 0D=3.6-(3.9-2.4) =2.1m>2m.
∴货船可以顺利通过这座拱桥,但要非常小心。
如图,已知☉O中EF过圆心0,且垂直于弦AD,垂足为点F,B,C两点在直线DE上,且AD平分∠BAC.求证:DE2=BE●CE.
证明:连接AE.∵EF⊥AD,且EF过圆心O
∴EF垂直平分AD.∴AE=DE.∴∠CDA=∠EAD.
∵AD平分∠BAC,∴∠BAD=∠DAC.
∵∠ECA=∠CDA+∠CAD, ∠EAB=∠EAD+∠BAD,
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
