3.4 圆周角和圆心角的关系(第2课时) 课件(共30张PPT)
文档属性
| 名称 | 3.4 圆周角和圆心角的关系(第2课时) 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-28 00:00:00 | ||
图片预览






文档简介
数学北师大版
九年级
3.4圆周角和圆心角的关系第2课时
1.圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角.
2.圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半.
同弧(等弧)所对的圆周角相等.
3.圆周角定理推论:
相等的圆周角所对的弧相等.
4.在同圆或等圆中,
相等的弦所对的弧不一定相等.(优劣弧的区别)
5.在同圆或等圆中,
●O
B
A
C
D
E
复习巩固
B
C
●O
A
┗
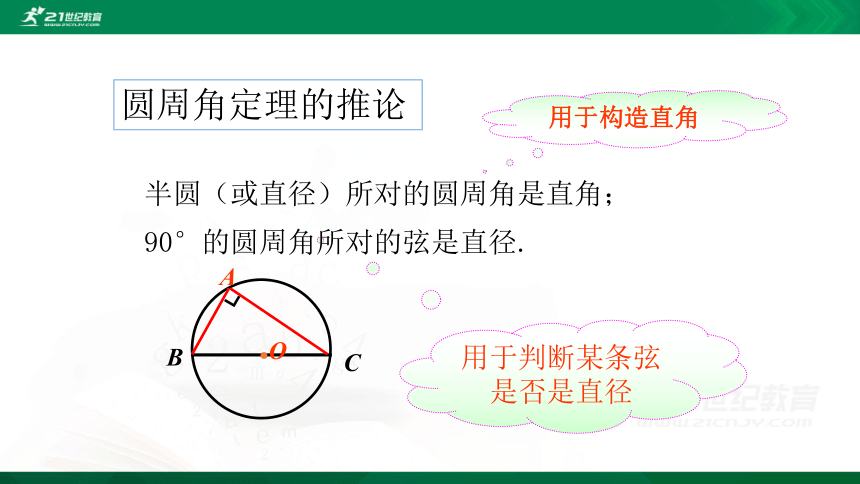
圆周角定理的推论
用于判断某条弦是否是直径
用于构造直角
半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径.
●O
D
A
B
C
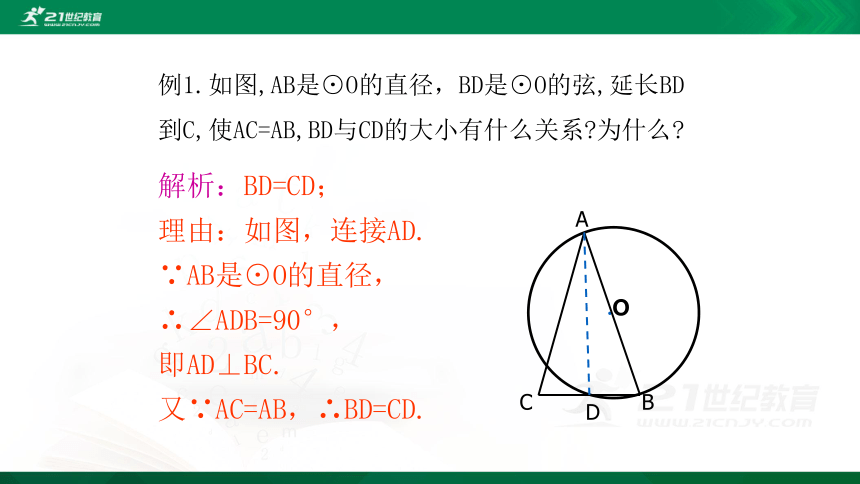
例1.如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到C,使AC=AB,BD与CD的大小有什么关系?为什么?
解析:BD=CD;
理由:如图,连接AD.
∵AB是⊙O的直径,∴∠ADB=90°,
即AD⊥BC.
又∵AC=AB,∴BD=CD.
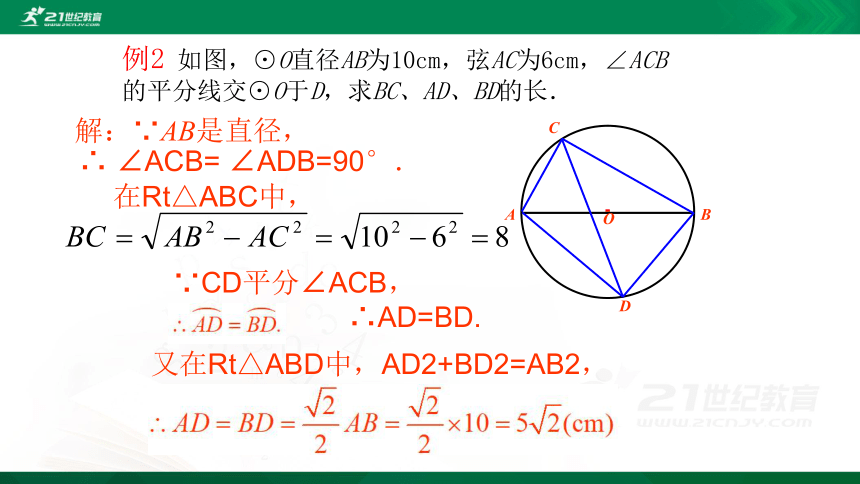
例2 如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长.
又在Rt△ABD中,AD2+BD2=AB2,
·
A
B
C
D
O
解:∵AB是直径,
∴ ∠ACB= ∠ADB=90°.
在Rt△ABC中,
∵CD平分∠ACB,
∴AD=BD.
如图A,B,C,D,是⊙O上的四点,AC为⊙O的直径,则∠BAD与∠BCD之间有什么关系?为什么?
解析:∵AC是⊙O的直径,
∴∠ADB=90° ∠ABC=90°
∴ ∠BAD+ ∠BCD
=360°-90° -90° = 180°
议一议
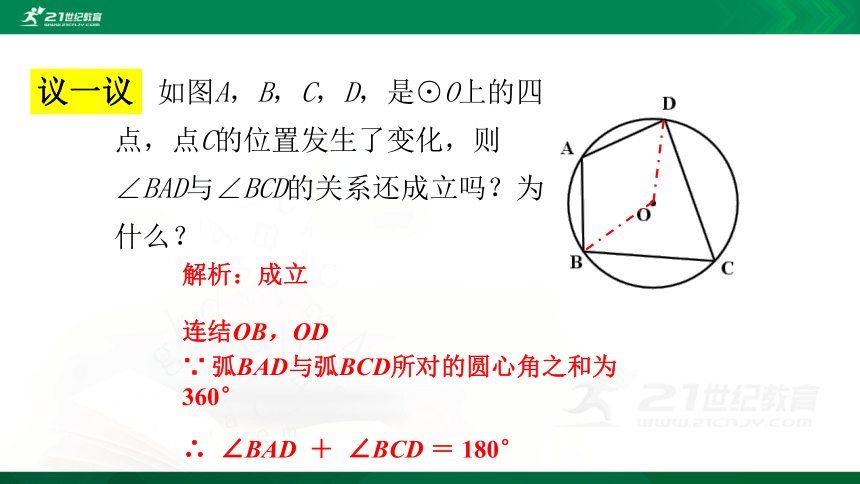
如图A,B,C,D,是⊙O上的四点,点C的位置发生了变化,则∠BAD与∠BCD的关系还成立吗?为什么?
解析:成立
连结OB,OD
∵ 弧BAD与弧BCD所对的圆心角之和为360°
∴ ∠BAD + ∠BCD = 180°
议一议
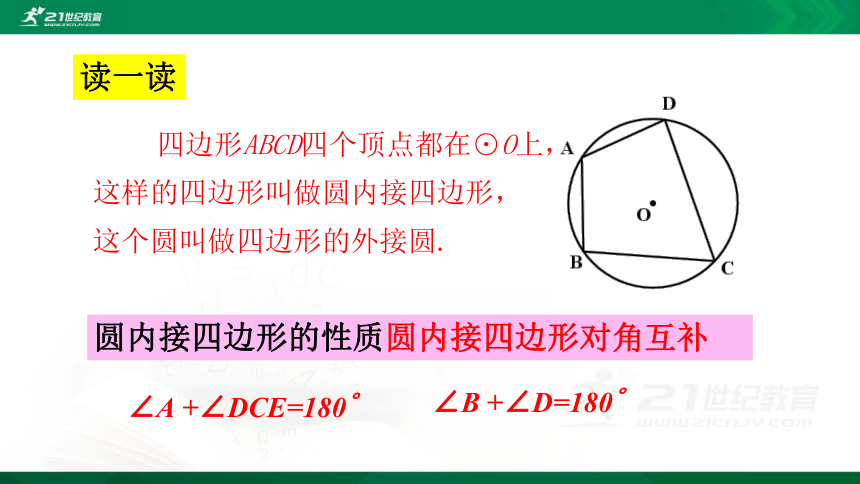
四边形ABCD四个顶点都在⊙O上,
这样的四边形叫做圆内接四边形,
这个圆叫做四边形的外接圆.
读一读
圆内接四边形的性质圆内接四边形对角互补
∠A +∠DCE=180?
∠B +∠D=180?
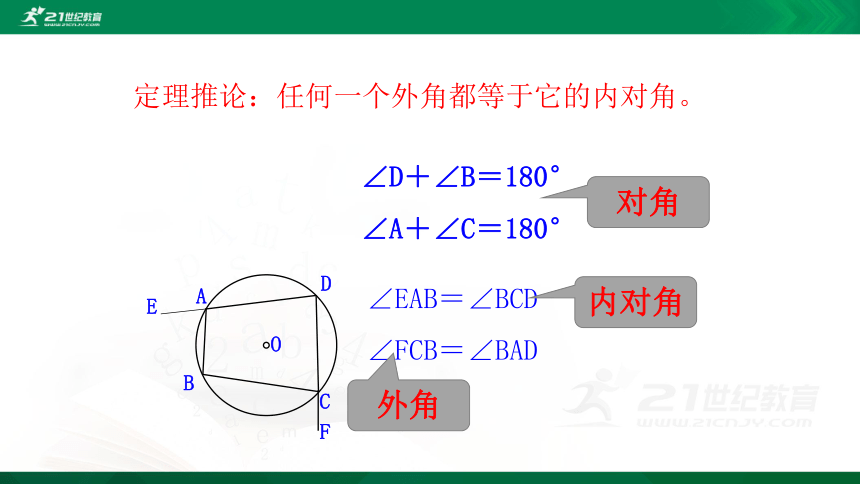
定理推论:任何一个外角都等于它的内对角。
C
B
A
D
O
E
F
∠D+∠B=180°
∠A+∠C=180°
∠EAB=∠BCD
∠FCB=∠BAD
对角
外角
内对角
F
E
D
C
B
A
O
2
O
1
例:如图,⊙O1和⊙O2都经过A、B两点,经过A点的直线CD与⊙O1交于点C,与⊙O2交于点D,经过B点的直线EF与⊙O1交于点E,与⊙O2交于点F。求证:CE∥DF
有两个圆的题目常用的一种辅助线:作公共弦。
此图形是一个考试热门图形。
证明:连接AB,
∠C=∠ABF,
∠ABF+∠D=180? ,
∴∠C+∠D=180? ,
∴CE∥DF
1.如图,已知⊙O的直径AB垂直弦CD于点E,连接CO并延长交AD于点F.若CF⊥AD,AB=2,求CD的长.
练一练
2.如图①,△ABC内接于⊙O,且∠ABC=∠C,点D在弧BC上运动,过点D作DE∥BC,DE交直线AB于点E,连结BD.
(1)证明:∵DE∥BC,∴∠ABC=∠E,∵∠ADB、∠C都是
所对的圆周角,∴∠ADB=∠C,
(1)求证:∠ADB=∠E;
又∠ABC=∠C,∴∠ADB=∠E;
(2)求证:AD2=AC·AE;
2.如图①,△ABC内接于⊙O,且∠ABC=∠C,点D在弧BC上运动,过点D作DE∥BC,DE交直线AB于点E,连结BD.
(3)当点D运动到什么位置时,△DBE∽△ADE?请你利用图②进行探索和证明.
(3)解:点D运动到弧BC中点时,△DBE∽△ADE.证明:∵DE∥BC,∴∠EDB=∠DBC,又∠DBC所对的是弧DC,∠EAD所对的是弧DB,D是弧BC的中点,∴∠DBC=∠EAD,∴∠EDB=∠EAD,又∠DEB=∠AED,∴△DBE∽△ADE.
1.要理解好圆周角定理的推论.
2.构造直径所对的圆周角是圆中的常用方法.引辅助线的方法:
(1)构造直径上的圆周角.
(2)构造同弧所对的圆周角.
3.要多观察图形,善于识别圆周角与圆心角,构造同弧所对的圆周角也是常用方法之一.
课堂小结
2.如图,AB是⊙O的直径,∠C=15°,求∠BAD的度数。
A
B
C
O
D
解:连接BC
∵AB为直径 ∴∠BCA=90°
(直径所对的圆周角为直角)
∴∠BCD+∠DCA=90°,∠ACD=15°
∴∠BCD=90°-15=75°
∴∠BAD=∠BCD=75°(同弧所对的圆周角相等)
方法一:
习题答案
2.如图,AB是⊙O的直径,∠C=15°,求∠BAD的度数。
A
B
C
O
D
解:连接OD
∵∠ACD=15°
∴∠AOD=2∠ACD =30°
(圆周角的度数等于它所对弧上的圆心角的度数的一半)
∵OA=OD
∴∠OAD=∠ODA
又∵∠AOD+∠OAD+∠ODA=180°
∴∠BAD=75°
方法二:
3.如图,分别延长圆内接四边形ABCD的两组对边相交于点E,F,若∠E =40°,∠F =60°,求∠A的度数。
A
B
D
O
C
E
F
解:∵四边形ABCD是圆内接四边形∴∠ADC+∠CBA=180°
(圆内接四边形的对角互补)
∵∠EDC+∠ADC=180°,
∠EBF+∠ABE=180°
∴∠EDC+ ∠EBF=180°
∵∠EDC=∠F+∠A,
∠EBF=∠E+∠A
∴∠F+∠A+∠E+∠A=180°
∵∠E =40°,∠F =60° ∴∠A=40°
1
2
3
4
.
.
O1
O2
A
B
.
C
P
.
C
P
大小不变的角有:
∠ACB ∠APB
∠BCP ∠CBP
课后作业
1.如图,0A,0B是☉0的半径且0A⊥0B,作0A的垂直平分线交☉0于点C,D,连接CB,AB.求证:∠ABC=2∠CBO.
证明:连接0C,AC.∵CD垂直平分OA,
∴0C=AC,∴0C=AC= OA ,
∴△OAC是等边三角形,
∴∠AOC= 60°.∴∠ABC= ∠A0C=30°.
2.如图,四边形ABCD内接于☉0,点E在对角线AC上,EC=BC=DC.(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1 =∠2.
3.如图,已知△ABC内接于☉0,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF// BD.
(1)求证:BE = CE;(2)试判断四边形BFCD的形状,并说明理由;(3)若BC=8,AD=10,求CD的长.
(1)证明: 易证Rt△ABD≌Rt△ACD,∴∠BAD=∠CAD,
∵AB=AC,∴ BE= CE;
(2)解:四边形BFCD是菱形.
理由:由(1)可知AD是BE的垂直平分线∴BF=CF,BD=CD.
在△BED和△CEF中∠FCE=LDBE,BE=CE,∠BED=∠CEF =90°,
∴CF = BD,∴BF=CF=BD=CD∴四边形BFCD是菱形;
(三线合一)
∴△BED≌△CEF,
3.如图,已知△ABC内接于☉0,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF// BD.
(1)求证:BE = CE;(2)试判断四边形BFCD的形状,并说明理由;(3)若BC=8,AD=10,求CD的长.
4.正方形ABCD内接于☉0,如图所示,在劣弧AB_上取一点E,连接DE, BE,过点D作DF//BE交☉0于点F,连接BF,AF,且AF与DE相交于点G,求证:(1)四边形EBFD是矩形;(2 )DG = BE.
4.正方形ABCD内接于☉0,如图所示,在劣弧AB_上取一点E,连接DE, BE,过点D作DF//BE交☉0于点F,连接BF,AF,且AF与DE相交于点G,求证:(1)四边形EBFD是矩形;(2 )DG = BE.
5.如图,AB是半圆的直径,∠ABC的平分线交半圆于点D,AD和BC的延长线交于圆外一点E,连接CD.(1)求证:△EDC是等腰三角形;
(2)若AB=5,BC=3,求四边形ABCD的面积.
(1)证明∵AB是半圆的直径,
∴∠ADB =∠ACB =90°.
∵∠ABC的平分线交半圆于点D,
∴BA=BE,AD=ED,
∴CD为RT?ACE斜边上的中线,
5.如图,AB是半圆的直径,∠ABC的平分线交半圆于点D,AD和BC的延长线交于圆外一点E,连接CD.(1)求证:△EDC是等腰三角形;
(2)若AB=5,BC=3,求四边形ABCD的面积.
6.如图,在Rt△ABC中,∠ABC =90°,点M是AC的中点,以AB为直径作☉0分别交AC,BM于点D,E.(1)求证:MD=ME;(2)填空:①若AB=6,当AD=2DM时,DE= ( ) ;②连接OD,OE,当∠A的度数为( )时, 四边形ODME是菱形.
60°
2
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
九年级
3.4圆周角和圆心角的关系第2课时
1.圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角.
2.圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半.
同弧(等弧)所对的圆周角相等.
3.圆周角定理推论:
相等的圆周角所对的弧相等.
4.在同圆或等圆中,
相等的弦所对的弧不一定相等.(优劣弧的区别)
5.在同圆或等圆中,
●O
B
A
C
D
E
复习巩固
B
C
●O
A
┗
圆周角定理的推论
用于判断某条弦是否是直径
用于构造直角
半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径.
●O
D
A
B
C
例1.如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到C,使AC=AB,BD与CD的大小有什么关系?为什么?
解析:BD=CD;
理由:如图,连接AD.
∵AB是⊙O的直径,∴∠ADB=90°,
即AD⊥BC.
又∵AC=AB,∴BD=CD.
例2 如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长.
又在Rt△ABD中,AD2+BD2=AB2,
·
A
B
C
D
O
解:∵AB是直径,
∴ ∠ACB= ∠ADB=90°.
在Rt△ABC中,
∵CD平分∠ACB,
∴AD=BD.
如图A,B,C,D,是⊙O上的四点,AC为⊙O的直径,则∠BAD与∠BCD之间有什么关系?为什么?
解析:∵AC是⊙O的直径,
∴∠ADB=90° ∠ABC=90°
∴ ∠BAD+ ∠BCD
=360°-90° -90° = 180°
议一议
如图A,B,C,D,是⊙O上的四点,点C的位置发生了变化,则∠BAD与∠BCD的关系还成立吗?为什么?
解析:成立
连结OB,OD
∵ 弧BAD与弧BCD所对的圆心角之和为360°
∴ ∠BAD + ∠BCD = 180°
议一议
四边形ABCD四个顶点都在⊙O上,
这样的四边形叫做圆内接四边形,
这个圆叫做四边形的外接圆.
读一读
圆内接四边形的性质圆内接四边形对角互补
∠A +∠DCE=180?
∠B +∠D=180?
定理推论:任何一个外角都等于它的内对角。
C
B
A
D
O
E
F
∠D+∠B=180°
∠A+∠C=180°
∠EAB=∠BCD
∠FCB=∠BAD
对角
外角
内对角
F
E
D
C
B
A
O
2
O
1
例:如图,⊙O1和⊙O2都经过A、B两点,经过A点的直线CD与⊙O1交于点C,与⊙O2交于点D,经过B点的直线EF与⊙O1交于点E,与⊙O2交于点F。求证:CE∥DF
有两个圆的题目常用的一种辅助线:作公共弦。
此图形是一个考试热门图形。
证明:连接AB,
∠C=∠ABF,
∠ABF+∠D=180? ,
∴∠C+∠D=180? ,
∴CE∥DF
1.如图,已知⊙O的直径AB垂直弦CD于点E,连接CO并延长交AD于点F.若CF⊥AD,AB=2,求CD的长.
练一练
2.如图①,△ABC内接于⊙O,且∠ABC=∠C,点D在弧BC上运动,过点D作DE∥BC,DE交直线AB于点E,连结BD.
(1)证明:∵DE∥BC,∴∠ABC=∠E,∵∠ADB、∠C都是
所对的圆周角,∴∠ADB=∠C,
(1)求证:∠ADB=∠E;
又∠ABC=∠C,∴∠ADB=∠E;
(2)求证:AD2=AC·AE;
2.如图①,△ABC内接于⊙O,且∠ABC=∠C,点D在弧BC上运动,过点D作DE∥BC,DE交直线AB于点E,连结BD.
(3)当点D运动到什么位置时,△DBE∽△ADE?请你利用图②进行探索和证明.
(3)解:点D运动到弧BC中点时,△DBE∽△ADE.证明:∵DE∥BC,∴∠EDB=∠DBC,又∠DBC所对的是弧DC,∠EAD所对的是弧DB,D是弧BC的中点,∴∠DBC=∠EAD,∴∠EDB=∠EAD,又∠DEB=∠AED,∴△DBE∽△ADE.
1.要理解好圆周角定理的推论.
2.构造直径所对的圆周角是圆中的常用方法.引辅助线的方法:
(1)构造直径上的圆周角.
(2)构造同弧所对的圆周角.
3.要多观察图形,善于识别圆周角与圆心角,构造同弧所对的圆周角也是常用方法之一.
课堂小结
2.如图,AB是⊙O的直径,∠C=15°,求∠BAD的度数。
A
B
C
O
D
解:连接BC
∵AB为直径 ∴∠BCA=90°
(直径所对的圆周角为直角)
∴∠BCD+∠DCA=90°,∠ACD=15°
∴∠BCD=90°-15=75°
∴∠BAD=∠BCD=75°(同弧所对的圆周角相等)
方法一:
习题答案
2.如图,AB是⊙O的直径,∠C=15°,求∠BAD的度数。
A
B
C
O
D
解:连接OD
∵∠ACD=15°
∴∠AOD=2∠ACD =30°
(圆周角的度数等于它所对弧上的圆心角的度数的一半)
∵OA=OD
∴∠OAD=∠ODA
又∵∠AOD+∠OAD+∠ODA=180°
∴∠BAD=75°
方法二:
3.如图,分别延长圆内接四边形ABCD的两组对边相交于点E,F,若∠E =40°,∠F =60°,求∠A的度数。
A
B
D
O
C
E
F
解:∵四边形ABCD是圆内接四边形∴∠ADC+∠CBA=180°
(圆内接四边形的对角互补)
∵∠EDC+∠ADC=180°,
∠EBF+∠ABE=180°
∴∠EDC+ ∠EBF=180°
∵∠EDC=∠F+∠A,
∠EBF=∠E+∠A
∴∠F+∠A+∠E+∠A=180°
∵∠E =40°,∠F =60° ∴∠A=40°
1
2
3
4
.
.
O1
O2
A
B
.
C
P
.
C
P
大小不变的角有:
∠ACB ∠APB
∠BCP ∠CBP
课后作业
1.如图,0A,0B是☉0的半径且0A⊥0B,作0A的垂直平分线交☉0于点C,D,连接CB,AB.求证:∠ABC=2∠CBO.
证明:连接0C,AC.∵CD垂直平分OA,
∴0C=AC,∴0C=AC= OA ,
∴△OAC是等边三角形,
∴∠AOC= 60°.∴∠ABC= ∠A0C=30°.
2.如图,四边形ABCD内接于☉0,点E在对角线AC上,EC=BC=DC.(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1 =∠2.
3.如图,已知△ABC内接于☉0,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF// BD.
(1)求证:BE = CE;(2)试判断四边形BFCD的形状,并说明理由;(3)若BC=8,AD=10,求CD的长.
(1)证明: 易证Rt△ABD≌Rt△ACD,∴∠BAD=∠CAD,
∵AB=AC,∴ BE= CE;
(2)解:四边形BFCD是菱形.
理由:由(1)可知AD是BE的垂直平分线∴BF=CF,BD=CD.
在△BED和△CEF中∠FCE=LDBE,BE=CE,∠BED=∠CEF =90°,
∴CF = BD,∴BF=CF=BD=CD∴四边形BFCD是菱形;
(三线合一)
∴△BED≌△CEF,
3.如图,已知△ABC内接于☉0,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF// BD.
(1)求证:BE = CE;(2)试判断四边形BFCD的形状,并说明理由;(3)若BC=8,AD=10,求CD的长.
4.正方形ABCD内接于☉0,如图所示,在劣弧AB_上取一点E,连接DE, BE,过点D作DF//BE交☉0于点F,连接BF,AF,且AF与DE相交于点G,求证:(1)四边形EBFD是矩形;(2 )DG = BE.
4.正方形ABCD内接于☉0,如图所示,在劣弧AB_上取一点E,连接DE, BE,过点D作DF//BE交☉0于点F,连接BF,AF,且AF与DE相交于点G,求证:(1)四边形EBFD是矩形;(2 )DG = BE.
5.如图,AB是半圆的直径,∠ABC的平分线交半圆于点D,AD和BC的延长线交于圆外一点E,连接CD.(1)求证:△EDC是等腰三角形;
(2)若AB=5,BC=3,求四边形ABCD的面积.
(1)证明∵AB是半圆的直径,
∴∠ADB =∠ACB =90°.
∵∠ABC的平分线交半圆于点D,
∴BA=BE,AD=ED,
∴CD为RT?ACE斜边上的中线,
5.如图,AB是半圆的直径,∠ABC的平分线交半圆于点D,AD和BC的延长线交于圆外一点E,连接CD.(1)求证:△EDC是等腰三角形;
(2)若AB=5,BC=3,求四边形ABCD的面积.
6.如图,在Rt△ABC中,∠ABC =90°,点M是AC的中点,以AB为直径作☉0分别交AC,BM于点D,E.(1)求证:MD=ME;(2)填空:①若AB=6,当AD=2DM时,DE= ( ) ;②连接OD,OE,当∠A的度数为( )时, 四边形ODME是菱形.
60°
2
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
