3.5 确定圆的条件 课件(共27张PPT)
文档属性
| 名称 | 3.5 确定圆的条件 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-28 00:00:00 | ||
图片预览


文档简介
数学北师大版
九年级
3.5 确定圆的条件
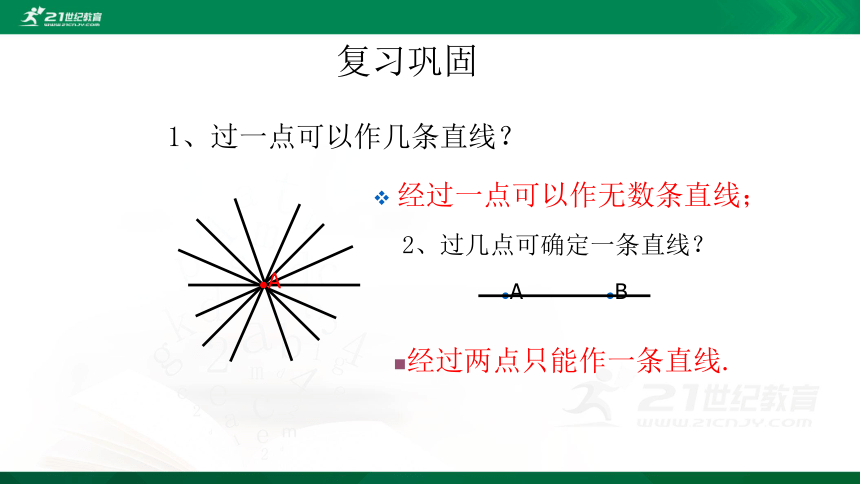
1、过一点可以作几条直线?
经过一点可以作无数条直线;
●A
2、过几点可确定一条直线?
经过两点只能作一条直线.
●A
●B
复习巩固
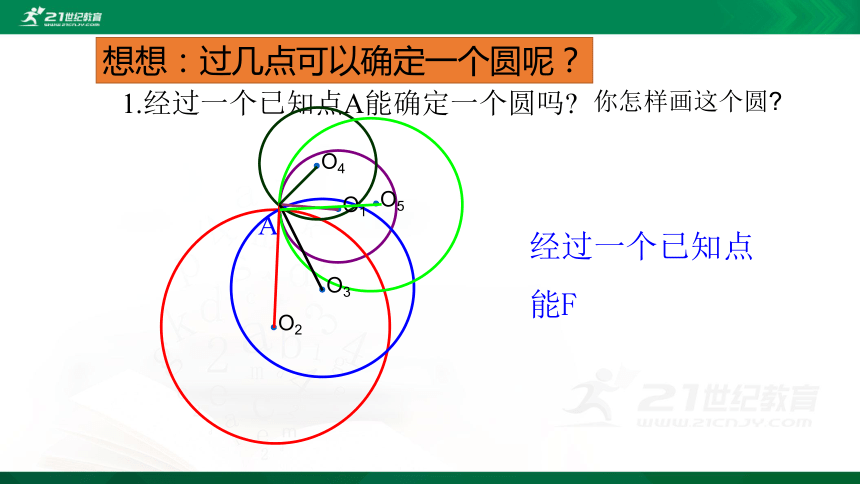
1.经过一个已知点A能确定一个圆吗?
A
你怎样画这个圆?
●O1
●O2
●O3
●O5
●O4
想想:过几点可以确定一个圆呢?
经过一个已知点
能F
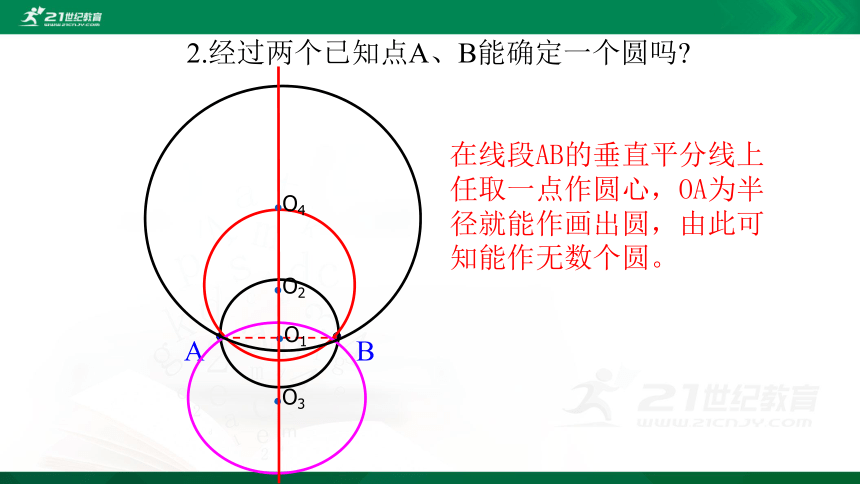
2.经过两个已知点A、B能确定一个圆吗?
A
B
在线段AB的垂直平分线上任取一点作圆心,OA为半径就能作画出圆,由此可知能作无数个圆。
●O1
●O2
●O3
●O4
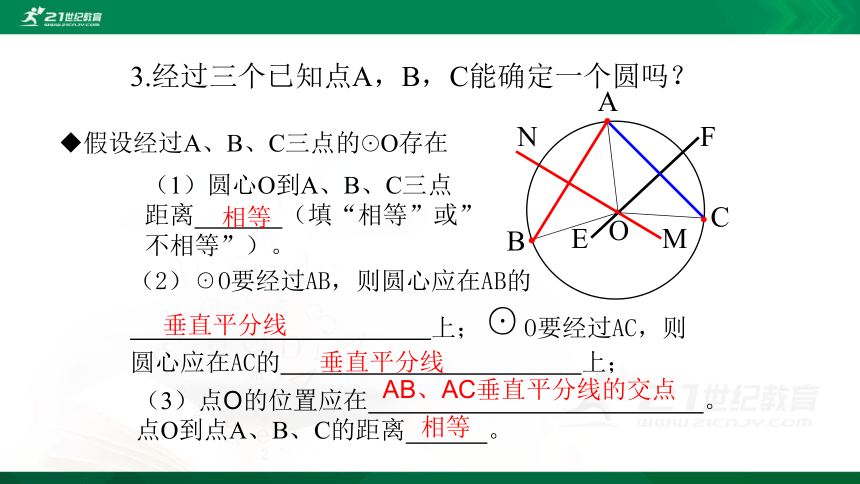
3.经过三个已知点A,B,C能确定一个圆吗?
假设经过A、B、C三点的☉O存在
(1)圆心O到A、B、C三点距离 (填“相等”或”不相等”)。
(2)☉O要经过AB,则圆心应在AB的
上;☉O要经过AC,则圆心应在AC的 上;
(3)点O的位置应在 。点O到点A、B、C的距离 。
N
M
F
E
O
A
B
C
相等
垂直平分线
垂直平分线
相等
AB、AC垂直平分线的交点
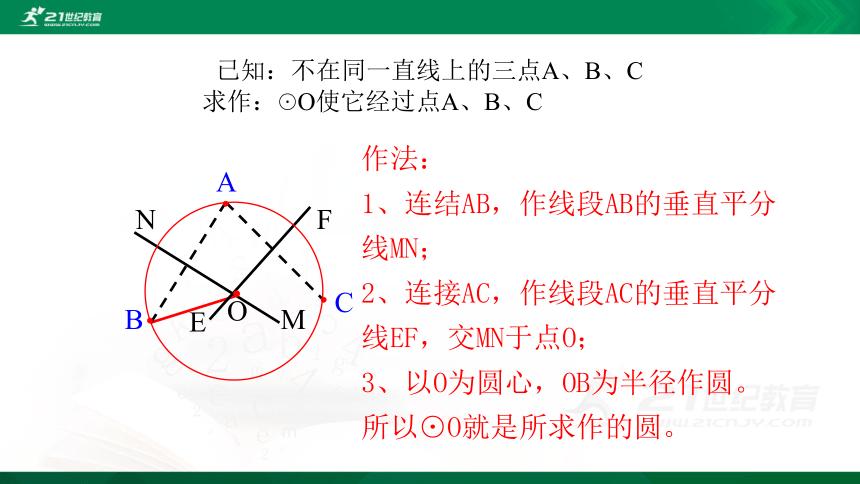
已知:不在同一直线上的三点A、B、C
求作:☉O使它经过点A、B、C
作法:
1、连结AB,作线段AB的垂直平分线MN;
2、连接AC,作线段AC的垂直平分线EF,交MN于点O;
3、以O为圆心,OB为半径作圆。
所以⊙O就是所求作的圆。
O
N
M
F
E
A
B
C
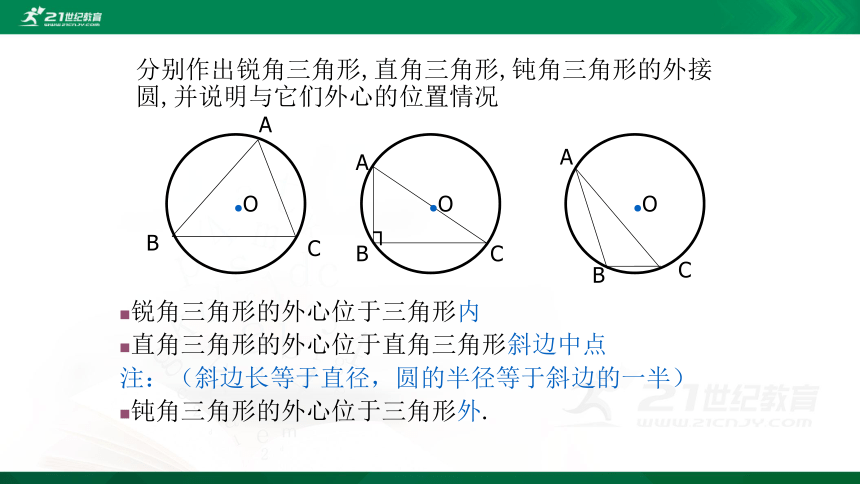
分别作出锐角三角形,直角三角形,钝角三角形的外接圆,并说明与它们外心的位置情况
锐角三角形的外心位于三角形内
直角三角形的外心位于直角三角形斜边中点
注:(斜边长等于直径,圆的半径等于斜边的一半)
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
A
B
C
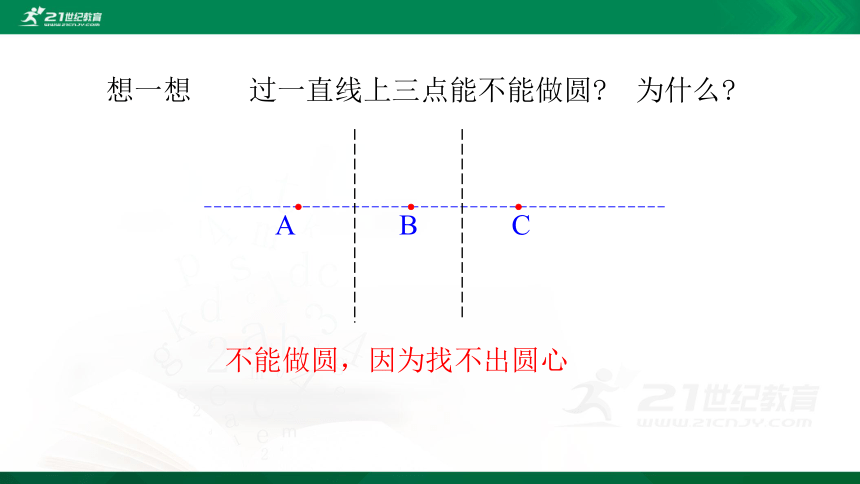
过一直线上三点能不能做圆? 为什么?
想一想
不能做圆,因为找不出圆心
定理:
不在同一直线上的三点确定一个圆
经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形。
如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心
外心是△ABC三条边的垂直平分线的交点,
它到三角形的三个顶点的距离相等。
C
A
B
O
例:如何将一个如图所示的破损的圆盘复原?
方法:1、在圆弧上任取三点A、B、C。
2、作线段AB、BC的垂直平分线,其交点O即为圆心。
3、以点O为圆心,OC长为半径作圆。
☉O即为所求。
A
B
C
O
1.下列命题错误的有( )
①经过三点一定可以作圆;②三角形的外心到三角形各顶点的距离相等;③平行四边形的四个顶点在同一个圆上;④任意一个三角形一定有一个外接圆,且只有一个外接圆.
A.①③④ B.①②③
C.①③ D.②④
C
练习
2.如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,下列叙述正确的是( )
A.O是△AEB的外心,O是△AED的外心
B.O是△AEB的外心,O不是△AED的外心
C.O不是△AEB的外心,O是△AED的外心
D.O不是△AEB的外心,O不是△AED的外心
B
C
4.如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E.
(1)求证:DE=DB;
(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.
4.如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E.
(1)求证:DE=DB;
(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.
本课小结
经过一点可以作无数个圆。
经过两点可以作无数个圆,圆心在这两点连线的垂直平分线上。
不在同一直线上的三点确定一个圆。
三角形有且只有一个外接圆,外接圆的圆心是三边垂直平分线的交点。
课后作业
1.如图,AD为△ABC的外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
(1)求证:BD=CD;
(2)请判断B,E,C三点是否在以点D为圆心,以DB为半径的圆上?并说明理由.
(1) 证明:∵AD为直径,AD⊥BC,∴由垂径定理,得
(2)B,E,C三点在以点D为圆心,以DB为半径的圆上.
理由如下:由(1)知,
1.如图,AD为△ABC的外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
(1)求证:BD=CD;
(2)请判断B,E,C三点是否在以点D为圆心,以DB为半径的圆上?并说明理由.
2.如图,⊙O是△ABC的外接圆,AB=AC,点D在边BC上,AE∥BC,AE=BD. (1)求证:AD=CE; (2)如果点G在线段DC上(不与点D重合),且AG=AD,求证:四边形AGCE是平行四边形.
2.如图,⊙O是△ABC的外接圆,AB=AC,点D在边BC上,AE∥BC,AE=BD. (1)求证:AD=CE; (2)如果点G在线段DC上(不与点D重合),且AG=AD,求证:四边形AGCE是平行四边形.
3.如图,△ABC内接于☉0,AH⊥BC于点H.若AC=24,AH=18,☉0的半径OC=13,求AB长。
×
×
4
5.如图,D是△ABC的边BC的中点,过AD延长线上的点E作AD的垂线EF,E为垂足,EF与AB的延长线相交于点F,点O在AD上,AO=CO,BC// EF.求证:(1)AB= AC;(2)点O为△ABC的外心.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
九年级
3.5 确定圆的条件
1、过一点可以作几条直线?
经过一点可以作无数条直线;
●A
2、过几点可确定一条直线?
经过两点只能作一条直线.
●A
●B
复习巩固
1.经过一个已知点A能确定一个圆吗?
A
你怎样画这个圆?
●O1
●O2
●O3
●O5
●O4
想想:过几点可以确定一个圆呢?
经过一个已知点
能F
2.经过两个已知点A、B能确定一个圆吗?
A
B
在线段AB的垂直平分线上任取一点作圆心,OA为半径就能作画出圆,由此可知能作无数个圆。
●O1
●O2
●O3
●O4
3.经过三个已知点A,B,C能确定一个圆吗?
假设经过A、B、C三点的☉O存在
(1)圆心O到A、B、C三点距离 (填“相等”或”不相等”)。
(2)☉O要经过AB,则圆心应在AB的
上;☉O要经过AC,则圆心应在AC的 上;
(3)点O的位置应在 。点O到点A、B、C的距离 。
N
M
F
E
O
A
B
C
相等
垂直平分线
垂直平分线
相等
AB、AC垂直平分线的交点
已知:不在同一直线上的三点A、B、C
求作:☉O使它经过点A、B、C
作法:
1、连结AB,作线段AB的垂直平分线MN;
2、连接AC,作线段AC的垂直平分线EF,交MN于点O;
3、以O为圆心,OB为半径作圆。
所以⊙O就是所求作的圆。
O
N
M
F
E
A
B
C
分别作出锐角三角形,直角三角形,钝角三角形的外接圆,并说明与它们外心的位置情况
锐角三角形的外心位于三角形内
直角三角形的外心位于直角三角形斜边中点
注:(斜边长等于直径,圆的半径等于斜边的一半)
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
A
B
C
过一直线上三点能不能做圆? 为什么?
想一想
不能做圆,因为找不出圆心
定理:
不在同一直线上的三点确定一个圆
经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形。
如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心
外心是△ABC三条边的垂直平分线的交点,
它到三角形的三个顶点的距离相等。
C
A
B
O
例:如何将一个如图所示的破损的圆盘复原?
方法:1、在圆弧上任取三点A、B、C。
2、作线段AB、BC的垂直平分线,其交点O即为圆心。
3、以点O为圆心,OC长为半径作圆。
☉O即为所求。
A
B
C
O
1.下列命题错误的有( )
①经过三点一定可以作圆;②三角形的外心到三角形各顶点的距离相等;③平行四边形的四个顶点在同一个圆上;④任意一个三角形一定有一个外接圆,且只有一个外接圆.
A.①③④ B.①②③
C.①③ D.②④
C
练习
2.如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,下列叙述正确的是( )
A.O是△AEB的外心,O是△AED的外心
B.O是△AEB的外心,O不是△AED的外心
C.O不是△AEB的外心,O是△AED的外心
D.O不是△AEB的外心,O不是△AED的外心
B
C
4.如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E.
(1)求证:DE=DB;
(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.
4.如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E.
(1)求证:DE=DB;
(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.
本课小结
经过一点可以作无数个圆。
经过两点可以作无数个圆,圆心在这两点连线的垂直平分线上。
不在同一直线上的三点确定一个圆。
三角形有且只有一个外接圆,外接圆的圆心是三边垂直平分线的交点。
课后作业
1.如图,AD为△ABC的外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
(1)求证:BD=CD;
(2)请判断B,E,C三点是否在以点D为圆心,以DB为半径的圆上?并说明理由.
(1) 证明:∵AD为直径,AD⊥BC,∴由垂径定理,得
(2)B,E,C三点在以点D为圆心,以DB为半径的圆上.
理由如下:由(1)知,
1.如图,AD为△ABC的外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
(1)求证:BD=CD;
(2)请判断B,E,C三点是否在以点D为圆心,以DB为半径的圆上?并说明理由.
2.如图,⊙O是△ABC的外接圆,AB=AC,点D在边BC上,AE∥BC,AE=BD. (1)求证:AD=CE; (2)如果点G在线段DC上(不与点D重合),且AG=AD,求证:四边形AGCE是平行四边形.
2.如图,⊙O是△ABC的外接圆,AB=AC,点D在边BC上,AE∥BC,AE=BD. (1)求证:AD=CE; (2)如果点G在线段DC上(不与点D重合),且AG=AD,求证:四边形AGCE是平行四边形.
3.如图,△ABC内接于☉0,AH⊥BC于点H.若AC=24,AH=18,☉0的半径OC=13,求AB长。
×
×
4
5.如图,D是△ABC的边BC的中点,过AD延长线上的点E作AD的垂线EF,E为垂足,EF与AB的延长线相交于点F,点O在AD上,AO=CO,BC// EF.求证:(1)AB= AC;(2)点O为△ABC的外心.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
