3.6 直线和圆的位置关系(第1课时) 课件(共19张PPT)
文档属性
| 名称 | 3.6 直线和圆的位置关系(第1课时) 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-28 00:00:00 | ||
图片预览





文档简介
数学北师大版
九年级
第三章 圆
3.6 直线和圆的位置关系第1课时
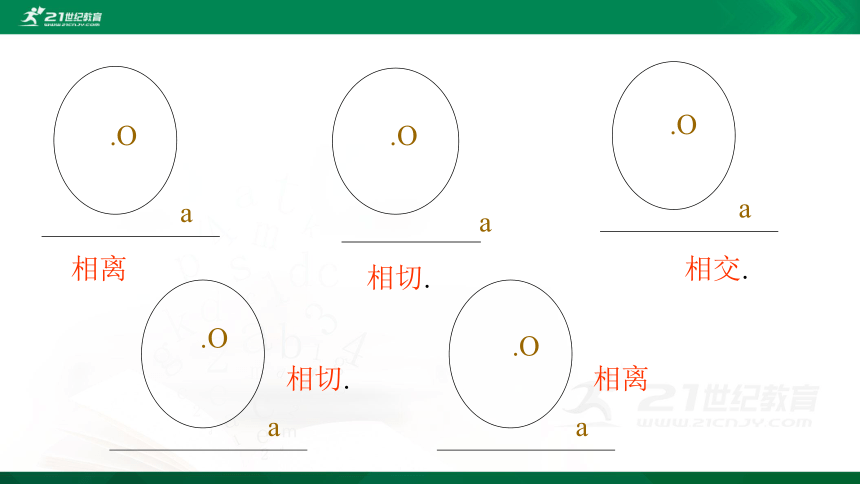
a
.O
a
.O
a
.O
a
.O
a
.O
相离
相切.
相切.
相离
相交.
a
.O
图 1
b
.A
.O
图 2
c
.
F
.E
.O
图 3
这时直线叫做圆的割线 ,
公共点叫直线与圆的交点。
直线与圆没有公共点时,叫做直线与圆相离.
直线与圆有唯一公共点时,叫做直线与圆相切.
直线与圆有两个公共点时,叫做直线与圆相交.
这时直线叫做圆的切线,
唯一公共点叫做直线与圆的切点。
1.直线与圆的位置关系 (图形特征)
地平线
你发现这个自然现象反映出直线和圆的公共点的个数有 种情况。
三种
如果我们把太阳看成一个圆,地平线看成一条直线,那你能根据直线与圆的公共点的个数想象一下,直线和圆的位置关系有几种?
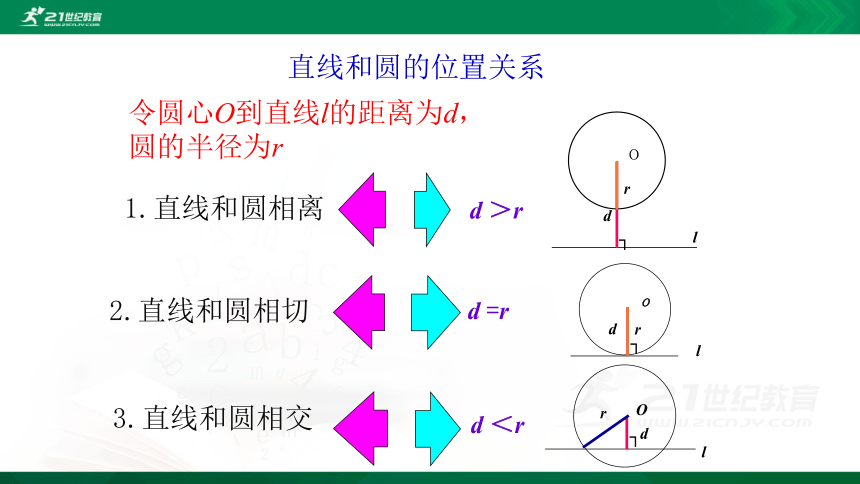
O
l
┐
d
r
o
l
2.直线和圆相切
┐
d
r
d =r
O
l
3.直线和圆相交
d <r
d
┐
r
1.直线和圆相离
d >r
直线和圆的位置关系
令圆心O到直线l的距离为d,圆的半径为r
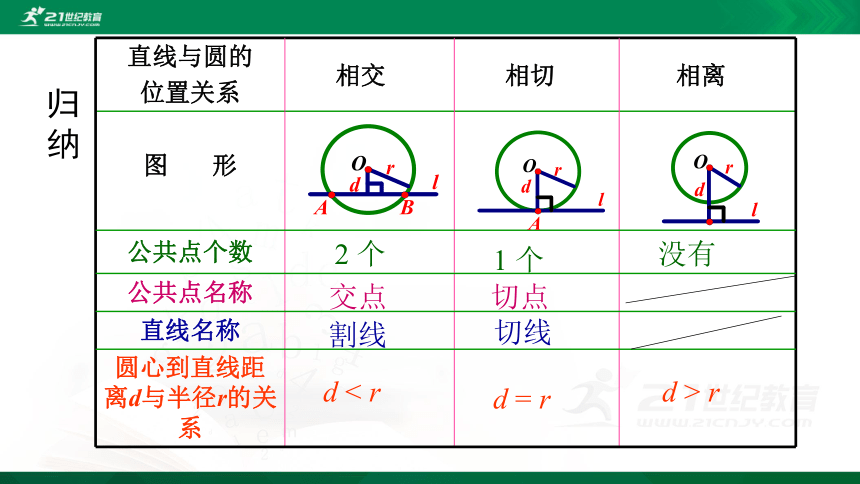
归 纳
直线与圆的
位置关系
相交
相切
相离
图 形
公共点个数
公共点名称
直线名称
圆心到直线距离d与半径r的关系
2 个
交点
割线
1 个
切点
切线
d < r
d = r
d > r
没有
o
l
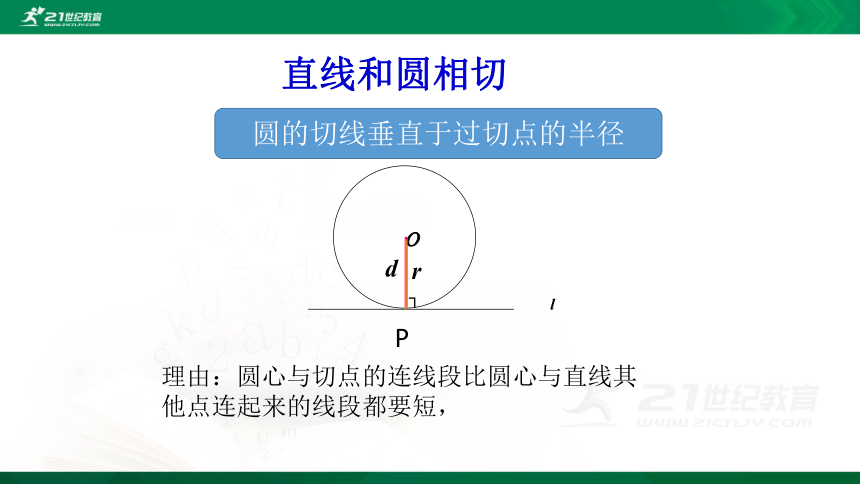
直线和圆相切
┐
d
r
圆的切线垂直于过切点的半径
P
理由:圆心与切点的连线段比圆心与直线其他点连起来的线段都要短,
例1.已知Rt△ABC的斜边AB=8cm,AC=4cm.
(1)以点C为圆心作圆,当半径为多长时,AB与☉C相切?
(2)以点C为圆心,分别以2cm和4cm的长为半径作两个圆,这两个圆与AB分别有怎样的位置关系?
B
A
C
解:(1)过点C作CD⊥AB于点D.
∵AB=8cm,AC=4cm.
∴∠A=60°.
D
(2)由(1)可知,圆心到AB的距离d= cm,所以
当r=2cm时,d>r,AB与☉C相离;
当r=4cm时,d即圆心C到AB的距离d=2.4cm。
(1)当r=2cm时, ∵d>r,∴⊙C与AB相离。
(2)当r=2.4cm时,∵d=r,∴⊙C与AB相切。
(3)当r=3cm时, ∵d<r,∴⊙C与AB相交。
解:过C作CD⊥AB,垂足为D。
在Rt△ABC中,
AB= =
=5(cm)
根据三角形面积公式有
CD·AB=AC·BC
∴CD= =
=2.4(cm)。
B
C
A
D
5
3
例2Rt△ABC,∠C=90°AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?(1)r=2cm;
(2)r=2.4cm (3)r=3cm。
4
2.识别直线与圆的位置关系的方法:
(1)一种是根据定义进行识别:
直线l与⊙O没有公共点 直线l与⊙O相离.
直线l与⊙O只有一个公共点 直线l与⊙O相切.
直线l与⊙O有两个公共点 直线l与⊙O相交.
(2)另一种是根据圆心到直线的距离d与圆半径r的大小关系来进行识别:
d >r 直线l与⊙O相离;
d =r 直线l与⊙O相切;
d1.直线与圆的位置关系三种:相离、相切和相交.
本节小结
课后作业
1.如图所示,半径为2的☉P的圆心在直线y=2x- 1上运动.(1)当☉P和x轴相切时,写出点P的坐标;(2)当☉P和y轴相切时,写出点P的坐标;(3)☉P是否能同时与x轴和y轴相切?若能,写出点P的坐标;若不能,说明理由.
2.已知☉O的半径r =7cm,直线l1 // l2,且l1与⊙O相切,圆心O到l2的距离为9cm.求l1与l2的距离.
o
l1
l2
A
B
C
l2
(1) l2与l1在圆的同一侧:
m=9-7=2 cm
(2)l2与l1在圆的两侧:
m=9+7=16 cm
解:设 l2与l1的距离为m,
3.如图,AB是☉0的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,射线EP交AC弧于点F,交过点C的切线于点D.(1)求证:DC= DP;(2)若∠CAB =30°,当F是AC弧的中点时,判断以A,0,C,F为顶点的四边形是什么特殊四边形?说明理由.
3.如图,AB是☉0的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,射线EP交AC弧于点F,交过点C的切线于点D.(1)求证:DC= DP;(2)若∠CAB =30°,当F是AC弧的中点时,判断以A,0,C,F为顶点的四边形是什么特殊四边形?说明理由.
4.如图,AD是☉0的直径,AB为☉0的弦,OP⊥AD,OP与AB的延长线交于点P,过B点的切线交OP于点C.(1)求证:∠CBP=∠ADB;(2)若OA =2,AB=1 ,求线段BP的长.
而0A=OB
(1)证明:连接OB.∵AD是☉0的直径,
∴∠ABD=90°,
∴∠A+∠ADB=90°.
∵BC为切线,
∴OB⊥BC,
∴∠OBC=90°,
∴∠OBA+∠CBP=90°,
∴∠CBP= ∠ADB;
∴∠A=∠0BA,
4.如图,AD是☉0的直径,AB为☉0的弦,OP⊥AD,OP与AB的延长线交于点P,过B点的切线交OP于点C.(1)求证:∠CBP=∠ADB;(2)若OA =2,AB=1 ,求线段BP的长.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
九年级
第三章 圆
3.6 直线和圆的位置关系第1课时
a
.O
a
.O
a
.O
a
.O
a
.O
相离
相切.
相切.
相离
相交.
a
.O
图 1
b
.A
.O
图 2
c
.
F
.E
.O
图 3
这时直线叫做圆的割线 ,
公共点叫直线与圆的交点。
直线与圆没有公共点时,叫做直线与圆相离.
直线与圆有唯一公共点时,叫做直线与圆相切.
直线与圆有两个公共点时,叫做直线与圆相交.
这时直线叫做圆的切线,
唯一公共点叫做直线与圆的切点。
1.直线与圆的位置关系 (图形特征)
地平线
你发现这个自然现象反映出直线和圆的公共点的个数有 种情况。
三种
如果我们把太阳看成一个圆,地平线看成一条直线,那你能根据直线与圆的公共点的个数想象一下,直线和圆的位置关系有几种?
O
l
┐
d
r
o
l
2.直线和圆相切
┐
d
r
d =r
O
l
3.直线和圆相交
d <r
d
┐
r
1.直线和圆相离
d >r
直线和圆的位置关系
令圆心O到直线l的距离为d,圆的半径为r
归 纳
直线与圆的
位置关系
相交
相切
相离
图 形
公共点个数
公共点名称
直线名称
圆心到直线距离d与半径r的关系
2 个
交点
割线
1 个
切点
切线
d < r
d = r
d > r
没有
o
l
直线和圆相切
┐
d
r
圆的切线垂直于过切点的半径
P
理由:圆心与切点的连线段比圆心与直线其他点连起来的线段都要短,
例1.已知Rt△ABC的斜边AB=8cm,AC=4cm.
(1)以点C为圆心作圆,当半径为多长时,AB与☉C相切?
(2)以点C为圆心,分别以2cm和4cm的长为半径作两个圆,这两个圆与AB分别有怎样的位置关系?
B
A
C
解:(1)过点C作CD⊥AB于点D.
∵AB=8cm,AC=4cm.
∴∠A=60°.
D
(2)由(1)可知,圆心到AB的距离d= cm,所以
当r=2cm时,d>r,AB与☉C相离;
当r=4cm时,d
(1)当r=2cm时, ∵d>r,∴⊙C与AB相离。
(2)当r=2.4cm时,∵d=r,∴⊙C与AB相切。
(3)当r=3cm时, ∵d<r,∴⊙C与AB相交。
解:过C作CD⊥AB,垂足为D。
在Rt△ABC中,
AB= =
=5(cm)
根据三角形面积公式有
CD·AB=AC·BC
∴CD= =
=2.4(cm)。
B
C
A
D
5
3
例2Rt△ABC,∠C=90°AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?(1)r=2cm;
(2)r=2.4cm (3)r=3cm。
4
2.识别直线与圆的位置关系的方法:
(1)一种是根据定义进行识别:
直线l与⊙O没有公共点 直线l与⊙O相离.
直线l与⊙O只有一个公共点 直线l与⊙O相切.
直线l与⊙O有两个公共点 直线l与⊙O相交.
(2)另一种是根据圆心到直线的距离d与圆半径r的大小关系来进行识别:
d >r 直线l与⊙O相离;
d =r 直线l与⊙O相切;
d
本节小结
课后作业
1.如图所示,半径为2的☉P的圆心在直线y=2x- 1上运动.(1)当☉P和x轴相切时,写出点P的坐标;(2)当☉P和y轴相切时,写出点P的坐标;(3)☉P是否能同时与x轴和y轴相切?若能,写出点P的坐标;若不能,说明理由.
2.已知☉O的半径r =7cm,直线l1 // l2,且l1与⊙O相切,圆心O到l2的距离为9cm.求l1与l2的距离.
o
l1
l2
A
B
C
l2
(1) l2与l1在圆的同一侧:
m=9-7=2 cm
(2)l2与l1在圆的两侧:
m=9+7=16 cm
解:设 l2与l1的距离为m,
3.如图,AB是☉0的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,射线EP交AC弧于点F,交过点C的切线于点D.(1)求证:DC= DP;(2)若∠CAB =30°,当F是AC弧的中点时,判断以A,0,C,F为顶点的四边形是什么特殊四边形?说明理由.
3.如图,AB是☉0的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,射线EP交AC弧于点F,交过点C的切线于点D.(1)求证:DC= DP;(2)若∠CAB =30°,当F是AC弧的中点时,判断以A,0,C,F为顶点的四边形是什么特殊四边形?说明理由.
4.如图,AD是☉0的直径,AB为☉0的弦,OP⊥AD,OP与AB的延长线交于点P,过B点的切线交OP于点C.(1)求证:∠CBP=∠ADB;(2)若OA =2,AB=1 ,求线段BP的长.
而0A=OB
(1)证明:连接OB.∵AD是☉0的直径,
∴∠ABD=90°,
∴∠A+∠ADB=90°.
∵BC为切线,
∴OB⊥BC,
∴∠OBC=90°,
∴∠OBA+∠CBP=90°,
∴∠CBP= ∠ADB;
∴∠A=∠0BA,
4.如图,AD是☉0的直径,AB为☉0的弦,OP⊥AD,OP与AB的延长线交于点P,过B点的切线交OP于点C.(1)求证:∠CBP=∠ADB;(2)若OA =2,AB=1 ,求线段BP的长.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
